鲁教版(五四制)数学七年级下册 8.6 三角形外角定理(2) 课件(共14张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学七年级下册 8.6 三角形外角定理(2) 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 234.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-18 05:34:58 | ||
图片预览


文档简介
(共14张PPT)
三角形外角定理
1.能够灵活运用三角形内角和定理及两个推论解决问题。
2.经历从不同角度寻求分析问题和解决问题的过程,体验解决问题方法的多样性
3.养成独立思考、合作交流的学习习惯
学习目标
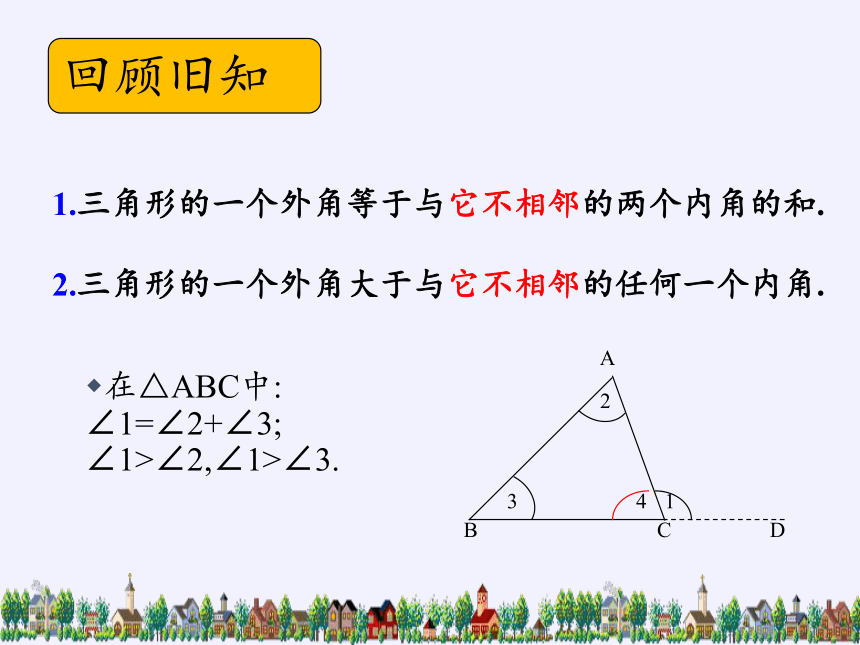
1.三角形的一个外角等于与它不相邻的两个内角的和.
2.三角形的一个外角大于与它不相邻的任何一个内角.
回顾旧知
A
B
C
D
1
2
3
4
在△ABC中:
∠1=∠2+∠3;
∠1>∠2,∠1>∠3.
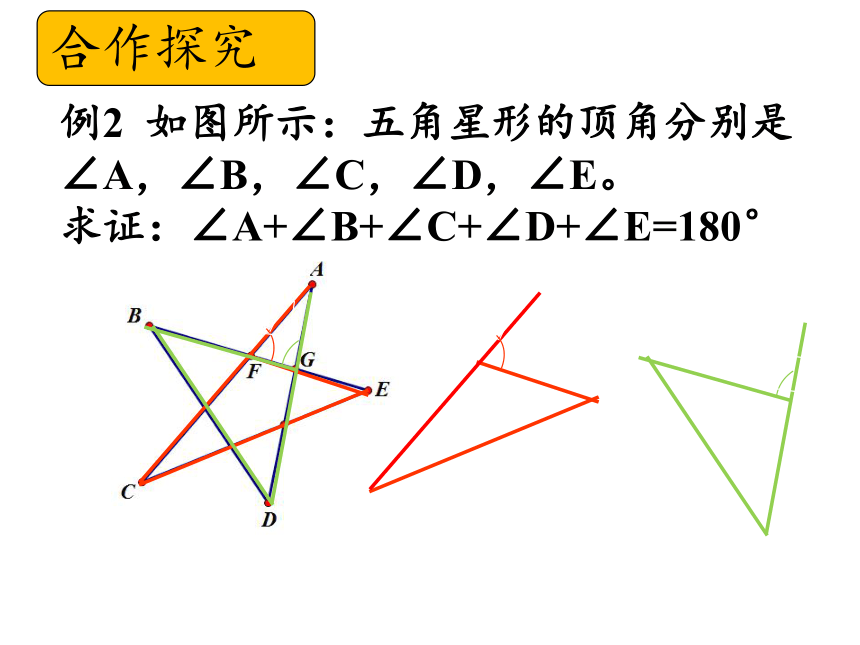
例2 如图所示:五角星形的顶角分别是
∠A,∠B,∠C,∠D,∠E。
求证:∠A+∠B+∠C+∠D+∠E=180°
合作探究
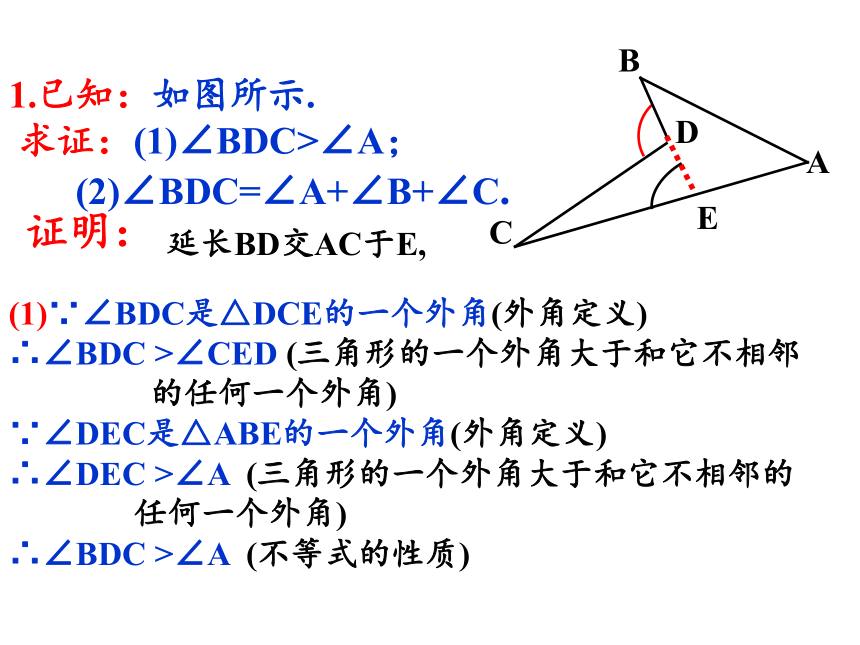
1.已知:如图所示.
求证:(1)∠BDC>∠A;
(2)∠BDC=∠A+∠B+∠C.
(1)∵∠BDC是△DCE的一个外角(外角定义)
∴∠BDC >∠CED (三角形的一个外角大于和它不相邻
的任何一个外角)
∵∠DEC是△ABE的一个外角(外角定义)
∴∠DEC >∠A (三角形的一个外角大于和它不相邻的
任何一个外角)
∴∠BDC >∠A (不等式的性质)
B
C
A
D
E
证明:
延长BD交AC于E,
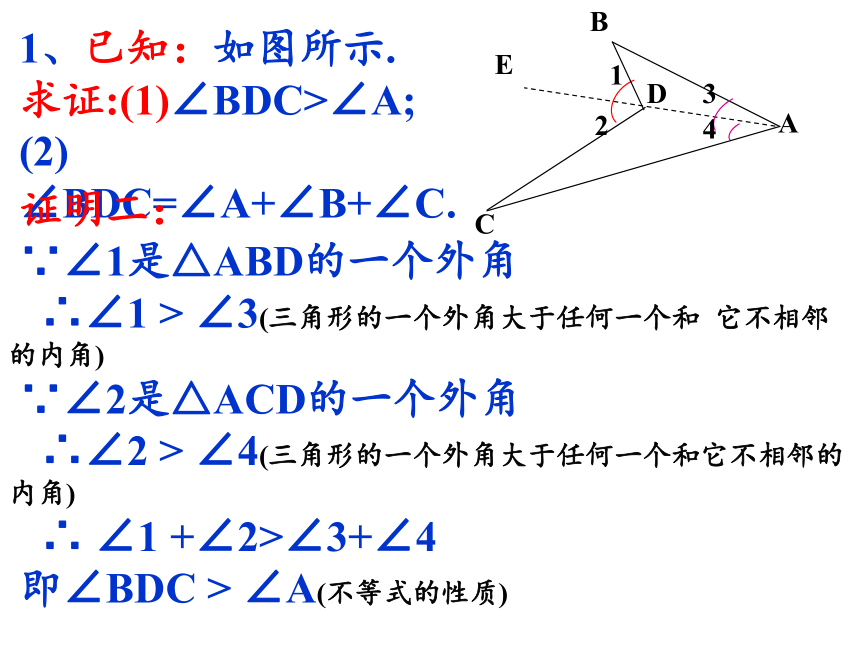
1、已知:如图所示.
求证:(1)∠BDC>∠A;
(2) ∠BDC=∠A+∠B+∠C.
证明二:
∵∠1是△ABD的一个外角
∴∠1 > ∠3(三角形的一个外角大于任何一个和 它不相邻的内角)
∵∠2是△ACD的一个外角
∴∠2 > ∠4(三角形的一个外角大于任何一个和它不相邻的内角)
∴ ∠1 +∠2>∠3+∠4
即∠BDC > ∠A(不等式的性质)
B
C
A
D
E
1
2
3
4
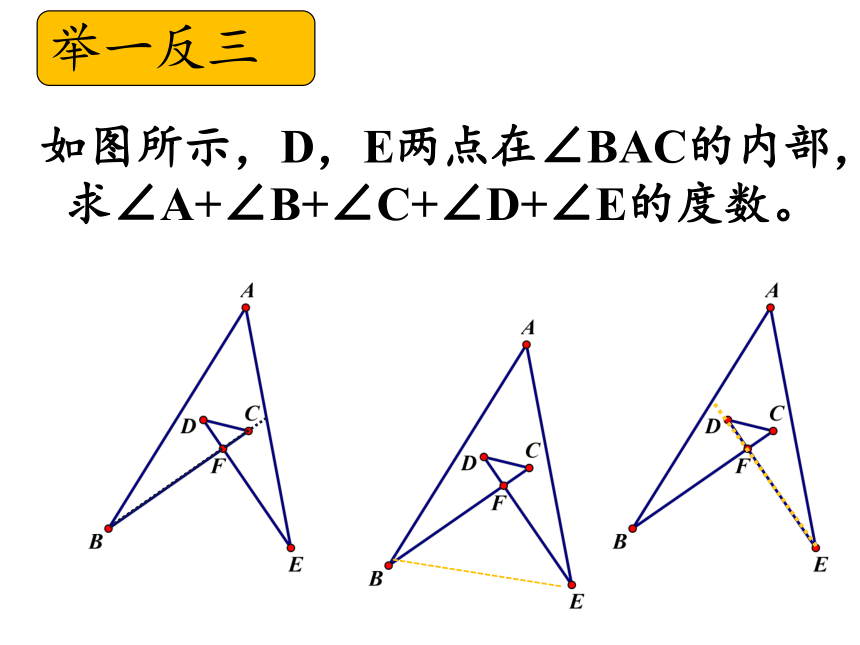
如图所示,D,E两点在∠BAC的内部,
求∠A+∠B+∠C+∠D+∠E的度数。
举一反三
拓展提升
1.如图,直线l1∥l2,直线l3与直线l1,l2分别交于C,D两点,有一点P在C,D之间运动(不与C,D两点重合),在它运动过程中,试分析∠1 、∠2 、∠3三者之间的关系?你能选用两种方法说明得到的关系吗?
如图,直线l1∥l2,直线l3与直线l1,l2分别交于C,D两点,有一点P在C,D之间运动(不与C,D两点重合),在它运动过程中,试分析∠1 、∠2 、∠3三者之间的关系?你能选用两种方法说明得到的关系吗?
2.如图,纸片△ABC中,∠C=45 ,∠B=115 ,将纸片的一角折叠,使A落在△ABC外,则∠1 ∠2等于
1
2
3.小明把一副含45 ,30 的直角三角板如图摆放,其中∠C=∠F=90 ,∠A=45 ,∠D=30 ,则∠α+∠β等于
必做题:P58随堂练习1、2 知识技能2
选做题:P59数学理解3
作业布置
我们的收获
谢 谢
三角形外角定理
1.能够灵活运用三角形内角和定理及两个推论解决问题。
2.经历从不同角度寻求分析问题和解决问题的过程,体验解决问题方法的多样性
3.养成独立思考、合作交流的学习习惯
学习目标
1.三角形的一个外角等于与它不相邻的两个内角的和.
2.三角形的一个外角大于与它不相邻的任何一个内角.
回顾旧知
A
B
C
D
1
2
3
4
在△ABC中:
∠1=∠2+∠3;
∠1>∠2,∠1>∠3.
例2 如图所示:五角星形的顶角分别是
∠A,∠B,∠C,∠D,∠E。
求证:∠A+∠B+∠C+∠D+∠E=180°
合作探究
1.已知:如图所示.
求证:(1)∠BDC>∠A;
(2)∠BDC=∠A+∠B+∠C.
(1)∵∠BDC是△DCE的一个外角(外角定义)
∴∠BDC >∠CED (三角形的一个外角大于和它不相邻
的任何一个外角)
∵∠DEC是△ABE的一个外角(外角定义)
∴∠DEC >∠A (三角形的一个外角大于和它不相邻的
任何一个外角)
∴∠BDC >∠A (不等式的性质)
B
C
A
D
E
证明:
延长BD交AC于E,
1、已知:如图所示.
求证:(1)∠BDC>∠A;
(2) ∠BDC=∠A+∠B+∠C.
证明二:
∵∠1是△ABD的一个外角
∴∠1 > ∠3(三角形的一个外角大于任何一个和 它不相邻的内角)
∵∠2是△ACD的一个外角
∴∠2 > ∠4(三角形的一个外角大于任何一个和它不相邻的内角)
∴ ∠1 +∠2>∠3+∠4
即∠BDC > ∠A(不等式的性质)
B
C
A
D
E
1
2
3
4
如图所示,D,E两点在∠BAC的内部,
求∠A+∠B+∠C+∠D+∠E的度数。
举一反三
拓展提升
1.如图,直线l1∥l2,直线l3与直线l1,l2分别交于C,D两点,有一点P在C,D之间运动(不与C,D两点重合),在它运动过程中,试分析∠1 、∠2 、∠3三者之间的关系?你能选用两种方法说明得到的关系吗?
如图,直线l1∥l2,直线l3与直线l1,l2分别交于C,D两点,有一点P在C,D之间运动(不与C,D两点重合),在它运动过程中,试分析∠1 、∠2 、∠3三者之间的关系?你能选用两种方法说明得到的关系吗?
2.如图,纸片△ABC中,∠C=45 ,∠B=115 ,将纸片的一角折叠,使A落在△ABC外,则∠1 ∠2等于
1
2
3.小明把一副含45 ,30 的直角三角板如图摆放,其中∠C=∠F=90 ,∠A=45 ,∠D=30 ,则∠α+∠β等于
必做题:P58随堂练习1、2 知识技能2
选做题:P59数学理解3
作业布置
我们的收获
谢 谢
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
