鲁教版(五四制)数学七年级下册 8.6 三角形内角和定理 课件(共22张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学七年级下册 8.6 三角形内角和定理 课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 969.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-18 12:59:27 | ||
图片预览





文档简介
(共22张PPT)
三角形内角和定理
我们知道三角形三个内角的和等于1800.
你还记得这个结论的探索过程吗
图1
图2
图3
A
B
C
C
B
A
A
B
B
C
C
A
B
我们知道三角形三个内角的和等于1800.
你还记得这个结论的探索过程吗
B
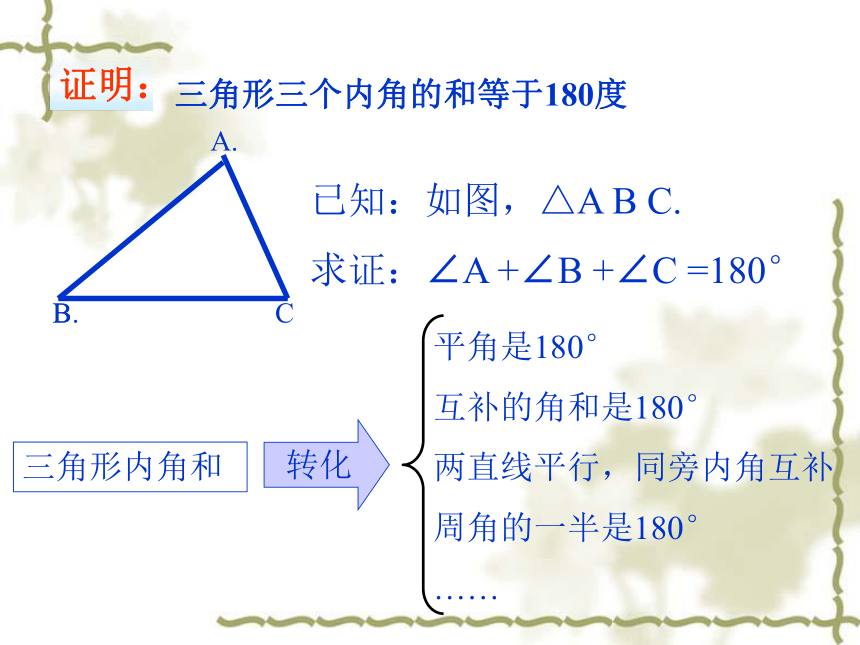
三角形三个内角的和等于180度
证明:
A.
B
C
B.
已知:如图,△A B C.
求证:∠A +∠B +∠C =180°
平角是180°
互补的角和是180°
两直线平行,同旁内角互补
周角的一半是180°
……
转化
三角形内角和
三角形三个内角的和等于180度
证明:
A.
B
C
B.
已知:如图,△A B C.
求证:∠A +∠B +∠C =180°
图3
A
B
C
B
图1
B
C
C
B
图2
B
C
A
B
A
A
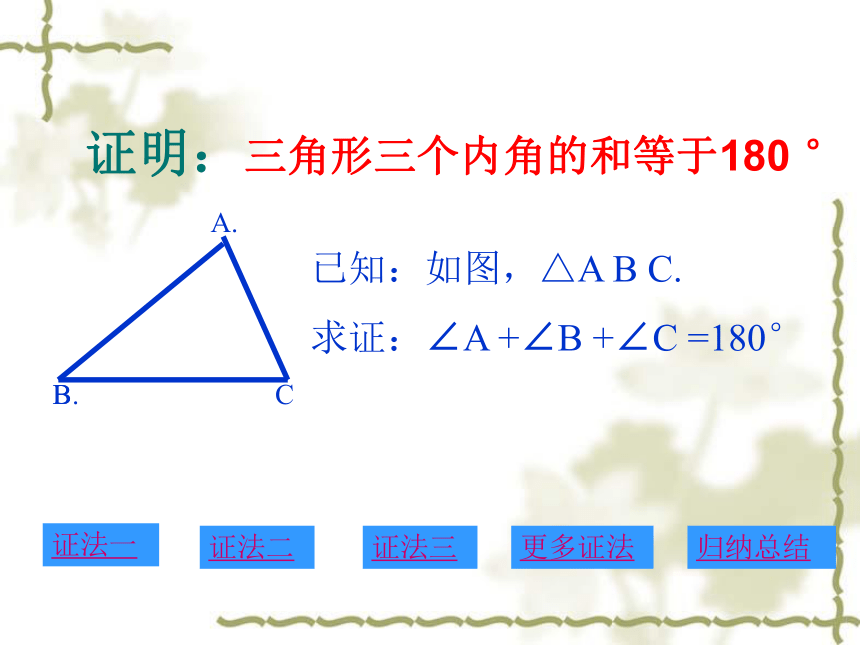
证明:三角形三个内角的和等于180 °
已知:如图,△A B C.
求证:∠A +∠B +∠C =180°
证法一
证法二
A.
B
C
B.
证法三
更多证法
归纳总结
F
2
1
E
C
B
A
三角形三个内角的和等于1800.
证明:过点A作EF∥BC,
∴∠B=∠2
∠C=∠1
又∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°
证法一
这里的EF称为辅助线,辅助线通常画成虚线.
2
1
E
D
C
B
A
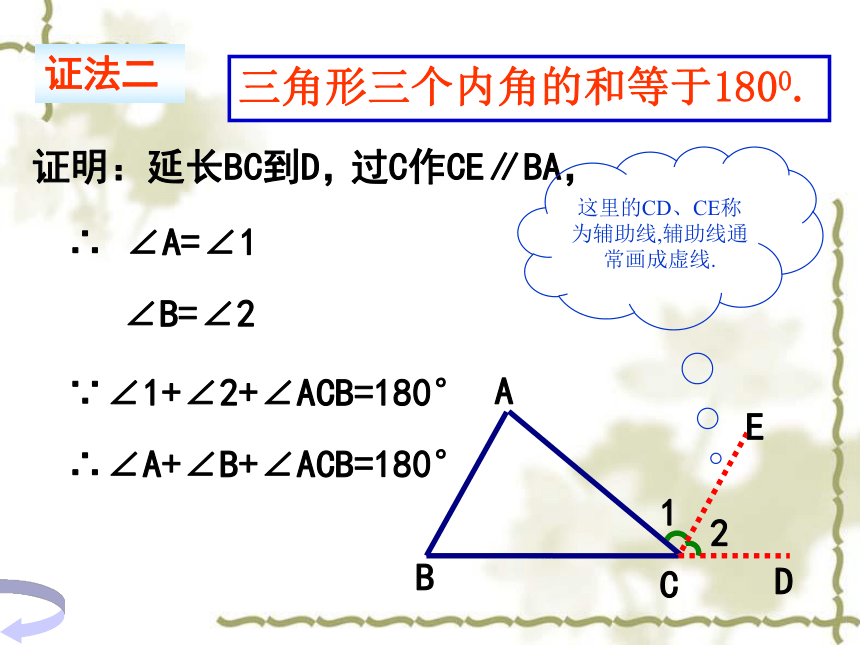
三角形三个内角的和等于1800.
证明:延长BC到D,
过C作CE∥BA,
∴ ∠A=∠1
∠B=∠2
∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
证法二
这里的CD、CE称为辅助线,辅助线通常画成虚线.
C
B
E
A
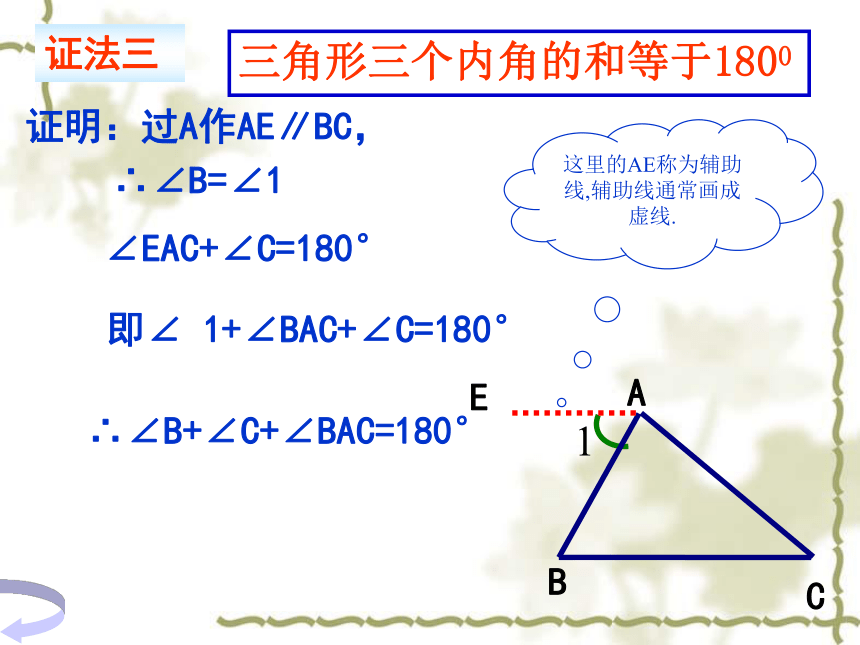
证明:过A作AE∥BC,
∴∠B=∠1
∠EAC+∠C=180°
即∠ 1+∠BAC+∠C=180°
∴∠B+∠C+∠BAC=180°
证法三
1
三角形三个内角的和等于1800
这里的AE称为辅助线,辅助线通常画成虚线.
E
A
B
C
D
F
图2
A
N
B
C
T
S
图3
P
Q
R
M
A
N
B
C
T
S
图4
P
Q
R
M
添加辅助线思路:1、构造平角
2、构造同旁内角
A
B
C
E
图1
F
D
总结归纳
三角形的三个内角的和是180°
A
B
C
几何语言:在△ABC中, ∠A +∠B +∠C=180°
定理:
学以致用
A
B
C
已知:在△ABC中, ∠B =60°,∠C=80°
求∠A 等于多少度?
解:在△ABC中,
∠A +∠B +∠C=180 °
又∵ ∠B =60 °
∠C =80°
∴∠A =40°
学以致用
A
B
C
D
如图,在△A B C中,已知∠B=40°,∠C=60°,AD平分
∠BAC,求∠ADB的度数。
1
2
定理: 直角三角形中,两锐角互余。
C
B
A
几何语言:△A B C 中∠C =90°,
∴∠A +∠B =90°
1、已知:如图,△A B C 中∠C =90°
求证: ∠A +∠B =90°
证明:在△ABC中,
∠A +∠B +∠C=180 °
又∵ ∠C =90°
∴∠A +∠B =90°
巩固提高
定理: 有两个角互余的三角形是直角三角形。
C
B
A
几何语言: ∵ ∠A +∠B =90°
∴∠C =90°
2、已知:如图,△A B C 中∠A +∠B =90°
求证: ∠C =90°
证明:在△ABC中,
∠A +∠B +∠C=180 °
又∵ ∠A +∠B =90°
∴∠C =90°
巩固提高
C
B
A
3、已知:如图,四边形A B C D是任意一个四边形
求证: ∠A +∠B +∠C+∠D =360°
D
方法一
方法二
巩固提高
定理: 四边形的内角和等于3600
C
B
A
几何语言:四边形A B C D中∠A +∠B +∠C+∠D =360°
巩固提升
3、已知:如图,四边形A B C D是任意一个四边形
求证: ∠A +∠B +∠C+∠D =360°
证明:连接AC
在△ABC中,∠1 +∠B +∠2=180°
在△ADC中,∠3 +∠D +∠4=180°
∴ ∠1+∠3+∠B+∠D+∠2+∠4=360°
即∠DAB +∠B +∠BCD+∠D =360°
D
4
3
2
1
返回
巩固提高
定理: 四边形的内角和等于3600
C
B
A
几何语言:四边形A B C D中∠A +∠B +∠C+∠D =360°
3、已知:如图,四边形A B C D是任意一个四边形
求证: ∠A +∠B +∠C+∠D =360°
证明:连接BD
在△ABD中,∠1 +∠A +∠2=180°
在△CBD中,∠3 +∠C +∠4=180°
∴ ∠1+∠3+∠A+∠C+∠2+∠4=360°
即∠A +∠ABC +∠C+∠CDA =360°
D
4
3
2
1
返回
巩固提高
注意:这里有一个基本图形“X形”,
它有一个数量关系: ∠A +∠B =∠C+∠D
巩固提升
4、如图:∠α= 。
320
440
α
480
C
B
A
D
O
巩固提高
A
O
D
C
B
说一说,这节课你有什么收获?还有哪些疑惑?
已知:如图,在△A B C中,DE//BC, ∠A=60°,∠C=70°,求证:∠ADE=50°
D
E
三角形内角和定理
我们知道三角形三个内角的和等于1800.
你还记得这个结论的探索过程吗
图1
图2
图3
A
B
C
C
B
A
A
B
B
C
C
A
B
我们知道三角形三个内角的和等于1800.
你还记得这个结论的探索过程吗
B
三角形三个内角的和等于180度
证明:
A.
B
C
B.
已知:如图,△A B C.
求证:∠A +∠B +∠C =180°
平角是180°
互补的角和是180°
两直线平行,同旁内角互补
周角的一半是180°
……
转化
三角形内角和
三角形三个内角的和等于180度
证明:
A.
B
C
B.
已知:如图,△A B C.
求证:∠A +∠B +∠C =180°
图3
A
B
C
B
图1
B
C
C
B
图2
B
C
A
B
A
A
证明:三角形三个内角的和等于180 °
已知:如图,△A B C.
求证:∠A +∠B +∠C =180°
证法一
证法二
A.
B
C
B.
证法三
更多证法
归纳总结
F
2
1
E
C
B
A
三角形三个内角的和等于1800.
证明:过点A作EF∥BC,
∴∠B=∠2
∠C=∠1
又∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°
证法一
这里的EF称为辅助线,辅助线通常画成虚线.
2
1
E
D
C
B
A
三角形三个内角的和等于1800.
证明:延长BC到D,
过C作CE∥BA,
∴ ∠A=∠1
∠B=∠2
∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
证法二
这里的CD、CE称为辅助线,辅助线通常画成虚线.
C
B
E
A
证明:过A作AE∥BC,
∴∠B=∠1
∠EAC+∠C=180°
即∠ 1+∠BAC+∠C=180°
∴∠B+∠C+∠BAC=180°
证法三
1
三角形三个内角的和等于1800
这里的AE称为辅助线,辅助线通常画成虚线.
E
A
B
C
D
F
图2
A
N
B
C
T
S
图3
P
Q
R
M
A
N
B
C
T
S
图4
P
Q
R
M
添加辅助线思路:1、构造平角
2、构造同旁内角
A
B
C
E
图1
F
D
总结归纳
三角形的三个内角的和是180°
A
B
C
几何语言:在△ABC中, ∠A +∠B +∠C=180°
定理:
学以致用
A
B
C
已知:在△ABC中, ∠B =60°,∠C=80°
求∠A 等于多少度?
解:在△ABC中,
∠A +∠B +∠C=180 °
又∵ ∠B =60 °
∠C =80°
∴∠A =40°
学以致用
A
B
C
D
如图,在△A B C中,已知∠B=40°,∠C=60°,AD平分
∠BAC,求∠ADB的度数。
1
2
定理: 直角三角形中,两锐角互余。
C
B
A
几何语言:△A B C 中∠C =90°,
∴∠A +∠B =90°
1、已知:如图,△A B C 中∠C =90°
求证: ∠A +∠B =90°
证明:在△ABC中,
∠A +∠B +∠C=180 °
又∵ ∠C =90°
∴∠A +∠B =90°
巩固提高
定理: 有两个角互余的三角形是直角三角形。
C
B
A
几何语言: ∵ ∠A +∠B =90°
∴∠C =90°
2、已知:如图,△A B C 中∠A +∠B =90°
求证: ∠C =90°
证明:在△ABC中,
∠A +∠B +∠C=180 °
又∵ ∠A +∠B =90°
∴∠C =90°
巩固提高
C
B
A
3、已知:如图,四边形A B C D是任意一个四边形
求证: ∠A +∠B +∠C+∠D =360°
D
方法一
方法二
巩固提高
定理: 四边形的内角和等于3600
C
B
A
几何语言:四边形A B C D中∠A +∠B +∠C+∠D =360°
巩固提升
3、已知:如图,四边形A B C D是任意一个四边形
求证: ∠A +∠B +∠C+∠D =360°
证明:连接AC
在△ABC中,∠1 +∠B +∠2=180°
在△ADC中,∠3 +∠D +∠4=180°
∴ ∠1+∠3+∠B+∠D+∠2+∠4=360°
即∠DAB +∠B +∠BCD+∠D =360°
D
4
3
2
1
返回
巩固提高
定理: 四边形的内角和等于3600
C
B
A
几何语言:四边形A B C D中∠A +∠B +∠C+∠D =360°
3、已知:如图,四边形A B C D是任意一个四边形
求证: ∠A +∠B +∠C+∠D =360°
证明:连接BD
在△ABD中,∠1 +∠A +∠2=180°
在△CBD中,∠3 +∠C +∠4=180°
∴ ∠1+∠3+∠A+∠C+∠2+∠4=360°
即∠A +∠ABC +∠C+∠CDA =360°
D
4
3
2
1
返回
巩固提高
注意:这里有一个基本图形“X形”,
它有一个数量关系: ∠A +∠B =∠C+∠D
巩固提升
4、如图:∠α= 。
320
440
α
480
C
B
A
D
O
巩固提高
A
O
D
C
B
说一说,这节课你有什么收获?还有哪些疑惑?
已知:如图,在△A B C中,DE//BC, ∠A=60°,∠C=70°,求证:∠ADE=50°
D
E
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
