2021-2022学年青岛版数学八年级下册6.4三角形的中位线定理课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年青岛版数学八年级下册6.4三角形的中位线定理课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-18 20:09:01 | ||
图片预览


文档简介
(共21张PPT)
6.4 三角形的中位线定理
学习目标
1. 理解三角形的中位线概念
2. 探索并掌握三角形的中位线定理
3. 会利用三角形的中位线定理进行计算和证明
温故知新
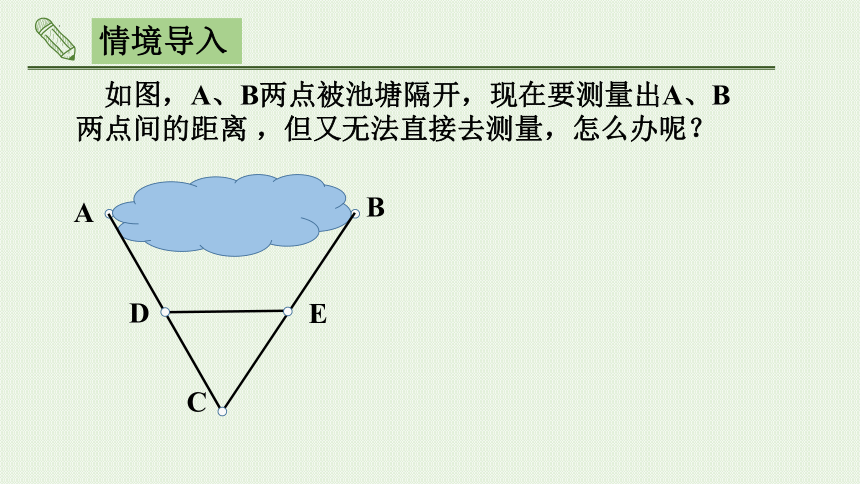
情境导入
如图,A、B两点被池塘隔开,现在要测量出A、B两点间的距离 ,但又无法直接去测量,怎么办呢?
A
B
C
D
E
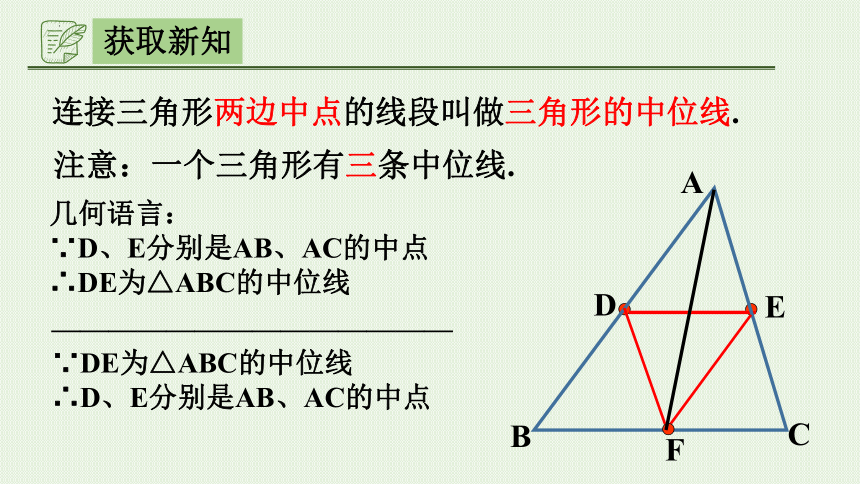
获取新知
D
E
A
B
C
连接三角形两边中点的线段叫做三角形的中位线.
F
注意:一个三角形有三条中位线.
几何语言:
∵D、E分别是AB、AC的中点
∴DE为△ABC的中位线
——————————————
∵DE为△ABC的中位线
∴D、E分别是AB、AC的中点
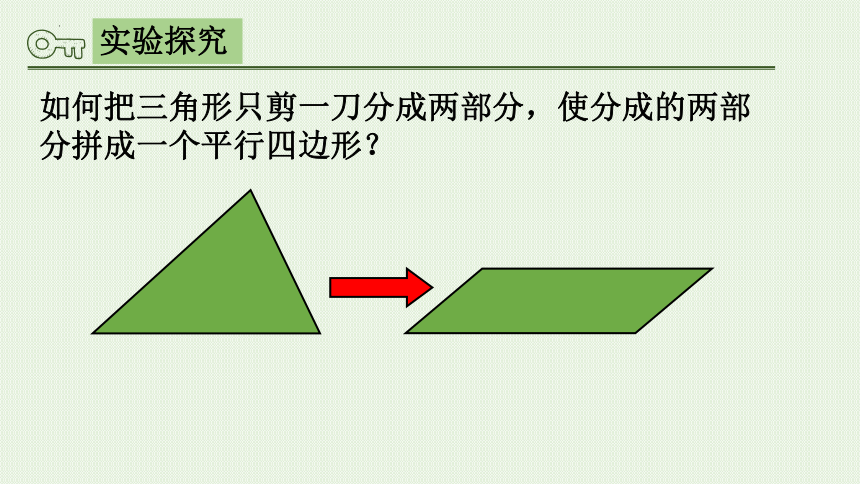
实验探究
如何把三角形只剪一刀分成两部分,使分成的两部分拼成一个平行四边形?
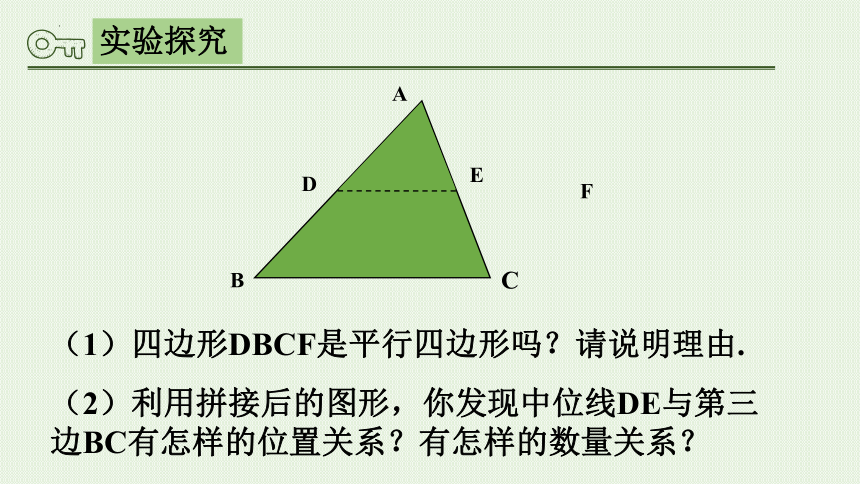
实验探究
B
F
D
A
C
E
(1)四边形DBCF是平行四边形吗?请说明理由.
(2)利用拼接后的图形,你发现中位线DE与第三边BC有怎样的位置关系?有怎样的数量关系?
实验探究
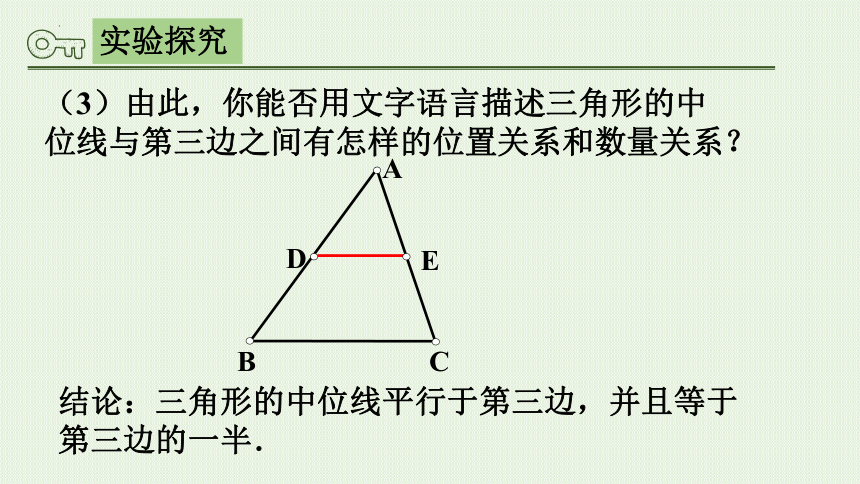
(3)由此,你能否用文字语言描述三角形的中位线与第三边之间有怎样的位置关系和数量关系?
C
A
B
D
E
结论:三角形的中位线平行于第三边,并且等于第三边的一半.
获取新知
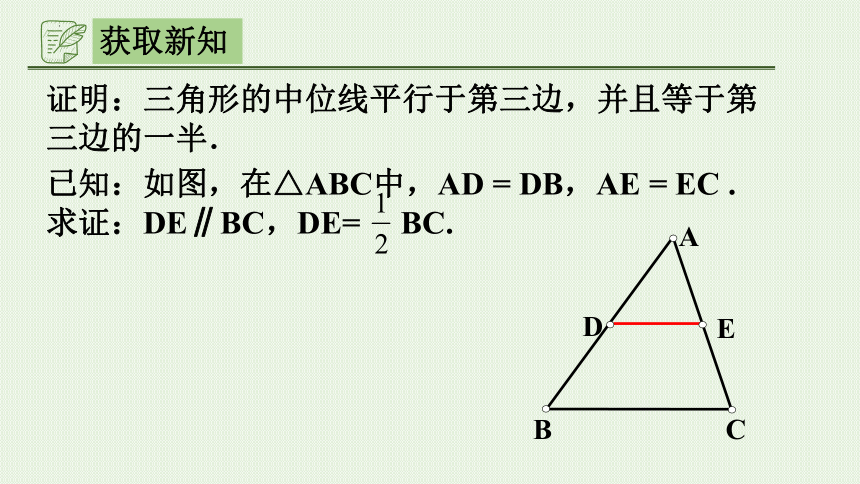
证明:三角形的中位线平行于第三边,并且等于第三边的一半.
C
A
B
D
E
已知:如图,在△ABC中,AD = DB,AE = EC . 求证:DE∥BC,DE= BC.
获取新知
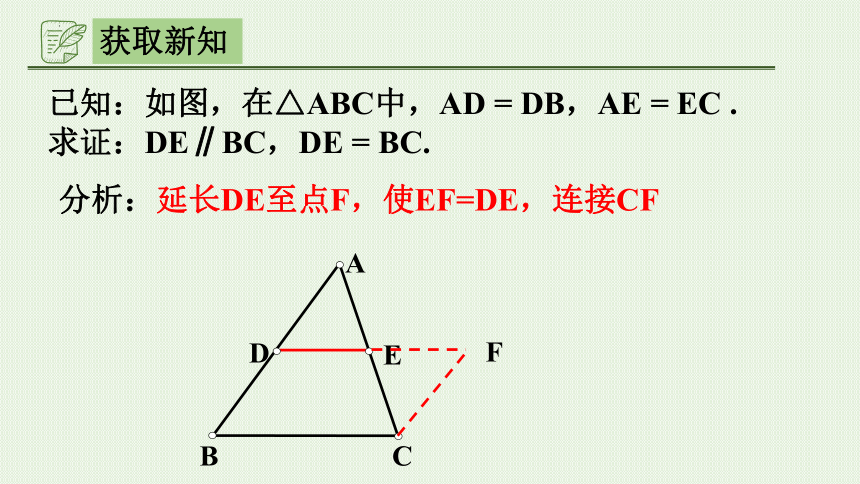
已知:如图,在△ABC中,AD = DB,AE = EC . 求证:DE∥BC,DE = BC.
C
A
B
D
E
F
分析:延长DE至点F,使EF=DE,连接CF
获取新知
已知:如图,在△ABC中,AD = DB,AE = EC . 求证:DE∥BC,DE = BC.
C
A
B
D
E
F
分析:过点C作AB的平行线,交DE的延长线于点F
获取新知
三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
D
A
B
C
E
用途: 证明平行问题
证明一条线段是另一条线段的两倍或一半
几何语言:
∵DE是△ABC的中位线
∴ DE∥BC,DE= BC.
跟踪练习
1.在△ABC中,D、E、F分别是AB、BC、AC的中点
①若∠ADF=65°,则∠B=_____度;
②若BC=8cm,则DF=______cm;
③若AC=6cm,BC=8cm,AB=4cm,则△DEF的周长= ______cm ;
A
C
B
F
D
E
跟踪练习
2.已知:△ABC中,D是BC上一点,DC=AC,CF⊥AD,垂足是F,E是AB的中点.若EF=5cm,则BD=_____cm.
跟踪练习
A
B
C
D
E
常用辅助线:已知两边中点,补全第三边
目的:构造三角形,利用中位线定理来解决
典型例题
例1. 如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点. 求证:四边形EFGH是平行四边形.
A
B
C
D
E
F
G
H
证明:
变式练习
已知:在△ABC中,AD是中线,EF是中位线,求证:AD、EF互相平分.
常用的辅助线:中点连中点,构造中位线,发挥中位线定理的作用
课堂小结
一定义
一定理
一思想
一方法
通过本节课学习,有哪些收获?
当堂检测
2.如图,D、E、F分别是△ABC各边的中点,若△DEF 的周长为12cm,则△ABC 的周长为_____;若△ABC的面积等于16cm2,则△DEF的面积为_____.
A
B
C
D
E
F
1.顺次连结等腰梯形各边中点所得的四边形是_________.
当堂检测
3.如图,点D、E、F分别是△ABC各边的中点,BH⊥AC,垂足为H,DE=6cm.则FH的长为.
C
A
B
D
E
F
H
谢谢
请输入您的标题
备用页
6.4 三角形的中位线定理
学习目标
1. 理解三角形的中位线概念
2. 探索并掌握三角形的中位线定理
3. 会利用三角形的中位线定理进行计算和证明
温故知新
情境导入
如图,A、B两点被池塘隔开,现在要测量出A、B两点间的距离 ,但又无法直接去测量,怎么办呢?
A
B
C
D
E
获取新知
D
E
A
B
C
连接三角形两边中点的线段叫做三角形的中位线.
F
注意:一个三角形有三条中位线.
几何语言:
∵D、E分别是AB、AC的中点
∴DE为△ABC的中位线
——————————————
∵DE为△ABC的中位线
∴D、E分别是AB、AC的中点
实验探究
如何把三角形只剪一刀分成两部分,使分成的两部分拼成一个平行四边形?
实验探究
B
F
D
A
C
E
(1)四边形DBCF是平行四边形吗?请说明理由.
(2)利用拼接后的图形,你发现中位线DE与第三边BC有怎样的位置关系?有怎样的数量关系?
实验探究
(3)由此,你能否用文字语言描述三角形的中位线与第三边之间有怎样的位置关系和数量关系?
C
A
B
D
E
结论:三角形的中位线平行于第三边,并且等于第三边的一半.
获取新知
证明:三角形的中位线平行于第三边,并且等于第三边的一半.
C
A
B
D
E
已知:如图,在△ABC中,AD = DB,AE = EC . 求证:DE∥BC,DE= BC.
获取新知
已知:如图,在△ABC中,AD = DB,AE = EC . 求证:DE∥BC,DE = BC.
C
A
B
D
E
F
分析:延长DE至点F,使EF=DE,连接CF
获取新知
已知:如图,在△ABC中,AD = DB,AE = EC . 求证:DE∥BC,DE = BC.
C
A
B
D
E
F
分析:过点C作AB的平行线,交DE的延长线于点F
获取新知
三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
D
A
B
C
E
用途: 证明平行问题
证明一条线段是另一条线段的两倍或一半
几何语言:
∵DE是△ABC的中位线
∴ DE∥BC,DE= BC.
跟踪练习
1.在△ABC中,D、E、F分别是AB、BC、AC的中点
①若∠ADF=65°,则∠B=_____度;
②若BC=8cm,则DF=______cm;
③若AC=6cm,BC=8cm,AB=4cm,则△DEF的周长= ______cm ;
A
C
B
F
D
E
跟踪练习
2.已知:△ABC中,D是BC上一点,DC=AC,CF⊥AD,垂足是F,E是AB的中点.若EF=5cm,则BD=_____cm.
跟踪练习
A
B
C
D
E
常用辅助线:已知两边中点,补全第三边
目的:构造三角形,利用中位线定理来解决
典型例题
例1. 如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点. 求证:四边形EFGH是平行四边形.
A
B
C
D
E
F
G
H
证明:
变式练习
已知:在△ABC中,AD是中线,EF是中位线,求证:AD、EF互相平分.
常用的辅助线:中点连中点,构造中位线,发挥中位线定理的作用
课堂小结
一定义
一定理
一思想
一方法
通过本节课学习,有哪些收获?
当堂检测
2.如图,D、E、F分别是△ABC各边的中点,若△DEF 的周长为12cm,则△ABC 的周长为_____;若△ABC的面积等于16cm2,则△DEF的面积为_____.
A
B
C
D
E
F
1.顺次连结等腰梯形各边中点所得的四边形是_________.
当堂检测
3.如图,点D、E、F分别是△ABC各边的中点,BH⊥AC,垂足为H,DE=6cm.则FH的长为.
C
A
B
D
E
F
H
谢谢
请输入您的标题
备用页
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
