2022-2023学年人教版八年级数学上册12.2三角形全等判定基础测试卷 (Word版含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册12.2三角形全等判定基础测试卷 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 564.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-19 06:22:56 | ||
图片预览


文档简介
12.2三角形全等判定基础测试卷
一、单选题
1.下列关于全等三角形的说法不正确的是
A.全等三角形的大小相等 B.两个等边三角形一定是全等三角形
C.全等三角形的形状相同 D.全等三角形的对应边相等
2.作平分线的作图过程如下:
作法:(1)在和上分别截取、,使.
(2)分别以,为圆心,大于的长为半径作弧,两弧交于点.
(3)作射线,则就是的平分线.
用下面的三角形全等的判定解释作图原理,最为恰当的是( )
A. B. C. D.
3.如图,在梯形中,,,,那么下列结论不正确的是( )
A. B.
C. D.
4.如图,AD是的角平分线,,垂足为F,,和的面积分别为60和35,则的面积为
A.25 B. C. D.
5.如图所示,是的边上的中线,cm,cm,则边的长度可能是( )
A.3cm B.5cm C.14cm D.13cm
6.如图,在中,,D是上一点,于点E,,连接,若,则等于( )
A. B. C. D.
7.如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,则∠BFD的度数是( )
A.60° B.90° C.45° D.120°
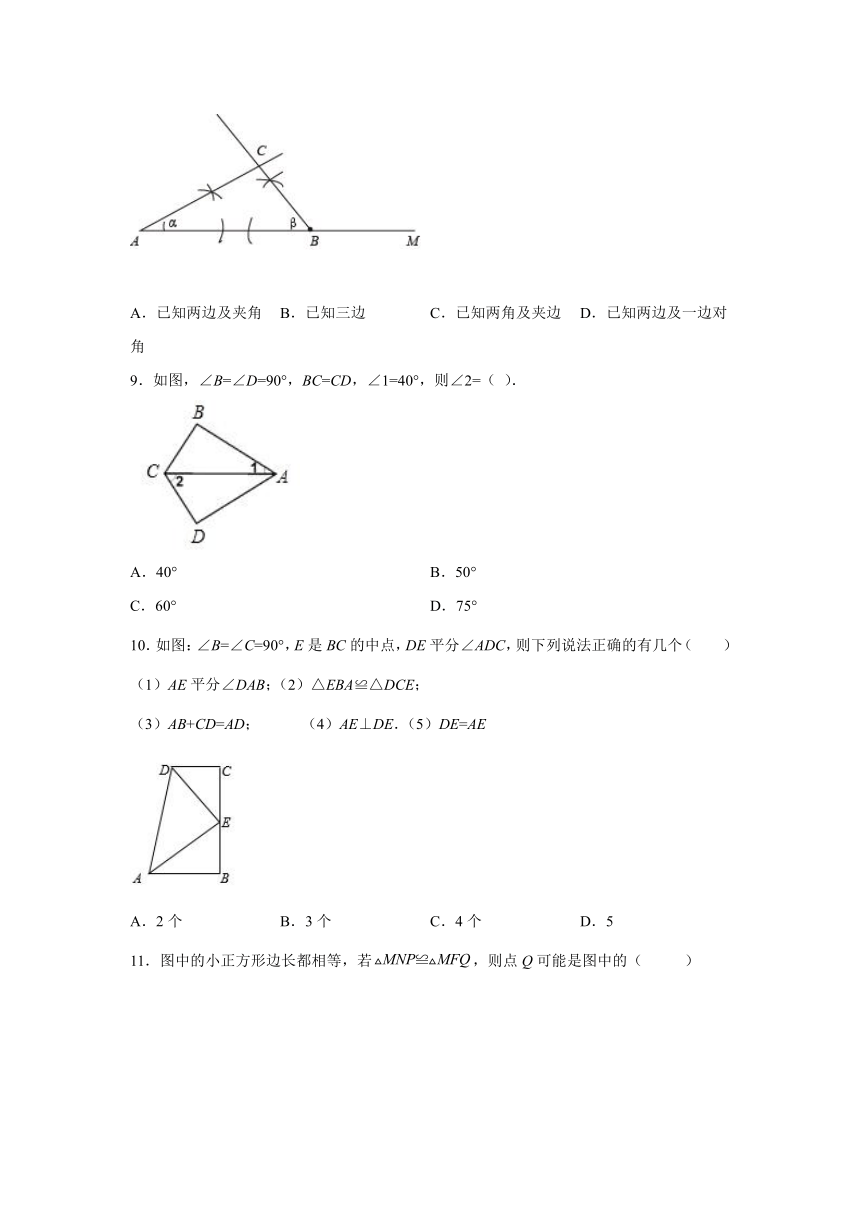
8.如图是作的作图痕迹,则此作图的已知条件是( )
A.已知两边及夹角 B.已知三边 C.已知两角及夹边 D.已知两边及一边对角
9.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=( ).
A.40° B.50°
C.60° D.75°
10.如图:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,则下列说法正确的有几个( )
(1)AE平分∠DAB;(2)△EBA≌△DCE;
(3)AB+CD=AD; (4)AE⊥DE.(5)DE=AE
A.2个 B.3个 C.4个 D.5
11.图中的小正方形边长都相等,若,则点Q可能是图中的( )
A.点D B.点C C.点B D.点A
12.如图,锐角△ABC的两条高BD、CE相交于点O,且CE=BD,若∠CBD=20°,则∠A的度数为( )
A.20° B.40° C.60° D.70°
二、填空题
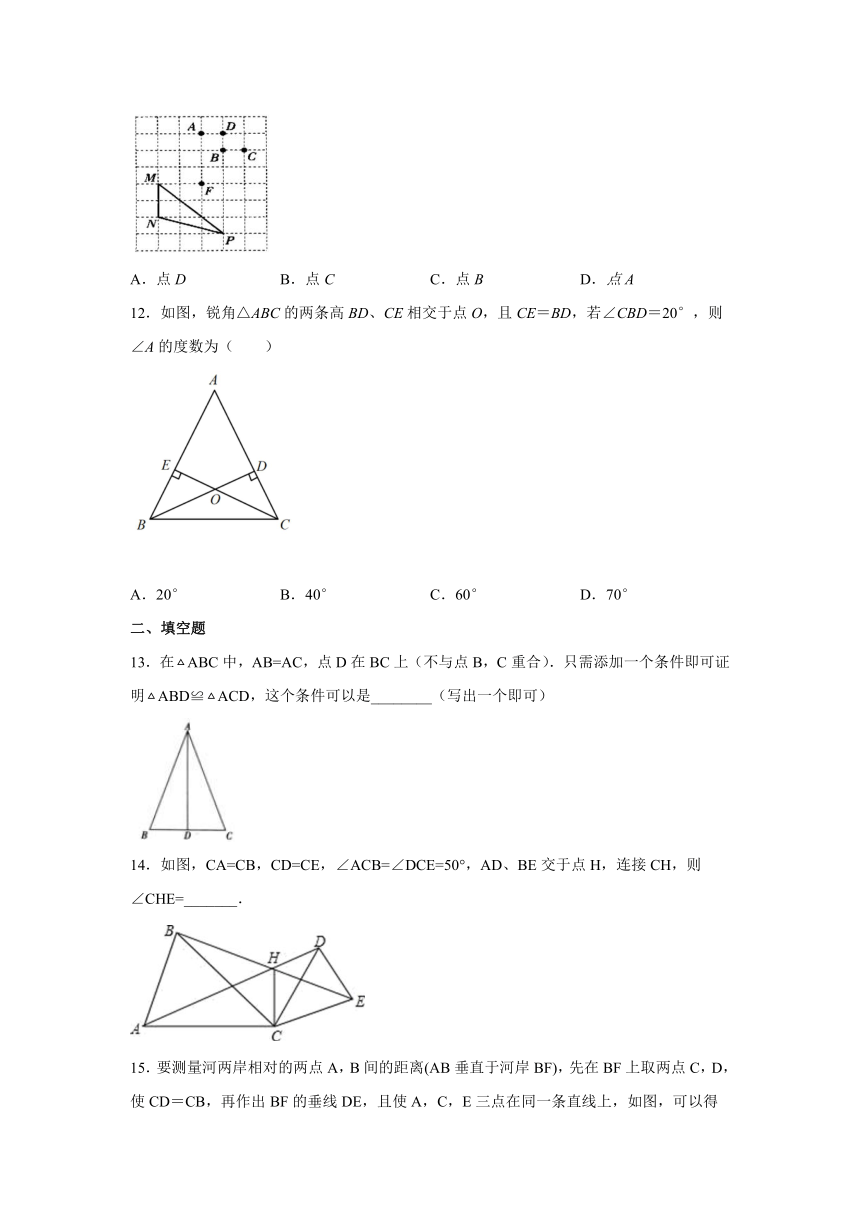
13.在ABC中,AB=AC,点D在BC上(不与点B,C重合).只需添加一个条件即可证明ABD≌ACD,这个条件可以是________(写出一个即可)
14.如图,CA=CB,CD=CE,∠ACB=∠DCE=50°,AD、BE交于点H,连接CH,则∠CHE=_______.
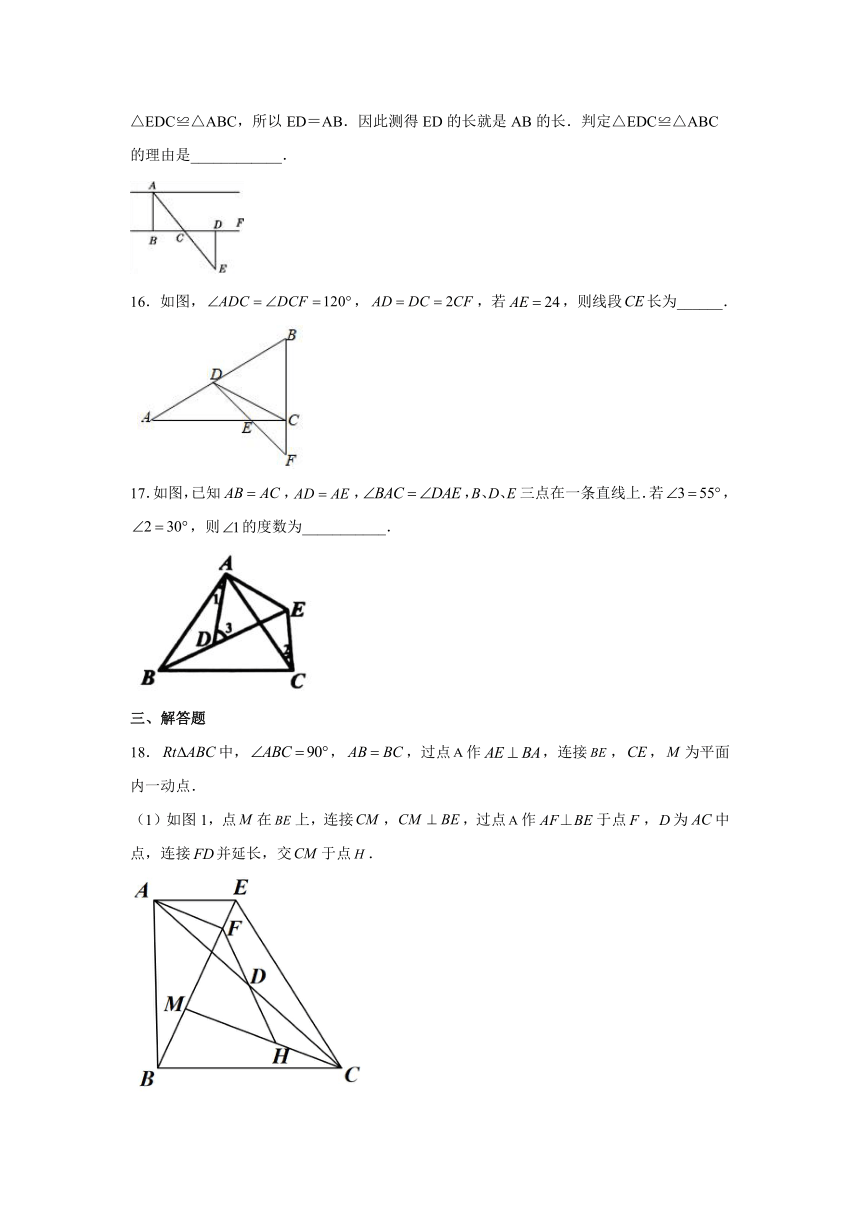
15.要测量河两岸相对的两点A,B间的距离(AB垂直于河岸BF),先在BF上取两点C,D,使CD=CB,再作出BF的垂线DE,且使A,C,E三点在同一条直线上,如图,可以得△EDC≌△ABC,所以ED=AB.因此测得ED的长就是AB的长.判定△EDC≌△ABC的理由是____________.
16.如图,,,若,则线段长为______.
17.如图,已知,,,B、D、E三点在一条直线上.若,,则的度数为___________.
三、解答题
18.中,,,过点作,连接,,为平面内一动点.
(1)如图1,点在上,连接,,过点作于点,为中点,连接并延长,交于点.
①若,,则 ;
②求证:.
(2)如图2,连接,,过点作于点,且满足,连接,,过点作于点,若,,,请求出线段的取值范围.
19.在中,,,为直线上一点,连接,过点作交于点,交于点,在直线上截取,连接.
(1)当点,都在线段上时,如图①,求证:;
(2)当点在线段的延长线上,点在线段的延长线上时,如图②;当点在线段的延长线上,点在线段的延长线上时,如图③,直接写出线段,,之间的数量关系,不需要证明.
20.已知:如图,点A、B、C、D在一条直线上,.
(1)求证:;
(2)若,求的度数.
21.如图,小明和小华两家位于A,B两处,隔河相望.要测得两家之间的距离,小明设计如下方案:从点B出发沿河岸画一条射线BF,在BF上截取,过点D作,取点E使E,C,A在同一条直线上,则DE的长就是A,B之间的距离,说明他设计的道理.
参考答案
1--10BAADB CBCBB 11--12AB
13.∠BAD=∠CAD(或BD=CD)
14.65°
15.ASA
16.8
17.25°
18.解:(1)①∵,,,
∴,
②∵,,
∴∠AFB=∠BMC=∠FMC =90°,
∴∠ABF+∠BAF=90°,
∵,
∴∠ABF+∠CBM=90°,
∴∠BAF=∠CBM,
∵,
∴△ABF≌△BCM,
∴BF=MC,AF=BM,
∵∠AFB=∠FMC =90°,
∴AF//CM,
∴∠FAC=∠HCD,
∵为中点,
∴AD=CD,
∵∠FDA=∠HDC,
∴△AFD≌△CHD,
∴AF=CH,
∴BM=CH,
∵BF=CM
∴BF-BM=CM-CH
∴.
(2)连接CM,
∵,,
∴∠ABC=∠=90°,
∴∠BA=∠CBM,
∵,,
∴△ ≌△CBM,
∴,
∵,,
∴∠ABC+∠BAE=180°,
∴AE//BC,
∴,
∵,,
∴,
∴EC=9
在△ECM中,,
则9-3≤CM≤9+3,
∴6≤CM≤12,
∴6≤≤12,
19.(1)证明:如图,过点作交的延长线于点.
0
∴.
∵,
∴,.
∵,
∴.
∴.
在和中,
∴.
∴,.
∵,,
∴.
∴.
∴.
∵,,
∴.
在和中,
∴.
∴.
∵,
∴.
(2)图②:.
证明:过点作交于点.
∴.
∵,
∴,.
∵,
∴.
∴.
在和中,
∴.
∴,.
∵,,
∴.
∴,
∵
∴.
∴.
∵,,
∴.
在和中,
∴.
∴.
∵,
∴.
图③:.
证明:如图,过点作交的延长线于点.
∴.
∵,
∴,.
∵,
∴.
∴.
在和中,
∴.
∴,.
∵,,
∴.
∴.
∴.
∵,,
∴.
在和中,
∴.
∴.
∵,
∴.
20.证明:(1)∵EA∥FB,
∴∠A=∠FBD,
∵AB=CD,
∴AB+BC=CD+BC,
即AC=BD,
在△EAC与△FBD中,
∴△EAC≌△FBD(SAS)
(2)∵△EAC≌△FBD,
∴∠ECA=∠D=80°,
∵∠A=40°,
∴∠E=180°-40°-80°=60°,
答:∠E的度数为60°.
21.解:,
,
在和中,
,
,
,
即的长就是、两点之间的距离.
一、单选题
1.下列关于全等三角形的说法不正确的是
A.全等三角形的大小相等 B.两个等边三角形一定是全等三角形
C.全等三角形的形状相同 D.全等三角形的对应边相等
2.作平分线的作图过程如下:
作法:(1)在和上分别截取、,使.
(2)分别以,为圆心,大于的长为半径作弧,两弧交于点.
(3)作射线,则就是的平分线.
用下面的三角形全等的判定解释作图原理,最为恰当的是( )
A. B. C. D.
3.如图,在梯形中,,,,那么下列结论不正确的是( )
A. B.
C. D.
4.如图,AD是的角平分线,,垂足为F,,和的面积分别为60和35,则的面积为
A.25 B. C. D.
5.如图所示,是的边上的中线,cm,cm,则边的长度可能是( )
A.3cm B.5cm C.14cm D.13cm
6.如图,在中,,D是上一点,于点E,,连接,若,则等于( )
A. B. C. D.
7.如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,则∠BFD的度数是( )
A.60° B.90° C.45° D.120°
8.如图是作的作图痕迹,则此作图的已知条件是( )
A.已知两边及夹角 B.已知三边 C.已知两角及夹边 D.已知两边及一边对角
9.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=( ).
A.40° B.50°
C.60° D.75°
10.如图:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,则下列说法正确的有几个( )
(1)AE平分∠DAB;(2)△EBA≌△DCE;
(3)AB+CD=AD; (4)AE⊥DE.(5)DE=AE
A.2个 B.3个 C.4个 D.5
11.图中的小正方形边长都相等,若,则点Q可能是图中的( )
A.点D B.点C C.点B D.点A
12.如图,锐角△ABC的两条高BD、CE相交于点O,且CE=BD,若∠CBD=20°,则∠A的度数为( )
A.20° B.40° C.60° D.70°
二、填空题
13.在ABC中,AB=AC,点D在BC上(不与点B,C重合).只需添加一个条件即可证明ABD≌ACD,这个条件可以是________(写出一个即可)
14.如图,CA=CB,CD=CE,∠ACB=∠DCE=50°,AD、BE交于点H,连接CH,则∠CHE=_______.
15.要测量河两岸相对的两点A,B间的距离(AB垂直于河岸BF),先在BF上取两点C,D,使CD=CB,再作出BF的垂线DE,且使A,C,E三点在同一条直线上,如图,可以得△EDC≌△ABC,所以ED=AB.因此测得ED的长就是AB的长.判定△EDC≌△ABC的理由是____________.
16.如图,,,若,则线段长为______.
17.如图,已知,,,B、D、E三点在一条直线上.若,,则的度数为___________.
三、解答题
18.中,,,过点作,连接,,为平面内一动点.
(1)如图1,点在上,连接,,过点作于点,为中点,连接并延长,交于点.
①若,,则 ;
②求证:.
(2)如图2,连接,,过点作于点,且满足,连接,,过点作于点,若,,,请求出线段的取值范围.
19.在中,,,为直线上一点,连接,过点作交于点,交于点,在直线上截取,连接.
(1)当点,都在线段上时,如图①,求证:;
(2)当点在线段的延长线上,点在线段的延长线上时,如图②;当点在线段的延长线上,点在线段的延长线上时,如图③,直接写出线段,,之间的数量关系,不需要证明.
20.已知:如图,点A、B、C、D在一条直线上,.
(1)求证:;
(2)若,求的度数.
21.如图,小明和小华两家位于A,B两处,隔河相望.要测得两家之间的距离,小明设计如下方案:从点B出发沿河岸画一条射线BF,在BF上截取,过点D作,取点E使E,C,A在同一条直线上,则DE的长就是A,B之间的距离,说明他设计的道理.
参考答案
1--10BAADB CBCBB 11--12AB
13.∠BAD=∠CAD(或BD=CD)
14.65°
15.ASA
16.8
17.25°
18.解:(1)①∵,,,
∴,
②∵,,
∴∠AFB=∠BMC=∠FMC =90°,
∴∠ABF+∠BAF=90°,
∵,
∴∠ABF+∠CBM=90°,
∴∠BAF=∠CBM,
∵,
∴△ABF≌△BCM,
∴BF=MC,AF=BM,
∵∠AFB=∠FMC =90°,
∴AF//CM,
∴∠FAC=∠HCD,
∵为中点,
∴AD=CD,
∵∠FDA=∠HDC,
∴△AFD≌△CHD,
∴AF=CH,
∴BM=CH,
∵BF=CM
∴BF-BM=CM-CH
∴.
(2)连接CM,
∵,,
∴∠ABC=∠=90°,
∴∠BA=∠CBM,
∵,,
∴△ ≌△CBM,
∴,
∵,,
∴∠ABC+∠BAE=180°,
∴AE//BC,
∴,
∵,,
∴,
∴EC=9
在△ECM中,,
则9-3≤CM≤9+3,
∴6≤CM≤12,
∴6≤≤12,
19.(1)证明:如图,过点作交的延长线于点.
0
∴.
∵,
∴,.
∵,
∴.
∴.
在和中,
∴.
∴,.
∵,,
∴.
∴.
∴.
∵,,
∴.
在和中,
∴.
∴.
∵,
∴.
(2)图②:.
证明:过点作交于点.
∴.
∵,
∴,.
∵,
∴.
∴.
在和中,
∴.
∴,.
∵,,
∴.
∴,
∵
∴.
∴.
∵,,
∴.
在和中,
∴.
∴.
∵,
∴.
图③:.
证明:如图,过点作交的延长线于点.
∴.
∵,
∴,.
∵,
∴.
∴.
在和中,
∴.
∴,.
∵,,
∴.
∴.
∴.
∵,,
∴.
在和中,
∴.
∴.
∵,
∴.
20.证明:(1)∵EA∥FB,
∴∠A=∠FBD,
∵AB=CD,
∴AB+BC=CD+BC,
即AC=BD,
在△EAC与△FBD中,
∴△EAC≌△FBD(SAS)
(2)∵△EAC≌△FBD,
∴∠ECA=∠D=80°,
∵∠A=40°,
∴∠E=180°-40°-80°=60°,
答:∠E的度数为60°.
21.解:,
,
在和中,
,
,
,
即的长就是、两点之间的距离.
