2022-2023学年北师大版九年级数学上册1.3 正方形的性质 课件(共16张PPT)
文档属性
| 名称 | 2022-2023学年北师大版九年级数学上册1.3 正方形的性质 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 300.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-18 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
第一章 特殊平行四边形
1.3.1 正方形的性质
北师大版九年级上册数学
新课导入
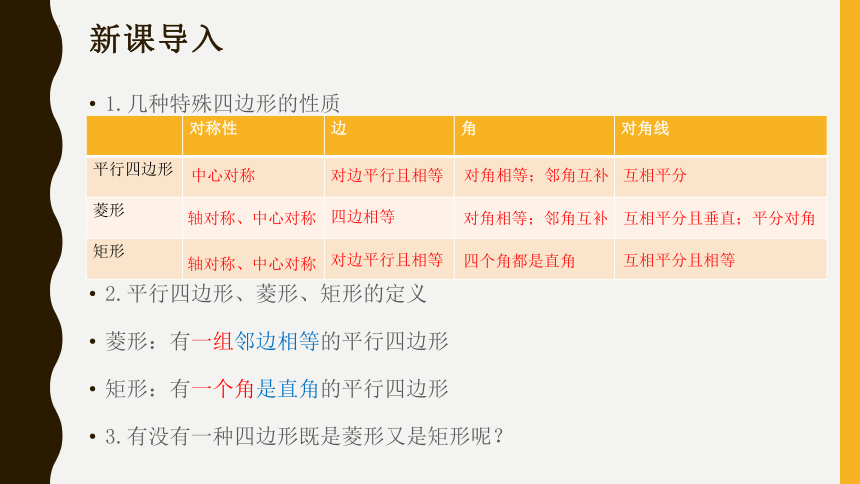
1.几种特殊四边形的性质
2.平行四边形、菱形、矩形的定义
菱形:有一组邻边相等的平行四边形
矩形:有一个角是直角的平行四边形
3.有没有一种四边形既是菱形又是矩形呢?
对称性 边 角 对角线
平行四边形
菱形
矩形
中心对称
轴对称、中心对称
轴对称、中心对称
对边平行且相等
四边相等
对边平行且相等
对角相等;邻角互补
对角相等;邻角互补
四个角都是直角
互相平分
互相平分且垂直;平分对角
互相平分且相等
学习目标
1.在对平行四边形、矩形、菱形的认识基础上探索正方形的性质,并能运用正方形的性质进行证明与计算.
2.进一步了解平行四边形、矩形、菱形及正方形之间的相互关系.
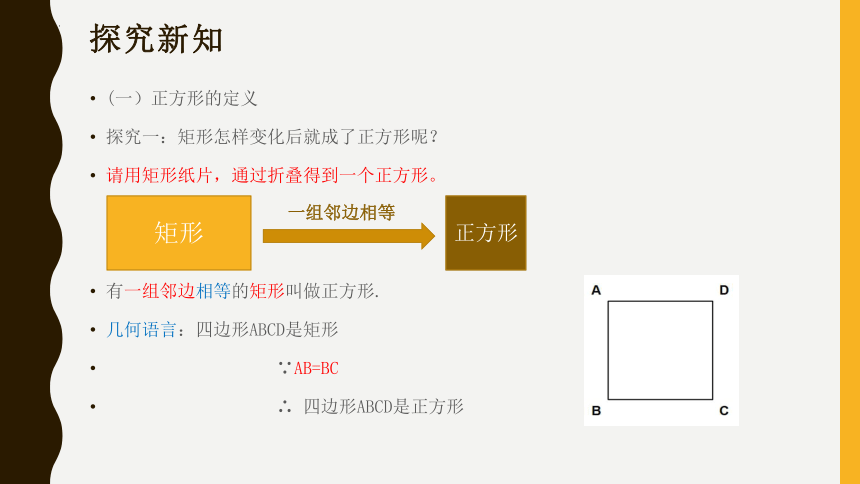
(一)正方形的定义
探究一:矩形怎样变化后就成了正方形呢?
请用矩形纸片,通过折叠得到一个正方形。
有一组邻边相等的矩形叫做正方形.
几何语言:四边形ABCD是矩形
∵AB=BC
∴ 四边形ABCD是正方形
探究新知
矩形
正方形
一组邻边相等
探究二:菱形怎样变化后就成了正方形呢?
有一个角是直角的菱形叫做正方形.
几何语言:四边形ABCD是菱形
∵∠A=90°
∴ 四边形ABCD是正方形
菱形
正方形
一个角是直角
什么样的平行四边形是正方形?
正方形定义:
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
几何语言:四边形ABCD是平行四边形
∵AB=BC;∠A=90 °
∴ 四边形ABCD是正方形
归纳
正方形有什么性质?
正方形是菱形?是矩形?
正方形具有矩形的性质,同时又具有菱形的性质.
探究
正方形、菱形、矩形、平行四边形四者之间有什么关系
议一议
1.菱形,矩形,正方形都具有的性质是( )
A.对角线相等且互相平分
B.对角线相等且互相垂直平分
C.对角线互相平分
D.四条边相等,四个角相等
即时练习
C
1.如图,在正方形ABCD中,对角线AC与BD相交于点O
(1)图中是等腰三角形有:
△ABO △BOC △COD △AOD
△ABC △BCD △ACD △ABD
(2)若OA=2,你能求出BD,AB的长度吗?
2.如图,在正方形ABCD中,点F为对角线AC上一点,连接BF、DF。找出图中的全等三角形,并说明理由。
△ADF≌△ABF
△ADC≌△ABC
△DFC≌△BFC
例 如图,在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF,BE与DF之间有怎样的关系?请说明理由.
例题讲解
解: BE=DF且BE⊥DF.
理由如下:
(1)∵四边形ABCD是正方形
∴BC=DC,∠BCE=90°
∴∠DCF=180°-∠BCE=180°-90°=90°
∴∠BCE=∠DCF
又∵CE=CF
∴△BCE≌△DCF
∴BE=DF
(2)延长BE交DF于点M.
∵∠DCF=90°
∴∠CDF+∠F=90°
∴∠CBE+∠F=90°
∴∠BMF=90°
∴BE⊥DF.
1.本节课我们学习了哪些知识?
2.我们是从哪几个方面探究正方形的性质的?
3.正方形的性质有那些?
课堂小结
1.正方形面积为36,则对角线的长为( )。
检测反馈评价
习题1.7
1,2,3,4
课后作业
谢谢听讲
第一章 特殊平行四边形
1.3.1 正方形的性质
北师大版九年级上册数学
新课导入
1.几种特殊四边形的性质
2.平行四边形、菱形、矩形的定义
菱形:有一组邻边相等的平行四边形
矩形:有一个角是直角的平行四边形
3.有没有一种四边形既是菱形又是矩形呢?
对称性 边 角 对角线
平行四边形
菱形
矩形
中心对称
轴对称、中心对称
轴对称、中心对称
对边平行且相等
四边相等
对边平行且相等
对角相等;邻角互补
对角相等;邻角互补
四个角都是直角
互相平分
互相平分且垂直;平分对角
互相平分且相等
学习目标
1.在对平行四边形、矩形、菱形的认识基础上探索正方形的性质,并能运用正方形的性质进行证明与计算.
2.进一步了解平行四边形、矩形、菱形及正方形之间的相互关系.
(一)正方形的定义
探究一:矩形怎样变化后就成了正方形呢?
请用矩形纸片,通过折叠得到一个正方形。
有一组邻边相等的矩形叫做正方形.
几何语言:四边形ABCD是矩形
∵AB=BC
∴ 四边形ABCD是正方形
探究新知
矩形
正方形
一组邻边相等
探究二:菱形怎样变化后就成了正方形呢?
有一个角是直角的菱形叫做正方形.
几何语言:四边形ABCD是菱形
∵∠A=90°
∴ 四边形ABCD是正方形
菱形
正方形
一个角是直角
什么样的平行四边形是正方形?
正方形定义:
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
几何语言:四边形ABCD是平行四边形
∵AB=BC;∠A=90 °
∴ 四边形ABCD是正方形
归纳
正方形有什么性质?
正方形是菱形?是矩形?
正方形具有矩形的性质,同时又具有菱形的性质.
探究
正方形、菱形、矩形、平行四边形四者之间有什么关系
议一议
1.菱形,矩形,正方形都具有的性质是( )
A.对角线相等且互相平分
B.对角线相等且互相垂直平分
C.对角线互相平分
D.四条边相等,四个角相等
即时练习
C
1.如图,在正方形ABCD中,对角线AC与BD相交于点O
(1)图中是等腰三角形有:
△ABO △BOC △COD △AOD
△ABC △BCD △ACD △ABD
(2)若OA=2,你能求出BD,AB的长度吗?
2.如图,在正方形ABCD中,点F为对角线AC上一点,连接BF、DF。找出图中的全等三角形,并说明理由。
△ADF≌△ABF
△ADC≌△ABC
△DFC≌△BFC
例 如图,在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF,BE与DF之间有怎样的关系?请说明理由.
例题讲解
解: BE=DF且BE⊥DF.
理由如下:
(1)∵四边形ABCD是正方形
∴BC=DC,∠BCE=90°
∴∠DCF=180°-∠BCE=180°-90°=90°
∴∠BCE=∠DCF
又∵CE=CF
∴△BCE≌△DCF
∴BE=DF
(2)延长BE交DF于点M.
∵∠DCF=90°
∴∠CDF+∠F=90°
∴∠CBE+∠F=90°
∴∠BMF=90°
∴BE⊥DF.
1.本节课我们学习了哪些知识?
2.我们是从哪几个方面探究正方形的性质的?
3.正方形的性质有那些?
课堂小结
1.正方形面积为36,则对角线的长为( )。
检测反馈评价
习题1.7
1,2,3,4
课后作业
谢谢听讲
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
