24.1.2垂直于弦的直径 课件(共30张PPT)
文档属性
| 名称 | 24.1.2垂直于弦的直径 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-18 13:44:57 | ||
图片预览





文档简介
(共30张PPT)
人教版 九年级上册
24.1.2垂直于圆的直径
本课是在学生已经学习了圆的有关概念的基础上开始研究圆的性质,包括圆的轴对称性以及垂径定理,并应用垂径定理及其推论解决问题.
课件说明
学习目标:
1.理解圆的轴对称性,会运用垂径定理解决有关的
证明、计算和作图问题;
2.感受类比、转化、数形结合、方程等数学思想和
方法,在实验、观察、猜想、抽象、概括、推理
的过程中发展逻辑思维能力和识图能力.
学习重点:
垂径定理及其推论.
课件说明
由此你能得到圆的什么特性?
可以发现:圆是轴对称图形.任何一条直径所在直线都是它的对称轴.
不借助任何工具,你能找到圆形纸片的圆心吗
引入新知
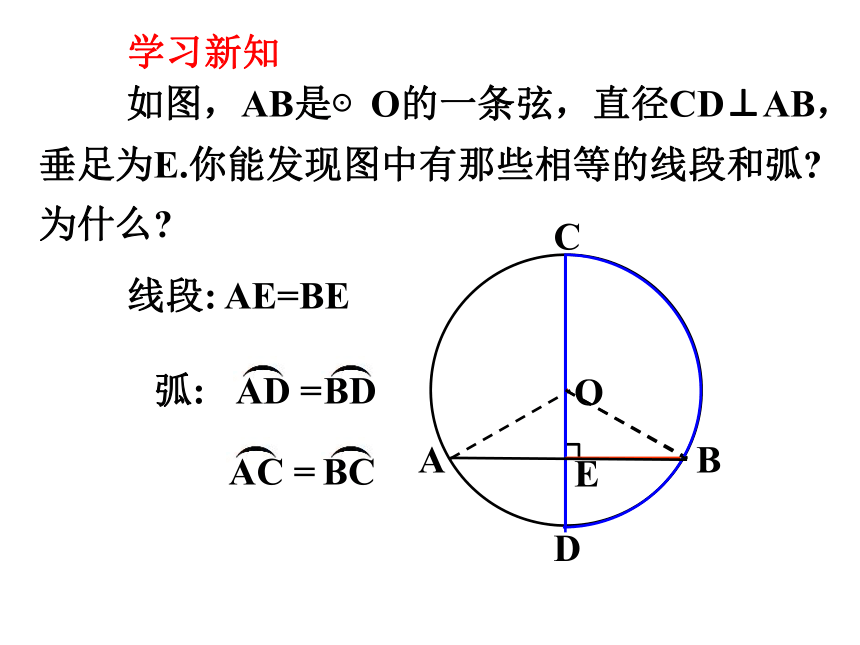
如图,AB是⊙O的一条弦,直径CD⊥AB,
垂足为E.你能发现图中有那些相等的线段和弧
为什么
·
O
A
B
C
D
E
线段: AE=BE
弧:
AD =
BD
AC =
BC
学习新知
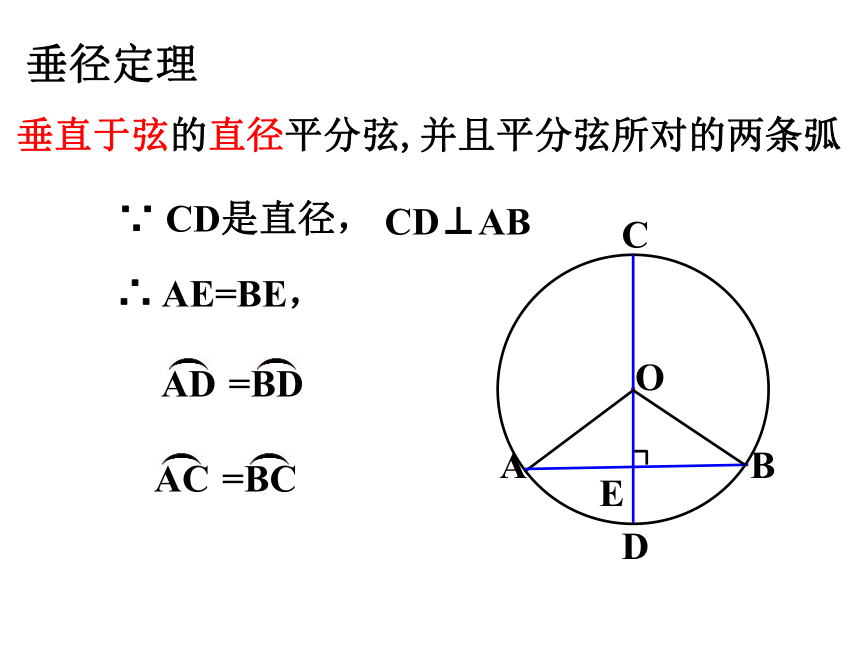
垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧
·
O
A
B
C
D
E
CD⊥AB
∴ AE=BE,
∵ CD是直径,
AD
=BD
AC
=BC
O
A
B
D
C
E
O
A
B
C
D
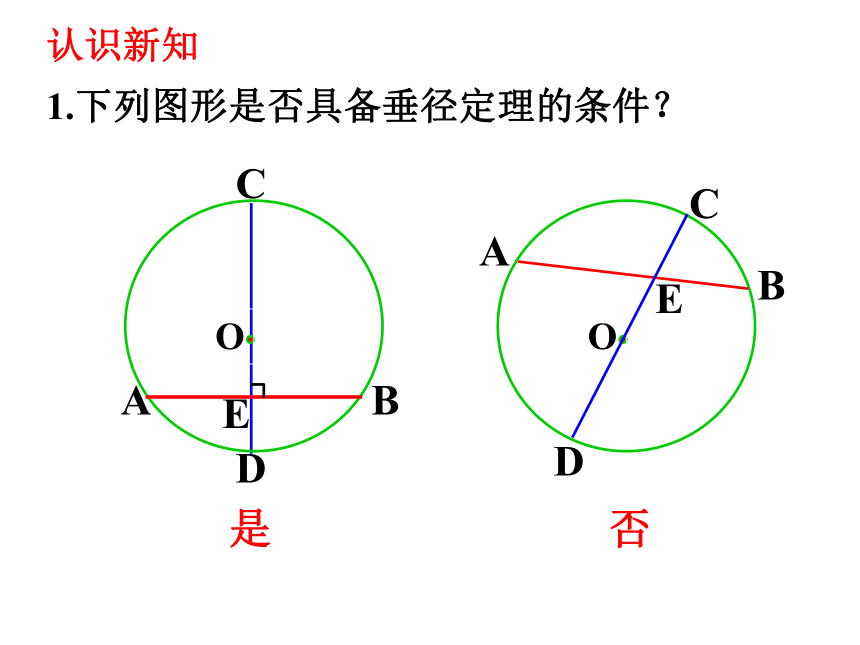
1.下列图形是否具备垂径定理的条件?
是
否
E
认识新知
O
A
B
C
E
O
A
B
C
D
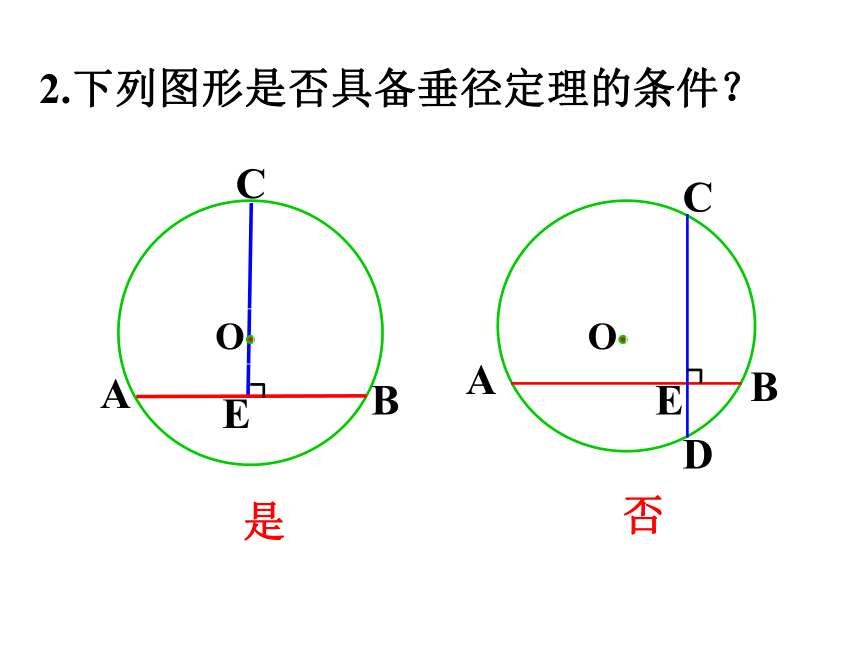
2.下列图形是否具备垂径定理的条件?
是
否
E
O
O
O
O
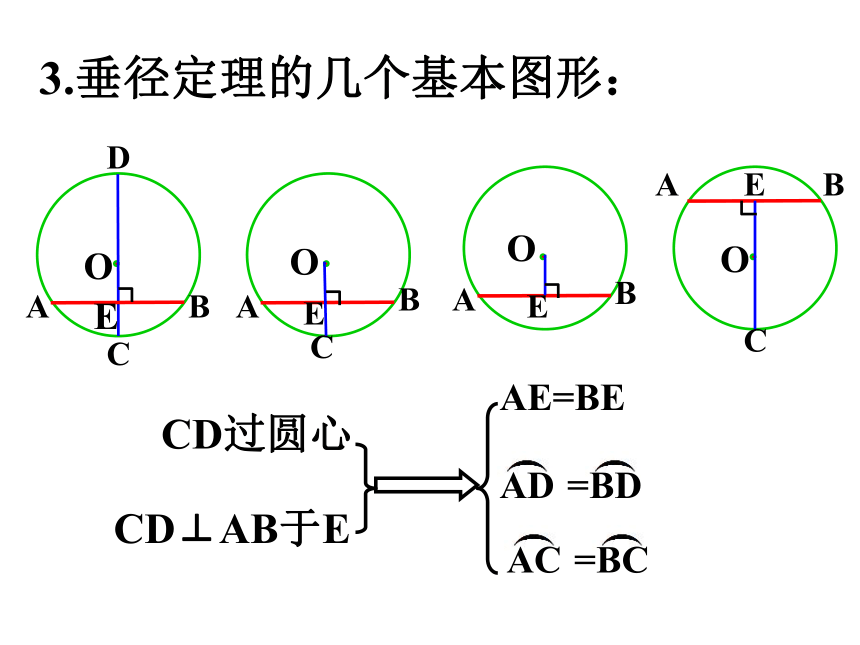
3.垂径定理的几个基本图形:
CD过圆心
CD⊥AB于E
AE=BE
A
B
A
B
C
D
E
E
C
A
B
E
A
B
C
E
AC
=BC
AD
=BD
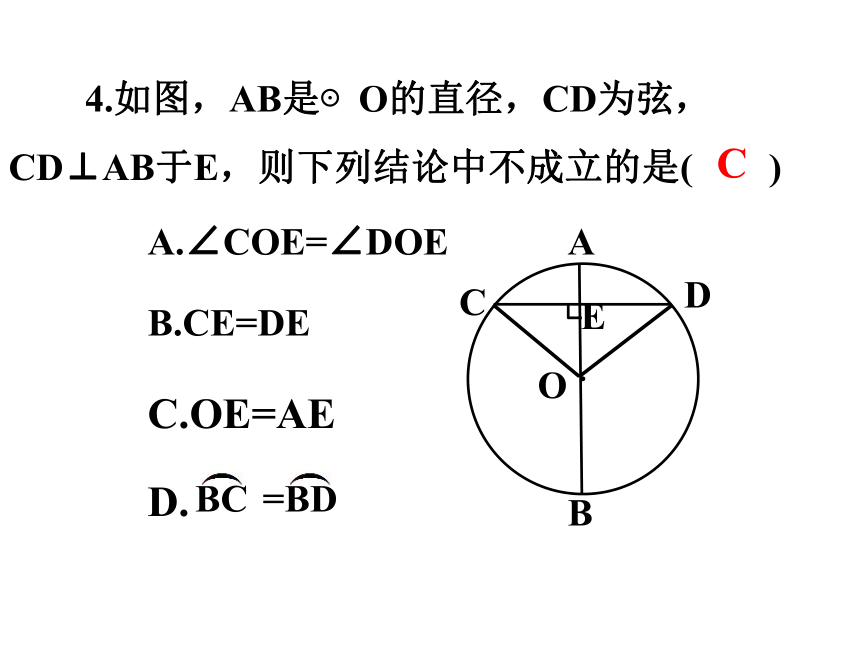
4.如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中不成立的是( )
A.∠COE=∠DOE
B.CE=DE
C.OE=AE
·
O
A
B
E
C
D
D.
C
BC
=BD
例2.如图,在⊙O中,弦AB的长为8cm,圆心O
到 AB的距离为3cm,求⊙O的半径.
·
O
A
B
E
解:过点O作OE⊥AB于E,
即⊙O的半径为5cm.
连接OA
∴AE= AB
1
2
=4cm,
OE=
3cm.
在Rt△OAE中,根据勾股定理,
OA2 =AE2+OE2
=42+32=25.
∴OA=
5cm.
典型例析
例3 如图,1 400 多年前,我国隋代建造的赵州石拱桥主桥拱是圆弧形,它的跨度(弧所对的弦长)是 37 m,拱高(弧的中点到弦的距离)为 7.23 m,求赵州桥主桥拱的半径(精确到 0.1 m).
A
B
O
解:如图,用弧AB表示主桥拱,
设弧AB所在的圆的圆心为O,半径为R.
R
37m
7.23m
A
B
O
C
D
解:如图,用弧AB表示主桥拱,设弧AB所在的圆的圆心为O,半径为R.
A
B
O
C
D
解:如图,用弧AB表示主桥拱,设弧AB所在的圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC,垂足为D,与弧AB交于点C,则D是AB的中点,C是弧AB的中点,CD就是拱高.
∴ AB=37m,CD=7.23m.
∴ AD= AB=18.5m,
∵OA2 =AD2+OD2
解得R=27.3(m).
即主桥拱半径约为27.3m.
OD=OC-CD=R-7.23
∴R2 =18.52+(R-7.23)2
1
2
A
B
O
C
关于弦的问题,常常需要过圆心作弦的垂线段,这是一条非常重要的辅助线。
圆心到弦的距离、半径、半弦构成直角三角形,便将问题转化为直角三角形的问题。
1.如图,已知在两同心圆⊙O 中,大圆弦 AB交小圆于C,D,则AC与BD间可能存在什么关系?
D
O
C
A
B
答:AC 与 BD 相等.
过点O作OE⊥AB于E,
E
理由如下:
则有:
∴AE=BE ,
CE=DE .
∴AE-CE=BE-DE ,
∴AC=BD .
学以致用
变式1
如图,连接 OA,OB,设 AO=BO,求证:AC=BD.
D
O
C
A
B
过点O作OE⊥AB于E,
则有:
∴CE=DE ,
E
∵AO=BO,
OE⊥AB,
∴AE=BE ,
∴AE-CE=BE-DE ,
∴AC=BD .
证明:
变式2
连接 OC,OD,设 OC=OD,求证:AC=BD.
D
O
C
A
B
E
过点O作OE⊥AB于E,
则有:
∴AE=BE ,
∵OC=OD,
OE⊥CD,
∴CE=DE ,
∴AE-CE=BE-DE ,
∴AC=BD .
证明:
2.如图,在⊙O中,AB、AC为互相垂直且
相等的两条弦,OD⊥AB于D,OE⊥AC于E.
求证:四边形ADOE是正方形.
D
·
O
A
B
C
E
证明:
∴四边形ADOE为矩形,
AC=AB,
∴ AE=AD,
∴ 四边形ADOE为正方形.
∵OD⊥AB,OE⊥AC,AB⊥AC,
∴∠ODA=90°,
∠OEA=90°,
∠A=90°,
∵OD= AB,
1
2
OE= AC,
1
2
1.如图,已知OC是⊙O的半径,AB是弦,OC
=5,AB=6 ,AB⊥CO于点D,则CD的长
为( ).
A. 4 B. 3 C. 2 D. 1
,
A
B
O
C
D
巩固新知
D
2.如图,AB是⊙O的直径,弦CD⊥AB于点E,
下列结论: ①CE=DE;②BE=OE;③AC=AD;
④∠CAB=∠DAB; ⑤ .一定正确
的个数有( ).
A.4个 B.3个 C.2个 D.1个
B
C
D
E
O
A
·
AD
=AC
A
3.已知⊙O的半径为13cm,弦AB//CD,AB=24cm,
CD=10cm,则AB、CD之间的距离为( ).
A.12cm B.7cm C.17cm D. 7cm或17cm
D
① 当 AB与CD在
圆心的同侧时;
②当 AB与CD在
圆心的异侧时;
O
A
B
C
D
O
A
B
C
D
EF=12-5=7
EF=12 +5=17
F
E
F
E
4.如图,⊙O的半径OA= cm,弦AB=4cm,
则圆心O到弦AB的距离为 cm.
,
A
B
O
5
1
5.如图,⊙O的直径CD⊥弦AB是于点E,且
CE=1,OB=5 ,则弦AB的长为 .
A
B
O
C
D
6
E
6.如图,一圆拱桥的拱顶到水面的距离CD为8m,
水面宽AB为8m,则拱桥的OC长为 .
OD2+AD2=OA2
(8-OC)2+42=OC2
64-16OC+OC2+16=OC2
OC=5
5m
A
B
O
C
D
内容:
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
①构造直角三角形,垂径定理和勾股定理有机结合是计算弦长、半径和弦心距等问题的方法.
②技巧:重要辅助线是过圆心作弦的垂线.
重要思路:(由)垂径定理—构造直角三角形—
(结合)勾股定理—建立方程.
小结
今天作业
课本P89页第2题
课本P83页第2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 九年级上册
24.1.2垂直于圆的直径
本课是在学生已经学习了圆的有关概念的基础上开始研究圆的性质,包括圆的轴对称性以及垂径定理,并应用垂径定理及其推论解决问题.
课件说明
学习目标:
1.理解圆的轴对称性,会运用垂径定理解决有关的
证明、计算和作图问题;
2.感受类比、转化、数形结合、方程等数学思想和
方法,在实验、观察、猜想、抽象、概括、推理
的过程中发展逻辑思维能力和识图能力.
学习重点:
垂径定理及其推论.
课件说明
由此你能得到圆的什么特性?
可以发现:圆是轴对称图形.任何一条直径所在直线都是它的对称轴.
不借助任何工具,你能找到圆形纸片的圆心吗
引入新知
如图,AB是⊙O的一条弦,直径CD⊥AB,
垂足为E.你能发现图中有那些相等的线段和弧
为什么
·
O
A
B
C
D
E
线段: AE=BE
弧:
AD =
BD
AC =
BC
学习新知
垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧
·
O
A
B
C
D
E
CD⊥AB
∴ AE=BE,
∵ CD是直径,
AD
=BD
AC
=BC
O
A
B
D
C
E
O
A
B
C
D
1.下列图形是否具备垂径定理的条件?
是
否
E
认识新知
O
A
B
C
E
O
A
B
C
D
2.下列图形是否具备垂径定理的条件?
是
否
E
O
O
O
O
3.垂径定理的几个基本图形:
CD过圆心
CD⊥AB于E
AE=BE
A
B
A
B
C
D
E
E
C
A
B
E
A
B
C
E
AC
=BC
AD
=BD
4.如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中不成立的是( )
A.∠COE=∠DOE
B.CE=DE
C.OE=AE
·
O
A
B
E
C
D
D.
C
BC
=BD
例2.如图,在⊙O中,弦AB的长为8cm,圆心O
到 AB的距离为3cm,求⊙O的半径.
·
O
A
B
E
解:过点O作OE⊥AB于E,
即⊙O的半径为5cm.
连接OA
∴AE= AB
1
2
=4cm,
OE=
3cm.
在Rt△OAE中,根据勾股定理,
OA2 =AE2+OE2
=42+32=25.
∴OA=
5cm.
典型例析
例3 如图,1 400 多年前,我国隋代建造的赵州石拱桥主桥拱是圆弧形,它的跨度(弧所对的弦长)是 37 m,拱高(弧的中点到弦的距离)为 7.23 m,求赵州桥主桥拱的半径(精确到 0.1 m).
A
B
O
解:如图,用弧AB表示主桥拱,
设弧AB所在的圆的圆心为O,半径为R.
R
37m
7.23m
A
B
O
C
D
解:如图,用弧AB表示主桥拱,设弧AB所在的圆的圆心为O,半径为R.
A
B
O
C
D
解:如图,用弧AB表示主桥拱,设弧AB所在的圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC,垂足为D,与弧AB交于点C,则D是AB的中点,C是弧AB的中点,CD就是拱高.
∴ AB=37m,CD=7.23m.
∴ AD= AB=18.5m,
∵OA2 =AD2+OD2
解得R=27.3(m).
即主桥拱半径约为27.3m.
OD=OC-CD=R-7.23
∴R2 =18.52+(R-7.23)2
1
2
A
B
O
C
关于弦的问题,常常需要过圆心作弦的垂线段,这是一条非常重要的辅助线。
圆心到弦的距离、半径、半弦构成直角三角形,便将问题转化为直角三角形的问题。
1.如图,已知在两同心圆⊙O 中,大圆弦 AB交小圆于C,D,则AC与BD间可能存在什么关系?
D
O
C
A
B
答:AC 与 BD 相等.
过点O作OE⊥AB于E,
E
理由如下:
则有:
∴AE=BE ,
CE=DE .
∴AE-CE=BE-DE ,
∴AC=BD .
学以致用
变式1
如图,连接 OA,OB,设 AO=BO,求证:AC=BD.
D
O
C
A
B
过点O作OE⊥AB于E,
则有:
∴CE=DE ,
E
∵AO=BO,
OE⊥AB,
∴AE=BE ,
∴AE-CE=BE-DE ,
∴AC=BD .
证明:
变式2
连接 OC,OD,设 OC=OD,求证:AC=BD.
D
O
C
A
B
E
过点O作OE⊥AB于E,
则有:
∴AE=BE ,
∵OC=OD,
OE⊥CD,
∴CE=DE ,
∴AE-CE=BE-DE ,
∴AC=BD .
证明:
2.如图,在⊙O中,AB、AC为互相垂直且
相等的两条弦,OD⊥AB于D,OE⊥AC于E.
求证:四边形ADOE是正方形.
D
·
O
A
B
C
E
证明:
∴四边形ADOE为矩形,
AC=AB,
∴ AE=AD,
∴ 四边形ADOE为正方形.
∵OD⊥AB,OE⊥AC,AB⊥AC,
∴∠ODA=90°,
∠OEA=90°,
∠A=90°,
∵OD= AB,
1
2
OE= AC,
1
2
1.如图,已知OC是⊙O的半径,AB是弦,OC
=5,AB=6 ,AB⊥CO于点D,则CD的长
为( ).
A. 4 B. 3 C. 2 D. 1
,
A
B
O
C
D
巩固新知
D
2.如图,AB是⊙O的直径,弦CD⊥AB于点E,
下列结论: ①CE=DE;②BE=OE;③AC=AD;
④∠CAB=∠DAB; ⑤ .一定正确
的个数有( ).
A.4个 B.3个 C.2个 D.1个
B
C
D
E
O
A
·
AD
=AC
A
3.已知⊙O的半径为13cm,弦AB//CD,AB=24cm,
CD=10cm,则AB、CD之间的距离为( ).
A.12cm B.7cm C.17cm D. 7cm或17cm
D
① 当 AB与CD在
圆心的同侧时;
②当 AB与CD在
圆心的异侧时;
O
A
B
C
D
O
A
B
C
D
EF=12-5=7
EF=12 +5=17
F
E
F
E
4.如图,⊙O的半径OA= cm,弦AB=4cm,
则圆心O到弦AB的距离为 cm.
,
A
B
O
5
1
5.如图,⊙O的直径CD⊥弦AB是于点E,且
CE=1,OB=5 ,则弦AB的长为 .
A
B
O
C
D
6
E
6.如图,一圆拱桥的拱顶到水面的距离CD为8m,
水面宽AB为8m,则拱桥的OC长为 .
OD2+AD2=OA2
(8-OC)2+42=OC2
64-16OC+OC2+16=OC2
OC=5
5m
A
B
O
C
D
内容:
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
①构造直角三角形,垂径定理和勾股定理有机结合是计算弦长、半径和弦心距等问题的方法.
②技巧:重要辅助线是过圆心作弦的垂线.
重要思路:(由)垂径定理—构造直角三角形—
(结合)勾股定理—建立方程.
小结
今天作业
课本P89页第2题
课本P83页第2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
