24.1.3弧、弦、圆心角 课件(共28张PPT)
文档属性
| 名称 | 24.1.3弧、弦、圆心角 课件(共28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-18 13:48:02 | ||
图片预览



文档简介
(共28张PPT)
人教版 九年级上册
24.1.3 弧、弦、圆心角
本节课是在学习了垂径定理后,进而学习圆的又一个重要性质,主要研究弧,弦,圆心角的关系.
课件说明
学习目标: 1.了解圆心角的概念; 2.掌握在同圆或等圆中,两个圆心角、两条弧、两 条弦中有一组量相等,就可以推出它们所对应的 其余各组量也相等.
学习重点: 同圆或等圆中弧、弦、圆心角之间的关系.
课件说明
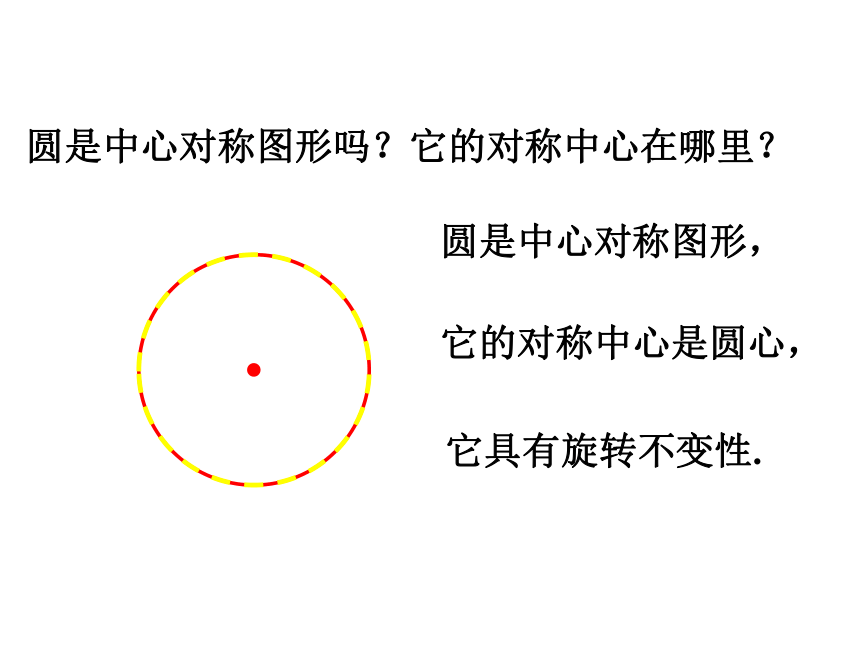
圆是中心对称图形吗?它的对称中心在哪里?
·
圆是中心对称图形,
它的对称中心是圆心,
它具有旋转不变性.
·
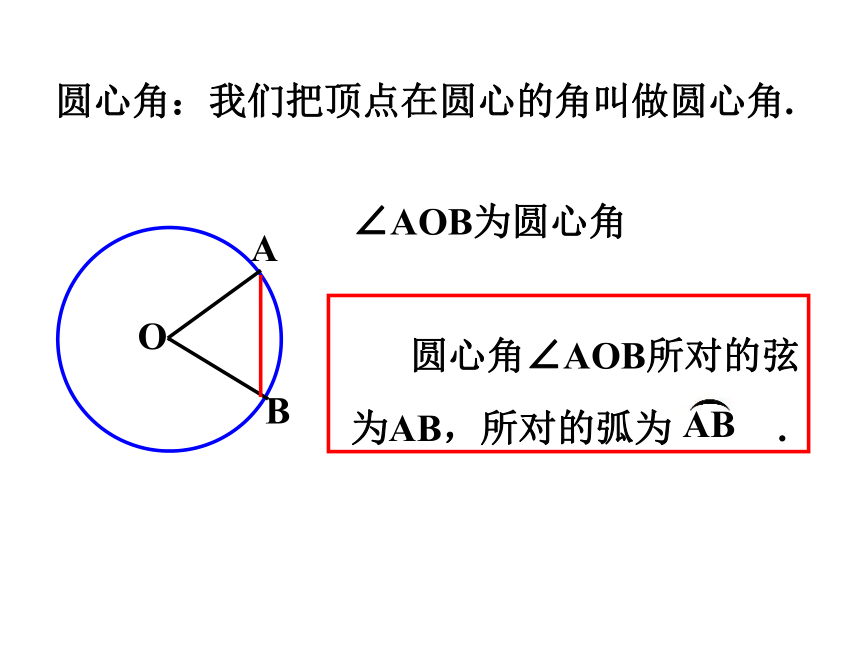
圆心角:我们把顶点在圆心的角叫做圆心角.
O
B
A
∠AOB为圆心角
圆心角∠AOB所对的弦为AB,所对的弧为 .
AB
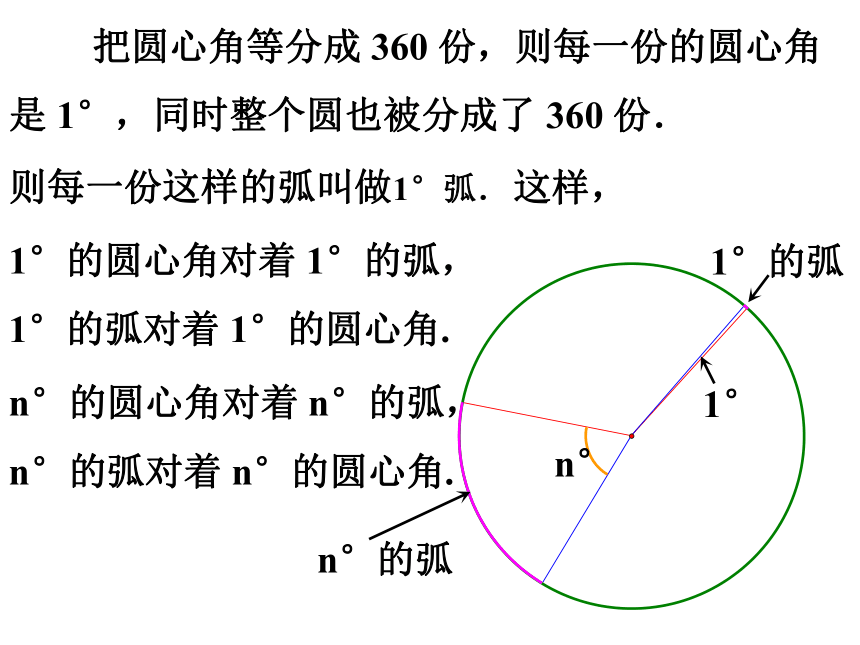
把圆心角等分成 360 份,则每一份的圆心角是 1°,同时整个圆也被分成了 360 份.
则每一份这样的弧叫做1°弧.
1°的圆心角对着 1°的弧, 1°的弧对着 1°的圆心角.
这样,
1°的弧
1°
n°的弧
n°
n°的圆心角对着 n°的弧, n°的弧对着 n°的圆心角.
1°的弧
1°
n°的弧
n°
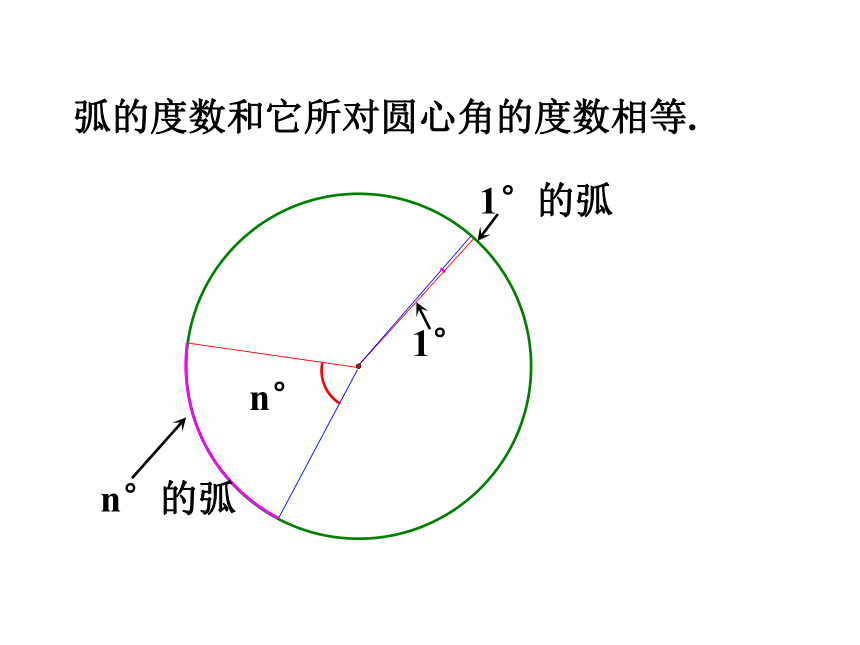
弧的度数和它所对圆心角的度数相等.
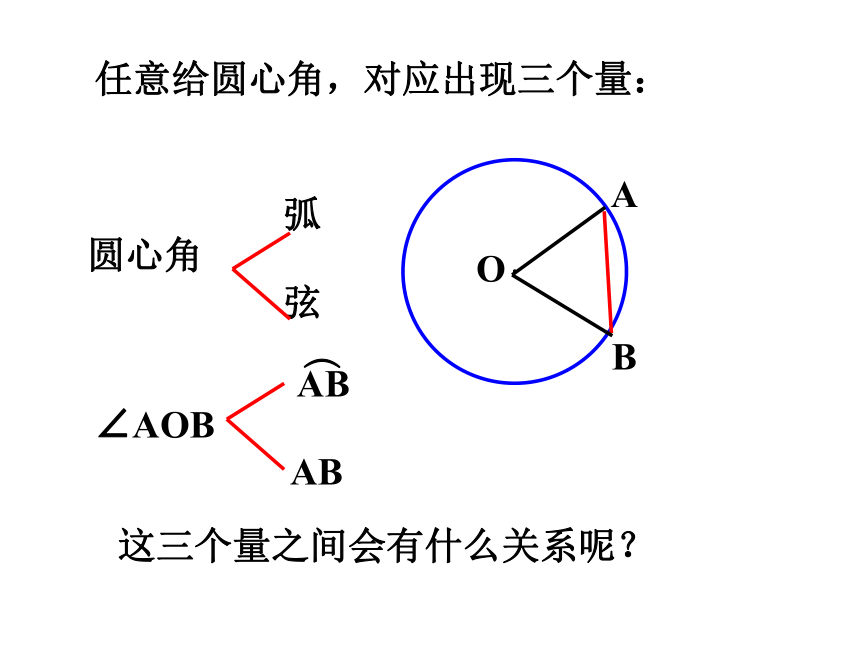
任意给圆心角,对应出现三个量:
圆心角
弧
弦
·
O
B
A
这三个量之间会有什么关系呢?
∠AOB
AB
AB
︵
·
O
A
B
A1
B1
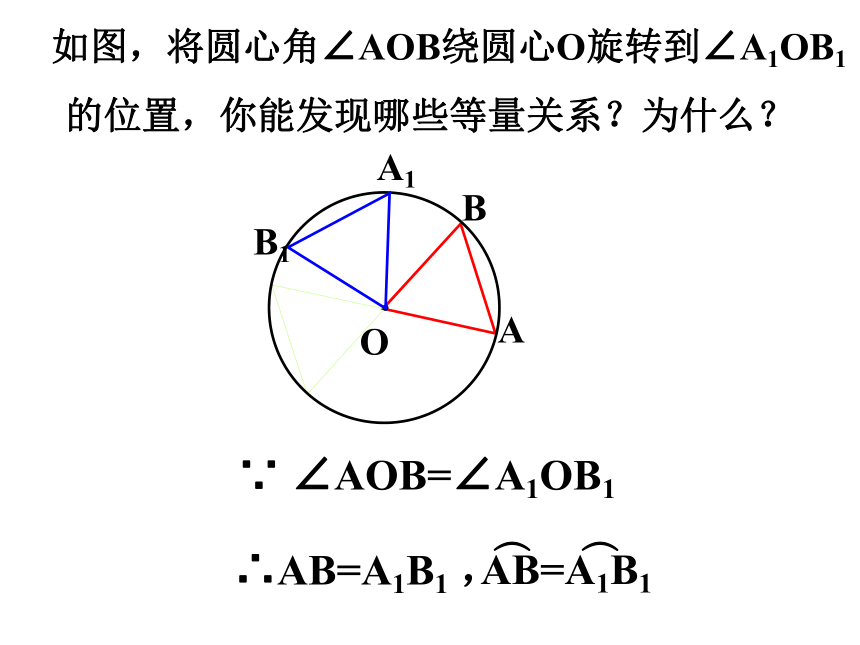
∵ ∠AOB=∠A1OB1
∴AB=A1B1 ,
如图,将圆心角∠AOB绕圆心O旋转到∠A1OB1的位置,你能发现哪些等量关系?为什么?
AB=A1B1
︵
︵
O
α
A
B
A1
B1
α
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
圆心角定理
同样,还可以得到:
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角______ , 所对的弦______;
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角______,所对的弧______.
相等
相等
相等
相等
O
α
A
B
A1
B1
α
同圆或等圆中,两个圆心角、两条圆心角所对的弧、两条圆心角所对的弦中如果有一组量相等,它们所对应的其余各组量也相等。
O
B
C
A
∴AB=AC.
∵∠ACB=60°,
∴△ABC是等边三角形,
∴AB=BC=CA,
∴∠AOB=∠BOC=∠AOC.
例1 如图,在⊙O中,AB=AC,∠ACB=60°, 求证:∠AOB=∠BOC=∠AOC.
︵
︵
例题解析
证明:
︵
︵
∵AB=AC,
1.如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么 , .
(2)如果 ,那么 , .
(3)如果∠AOB=∠COD,那么 , .
(4)如果AB=CD,OE⊥AB于E,
OF⊥CD于F,OE与OF相等吗?
为什么?
A
B
C
D
E
F
O
认识新知
AB=CD
︵
︵
∠AOB=∠COD
AB=CD
︵
︵
AB=CD
∠AOB=∠COD
AB=CD
AB=CD
︵
︵
OE=OF
全等三角形对应边上的高相等
2.如图,AB是⊙O的直径,BC=CD=DE,∠COD=35°,求∠AOE的度数.
O
A
B
E
D
C
证明: ∵ BC=CD=DE
∴∠COB=∠COD=∠DOE=35°
∴∠AOE=180°-∠COB-∠COD-∠DOE
=75°
︵
︵
︵
︵
︵
︵
3.如图,AD=BC,那么比较AB与CD的大小.
O
D
C
A
B
解: ∵AD=BC,
∴AD=BC.
∴AD+AC=BC+AC,
∴AB=CD.
︵
︵
︵
︵
︵
︵
︵
︵
︵
︵
4.如图,在⊙O 中,弦 AB 所对的劣弧为圆的
,圆的半径为 4 cm,求 AB 的长.
A
B
O
∵弦 AB 所对的劣弧为圆的 ,
解:
∴AB=120°,
∴∠AOB=120°.
∵ OA=OB,
∴∠A=30°.
过点O作OE⊥AB于E,
∴OE=2.
∵ OA=4,
∴AE=
∴AB=2AE
=
E
OA2-OE2
=
42-22
=
3
2
3
4
(cm).
1
3
1
3
︵
1.如图,在⊙O中,AB=AC,∠AOB=120°,
则∠AOC的度数为( ).
A.122° B.120° C.61° D.58°
︵
︵
O
A
B
C
B
巩固新知
2.如图,在⊙O中,AC=BC,∠A=50°,
则∠BOC的度数为( ).
A.40° B.45° C.50° D.60°
︵
︵
O
A
B
C
A
3.如图,AB是⊙O的直径,BC=CD=DE,
∠COD=34°,则∠AEO的度数为( ).
A.51° B.56° C.68° D.78°
︵
︵
︵
O
A
B
E
D
C
A
O
A
B
D
C
B
4.如图,圆心角∠AOB=20°,将AB绕圆心O
旋转得到CD,则CD的度数是( ).
A.n° B.20° C.20°+n° D.40°+ n°
︵
︵
︵
5.如图,AB是⊙O的直径,点C是BD的中点,
∠BOD=120°,AC交OD于点E,DE=1,
则AE的长为( ).
A. B. C. D.
︵
O
A
B
E
D
C
A
5
2
3
2
5
3
6.如图,在⊙O中,AB=AC,AB=3,则AC= .
︵
︵
O
A
B
C
3
7.如图,AB和DE是⊙O的直径,弦AC∥ DE,
若弦BE=5,则弦CE= .
O
A
B
E
D
C
5
(1)本节课学习了哪些内容?
(2)圆心角、弧、弦之间有哪些关系?
小结
今天作业
课本P89页第3、4题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 九年级上册
24.1.3 弧、弦、圆心角
本节课是在学习了垂径定理后,进而学习圆的又一个重要性质,主要研究弧,弦,圆心角的关系.
课件说明
学习目标: 1.了解圆心角的概念; 2.掌握在同圆或等圆中,两个圆心角、两条弧、两 条弦中有一组量相等,就可以推出它们所对应的 其余各组量也相等.
学习重点: 同圆或等圆中弧、弦、圆心角之间的关系.
课件说明
圆是中心对称图形吗?它的对称中心在哪里?
·
圆是中心对称图形,
它的对称中心是圆心,
它具有旋转不变性.
·
圆心角:我们把顶点在圆心的角叫做圆心角.
O
B
A
∠AOB为圆心角
圆心角∠AOB所对的弦为AB,所对的弧为 .
AB
把圆心角等分成 360 份,则每一份的圆心角是 1°,同时整个圆也被分成了 360 份.
则每一份这样的弧叫做1°弧.
1°的圆心角对着 1°的弧, 1°的弧对着 1°的圆心角.
这样,
1°的弧
1°
n°的弧
n°
n°的圆心角对着 n°的弧, n°的弧对着 n°的圆心角.
1°的弧
1°
n°的弧
n°
弧的度数和它所对圆心角的度数相等.
任意给圆心角,对应出现三个量:
圆心角
弧
弦
·
O
B
A
这三个量之间会有什么关系呢?
∠AOB
AB
AB
︵
·
O
A
B
A1
B1
∵ ∠AOB=∠A1OB1
∴AB=A1B1 ,
如图,将圆心角∠AOB绕圆心O旋转到∠A1OB1的位置,你能发现哪些等量关系?为什么?
AB=A1B1
︵
︵
O
α
A
B
A1
B1
α
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
圆心角定理
同样,还可以得到:
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角______ , 所对的弦______;
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角______,所对的弧______.
相等
相等
相等
相等
O
α
A
B
A1
B1
α
同圆或等圆中,两个圆心角、两条圆心角所对的弧、两条圆心角所对的弦中如果有一组量相等,它们所对应的其余各组量也相等。
O
B
C
A
∴AB=AC.
∵∠ACB=60°,
∴△ABC是等边三角形,
∴AB=BC=CA,
∴∠AOB=∠BOC=∠AOC.
例1 如图,在⊙O中,AB=AC,∠ACB=60°, 求证:∠AOB=∠BOC=∠AOC.
︵
︵
例题解析
证明:
︵
︵
∵AB=AC,
1.如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么 , .
(2)如果 ,那么 , .
(3)如果∠AOB=∠COD,那么 , .
(4)如果AB=CD,OE⊥AB于E,
OF⊥CD于F,OE与OF相等吗?
为什么?
A
B
C
D
E
F
O
认识新知
AB=CD
︵
︵
∠AOB=∠COD
AB=CD
︵
︵
AB=CD
∠AOB=∠COD
AB=CD
AB=CD
︵
︵
OE=OF
全等三角形对应边上的高相等
2.如图,AB是⊙O的直径,BC=CD=DE,∠COD=35°,求∠AOE的度数.
O
A
B
E
D
C
证明: ∵ BC=CD=DE
∴∠COB=∠COD=∠DOE=35°
∴∠AOE=180°-∠COB-∠COD-∠DOE
=75°
︵
︵
︵
︵
︵
︵
3.如图,AD=BC,那么比较AB与CD的大小.
O
D
C
A
B
解: ∵AD=BC,
∴AD=BC.
∴AD+AC=BC+AC,
∴AB=CD.
︵
︵
︵
︵
︵
︵
︵
︵
︵
︵
4.如图,在⊙O 中,弦 AB 所对的劣弧为圆的
,圆的半径为 4 cm,求 AB 的长.
A
B
O
∵弦 AB 所对的劣弧为圆的 ,
解:
∴AB=120°,
∴∠AOB=120°.
∵ OA=OB,
∴∠A=30°.
过点O作OE⊥AB于E,
∴OE=2.
∵ OA=4,
∴AE=
∴AB=2AE
=
E
OA2-OE2
=
42-22
=
3
2
3
4
(cm).
1
3
1
3
︵
1.如图,在⊙O中,AB=AC,∠AOB=120°,
则∠AOC的度数为( ).
A.122° B.120° C.61° D.58°
︵
︵
O
A
B
C
B
巩固新知
2.如图,在⊙O中,AC=BC,∠A=50°,
则∠BOC的度数为( ).
A.40° B.45° C.50° D.60°
︵
︵
O
A
B
C
A
3.如图,AB是⊙O的直径,BC=CD=DE,
∠COD=34°,则∠AEO的度数为( ).
A.51° B.56° C.68° D.78°
︵
︵
︵
O
A
B
E
D
C
A
O
A
B
D
C
B
4.如图,圆心角∠AOB=20°,将AB绕圆心O
旋转得到CD,则CD的度数是( ).
A.n° B.20° C.20°+n° D.40°+ n°
︵
︵
︵
5.如图,AB是⊙O的直径,点C是BD的中点,
∠BOD=120°,AC交OD于点E,DE=1,
则AE的长为( ).
A. B. C. D.
︵
O
A
B
E
D
C
A
5
2
3
2
5
3
6.如图,在⊙O中,AB=AC,AB=3,则AC= .
︵
︵
O
A
B
C
3
7.如图,AB和DE是⊙O的直径,弦AC∥ DE,
若弦BE=5,则弦CE= .
O
A
B
E
D
C
5
(1)本节课学习了哪些内容?
(2)圆心角、弧、弦之间有哪些关系?
小结
今天作业
课本P89页第3、4题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
