北师大版八年级下册 3.3 中心对称 课件(共19张PPT)
文档属性
| 名称 | 北师大版八年级下册 3.3 中心对称 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 434.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-18 20:56:35 | ||
图片预览





文档简介
(共19张PPT)
第3章 图形的平移与旋转
3.3 中心对称
引入课题
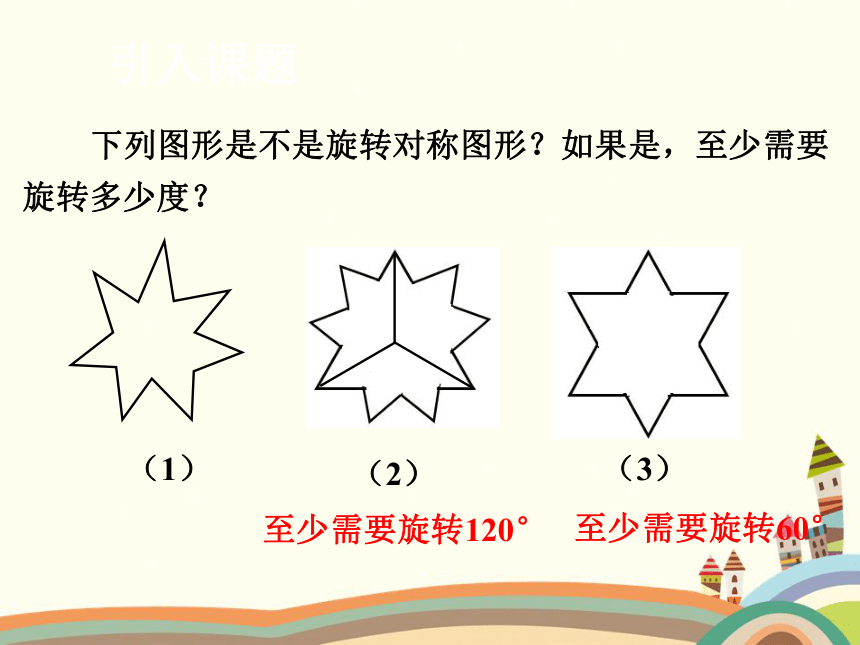
下列图形是不是旋转对称图形?如果是,至少需要旋转多少度?
至少需要旋转120°
(1)
(2)
(3)
至少需要旋转60°
探究新知
中心对称:如果把一个图形绕着某一点旋转180°,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做它们的对称中心.
探究新知
观察下图,图(1)和图(2)两个图形成中心对称吗?对称中心在哪里?
(1)
(2)
成中心对称,
对称中心为O点
O
探究新知
观察下图,图(1)和图(2)两个图形成中心对称吗?对称中心在哪里?
(1)
(2)
成中心对称,
对称中心为O点
O
探究新知
对称中心的含义是:
①两个图形能够完全重合;②重合方式有限制,不是把一个图形平移到另一个图形上面,也不是沿一条直线对折,而是把一个图形绕着某一点旋转180°之后与另一个图形重合.
由此可见成中心对称的图形一定全等,而全等的图形不一定成中心对称.
探究新知
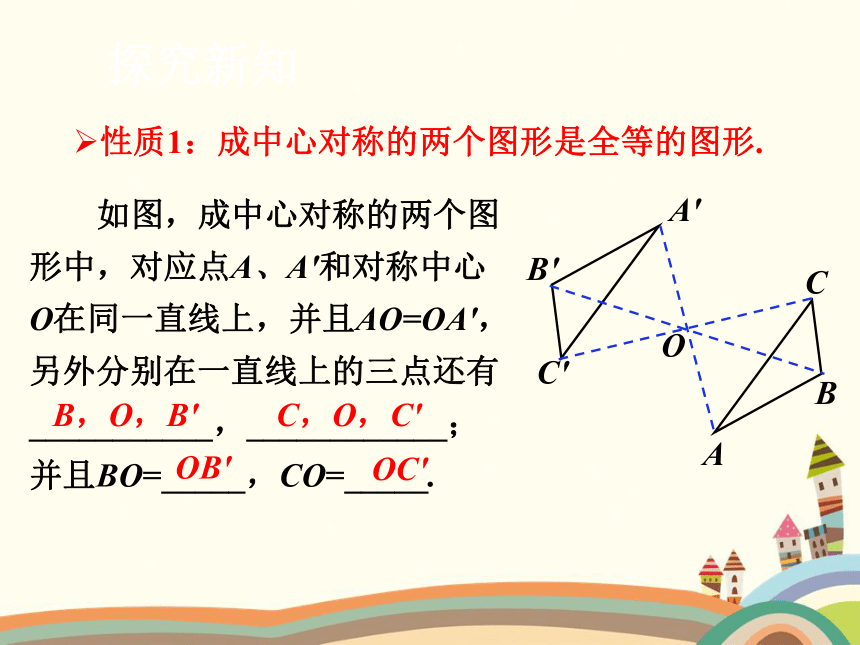
性质1:成中心对称的两个图形是全等的图形.
如图,成中心对称的两个图形中,对应点A、A′和对称中心O在同一直线上,并且AO=OA′,另外分别在一直线上的三点还有___________,____________;并且BO=_____,CO=_____.
A
B
C
A′
B′
C′
O
B,O,B′
OC′
OB′
C,O,C′
探究新知
性质2:成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.
也就是: ①对称中心在任意两个对应点的连线上.
②对称中心到一对对应点的距离相等.
根据这个性质,可以找到成中心对称的两个图形的对称中心,通常只需连接两个图形上的一对对应点,所得线段的中点就是对称中心.同时在证明线段相等时也有应用.
③中心对称的识别.
反过来说,如果两个图形的对应点所连的线段都经过某一点,且被平分,那么这两个图形一定关于这一点成中心对称.
下面哪个图形是中心对称图形?
探究新知
探究新知
中心对称图形的概念:把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
下图是一幅中心对称图形,请你找出点A绕点O旋转180°后的对应点B,及点C的对应点D.你是怎么找的?
探究新知
A
E
O
C
B
D
现在你能很快地找出点E的对应点F吗?
F
你能发现中心对称图形上的一对对应点与对称中心的关系吗?
探究新知
中心对称图形上的一对对应点经过对称中心.
探究新知
讨论:
(1)三角形是中心对称图形吗?
(2)正五边形是中心对称图形吗?
(3)正六边形是中心对称图形吗?
(4)除了平行四边形,你还能找到哪些多边形是中心对称图形?
边数为偶数的正多边形都是中心对称图形.
不是
不是
是
轴对称图形 中心对称图形
探究新知
轴对称图形与中心对称图形有何不同,你能列表得出吗?
有一条对称轴——直线
有一个对称中心——点
沿对称轴对折
绕对称中心旋转180°
对折后与原图形重合
旋转后与原图形重合
探究新知
1.在数字0至9中,哪些是中心对称图形?
0,1,8
探究新知
2.世界上因为有了圆的图案,万物才显得富有生机,以下来自现实生活的图形中都有圆,它们看上去是那么美丽与和谐,这正是因为圆具有轴对称和中心对称性.请问以下三个图形中是轴对称图形的有______,是中心对称图形的有______.
(1)(2)(3)
(1)一石激起千层浪
(2)方向盘
(3)铜钱
(1)(3)
课堂小结
本节课学了哪些知识?
布置作业
教材习题3.6.
谢谢大家!
再见!
第3章 图形的平移与旋转
3.3 中心对称
引入课题
下列图形是不是旋转对称图形?如果是,至少需要旋转多少度?
至少需要旋转120°
(1)
(2)
(3)
至少需要旋转60°
探究新知
中心对称:如果把一个图形绕着某一点旋转180°,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做它们的对称中心.
探究新知
观察下图,图(1)和图(2)两个图形成中心对称吗?对称中心在哪里?
(1)
(2)
成中心对称,
对称中心为O点
O
探究新知
观察下图,图(1)和图(2)两个图形成中心对称吗?对称中心在哪里?
(1)
(2)
成中心对称,
对称中心为O点
O
探究新知
对称中心的含义是:
①两个图形能够完全重合;②重合方式有限制,不是把一个图形平移到另一个图形上面,也不是沿一条直线对折,而是把一个图形绕着某一点旋转180°之后与另一个图形重合.
由此可见成中心对称的图形一定全等,而全等的图形不一定成中心对称.
探究新知
性质1:成中心对称的两个图形是全等的图形.
如图,成中心对称的两个图形中,对应点A、A′和对称中心O在同一直线上,并且AO=OA′,另外分别在一直线上的三点还有___________,____________;并且BO=_____,CO=_____.
A
B
C
A′
B′
C′
O
B,O,B′
OC′
OB′
C,O,C′
探究新知
性质2:成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.
也就是: ①对称中心在任意两个对应点的连线上.
②对称中心到一对对应点的距离相等.
根据这个性质,可以找到成中心对称的两个图形的对称中心,通常只需连接两个图形上的一对对应点,所得线段的中点就是对称中心.同时在证明线段相等时也有应用.
③中心对称的识别.
反过来说,如果两个图形的对应点所连的线段都经过某一点,且被平分,那么这两个图形一定关于这一点成中心对称.
下面哪个图形是中心对称图形?
探究新知
探究新知
中心对称图形的概念:把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
下图是一幅中心对称图形,请你找出点A绕点O旋转180°后的对应点B,及点C的对应点D.你是怎么找的?
探究新知
A
E
O
C
B
D
现在你能很快地找出点E的对应点F吗?
F
你能发现中心对称图形上的一对对应点与对称中心的关系吗?
探究新知
中心对称图形上的一对对应点经过对称中心.
探究新知
讨论:
(1)三角形是中心对称图形吗?
(2)正五边形是中心对称图形吗?
(3)正六边形是中心对称图形吗?
(4)除了平行四边形,你还能找到哪些多边形是中心对称图形?
边数为偶数的正多边形都是中心对称图形.
不是
不是
是
轴对称图形 中心对称图形
探究新知
轴对称图形与中心对称图形有何不同,你能列表得出吗?
有一条对称轴——直线
有一个对称中心——点
沿对称轴对折
绕对称中心旋转180°
对折后与原图形重合
旋转后与原图形重合
探究新知
1.在数字0至9中,哪些是中心对称图形?
0,1,8
探究新知
2.世界上因为有了圆的图案,万物才显得富有生机,以下来自现实生活的图形中都有圆,它们看上去是那么美丽与和谐,这正是因为圆具有轴对称和中心对称性.请问以下三个图形中是轴对称图形的有______,是中心对称图形的有______.
(1)(2)(3)
(1)一石激起千层浪
(2)方向盘
(3)铜钱
(1)(3)
课堂小结
本节课学了哪些知识?
布置作业
教材习题3.6.
谢谢大家!
再见!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
