沪科版八年级下册19.3.2 矩形的性质与判定课件(共17张PPT)
文档属性
| 名称 | 沪科版八年级下册19.3.2 矩形的性质与判定课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 137.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-19 08:48:50 | ||
图片预览





文档简介
(共17张PPT)
第十九章 特殊平行四边形
19.2.2、矩形的性质与判定
第一步:交流预习
环节1:教师提问
O
D
C
B
A
一、什么叫矩形?矩形有哪些性质?
二、填空
1、矩形具有而一般的平行四边形不具有的性质是( )
A.对角相等 B.对边平行且相等
C.对角线相等 D.对角线互相平分
2、下列性质中,矩形不一定具有的是( ) A.是中心对称图形 B.四个角都相等
C.是轴对称图形 D.对角线互相垂直
C
D
第一步:交流预习
1、回答14页和15页“做一做”和“想一想” 提出的问题,并猜想矩形有哪些判定方法?你会证明你的猜想吗?
2、回答15页“议一议”提出的问题,仅有绳子,你是怎样检查门框是矩形的?
3、自学15页例2,并指
出每一步的理由。
O
D
C
B
A
环节2:师友交流
请把你预习中的疑惑与师傅交流
第二步:互助探究
环节1:师友探究
矩形还有哪些判定方法?请说出你的猜想?
猜想1:对角线相等的平行四边形是矩形
猜想2:有三个角是直角的四边形是矩形.
矩形的定义:
有一个角是直角的平行四边形是矩形。
探究矩形的判定
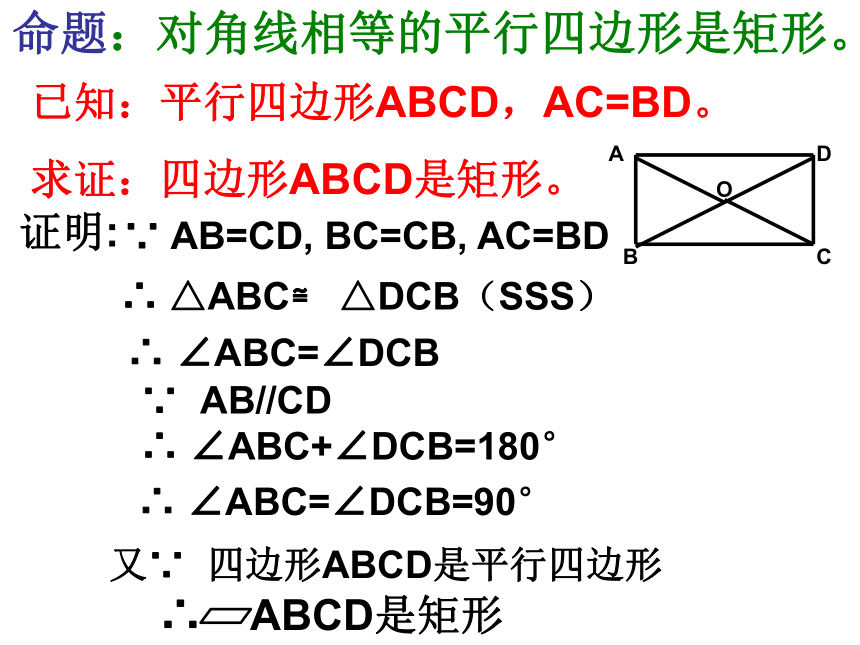
命题:对角线相等的平行四边形是矩形。
已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。
证明:
∵ AB=CD, BC=CB, AC=BD
∴ △ABC≌ △DCB(SSS)
∵ AB//CD
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=∠DCB=90°
∴ ∠ABC=∠DCB
∴ ABCD是矩形
O
D
C
B
A
又∵ 四边形ABCD是平行四边形
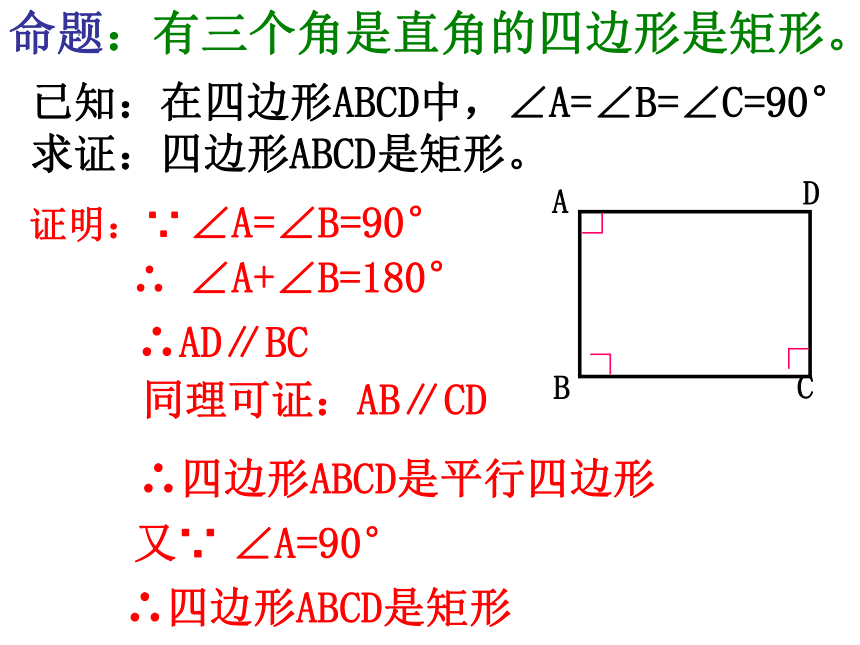
已知:在四边形ABCD中,∠A=∠B=∠C=90°
求证:四边形ABCD是矩形。
A
B
C
D
∟
∟
∟
证明:∵ ∠A=∠B=90°
∴ ∠A+∠B=180°
∴AD∥BC
同理可证:AB∥CD
∴四边形ABCD是平行四边形
又∵ ∠A=90°
∴四边形ABCD是矩形
命题:有三个角是直角的四边形是矩形。
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
矩形的判定方法:
定义:
定理:
定理:
如果四边形ABCD的对角线AC=BD,这样的四边形是不是矩形
A
B
C
D
AC=BD
A
B
C
D
AC=BD
都不是矩形
想一想
18 七月 2022
情境:仅有一根绳子,你能检查窗框是否是矩形吗?你是怎样检查的?
第二步:互助探究
环节1:师友探究
例:如图在□ABCD中,对角线AC和BD相交于点O,△ABO是等边三角形,AB=4.
求□ABCD的面积.
A
B
C
D
O
第二步:互助探究
环节2:教师讲解
4
第三步:分层提高
环节1:师友训练
先自主完成,再请师傅检查
1、能够判断一个四边形是矩形是( )
A 对角线相等; B 有一个角是直角
C 对角线垂直且相等; D 四个角都相等
2、如图,下列条件能判断
四边形ABCD是矩形的是( ).
A、AC=BD
B、OA=OC,OB=OD
C、OA=OC=OB=OD
D、AC⊥BD且OA=OC,OB=OD
A
B
C
D
O
D
C
3、已知:如图,M为□ABCD
边AD的中点,且MB=MC.
求证: □ ABCD是矩形.
A
B
C
D
M
4、已知:如图,菱形ABCD中,对角线AC和BD相 交于点O,CM∥BD,DM∥AC.
求证:四边形OCMD是矩形.
A
B
C
D
O
M
第三步:分层提高
环节1:师友训练
3、已知:如图,M为□ABCD
边AD的中点,且MB=MC.
求证:四边形ABCD是矩形.
A
B
C
D
M
4、已知:如图,菱形ABCD中,对角线AC和BD相交于点O,CM∥BD,DM∥AC.
求证:四边形OCMD是矩形.
A
B
C
D
O
M
第三步:分层提高
环节2:教师提升
要判定一个四边形是矩形,通常先判定它是平行四边形,再判定有一个角是直角或者对角线相等。
一个直角
对角线相等
四边形
平行四边形
矩形
这节课我们都学了
哪些知识?
你有哪些收获?
自己觉得哪些
地方容易出错?
学海归来
第四步:总结归纳
我想对我的师傅
(学友)说……
环节1:师友总结
1.矩形的判定方法:
解决一个数学问题,常要通过
“ 猜想”--“验证猜想(证明)”--“得出结论”
2.本节课所学的解决问题的思路:
矩形的判定口诀:
任意一个四边形,
三个直角定矩形。
对于平行四边形,
一个直角即可定;
对线相等也可定。
环节2:教师归纳
第四步:总结归纳
16
A
D
C
B
┙
┖
五、巩固反馈:
一个木匠要制作矩形的踏板,他在一个对边平行的长木板上分别沿与长边垂直的方向锯了两次,他能得到矩形踏板吗?为什么?
走进生活
环节1:师友检测
课后作业
巩固作业
<<新课程学习>>本课时
五、巩固反馈:
评一评这节课的最佳师友
环节2:教师评价
第十九章 特殊平行四边形
19.2.2、矩形的性质与判定
第一步:交流预习
环节1:教师提问
O
D
C
B
A
一、什么叫矩形?矩形有哪些性质?
二、填空
1、矩形具有而一般的平行四边形不具有的性质是( )
A.对角相等 B.对边平行且相等
C.对角线相等 D.对角线互相平分
2、下列性质中,矩形不一定具有的是( ) A.是中心对称图形 B.四个角都相等
C.是轴对称图形 D.对角线互相垂直
C
D
第一步:交流预习
1、回答14页和15页“做一做”和“想一想” 提出的问题,并猜想矩形有哪些判定方法?你会证明你的猜想吗?
2、回答15页“议一议”提出的问题,仅有绳子,你是怎样检查门框是矩形的?
3、自学15页例2,并指
出每一步的理由。
O
D
C
B
A
环节2:师友交流
请把你预习中的疑惑与师傅交流
第二步:互助探究
环节1:师友探究
矩形还有哪些判定方法?请说出你的猜想?
猜想1:对角线相等的平行四边形是矩形
猜想2:有三个角是直角的四边形是矩形.
矩形的定义:
有一个角是直角的平行四边形是矩形。
探究矩形的判定
命题:对角线相等的平行四边形是矩形。
已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。
证明:
∵ AB=CD, BC=CB, AC=BD
∴ △ABC≌ △DCB(SSS)
∵ AB//CD
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=∠DCB=90°
∴ ∠ABC=∠DCB
∴ ABCD是矩形
O
D
C
B
A
又∵ 四边形ABCD是平行四边形
已知:在四边形ABCD中,∠A=∠B=∠C=90°
求证:四边形ABCD是矩形。
A
B
C
D
∟
∟
∟
证明:∵ ∠A=∠B=90°
∴ ∠A+∠B=180°
∴AD∥BC
同理可证:AB∥CD
∴四边形ABCD是平行四边形
又∵ ∠A=90°
∴四边形ABCD是矩形
命题:有三个角是直角的四边形是矩形。
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
矩形的判定方法:
定义:
定理:
定理:
如果四边形ABCD的对角线AC=BD,这样的四边形是不是矩形
A
B
C
D
AC=BD
A
B
C
D
AC=BD
都不是矩形
想一想
18 七月 2022
情境:仅有一根绳子,你能检查窗框是否是矩形吗?你是怎样检查的?
第二步:互助探究
环节1:师友探究
例:如图在□ABCD中,对角线AC和BD相交于点O,△ABO是等边三角形,AB=4.
求□ABCD的面积.
A
B
C
D
O
第二步:互助探究
环节2:教师讲解
4
第三步:分层提高
环节1:师友训练
先自主完成,再请师傅检查
1、能够判断一个四边形是矩形是( )
A 对角线相等; B 有一个角是直角
C 对角线垂直且相等; D 四个角都相等
2、如图,下列条件能判断
四边形ABCD是矩形的是( ).
A、AC=BD
B、OA=OC,OB=OD
C、OA=OC=OB=OD
D、AC⊥BD且OA=OC,OB=OD
A
B
C
D
O
D
C
3、已知:如图,M为□ABCD
边AD的中点,且MB=MC.
求证: □ ABCD是矩形.
A
B
C
D
M
4、已知:如图,菱形ABCD中,对角线AC和BD相 交于点O,CM∥BD,DM∥AC.
求证:四边形OCMD是矩形.
A
B
C
D
O
M
第三步:分层提高
环节1:师友训练
3、已知:如图,M为□ABCD
边AD的中点,且MB=MC.
求证:四边形ABCD是矩形.
A
B
C
D
M
4、已知:如图,菱形ABCD中,对角线AC和BD相交于点O,CM∥BD,DM∥AC.
求证:四边形OCMD是矩形.
A
B
C
D
O
M
第三步:分层提高
环节2:教师提升
要判定一个四边形是矩形,通常先判定它是平行四边形,再判定有一个角是直角或者对角线相等。
一个直角
对角线相等
四边形
平行四边形
矩形
这节课我们都学了
哪些知识?
你有哪些收获?
自己觉得哪些
地方容易出错?
学海归来
第四步:总结归纳
我想对我的师傅
(学友)说……
环节1:师友总结
1.矩形的判定方法:
解决一个数学问题,常要通过
“ 猜想”--“验证猜想(证明)”--“得出结论”
2.本节课所学的解决问题的思路:
矩形的判定口诀:
任意一个四边形,
三个直角定矩形。
对于平行四边形,
一个直角即可定;
对线相等也可定。
环节2:教师归纳
第四步:总结归纳
16
A
D
C
B
┙
┖
五、巩固反馈:
一个木匠要制作矩形的踏板,他在一个对边平行的长木板上分别沿与长边垂直的方向锯了两次,他能得到矩形踏板吗?为什么?
走进生活
环节1:师友检测
课后作业
巩固作业
<<新课程学习>>本课时
五、巩固反馈:
评一评这节课的最佳师友
环节2:教师评价
