3.1 探索勾股定理同步练习(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
第三章 勾股定理
1 探索勾股定理
基础过关
知识点1 勾股定理
1.在Rt△ABC中,∠C=90°,AB=5,则 ( )
A.5 B.10 C.20 D.25
2.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,已知BC=8,AC=6,则CD=( )
A.10 B.5
3.如图,点E在正方形ABCD的边AB上,若 则正方形ABCD的面积为__________.
4.如果直角三角形的三边长分别为6,8,x,那么以x为边长的正方形的面积为__________.
5.如图,数字代表所在正方形的面积,则A所代表的正方形的面积为___________.
知识点2 勾股定理的验证
6.在勾股定理的学习过程中,我们已经学会了运用以下图形,验证著名的勾股定理.这种根据图形直观推论或验证数学规律和公式的方法,简称“无字证明”.实际上它也可用于验证数与代数,图形与几何等领域中的许多数学公式和规律,它体现的数学思想是( )
A.统计思想 B.分类思想 C.数形结合思想 D.函数思想
7.历史上对勾股定理的一种证法采用了如图所示的图形,其中两个全等的直角三角形的边AE和EB在一条直线上.证明中用到的面积相等的关系是( )
知识点3 勾股定理的应用
8.一个直角三角形的菜园,一条直角边长为5m,斜边长为13m,则这个菜园的面积为( )
A.30m B.32.5m C.26m D.60m
9.一辆拖拉机沿着笔直的公路l以20km/h的速度前行,幼儿园R距离公路3km,拖拉机产生的噪音能够影响周围5 km的区域,则幼儿园学生受拖拉机噪音影响持续的时间为( )
A.0.4 h B.0.8 h C.0.6 h D.0.7 h
10.有一块边长为40米的正方形绿地ABCD,如图所示,在BC上的E处有健身器材, 米.由于居住在A处的居民去健身踩踏了绿地,小明想在A处竖立一个标牌“少走■米,踏之何忍”.请你通过计算,帮小明在标牌的■处填上适当的数.
能力提升
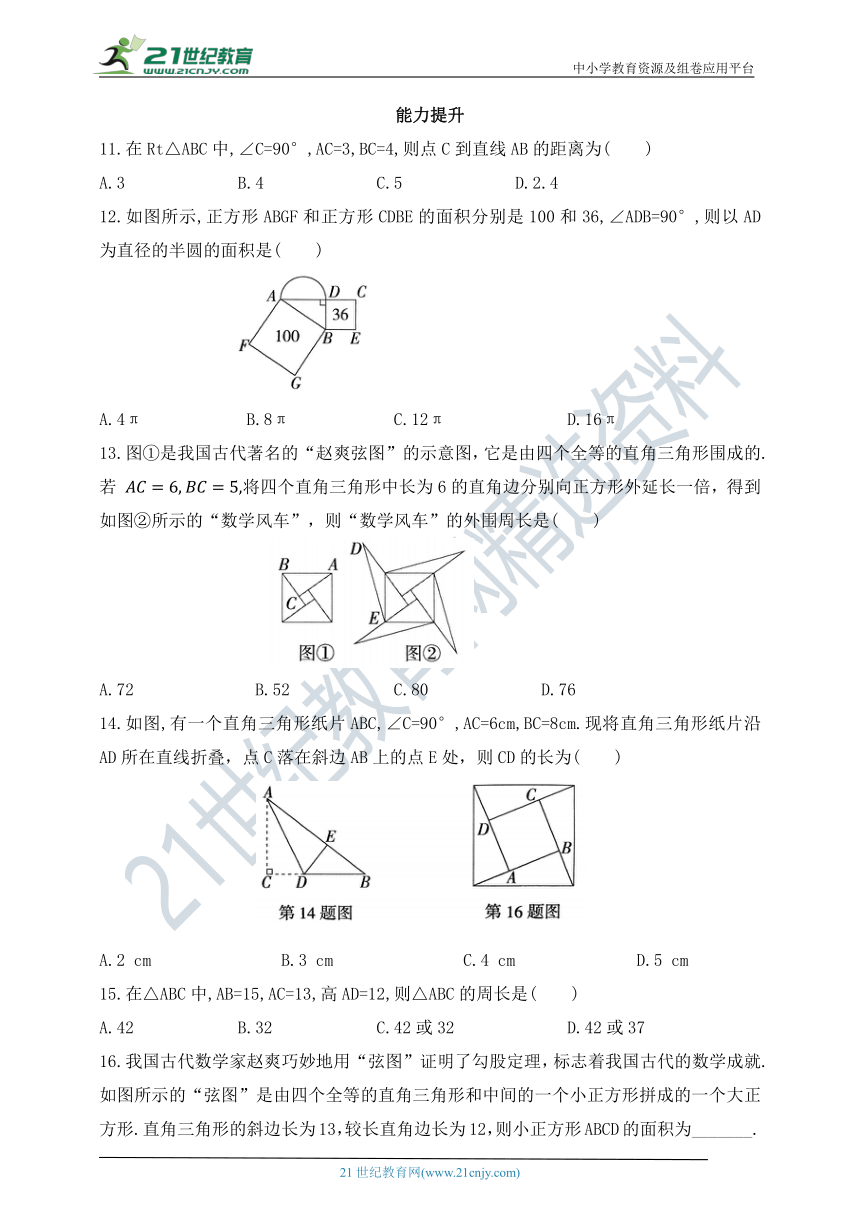
11.在Rt△ABC中,∠C=90°,AC=3,BC=4,则点C到直线AB的距离为( )
A.3 B.4 C.5 D.2.4
12.如图所示,正方形ABGF和正方形CDBE的面积分别是100和36,∠ADB=90°,则以AD为直径的半圆的面积是( )
A.4π B.8π C.12π D.16π
13.图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若 将四个直角三角形中长为6的直角边分别向正方形外延长一倍,得到如图②所示的“数学风车”,则“数学风车”的外围周长是( )
A.72 B.52 C.80 D.76
14.如图,有一个直角三角形纸片ABC,∠C=90°,AC=6cm,BC=8cm.现将直角三角形纸片沿AD所在直线折叠,点C落在斜边AB上的点E处,则CD的长为( )
A.2 cm B.3 cm C.4 cm D.5 cm
15.在△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长是( )
A.42 B.32 C.42或32 D.42或37
16.我国古代数学家赵爽巧妙地用“弦图”证明了勾股定理,标志着我国古代的数学成就.如图所示的“弦图”是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形.直角三角形的斜边长为13,较长直角边长为12,则小正方形ABCD的面积为_______.
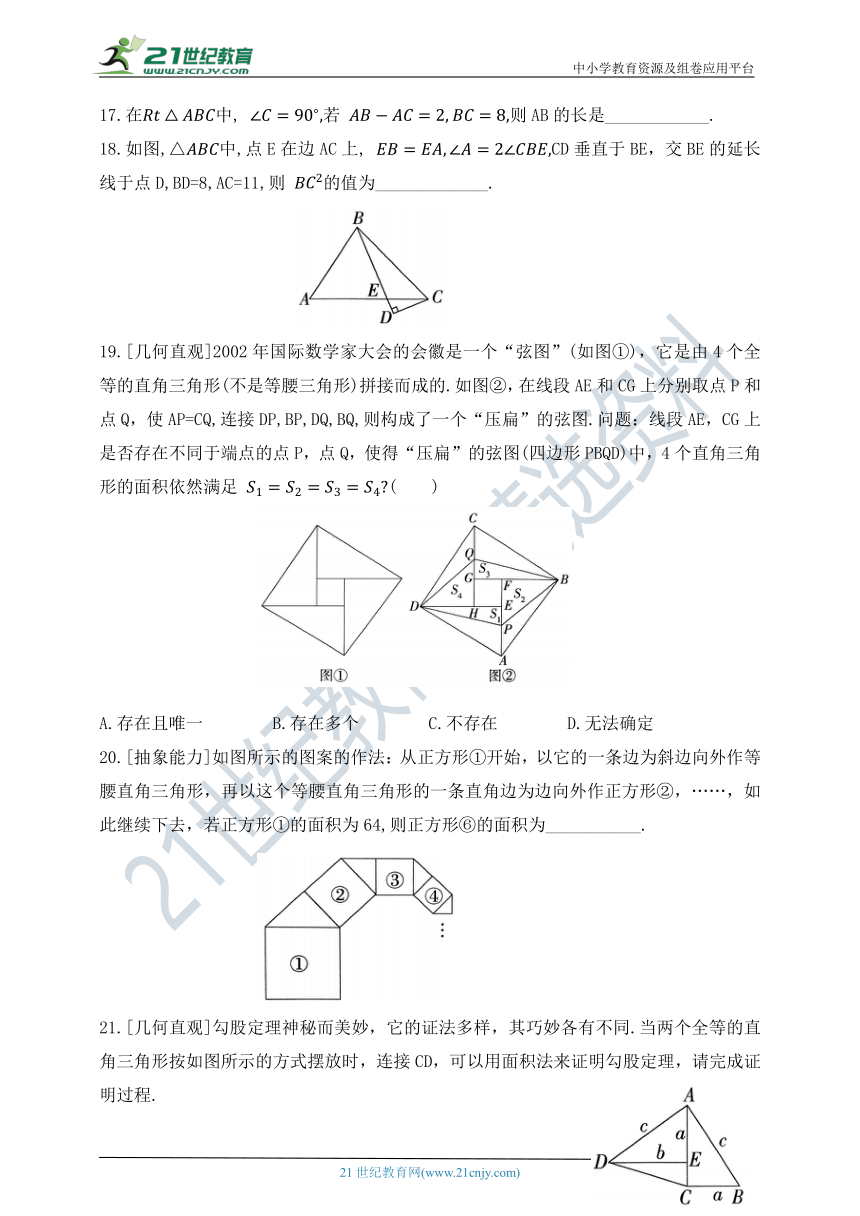
17.在中, 若 则AB的长是____________.
18.如图,△中,点E在边AC上, CD垂直于BE,交BE的延长线于点D,BD=8,AC=11,则 的值为_____________.
19.[几何直观]2002年国际数学家大会的会徽是一个“弦图”(如图①),它是由4个全等的直角三角形(不是等腰三角形)拼接而成的.如图②,在线段AE和CG上分别取点P和点Q,使AP=CQ,连接DP,BP,DQ,BQ,则构成了一个“压扁”的弦图.问题:线段AE,CG上是否存在不同于端点的点P,点Q,使得“压扁”的弦图(四边形PBQD)中,4个直角三角形的面积依然满足 ( )
A.存在且唯一 B.存在多个 C.不存在 D.无法确定
20.[抽象能力]如图所示的图案的作法:从正方形①开始,以它的一条边为斜边向外作等腰直角三角形,再以这个等腰直角三角形的一条直角边为边向外作正方形②,……,如此继续下去,若正方形①的面积为64,则正方形⑥的面积为___________.
21.[几何直观]勾股定理神秘而美妙,它的证法多样,其巧妙各有不同.当两个全等的直角三角形按如图所示的方式摆放时,连接CD,可以用面积法来证明勾股定理,请完成证明过程.
参考答案
基础过关
1.D 在 中, ∴ 故选D.
2.C 在 中,由勾股定理得 因为BC=8,AC=6,所以 因为 ·所以 故选C.
3.答案 3
解析 由勾股定理得 ∴正方形ABCD的面积
4.答案 100或28
解析 分两种情况讨论:
①当x为斜边长时,根据勾股定理,得 故以x为边长的正方形的面积为100;
②当8为斜边长时,根据勾股定理,得 28,故以x为边长的正方形的面积为28.
综上,以x为边长的正方形的面积为100或28.
5.答案 100
解析 由题意可知,直角三角形中,一条直角边长的平方=36,另一条直角边长的平方=64,则斜边长的平方 故A所代表的正方形的面积为100.
6.C 本题体现了数形结合思想,故选C.
7.D 从整体看,可按梯形的面积公式计算梯形的面积;从部分看,直角梯形的面积等于三个直角三角形的面积和,故选D.
8.A 由题意得另一条直角边长的平方= 13 -5 =144(m ),所以另一条直角边长为12m,所以这个菜园的面积为 故选A.
9.A 如图,过点R作RBLl于点B,由题意可得,RB根据勾股定理,得 所以 同理可得 所以AC所以幼儿园学生受拖拉机噪音影响持续的时间为 故选A.
10.解析 在Rt△ABE中, 41 (米 ),∴AE=41米,∵AB+BE-AE=40+9-41=8(米),∴标牌的■处填8.
能力提升
11.D 作CDLAB于点D,如图所示,因为∠ACB=90°,AC=3,BC=4,所以 25,所以AB=5,
因为 所以 2.4,所以点C到直线AB的距离为2.4,故选D.
12.B 由题可知在Rt△ABD中,∠ADB=90°,AB =100,BD =36,所以AD =100-36=64,所以AD=8,所以以AD为直径的半圆的面积是π·故选B.
13.D 依题意,设DE的长为x,则 =169,所以x=13,所以“数学风车”的外围周长是(13+6)×4=76.故选D.
14.B 在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,∴AB =AC +BC =100 cm ,∴AB=10 cm,由题意得 90°,∴EB=AB-AE=10-6=4(cm),∠DEB=90°,设DE=CD=x cm,则 在 中, ∴CD=3cm.故选B.
15.C 如图,在Rt△ABD中, 12 =81,∴BD=9,在 中,
(1)当△ABC为锐角三角形时,如图1, BD=5+9=14,∴△ABC的周长为
(2)当△ABC为钝角三角形时,如图2, 的周长为
综上所述, 的周长是42或32.故选C.
16.答案 49
解析 如图,由题意知 根据勾股定理,得 所以 所以 所以小正方形ABCD的面积为
17.答案 17
解析 在Rt△ABC中,∠C=90°,AB-AC=2,即即 解得AB=17.
18.答案 80
解析 如图,延长BD到F,使得DF=BD,连接CF, ∴CD垂直平分BF,∴ ∴∠F=∠CBD,过点C作CH∥AB,交BF于点H,则
∵EA=EB,∴∠A=∠ABD,∴∠A=∠CHD,
∵∠A=2∠CBD=2∠F,∴∠CHD=2∠F,易知∠F=∠FCH,∴HF=HC,易知AC=BH,
∵BD=8,AC=11,∴DH=BH-BD=AC-BD=3,
∵DF=BD=8,∴HC=HF=8-3=5,在Rt△CDH中,由勾股定理得
在Rt△BCD中,
19.C 因为△BCG≌△CDH≌△DAE≌△ABF,所以因为 CQ,所以 易证△则 S ,易证△
则 设 a,DE=b,则 因为a≠b,所以 故选C.
20.答案 2
解析 正方形①的面积是64,正方形②的面积是64正方形③的面积是 ……,正方形 的面积是 所以正方形⑥的面积是2.
21.证明 如图,连接DB,作 交BC的延长线于点F,
由题可知,
即 =90°,易证△
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章 勾股定理
1 探索勾股定理
基础过关
知识点1 勾股定理
1.在Rt△ABC中,∠C=90°,AB=5,则 ( )
A.5 B.10 C.20 D.25
2.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,已知BC=8,AC=6,则CD=( )
A.10 B.5
3.如图,点E在正方形ABCD的边AB上,若 则正方形ABCD的面积为__________.
4.如果直角三角形的三边长分别为6,8,x,那么以x为边长的正方形的面积为__________.
5.如图,数字代表所在正方形的面积,则A所代表的正方形的面积为___________.
知识点2 勾股定理的验证
6.在勾股定理的学习过程中,我们已经学会了运用以下图形,验证著名的勾股定理.这种根据图形直观推论或验证数学规律和公式的方法,简称“无字证明”.实际上它也可用于验证数与代数,图形与几何等领域中的许多数学公式和规律,它体现的数学思想是( )
A.统计思想 B.分类思想 C.数形结合思想 D.函数思想
7.历史上对勾股定理的一种证法采用了如图所示的图形,其中两个全等的直角三角形的边AE和EB在一条直线上.证明中用到的面积相等的关系是( )
知识点3 勾股定理的应用
8.一个直角三角形的菜园,一条直角边长为5m,斜边长为13m,则这个菜园的面积为( )
A.30m B.32.5m C.26m D.60m
9.一辆拖拉机沿着笔直的公路l以20km/h的速度前行,幼儿园R距离公路3km,拖拉机产生的噪音能够影响周围5 km的区域,则幼儿园学生受拖拉机噪音影响持续的时间为( )
A.0.4 h B.0.8 h C.0.6 h D.0.7 h
10.有一块边长为40米的正方形绿地ABCD,如图所示,在BC上的E处有健身器材, 米.由于居住在A处的居民去健身踩踏了绿地,小明想在A处竖立一个标牌“少走■米,踏之何忍”.请你通过计算,帮小明在标牌的■处填上适当的数.
能力提升
11.在Rt△ABC中,∠C=90°,AC=3,BC=4,则点C到直线AB的距离为( )
A.3 B.4 C.5 D.2.4
12.如图所示,正方形ABGF和正方形CDBE的面积分别是100和36,∠ADB=90°,则以AD为直径的半圆的面积是( )
A.4π B.8π C.12π D.16π
13.图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若 将四个直角三角形中长为6的直角边分别向正方形外延长一倍,得到如图②所示的“数学风车”,则“数学风车”的外围周长是( )
A.72 B.52 C.80 D.76
14.如图,有一个直角三角形纸片ABC,∠C=90°,AC=6cm,BC=8cm.现将直角三角形纸片沿AD所在直线折叠,点C落在斜边AB上的点E处,则CD的长为( )
A.2 cm B.3 cm C.4 cm D.5 cm
15.在△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长是( )
A.42 B.32 C.42或32 D.42或37
16.我国古代数学家赵爽巧妙地用“弦图”证明了勾股定理,标志着我国古代的数学成就.如图所示的“弦图”是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形.直角三角形的斜边长为13,较长直角边长为12,则小正方形ABCD的面积为_______.
17.在中, 若 则AB的长是____________.
18.如图,△中,点E在边AC上, CD垂直于BE,交BE的延长线于点D,BD=8,AC=11,则 的值为_____________.
19.[几何直观]2002年国际数学家大会的会徽是一个“弦图”(如图①),它是由4个全等的直角三角形(不是等腰三角形)拼接而成的.如图②,在线段AE和CG上分别取点P和点Q,使AP=CQ,连接DP,BP,DQ,BQ,则构成了一个“压扁”的弦图.问题:线段AE,CG上是否存在不同于端点的点P,点Q,使得“压扁”的弦图(四边形PBQD)中,4个直角三角形的面积依然满足 ( )
A.存在且唯一 B.存在多个 C.不存在 D.无法确定
20.[抽象能力]如图所示的图案的作法:从正方形①开始,以它的一条边为斜边向外作等腰直角三角形,再以这个等腰直角三角形的一条直角边为边向外作正方形②,……,如此继续下去,若正方形①的面积为64,则正方形⑥的面积为___________.
21.[几何直观]勾股定理神秘而美妙,它的证法多样,其巧妙各有不同.当两个全等的直角三角形按如图所示的方式摆放时,连接CD,可以用面积法来证明勾股定理,请完成证明过程.
参考答案
基础过关
1.D 在 中, ∴ 故选D.
2.C 在 中,由勾股定理得 因为BC=8,AC=6,所以 因为 ·所以 故选C.
3.答案 3
解析 由勾股定理得 ∴正方形ABCD的面积
4.答案 100或28
解析 分两种情况讨论:
①当x为斜边长时,根据勾股定理,得 故以x为边长的正方形的面积为100;
②当8为斜边长时,根据勾股定理,得 28,故以x为边长的正方形的面积为28.
综上,以x为边长的正方形的面积为100或28.
5.答案 100
解析 由题意可知,直角三角形中,一条直角边长的平方=36,另一条直角边长的平方=64,则斜边长的平方 故A所代表的正方形的面积为100.
6.C 本题体现了数形结合思想,故选C.
7.D 从整体看,可按梯形的面积公式计算梯形的面积;从部分看,直角梯形的面积等于三个直角三角形的面积和,故选D.
8.A 由题意得另一条直角边长的平方= 13 -5 =144(m ),所以另一条直角边长为12m,所以这个菜园的面积为 故选A.
9.A 如图,过点R作RBLl于点B,由题意可得,RB根据勾股定理,得 所以 同理可得 所以AC所以幼儿园学生受拖拉机噪音影响持续的时间为 故选A.
10.解析 在Rt△ABE中, 41 (米 ),∴AE=41米,∵AB+BE-AE=40+9-41=8(米),∴标牌的■处填8.
能力提升
11.D 作CDLAB于点D,如图所示,因为∠ACB=90°,AC=3,BC=4,所以 25,所以AB=5,
因为 所以 2.4,所以点C到直线AB的距离为2.4,故选D.
12.B 由题可知在Rt△ABD中,∠ADB=90°,AB =100,BD =36,所以AD =100-36=64,所以AD=8,所以以AD为直径的半圆的面积是π·故选B.
13.D 依题意,设DE的长为x,则 =169,所以x=13,所以“数学风车”的外围周长是(13+6)×4=76.故选D.
14.B 在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,∴AB =AC +BC =100 cm ,∴AB=10 cm,由题意得 90°,∴EB=AB-AE=10-6=4(cm),∠DEB=90°,设DE=CD=x cm,则 在 中, ∴CD=3cm.故选B.
15.C 如图,在Rt△ABD中, 12 =81,∴BD=9,在 中,
(1)当△ABC为锐角三角形时,如图1, BD=5+9=14,∴△ABC的周长为
(2)当△ABC为钝角三角形时,如图2, 的周长为
综上所述, 的周长是42或32.故选C.
16.答案 49
解析 如图,由题意知 根据勾股定理,得 所以 所以 所以小正方形ABCD的面积为
17.答案 17
解析 在Rt△ABC中,∠C=90°,AB-AC=2,即即 解得AB=17.
18.答案 80
解析 如图,延长BD到F,使得DF=BD,连接CF, ∴CD垂直平分BF,∴ ∴∠F=∠CBD,过点C作CH∥AB,交BF于点H,则
∵EA=EB,∴∠A=∠ABD,∴∠A=∠CHD,
∵∠A=2∠CBD=2∠F,∴∠CHD=2∠F,易知∠F=∠FCH,∴HF=HC,易知AC=BH,
∵BD=8,AC=11,∴DH=BH-BD=AC-BD=3,
∵DF=BD=8,∴HC=HF=8-3=5,在Rt△CDH中,由勾股定理得
在Rt△BCD中,
19.C 因为△BCG≌△CDH≌△DAE≌△ABF,所以因为 CQ,所以 易证△则 S ,易证△
则 设 a,DE=b,则 因为a≠b,所以 故选C.
20.答案 2
解析 正方形①的面积是64,正方形②的面积是64正方形③的面积是 ……,正方形 的面积是 所以正方形⑥的面积是2.
21.证明 如图,连接DB,作 交BC的延长线于点F,
由题可知,
即 =90°,易证△
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
