沪科版七年级上册1.5 有理数的乘除(第2课时)课件(共16张PPT)
文档属性
| 名称 | 沪科版七年级上册1.5 有理数的乘除(第2课时)课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-19 09:05:15 | ||
图片预览






文档简介
(共16张PPT)
第1章 有理数
1.5 有理数的乘除
第2课时 有理数乘法运算律
学 习 目 标
2
1
3
理解有理数乘法运算律;
会运用有理数乘法运算律简化计算.(难点)
理解多个有理数乘法的法则,会进行多个有理数乘法运算;(重点)
温故知新
有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数与0相乘,都得0.
一个数与1相乘,仍得原数.
一个数与-1相乘,得原数的相反数.
观察下列各式,它们的积是正的还是负的?
1、2×3×4×(-5)______
2、2×3×(-4)×(-5)________
3、2×(-3)×(-4)×(-5)______
4、(-2)×(-3)×(-4)×(-5)__
5、7.8×(8.1)×0×(-19.6)______
负
正
负
正
几个不是0的数相乘,积的符号与负因数的个数之间有什么关系?
有一因数为 0 时,积是多少?
0
探究(1)
知识讲解
几个不是0的数相乘,积的符号由_____决定,
负因数的个数是______时,积是负数;
负因数的个数是______时,积是正数.
奇数
偶数
负因数的个数
}
奇负偶正
几个数相乘,如果其中有因数为0,积等于____
0
归纳:
几个有理数相乘法则:
知识讲解
例1 计算:
知识讲解
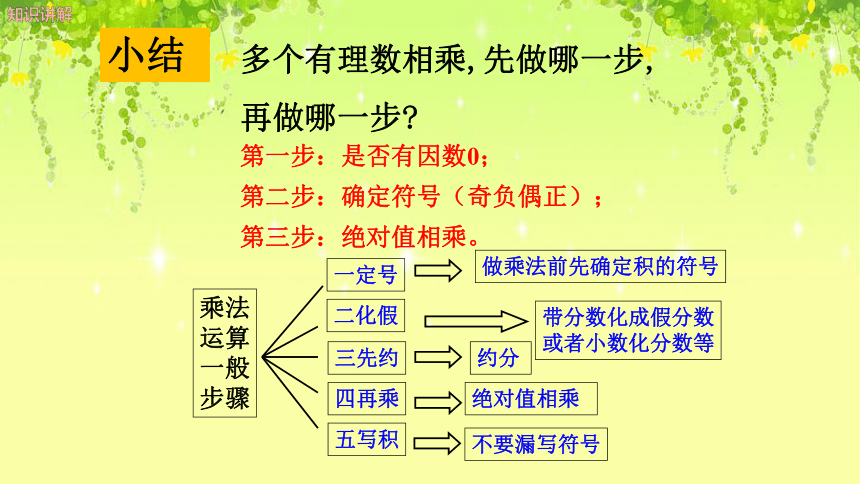
多个有理数相乘,先做哪一步,
再做哪一步
第一步:是否有因数0;
第二步:确定符号(奇负偶正);
第三步:绝对值相乘。
乘法运算
一般步骤
不要漏写符号
一定号
做乘法前先确定积的符号
二化假
带分数化成假分数
或者小数化分数等
三先约
约分
四再乘
五写积
绝对值相乘
小结
知识讲解
从这两个例子中你能总结出什么?
探究(2)
-30
-30
知识讲解
(ab)c=a(bc)
有理数乘法的运算律:
1、乘法交换律:
a×b=b×a
2、乘法结合律:
(a×b)×c=a×(b×c).
ab=ba
知识讲解
(2)(-6)×(+3.7)×( )×( ).
(-12.5)×(-2.5)×(-8)×4.
= [(-12.5)×(-8)]×[(-2.5)×4]
=100×(-10)
=-1000.
解: 原式
原式=[(-6)×( )]× ×( )
= 2 ×( ) =
例2 计算:
知识讲解
探究(3)
从这个例子中大家能得到什么结论?
知识讲解
a(b+c)=ab+ac
有理数乘法的运算律:
3、乘法分配律:
a×(b+c)=a×b+a×c.
知识讲解
(2) 4.98×(-5).
(1)60×
解: 原式
原式
例3 计算
知识讲解
(2)
(3)
(4)
1.
答案:1、 2、11 3、0 4、-250
随堂训练
随堂训练
2.
(-2.5)×2.5×(-8)×4
解:原式=-2.5 ×(-8)×2.5×4
=20 ×10
=20 0
(2)(-6)× +8 × -11×
解:原式=(-6+8-11)×
=-3
课堂小结
几个不是0的数相乘,积的符号由_____决定,
负因数的个数是______时,积是负数;
负因数的个数是______时,积是正数.
奇数
偶数
负因数的个数
}
奇负偶正
几个数相乘,如果其中有因数为0,积等于____
0
1、几个有理数相乘法则:
2、有理数乘法运算律:
(1)乘法的交换律: ab=ba
(2)乘法的结合律: (ab)c = a(bc )
(3)乘法的分配律: a(b+c)=ab+ac
第1章 有理数
1.5 有理数的乘除
第2课时 有理数乘法运算律
学 习 目 标
2
1
3
理解有理数乘法运算律;
会运用有理数乘法运算律简化计算.(难点)
理解多个有理数乘法的法则,会进行多个有理数乘法运算;(重点)
温故知新
有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数与0相乘,都得0.
一个数与1相乘,仍得原数.
一个数与-1相乘,得原数的相反数.
观察下列各式,它们的积是正的还是负的?
1、2×3×4×(-5)______
2、2×3×(-4)×(-5)________
3、2×(-3)×(-4)×(-5)______
4、(-2)×(-3)×(-4)×(-5)__
5、7.8×(8.1)×0×(-19.6)______
负
正
负
正
几个不是0的数相乘,积的符号与负因数的个数之间有什么关系?
有一因数为 0 时,积是多少?
0
探究(1)
知识讲解
几个不是0的数相乘,积的符号由_____决定,
负因数的个数是______时,积是负数;
负因数的个数是______时,积是正数.
奇数
偶数
负因数的个数
}
奇负偶正
几个数相乘,如果其中有因数为0,积等于____
0
归纳:
几个有理数相乘法则:
知识讲解
例1 计算:
知识讲解
多个有理数相乘,先做哪一步,
再做哪一步
第一步:是否有因数0;
第二步:确定符号(奇负偶正);
第三步:绝对值相乘。
乘法运算
一般步骤
不要漏写符号
一定号
做乘法前先确定积的符号
二化假
带分数化成假分数
或者小数化分数等
三先约
约分
四再乘
五写积
绝对值相乘
小结
知识讲解
从这两个例子中你能总结出什么?
探究(2)
-30
-30
知识讲解
(ab)c=a(bc)
有理数乘法的运算律:
1、乘法交换律:
a×b=b×a
2、乘法结合律:
(a×b)×c=a×(b×c).
ab=ba
知识讲解
(2)(-6)×(+3.7)×( )×( ).
(-12.5)×(-2.5)×(-8)×4.
= [(-12.5)×(-8)]×[(-2.5)×4]
=100×(-10)
=-1000.
解: 原式
原式=[(-6)×( )]× ×( )
= 2 ×( ) =
例2 计算:
知识讲解
探究(3)
从这个例子中大家能得到什么结论?
知识讲解
a(b+c)=ab+ac
有理数乘法的运算律:
3、乘法分配律:
a×(b+c)=a×b+a×c.
知识讲解
(2) 4.98×(-5).
(1)60×
解: 原式
原式
例3 计算
知识讲解
(2)
(3)
(4)
1.
答案:1、 2、11 3、0 4、-250
随堂训练
随堂训练
2.
(-2.5)×2.5×(-8)×4
解:原式=-2.5 ×(-8)×2.5×4
=20 ×10
=20 0
(2)(-6)× +8 × -11×
解:原式=(-6+8-11)×
=-3
课堂小结
几个不是0的数相乘,积的符号由_____决定,
负因数的个数是______时,积是负数;
负因数的个数是______时,积是正数.
奇数
偶数
负因数的个数
}
奇负偶正
几个数相乘,如果其中有因数为0,积等于____
0
1、几个有理数相乘法则:
2、有理数乘法运算律:
(1)乘法的交换律: ab=ba
(2)乘法的结合律: (ab)c = a(bc )
(3)乘法的分配律: a(b+c)=ab+ac
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
