3.3 勾股定理的应用举例同步练习(含答案)
文档属性
| 名称 | 3.3 勾股定理的应用举例同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 9.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 10:35:46 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第三章 勾股定理
3 勾股定理的应用举例
基础过关
知识点1 确定几何体上的最短路线
1.将一根24cm长的筷子置于底面直径为15cm,高为8cm的装满水的无盖圆柱形水杯中,设筷子浸没在水里的长度为h cm,则h的取值范围是( )
2.如图是一个底面为等边三角形的三棱柱,小丽在三棱柱的侧面,从顶点A到顶点镶上一圈金属丝,已知此三棱柱的高为5 cm,底面边长为4 cm,则这圈金属丝的长度至少为( )
3.如图是滑板爱好者使用的U型池,该U型池可以看成是一个长方体去掉一个“半圆柱”而成的,中间可供滑行的部分的截面是半径为2.5m的半圆,其边缘.小明要在AB上选取一点E,使他从点D滑到点E再滑到点C的滑行路程最短,则他滑行的最短路程约为(π取3).
知识点2 利用直角三角形的判别条件判定垂直
4.李老师想用三根木条做一个直角三角形作为教具,用以下四组长度的木条,刚好能够做成直角三角形的是( )
5.如图,某港口P位于东西方向的海岸线上,甲、乙两艘轮船同时离开港口,各自沿固定方向航行,甲、乙两艘轮船每小时分别航行12海里和16海里,1小时后两船分别位于点A,B处,且相距20海里,如果甲船沿北偏西40°方向航行,则乙船沿_________方向航行.
知识点3 利用勾股定理解决实际问题
6.《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何 ”其大意:今有一门,高比宽多6尺8寸,门的对角线长恰好为1丈.问门的高、宽各是多少 (1丈=10尺,1尺=10寸)如图,设门的高AB为x尺,根据题意,可列方程为________________.
7.如图是一个滑梯示意图,左边是楼梯,右边是滑道,已知滑道AC与AE的长度一样,滑梯的高度则滑道AC的长为.
8.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,则船向岸边移动了_________米.
9.如图是两个冰壶运动兴趣小队比赛时,两个冰壶所在位置的平面示意图,数据如图所示(单位:cm),则两个冰壶中心点A、B之间的距离为___________.
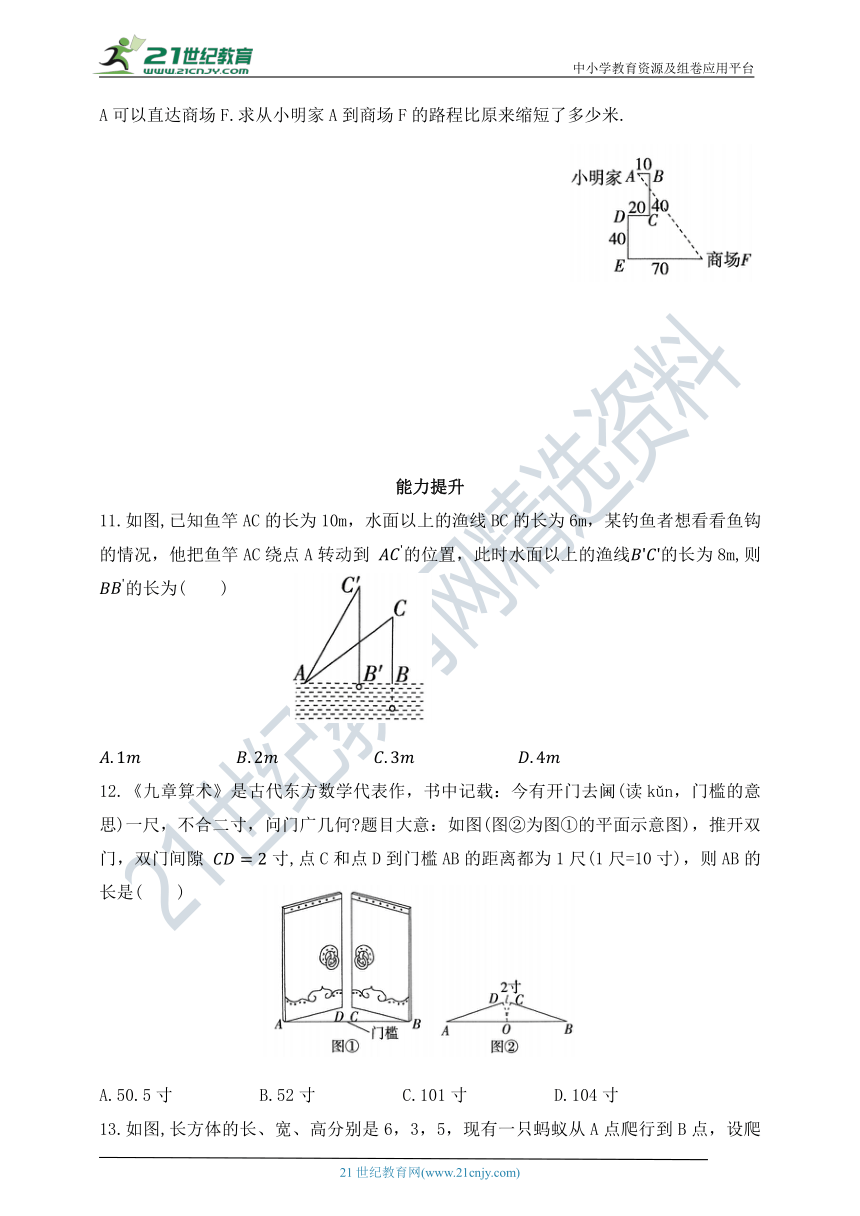
10.某市进行老城区道路改造,原来从小明家A到商场F需要沿着A→B→C→D→E→F连续多次直角拐弯行进,出行十分麻烦(数据如图所示,单位:米),道路改造后从小明家A可以直达商场F.求从小明家A到商场F的路程比原来缩短了多少米.
能力提升
11.如图,已知鱼竿AC的长为10m,水面以上的渔线BC的长为6m,某钓鱼者想看看鱼钩的情况,他把鱼竿AC绕点A转动到 的位置,此时水面以上的渔线的长为8m,则 的长为( )
12.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何 题目大意:如图(图②为图①的平面示意图),推开双门,双门间隙 寸,点C和点D到门槛AB的距离都为1尺(1尺=10寸),则AB的长是( )
A.50.5寸 B.52寸 C.101寸 D.104寸
13.如图,长方体的长、宽、高分别是6,3,5,现有一只蚂蚁从A点爬行到B点,设爬行的最短路线长为a,则a 的值是( )
A.130 B.106 C.100 D.86
14.《九章算术》中一道“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何 ”题意:如图,有一个池塘,其底面是边长为10尺的正方形,一棵芦苇AC生长在它的中央,高出水面部分BC的长为1尺,如果把
该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部C恰好到岸边的C'处,水深和芦苇长各多少尺 则该问题的水深是____________尺.
15.无盖圆柱形杯子的展开图如图所示.将一根长为20cm的筷子斜放在该杯子内,筷子露在杯子外面的部分至少有___________cm.
16.[模型观念]如图,牧童在A处放牛,牧童家在B处,A、B处距河岸DC的距离AC、BD的长分别为5km、10km,且C,D两点之间的距离为8km,天黑前牧童从A处将牛牵到河边饮水再回家,那么牧童最少要走( )
17.[模型观念]如图,台风中心从点B沿射线BC的方向以 的速度向点D移动,已知A、B两点之间的距离为130km,点A到BC的距离 那么台风中心经过多长时间从点B移到点D 如果在距台风中心30km的圆形区域内都有遭遇台风的危险,正在D点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险 (台风中心在点B时,游人接到台风警报,假设游人从D点撤离就可以脱离危险)
参考答案
基础过关
1.C 当筷子竖立在水杯中时,筷子浸没在水里的长度最短,为8cm;如图,AD是筷子,AB是水杯的底面直径,BC是水杯的高,当筷子按如图所示的方式斜放于水杯中时,浸没在水里的部分最长.由题意得 是直角三角形.在 中,根据勾股定理,得 综上,8≤h≤17.故选C.
2.B 将三棱柱的侧面沿展开,如图所示, 的长度就是金属丝长度的最小值,
由勾股定理得 所以 故选B.
3.答案 25
解析 将U型池中间可供滑行的部分展平,如图,作点C关于直线AB的对称点F,连接DF,交AB于点E,此时 的值最小,
的截面是半径为2.5m的半圆,所以 所以 在Rt△CDF中, 所以DF=25m,所以 ,故他滑行的最短距离约为25m.
4.B 不能构成直角三角形; 能构成直角三角形; 6 ,不能构成直角三角形;D.1+2=3,不能构成三角形.故选B.
5.答案 北偏东50°
解析 由题意可知, 海里, 海里,AB=20海里,因为 所以 所以△APB是直角三角形, 由题意知∠APN=40°,所以∠BPN=90°-∠APN=50°,故乙船沿北偏东50°方向航行.
6.答案
解析 由题可知,门的高AB为x尺,门的宽为 6.8)尺,AC=1丈=10尺, 所以 即
7.答案 8.5
解析 设 则 所以在Rt△ABC中, 即 解得 所以
8.答案 9
解析 在Rt△ABC中, 米,AC=8米,
(米 ),∴AB=15米,
在 中, 米, 米,
(米 ), 米,∴BD=AB-AD=15-6=9(米),
故船向岸边移动了9米.
9.答案 150 cm
解析 如图,作 过点B作BC⊥AC于点C,易知 120 cm,在Rt△ABC中, 22500(cm ) ,
所以 所以两个冰壶中心点A、B之间的距离为150cm.
10.解析 如图所示,过点A作 于H,在Rt△AHF中, (米),FH=70-20+10=60(米),由勾股定理得AF=100米,故改造后从小明家A到商场F的路程为100米,改造前从小明家A到商场F的路程为 180(米), (米).
答:从小明家A到商场F的路程比原来缩短了80米.
能力提升
11.B 在 中,AC=10m,BC=6m,所以AB 所以 ,在中, 所以 所以 所以 故选B.
12.C 过D作DE⊥AB于E,如图所示.
由题意得 尺=10寸,OE寸,设 寸,则AB=2r寸, 寸,在 中, 即 解得r=50.5,∴2r=101, 寸,故选C.
13.C (1)把题图中长方体的正面和上面展开,如图①,则
(2)把题图中长方体的左面和上面展开,如图②,则
(3)把题图中长方体的正面和右面展开,如图③,则
因为,所以a =100.故选C.
14.答案 12
解析 设芦苇长为x尺,即 尺,则AB=(x-1)尺,由题可知 (尺),在中, 即 解得x=13,所以x-1=12,故水深为12尺,
15.答案 5
解析 由勾股定理可得杯子内筷子的最大长度为15cm,则筷子露在杯子外面的部分至少有20-15=5(cm).
16.C 如图,作A点关于河岸DC的对称点,连接交CD于点P,连接PA,过作⊥BD,交BD的延长线于,此时PA+PB的值最小,即牧童要走的路程最短,易知所以 在中, 所以 故牧童最少要走17 km.故选C.
17.解析 在 中,根据勾股定理,得 ∴BD =120km,120÷15=8(h),则台风中心经过8h从点B移动到点D.
如图,∵距台风中心30km的圆形区域内都有遭遇台风的危险,∴游人要在台风中心到达点E之前撤离,BE=BD-DE=120-30=90(km),90÷15=6(h),∴游人在6h内撤离才可脱离危险.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章 勾股定理
3 勾股定理的应用举例
基础过关
知识点1 确定几何体上的最短路线
1.将一根24cm长的筷子置于底面直径为15cm,高为8cm的装满水的无盖圆柱形水杯中,设筷子浸没在水里的长度为h cm,则h的取值范围是( )
2.如图是一个底面为等边三角形的三棱柱,小丽在三棱柱的侧面,从顶点A到顶点镶上一圈金属丝,已知此三棱柱的高为5 cm,底面边长为4 cm,则这圈金属丝的长度至少为( )
3.如图是滑板爱好者使用的U型池,该U型池可以看成是一个长方体去掉一个“半圆柱”而成的,中间可供滑行的部分的截面是半径为2.5m的半圆,其边缘.小明要在AB上选取一点E,使他从点D滑到点E再滑到点C的滑行路程最短,则他滑行的最短路程约为(π取3).
知识点2 利用直角三角形的判别条件判定垂直
4.李老师想用三根木条做一个直角三角形作为教具,用以下四组长度的木条,刚好能够做成直角三角形的是( )
5.如图,某港口P位于东西方向的海岸线上,甲、乙两艘轮船同时离开港口,各自沿固定方向航行,甲、乙两艘轮船每小时分别航行12海里和16海里,1小时后两船分别位于点A,B处,且相距20海里,如果甲船沿北偏西40°方向航行,则乙船沿_________方向航行.
知识点3 利用勾股定理解决实际问题
6.《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何 ”其大意:今有一门,高比宽多6尺8寸,门的对角线长恰好为1丈.问门的高、宽各是多少 (1丈=10尺,1尺=10寸)如图,设门的高AB为x尺,根据题意,可列方程为________________.
7.如图是一个滑梯示意图,左边是楼梯,右边是滑道,已知滑道AC与AE的长度一样,滑梯的高度则滑道AC的长为.
8.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,则船向岸边移动了_________米.
9.如图是两个冰壶运动兴趣小队比赛时,两个冰壶所在位置的平面示意图,数据如图所示(单位:cm),则两个冰壶中心点A、B之间的距离为___________.
10.某市进行老城区道路改造,原来从小明家A到商场F需要沿着A→B→C→D→E→F连续多次直角拐弯行进,出行十分麻烦(数据如图所示,单位:米),道路改造后从小明家A可以直达商场F.求从小明家A到商场F的路程比原来缩短了多少米.
能力提升
11.如图,已知鱼竿AC的长为10m,水面以上的渔线BC的长为6m,某钓鱼者想看看鱼钩的情况,他把鱼竿AC绕点A转动到 的位置,此时水面以上的渔线的长为8m,则 的长为( )
12.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何 题目大意:如图(图②为图①的平面示意图),推开双门,双门间隙 寸,点C和点D到门槛AB的距离都为1尺(1尺=10寸),则AB的长是( )
A.50.5寸 B.52寸 C.101寸 D.104寸
13.如图,长方体的长、宽、高分别是6,3,5,现有一只蚂蚁从A点爬行到B点,设爬行的最短路线长为a,则a 的值是( )
A.130 B.106 C.100 D.86
14.《九章算术》中一道“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何 ”题意:如图,有一个池塘,其底面是边长为10尺的正方形,一棵芦苇AC生长在它的中央,高出水面部分BC的长为1尺,如果把
该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部C恰好到岸边的C'处,水深和芦苇长各多少尺 则该问题的水深是____________尺.
15.无盖圆柱形杯子的展开图如图所示.将一根长为20cm的筷子斜放在该杯子内,筷子露在杯子外面的部分至少有___________cm.
16.[模型观念]如图,牧童在A处放牛,牧童家在B处,A、B处距河岸DC的距离AC、BD的长分别为5km、10km,且C,D两点之间的距离为8km,天黑前牧童从A处将牛牵到河边饮水再回家,那么牧童最少要走( )
17.[模型观念]如图,台风中心从点B沿射线BC的方向以 的速度向点D移动,已知A、B两点之间的距离为130km,点A到BC的距离 那么台风中心经过多长时间从点B移到点D 如果在距台风中心30km的圆形区域内都有遭遇台风的危险,正在D点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险 (台风中心在点B时,游人接到台风警报,假设游人从D点撤离就可以脱离危险)
参考答案
基础过关
1.C 当筷子竖立在水杯中时,筷子浸没在水里的长度最短,为8cm;如图,AD是筷子,AB是水杯的底面直径,BC是水杯的高,当筷子按如图所示的方式斜放于水杯中时,浸没在水里的部分最长.由题意得 是直角三角形.在 中,根据勾股定理,得 综上,8≤h≤17.故选C.
2.B 将三棱柱的侧面沿展开,如图所示, 的长度就是金属丝长度的最小值,
由勾股定理得 所以 故选B.
3.答案 25
解析 将U型池中间可供滑行的部分展平,如图,作点C关于直线AB的对称点F,连接DF,交AB于点E,此时 的值最小,
的截面是半径为2.5m的半圆,所以 所以 在Rt△CDF中, 所以DF=25m,所以 ,故他滑行的最短距离约为25m.
4.B 不能构成直角三角形; 能构成直角三角形; 6 ,不能构成直角三角形;D.1+2=3,不能构成三角形.故选B.
5.答案 北偏东50°
解析 由题意可知, 海里, 海里,AB=20海里,因为 所以 所以△APB是直角三角形, 由题意知∠APN=40°,所以∠BPN=90°-∠APN=50°,故乙船沿北偏东50°方向航行.
6.答案
解析 由题可知,门的高AB为x尺,门的宽为 6.8)尺,AC=1丈=10尺, 所以 即
7.答案 8.5
解析 设 则 所以在Rt△ABC中, 即 解得 所以
8.答案 9
解析 在Rt△ABC中, 米,AC=8米,
(米 ),∴AB=15米,
在 中, 米, 米,
(米 ), 米,∴BD=AB-AD=15-6=9(米),
故船向岸边移动了9米.
9.答案 150 cm
解析 如图,作 过点B作BC⊥AC于点C,易知 120 cm,在Rt△ABC中, 22500(cm ) ,
所以 所以两个冰壶中心点A、B之间的距离为150cm.
10.解析 如图所示,过点A作 于H,在Rt△AHF中, (米),FH=70-20+10=60(米),由勾股定理得AF=100米,故改造后从小明家A到商场F的路程为100米,改造前从小明家A到商场F的路程为 180(米), (米).
答:从小明家A到商场F的路程比原来缩短了80米.
能力提升
11.B 在 中,AC=10m,BC=6m,所以AB 所以 ,在中, 所以 所以 所以 故选B.
12.C 过D作DE⊥AB于E,如图所示.
由题意得 尺=10寸,OE寸,设 寸,则AB=2r寸, 寸,在 中, 即 解得r=50.5,∴2r=101, 寸,故选C.
13.C (1)把题图中长方体的正面和上面展开,如图①,则
(2)把题图中长方体的左面和上面展开,如图②,则
(3)把题图中长方体的正面和右面展开,如图③,则
因为,所以a =100.故选C.
14.答案 12
解析 设芦苇长为x尺,即 尺,则AB=(x-1)尺,由题可知 (尺),在中, 即 解得x=13,所以x-1=12,故水深为12尺,
15.答案 5
解析 由勾股定理可得杯子内筷子的最大长度为15cm,则筷子露在杯子外面的部分至少有20-15=5(cm).
16.C 如图,作A点关于河岸DC的对称点,连接交CD于点P,连接PA,过作⊥BD,交BD的延长线于,此时PA+PB的值最小,即牧童要走的路程最短,易知所以 在中, 所以 故牧童最少要走17 km.故选C.
17.解析 在 中,根据勾股定理,得 ∴BD =120km,120÷15=8(h),则台风中心经过8h从点B移动到点D.
如图,∵距台风中心30km的圆形区域内都有遭遇台风的危险,∴游人要在台风中心到达点E之前撤离,BE=BD-DE=120-30=90(km),90÷15=6(h),∴游人在6h内撤离才可脱离危险.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
