第三章 勾股定理专项训练 勾股定理及直角三角形的判别条件同步练习(含答案)
文档属性
| 名称 | 第三章 勾股定理专项训练 勾股定理及直角三角形的判别条件同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-27 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专项训练
勾股定理及直角三角形的判别条件
类型一 判断三角形的形状
1.已知a,b,c是△ABC的三边长,且满足 ,则△ABC的形状为_____________.
类型二 说明线段垂直
2.甲、乙两艘客轮同时离开港口O,航行速度都是40米/分钟,甲客轮用30分钟到达A处,乙客轮用40分钟到达B处.若A、B之间的距离为2000米,甲客轮沿着北偏东30°方向航行,则乙客轮的航行方向可能是( )
A.北偏西30° B.南偏西30° C.南偏东60° D.南偏西60°
类型三 求线段的长
3.如图,在Rt△ABC中,∠ACB=90°,AE为△ABC的角平分线,ED⊥AB,若AC=6,BC=8,则BD的长为( )
A.2 B.3 C.4 D.5
4.如图是一个三级台阶,它的每一级的长、宽、高分别为20dm,3dm,2dm,A和B是这个台阶两个相对的端点,A点处有一只蚂蚁,想到B点吃可口的食物,求蚂蚁沿着台阶面爬到B点的最短路程.
类型四 求图形的面积
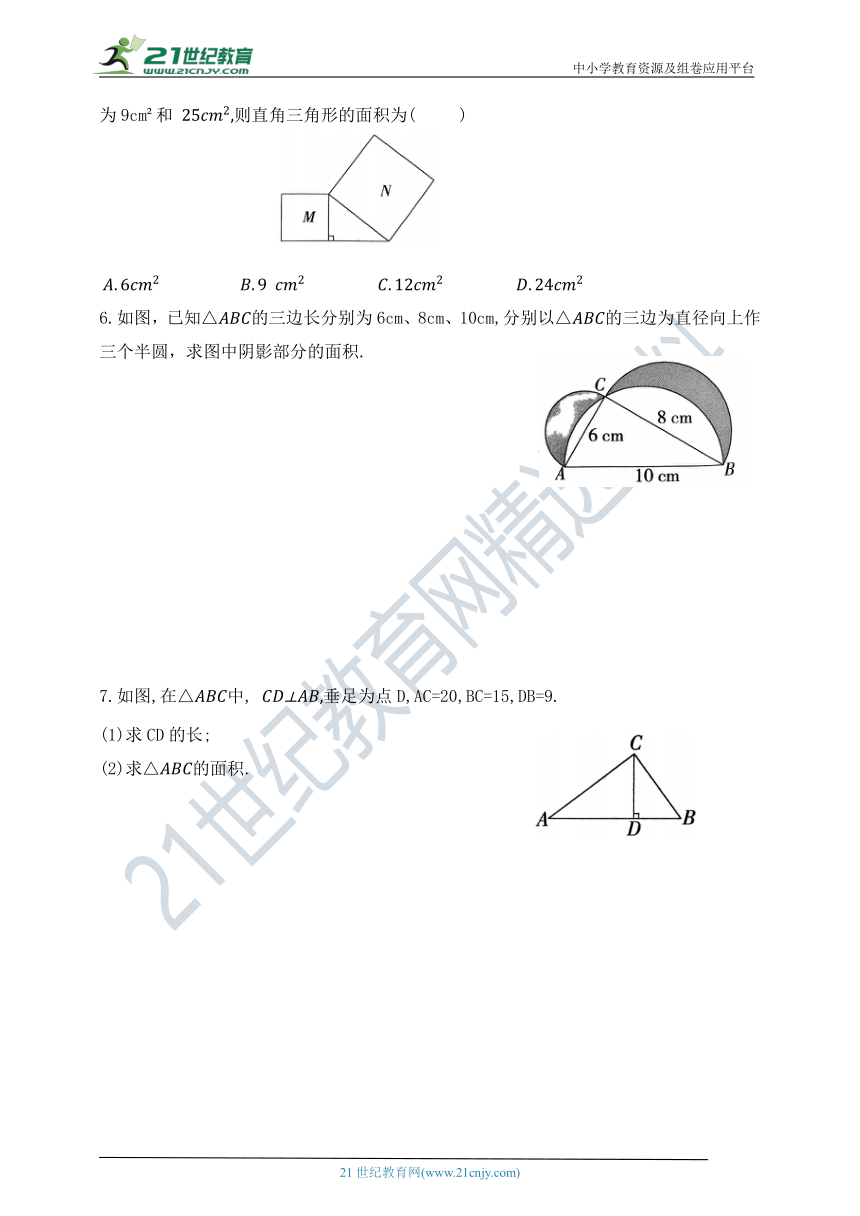
5.如图,分别以直角三角形的一条直角边和斜边为边作正方形M和N,它们的面积分别为9cm 和 则直角三角形的面积为( )
6.如图,已知△的三边长分别为6cm、8cm、10cm,分别以△的三边为直径向上作三个半圆,求图中阴影部分的面积.
7.如图,在△中, 垂足为点D,AC=20,BC=15,DB=9.
(1)求CD的长;
(2)求△的面积.
类型五 在探究动点的存在性问题中的应用
8.如图,在 中,∠ACB=90°,AB=20cm,AC=16cm,点P为线段AC上一动点,点P从点A出发,以每秒1cm的速度向点C运动,连接PB,设运动时间为t秒(t
(1)当△PBC的面积为△的面积的一半时,求t的值;
(2)当t为何值时,AP=PB
参考答案
1.答案 等腰直角三角形
解析 因为 所以 所以 所以△为等腰直角三角形.
2.C 因为甲、乙两艘客轮同时离开港口0,航行速度都是40米/分钟,甲客轮用30分钟到达A处,乙客轮用40分钟到达B处,所以甲客轮航行的路程为 米,乙客轮航行的路程为 1600米,因为A、B之间的距离为2000米,且所以 因为甲客轮沿着北偏东 方向航行,所以乙客轮沿着南偏东 或北偏西 方向航行,故选C.
3.C 在 中, ∵AE为△的角平分线,
∵ED⊥AB,∴∠EDA=90°,∴∠EDA=∠ECA,又
故选C.
4.解析 如图所示,将三级台阶的台阶面展平后得到一个长方形,长为20dm,宽为 15(dm),则 所以 25dm,故蚂蚁沿台阶面爬到B点的最短路程为25 dm.
5.A 如图, ∴
∴直角三角形的面积 故选A.
6.解析 因为 所以 所以△为直角三角形, =90°,所以△ABC的面积
以BC为直径的半圆的面积是 ,以AC为直径的半圆的面积是
以AB为直径的半圆的面积是
所以题图中阴影部分的面积是
7.解析 在中,
∴CD
(2)在Rt△ADC中,
8.解析 (1)由题意得
当BP是△的中线时,△的面积为△的面积的一半,所以 所以
(2)在 中, 16cm,由勾股定理得 因为 所以 在 中, 当 时, 即 解得 所以当 时,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专项训练
勾股定理及直角三角形的判别条件
类型一 判断三角形的形状
1.已知a,b,c是△ABC的三边长,且满足 ,则△ABC的形状为_____________.
类型二 说明线段垂直
2.甲、乙两艘客轮同时离开港口O,航行速度都是40米/分钟,甲客轮用30分钟到达A处,乙客轮用40分钟到达B处.若A、B之间的距离为2000米,甲客轮沿着北偏东30°方向航行,则乙客轮的航行方向可能是( )
A.北偏西30° B.南偏西30° C.南偏东60° D.南偏西60°
类型三 求线段的长
3.如图,在Rt△ABC中,∠ACB=90°,AE为△ABC的角平分线,ED⊥AB,若AC=6,BC=8,则BD的长为( )
A.2 B.3 C.4 D.5
4.如图是一个三级台阶,它的每一级的长、宽、高分别为20dm,3dm,2dm,A和B是这个台阶两个相对的端点,A点处有一只蚂蚁,想到B点吃可口的食物,求蚂蚁沿着台阶面爬到B点的最短路程.
类型四 求图形的面积
5.如图,分别以直角三角形的一条直角边和斜边为边作正方形M和N,它们的面积分别为9cm 和 则直角三角形的面积为( )
6.如图,已知△的三边长分别为6cm、8cm、10cm,分别以△的三边为直径向上作三个半圆,求图中阴影部分的面积.
7.如图,在△中, 垂足为点D,AC=20,BC=15,DB=9.
(1)求CD的长;
(2)求△的面积.
类型五 在探究动点的存在性问题中的应用
8.如图,在 中,∠ACB=90°,AB=20cm,AC=16cm,点P为线段AC上一动点,点P从点A出发,以每秒1cm的速度向点C运动,连接PB,设运动时间为t秒(t
(1)当△PBC的面积为△的面积的一半时,求t的值;
(2)当t为何值时,AP=PB
参考答案
1.答案 等腰直角三角形
解析 因为 所以 所以 所以△为等腰直角三角形.
2.C 因为甲、乙两艘客轮同时离开港口0,航行速度都是40米/分钟,甲客轮用30分钟到达A处,乙客轮用40分钟到达B处,所以甲客轮航行的路程为 米,乙客轮航行的路程为 1600米,因为A、B之间的距离为2000米,且所以 因为甲客轮沿着北偏东 方向航行,所以乙客轮沿着南偏东 或北偏西 方向航行,故选C.
3.C 在 中, ∵AE为△的角平分线,
∵ED⊥AB,∴∠EDA=90°,∴∠EDA=∠ECA,又
故选C.
4.解析 如图所示,将三级台阶的台阶面展平后得到一个长方形,长为20dm,宽为 15(dm),则 所以 25dm,故蚂蚁沿台阶面爬到B点的最短路程为25 dm.
5.A 如图, ∴
∴直角三角形的面积 故选A.
6.解析 因为 所以 所以△为直角三角形, =90°,所以△ABC的面积
以BC为直径的半圆的面积是 ,以AC为直径的半圆的面积是
以AB为直径的半圆的面积是
所以题图中阴影部分的面积是
7.解析 在中,
∴CD
(2)在Rt△ADC中,
8.解析 (1)由题意得
当BP是△的中线时,△的面积为△的面积的一半,所以 所以
(2)在 中, 16cm,由勾股定理得 因为 所以 在 中, 当 时, 即 解得 所以当 时,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
