北师大版九年级上册第六章 反比例函数学案(word版无答案)
文档属性
| 名称 | 北师大版九年级上册第六章 反比例函数学案(word版无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 615.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-19 14:47:40 | ||
图片预览


文档简介
反比例函数
【知识点1】反比例函数的定义
定义:一般地,形如(为常数,)的函数称为反比例函数。还可以写成,(为常数,)
反比例函数解析式的特征:
⑴等号左边是函数,等号右边是一个分式。分子是不为零的常数(也叫做比例系数),分母中含有自变量,且指数为1.
⑵比例系数
⑶自变量的取值为一切非零实数。
⑷函数的取值是一切非零实数。
【经典例题】
例1、下列等式中,哪些是反比例函数
(1) (2) (3) (4) (5)
(6) (7)
例2、若与成反比例,与成正比例,则是的( )
A、正比例函数 B、反比例函数 C、一次函数 D、不能确定
例3、当m取什么值时,函数是反比例函数?
【小试牛刀】
1、苹果每千克元,花10元钱可买千克的苹果,则与之间的函数关系式为
2、若函数是反比例函数,则m的取值是
3、函数中自变量的取值范围是
【知识点2】知识点2、待定系数法求反比例函数解析式
例1、已知与的反比例函数,当时,
(1)写出与之间的函数解析式;
(2)求当时的值.
例2、已知函数,与成正比例,与成反比例,且当时,;当时,
(1)求与的函数关系式
(2)当时,求函数的值
例3、已知反比例函数的图象经过点,点的坐标为,点的纵坐标为1,点的纵坐标为2,
(1)求该反比例函数的解析式;
(2)求、点的坐标。
【知识点3】反比例函数的图像及性质
1、画函数图象的基本步骤——列表、描点、连线
注意:
(1)列表取值时,因为,函数无意义,因此可以以“0”为中心,对称性取值,
即正负数各取一样,且互为相反数,这样便于求y的值。
(2)因为图象的样子不太清楚,应该多取一些值、多描一些点,这样便于连线,使画出的图象更精确。
(3)连线时应接自变量的值从小到大的顺序用平滑的曲线连接,切忌用折线。
(4)因为X≠0,K≠0,所以y≠0,从而决定反比例函数图象不可能与坐标轴相交 ,两象限内的部分只能“隔海相望”,形成两个分支。
【巩固练习】
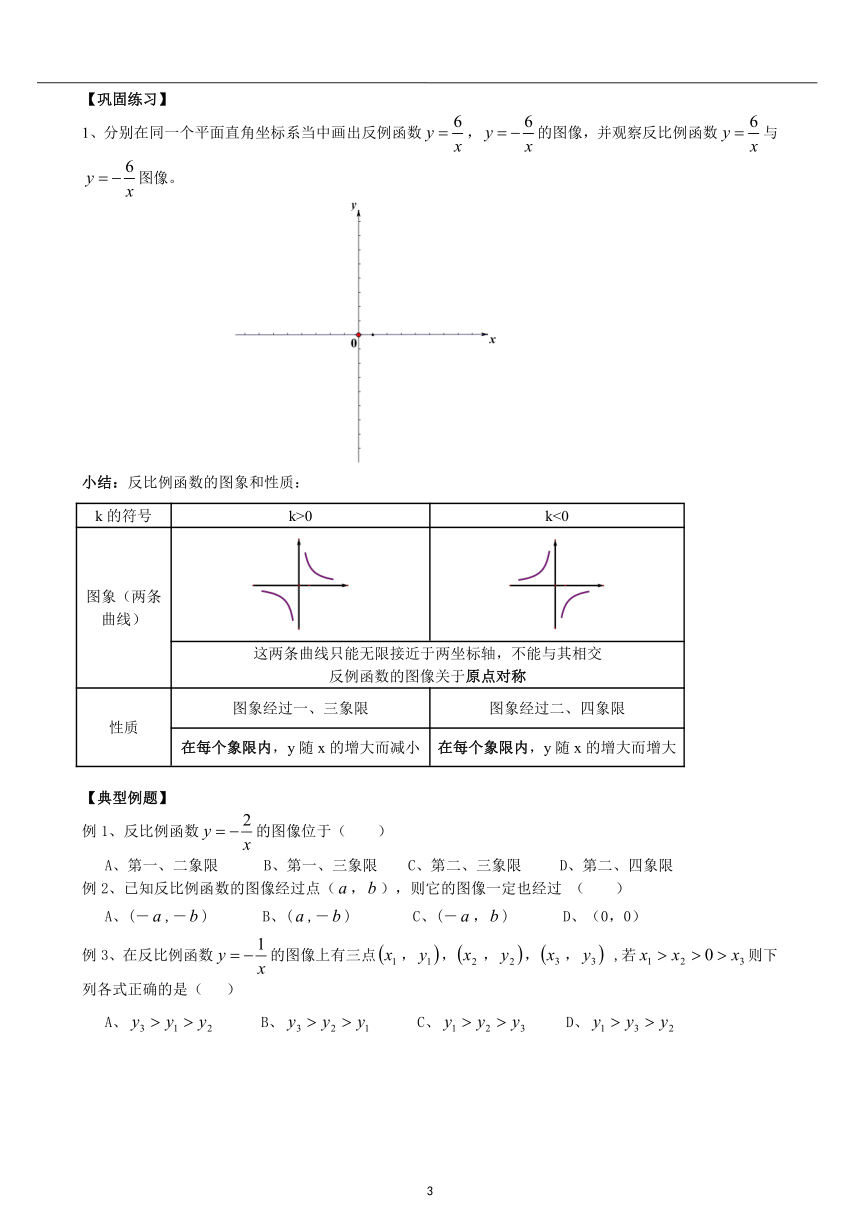
1、分别在同一个平面直角坐标系当中画出反例函数,的图像,并观察反比例函数与图像。
小结:反比例函数的图象和性质:
k的符号 k>0 k<0
图象(两条曲线)
这两条曲线只能无限接近于两坐标轴,不能与其相交反例函数的图像关于原点对称
性质 图象经过一、三象限 图象经过二、四象限
在每个象限内,y随x的增大而减小 在每个象限内,y随x的增大而增大
【典型例题】
例1、反比例函数的图像位于( )
A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限
例2、已知反比例函数的图像经过点(,),则它的图像一定也经过 ( )
A、(-,-) B、(,-) C、(-,) D、(0,0)
例3、在反比例函数的图像上有三点,,,,, ,若则下列各式正确的是( )
A、 B、 C、 D、
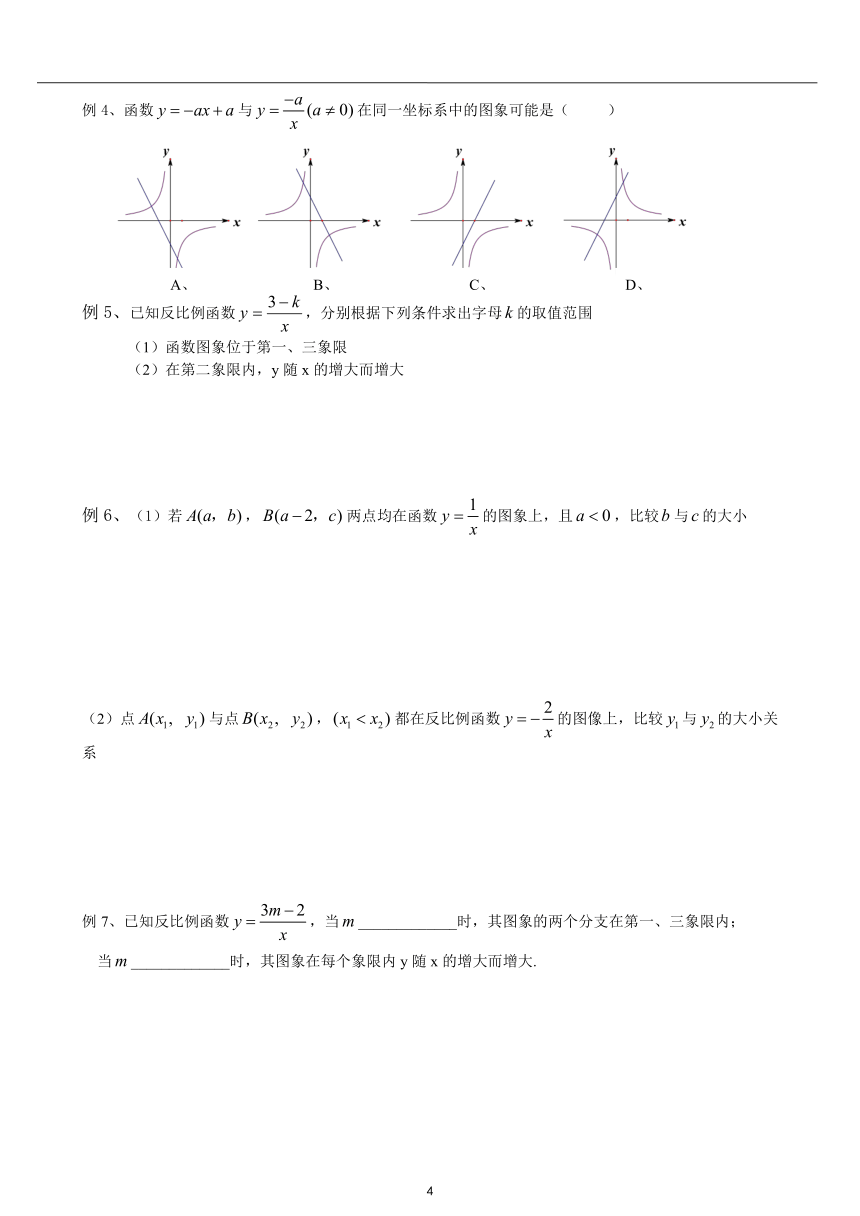
例4、函数与在同一坐标系中的图象可能是( )
例5、已知反比例函数,分别根据下列条件求出字母的取值范围
(1)函数图象位于第一、三象限
(2)在第二象限内,y随x的增大而增大
例6、(1)若,两点均在函数的图象上,且,比较与的大小
(2)点与点,都在反比例函数的图像上,比较与的大小关系
例7、已知反比例函数,当_____________时,其图象的两个分支在第一、三象限内;
当_____________时,其图象在每个象限内y随x的增大而增大.
【知识点4】反比例函数与一次函数的交点问题
(1)两个函数图像如果有交点,那么它们的交点坐标就是两个函数解析式联立方程组的解.
(2)要求函数图像的交点坐标,解方程组即可.
【典型例题】
例1、 已知一次函数的图象与反比例函数的图象相交,其中有一个交点的纵坐标为,求这两个函数的解析式.
【巩固练习】
1. 已知反比例函数与直线相交于A、B两点,A点的横坐标为,则两函数图象另一个交点B的坐标为
2. 已知反比例函数与一次函数的图象的一个交点的纵坐标是,则的值为 .
3.已知一次函数与反比例函数的图像有两个交点。当为何值时,有一个交点的纵坐标为6
【知识点5】知识点3、用函数的方法解决方程、不等式的有关问题
例1如图,是一次函数与反比例函数的图象,则关于x的方程的解为( ).
A、 B、
C、 D、
例2、如图,一次函数的图象与反比例函数的图象交于、两点.
(1)求两个函数的解析式;
(2)根据图象写出使一次函数值大于反比例函数值的自变量的取值范围.
【巩固练习】
1. 如图,已知,是一次函数的图象和反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的解析式
(2)求直线与轴的交点的坐标及△的面积;
(3)求方程的解(请直接写出答案);
(4)求不等式的解集(请直接写出答案).
2.函数与(,为非零常数)的图象的如图所示,由图象可知:关于的不等式的
解集是( )
A. B.
C.或 D.或
3.已知反比例函数和一次函数的图象都经.
(1)求点P的坐标和两个函数的解析式;
(2)若点、是反比例函数图象上的点,请比较y1与y2.
4. 已知一次函数的图象与反比例函数的图象交于第四象限的一点.
(1)求这个反比例函数的解析式.
(2)当时,求的取值范围是多少
【课后练习】
1、函数的图象与直线没有交点,那么k的取值范围是( )
A、 B、 C、 D、
2、函数y1=x(x≥0),y2=(x>0)的图象如图所示,下列结论:
①两函数图象的交点坐标为A(2,2);
②当x>2时,y2>y1;
③直线x=1分别与两函数图象相交于B、C两点,则线段BC的长为3;
④当x逐渐增大时,y1的值随x的增大而增大,y2的值随x的增大减少.
其中正确的是( )
A.只有①② B.只有①③ C.只有②④ D.只有①③④
3、 如图,直线交坐标轴于A(-3,0)、B(0,5)两点,则不等式的解集为( )
A. B. C. D.
4、如图,已知双曲线经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(,4),则△AOC的面积为( )
A.12 B.9 C.6 D.4
5、如图,直线与双曲线交于A、B两点,过点A作AM⊥轴,垂足为M,连结BM,若=2,则的值是( )
A、2 B、m-2 C、m D、4
6、如图,直线与双曲线相交于A(2,1)、B两点.
(1)求m及k的值;
(2)不解关于x、y的方程组直接写出点B的坐标,当为何值时,一次函数的函数值大于反比例函数的函数值;
(3)直线经过点B吗?请说明理由.
【知识点6】实际问题与反比例函数
1.求函数解析式的方法:
(1)用待定系数法.
(2)根据实际意义列函数解析式.(自变量的取值范围)
2.注意学科间综合,但重点放在对数学知识的研究上,对跨学科问题不会过难.
【典型例题】
例1.近视眼镜的度数y(度)与镜片焦距x(米)成反比例.已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数y与镜片焦距x之间的函数解析式是_____ _______.
【巩固】
1、用电器的输出功率与通过的电流、用电器的电阻之间的关系是,下面说法正确的是( )
A.为定值,与成反比例 B.为定值,与成反比例
C.为定值,与成正比例 D.为定值,与成正比例
2、在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度(单位:kg/m3)是体积(单位:m3)的反比例函数,它的图象如图3所示,当时,气体的密度是( )
A.5kg/m3 B.2kg/m3 C.100kg/m3 D,1kg/m3
INCLUDEPICTURE "../四大/" \* MERGEFORMAT
3、一块蓄电池的电压为定值,使用此蓄电池为电源时,电流(A)与电阻(Ω)之间的函数关系如图所示,如果以此蓄电池为电源的用电器限制电流不得超过10A,那么此用电器的可变电阻应( )
A.不小于4.8Ω B.不大于4.8Ω C.不小于14Ω D.不大于14Ω
D、
C、
B、
A、
y
y1=x
y2=
x
6
O
R/Ω
I/A
8
1
【知识点1】反比例函数的定义
定义:一般地,形如(为常数,)的函数称为反比例函数。还可以写成,(为常数,)
反比例函数解析式的特征:
⑴等号左边是函数,等号右边是一个分式。分子是不为零的常数(也叫做比例系数),分母中含有自变量,且指数为1.
⑵比例系数
⑶自变量的取值为一切非零实数。
⑷函数的取值是一切非零实数。
【经典例题】
例1、下列等式中,哪些是反比例函数
(1) (2) (3) (4) (5)
(6) (7)
例2、若与成反比例,与成正比例,则是的( )
A、正比例函数 B、反比例函数 C、一次函数 D、不能确定
例3、当m取什么值时,函数是反比例函数?
【小试牛刀】
1、苹果每千克元,花10元钱可买千克的苹果,则与之间的函数关系式为
2、若函数是反比例函数,则m的取值是
3、函数中自变量的取值范围是
【知识点2】知识点2、待定系数法求反比例函数解析式
例1、已知与的反比例函数,当时,
(1)写出与之间的函数解析式;
(2)求当时的值.
例2、已知函数,与成正比例,与成反比例,且当时,;当时,
(1)求与的函数关系式
(2)当时,求函数的值
例3、已知反比例函数的图象经过点,点的坐标为,点的纵坐标为1,点的纵坐标为2,
(1)求该反比例函数的解析式;
(2)求、点的坐标。
【知识点3】反比例函数的图像及性质
1、画函数图象的基本步骤——列表、描点、连线
注意:
(1)列表取值时,因为,函数无意义,因此可以以“0”为中心,对称性取值,
即正负数各取一样,且互为相反数,这样便于求y的值。
(2)因为图象的样子不太清楚,应该多取一些值、多描一些点,这样便于连线,使画出的图象更精确。
(3)连线时应接自变量的值从小到大的顺序用平滑的曲线连接,切忌用折线。
(4)因为X≠0,K≠0,所以y≠0,从而决定反比例函数图象不可能与坐标轴相交 ,两象限内的部分只能“隔海相望”,形成两个分支。
【巩固练习】
1、分别在同一个平面直角坐标系当中画出反例函数,的图像,并观察反比例函数与图像。
小结:反比例函数的图象和性质:
k的符号 k>0 k<0
图象(两条曲线)
这两条曲线只能无限接近于两坐标轴,不能与其相交反例函数的图像关于原点对称
性质 图象经过一、三象限 图象经过二、四象限
在每个象限内,y随x的增大而减小 在每个象限内,y随x的增大而增大
【典型例题】
例1、反比例函数的图像位于( )
A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限
例2、已知反比例函数的图像经过点(,),则它的图像一定也经过 ( )
A、(-,-) B、(,-) C、(-,) D、(0,0)
例3、在反比例函数的图像上有三点,,,,, ,若则下列各式正确的是( )
A、 B、 C、 D、
例4、函数与在同一坐标系中的图象可能是( )
例5、已知反比例函数,分别根据下列条件求出字母的取值范围
(1)函数图象位于第一、三象限
(2)在第二象限内,y随x的增大而增大
例6、(1)若,两点均在函数的图象上,且,比较与的大小
(2)点与点,都在反比例函数的图像上,比较与的大小关系
例7、已知反比例函数,当_____________时,其图象的两个分支在第一、三象限内;
当_____________时,其图象在每个象限内y随x的增大而增大.
【知识点4】反比例函数与一次函数的交点问题
(1)两个函数图像如果有交点,那么它们的交点坐标就是两个函数解析式联立方程组的解.
(2)要求函数图像的交点坐标,解方程组即可.
【典型例题】
例1、 已知一次函数的图象与反比例函数的图象相交,其中有一个交点的纵坐标为,求这两个函数的解析式.
【巩固练习】
1. 已知反比例函数与直线相交于A、B两点,A点的横坐标为,则两函数图象另一个交点B的坐标为
2. 已知反比例函数与一次函数的图象的一个交点的纵坐标是,则的值为 .
3.已知一次函数与反比例函数的图像有两个交点。当为何值时,有一个交点的纵坐标为6
【知识点5】知识点3、用函数的方法解决方程、不等式的有关问题
例1如图,是一次函数与反比例函数的图象,则关于x的方程的解为( ).
A、 B、
C、 D、
例2、如图,一次函数的图象与反比例函数的图象交于、两点.
(1)求两个函数的解析式;
(2)根据图象写出使一次函数值大于反比例函数值的自变量的取值范围.
【巩固练习】
1. 如图,已知,是一次函数的图象和反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的解析式
(2)求直线与轴的交点的坐标及△的面积;
(3)求方程的解(请直接写出答案);
(4)求不等式的解集(请直接写出答案).
2.函数与(,为非零常数)的图象的如图所示,由图象可知:关于的不等式的
解集是( )
A. B.
C.或 D.或
3.已知反比例函数和一次函数的图象都经.
(1)求点P的坐标和两个函数的解析式;
(2)若点、是反比例函数图象上的点,请比较y1与y2.
4. 已知一次函数的图象与反比例函数的图象交于第四象限的一点.
(1)求这个反比例函数的解析式.
(2)当时,求的取值范围是多少
【课后练习】
1、函数的图象与直线没有交点,那么k的取值范围是( )
A、 B、 C、 D、
2、函数y1=x(x≥0),y2=(x>0)的图象如图所示,下列结论:
①两函数图象的交点坐标为A(2,2);
②当x>2时,y2>y1;
③直线x=1分别与两函数图象相交于B、C两点,则线段BC的长为3;
④当x逐渐增大时,y1的值随x的增大而增大,y2的值随x的增大减少.
其中正确的是( )
A.只有①② B.只有①③ C.只有②④ D.只有①③④
3、 如图,直线交坐标轴于A(-3,0)、B(0,5)两点,则不等式的解集为( )
A. B. C. D.
4、如图,已知双曲线经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(,4),则△AOC的面积为( )
A.12 B.9 C.6 D.4
5、如图,直线与双曲线交于A、B两点,过点A作AM⊥轴,垂足为M,连结BM,若=2,则的值是( )
A、2 B、m-2 C、m D、4
6、如图,直线与双曲线相交于A(2,1)、B两点.
(1)求m及k的值;
(2)不解关于x、y的方程组直接写出点B的坐标,当为何值时,一次函数的函数值大于反比例函数的函数值;
(3)直线经过点B吗?请说明理由.
【知识点6】实际问题与反比例函数
1.求函数解析式的方法:
(1)用待定系数法.
(2)根据实际意义列函数解析式.(自变量的取值范围)
2.注意学科间综合,但重点放在对数学知识的研究上,对跨学科问题不会过难.
【典型例题】
例1.近视眼镜的度数y(度)与镜片焦距x(米)成反比例.已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数y与镜片焦距x之间的函数解析式是_____ _______.
【巩固】
1、用电器的输出功率与通过的电流、用电器的电阻之间的关系是,下面说法正确的是( )
A.为定值,与成反比例 B.为定值,与成反比例
C.为定值,与成正比例 D.为定值,与成正比例
2、在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度(单位:kg/m3)是体积(单位:m3)的反比例函数,它的图象如图3所示,当时,气体的密度是( )
A.5kg/m3 B.2kg/m3 C.100kg/m3 D,1kg/m3
INCLUDEPICTURE "../四大/" \* MERGEFORMAT
3、一块蓄电池的电压为定值,使用此蓄电池为电源时,电流(A)与电阻(Ω)之间的函数关系如图所示,如果以此蓄电池为电源的用电器限制电流不得超过10A,那么此用电器的可变电阻应( )
A.不小于4.8Ω B.不大于4.8Ω C.不小于14Ω D.不大于14Ω
D、
C、
B、
A、
y
y1=x
y2=
x
6
O
R/Ω
I/A
8
1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
