【核心素养目标】24.2.2 直线和圆的位置关系(3) 教案
文档属性
| 名称 | 【核心素养目标】24.2.2 直线和圆的位置关系(3) 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-20 07:56:12 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
24.2.2 直线和圆的位置关系(3) 教学设计
课题 24.2.2 直线和圆的位置关系(3) 单元 第24单元 学科 数学 年级 九年级(上)
教材分析 为证明线段相等、角相等提供新的方法.解决有关圆的切线长问题时,往往需要我们构建基本图形。(1)分别连结圆心和切点(2)连结两切点(3)连结圆心和圆外一点.
核心素养分析 切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据.必须掌握并能灵活应用.培养几何直观和推理能力等核心素养.
学习目标 1. 掌握切线长的定义及切线长定理;
2. 运用切线长定理进行计算与证明;3. 掌握三角形的内切圆和内心.
重点 运用切线长定理进行计算与证明。
难点 掌握三角形的内切圆和内心。
教学过程
教学环节 教师活动 学生活动 设计意图
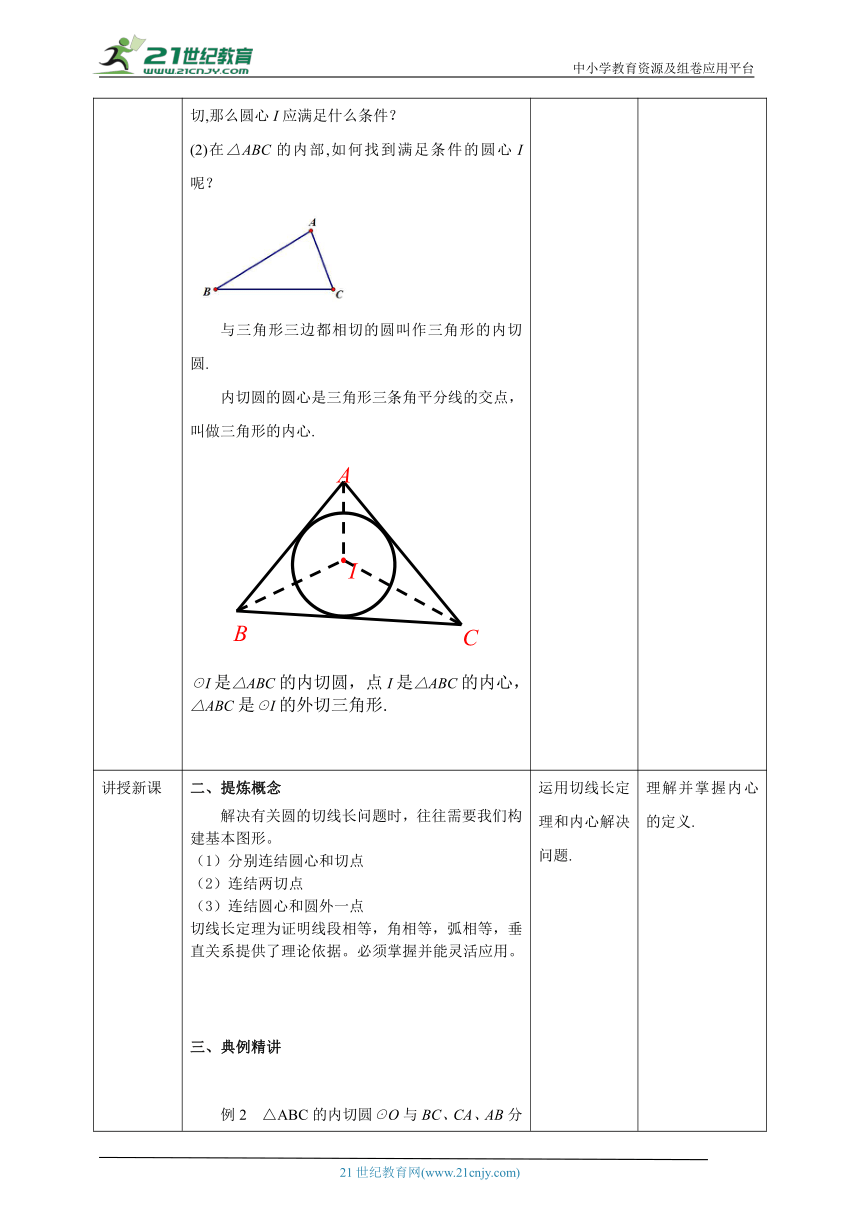
导入新课 一、创设情景,引出课题环节一:探究切线长定理问题:过圆外的一点作圆的切线,可以作几条?两条切线长: 切线上一点到切点之间的线段的长叫作这点到圆的切线长.思考:切线长与切线的区别?①切线是直线,不能度量.②切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.探究:已知PA、PB为⊙O两条切线,切点分别为A、B,沿着直线OP把圆对折,PA与PB,∠OPA与∠OPB有什么关系 PA=PB,∠OPA=∠OPB你能证明此结论吗?证明:连接OA、OB∵PA、PB为⊙O两条切线∴OA⊥PA,OB⊥PB∵OA=OB,OP=OP∴Rt△AOP≌Rt△BOP∴PA=PB,∠OPA=∠OPB探究:已知PA、PB为⊙O两条切线,切点分别为A、B,沿着直线OP把圆对折,还有其他结论成立吗 OP垂直平分AB切线长定理: 从圆外一点引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角. 几何语言:∵PA、PB分别切⊙O于A、B,∴PA=PB,∠OPA=∠OPB.为证明线段相等、角相等提供新的方法.环节三:探究内切圆思考:如何在三角形内部画一个圆,使它与已知三角形的三边都相切?分析:(1)如果半径为r的☉I与△ABC的三边都相切,那么圆心I应满足什么条件?(2)在△ABC的内部,如何找到满足条件的圆心I呢?与三角形三边都相切的圆叫作三角形的内切圆.内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.☉I是△ABC的内切圆,点I是△ABC的内心,△ABC是☉I的外切三角形. 思考自议通过探究,发现切线长定理,并进行总结. 鼓励学生通过自学探究得出结论.
讲授新课 二、提炼概念解决有关圆的切线长问题时,往往需要我们构建基本图形。(1)分别连结圆心和切点(2)连结两切点(3)连结圆心和圆外一点切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用。三、典例精讲例2 △ABC的内切圆☉O与BC、CA、AB分别相切于点D、E、F,且AB=9,BC=14,CA=13,求AF、BD、CE的长.解:设AF=x,则AE=x,CD=CE=AC-AE=13-x,BD=BF =AB -AF=9-x.由BD+CD=BC,可得(13-x)+(9-x)=14,解得x=4.∴AF=4,BD=5,CE=9.小结:运用切线长定理,将相等线段转化集中到某条边上,从而建立方程. 运用切线长定理和内心解决问题. 理解并掌握内心的定义.
课堂练习 四、巩固训练1.如图,PA切⊙O于点A,PB切⊙O于点B,下列结论中,错误的是( ) A.∠APO =∠BPO B.PA = PB C.AB ⊥OP D.PA = P0 D2.如图,PA、PB是⊙O的两条切线,切点分别是A、B,如AP=4, ∠APB = 40 ° ,则∠APO = , PB = . 20 °,4如图,PA、PB是⊙O的两条切线,切点为A、B,∠P= 50 °,点C是⊙O上异于A、B的点,则∠ACB= . 65 °或115 °4.△ABC的内切圆⊙O与三边分别切于D、E、F三点,如图,已知AF=3, BD+CE=12, 则△ABC的周长是 .245.△ABC的内切圆半径为r,△ABC的周长为l,求△ABC的面积. (提示:设内心为O,连接OA、OB、OC)解:如图, 设三个切点分别为D,E,F.连接OD, OE, OF. S△AOB = S△AOB + S△BOC + S△AOC = 1/2×AB×r+ 1/2×BC×r+ 1/2×AC×r = 1/2×(AB +BC +AC )×r = 1/2 l r 6.如图,某镇在进入镇区的道路交叉口的三角地处建造了一座镇标雕塑,以树立起文明古镇的形象. 已知雕塑中心M到道路三边AC、BC、AB的距离相等,AC⊥BC,BC=30米,AC=40米. 请你帮助计算一下,镇标雕塑中心M离道路三边的距离有多远?证明:过点M作MD⊥AC,ME⊥BC,MF⊥AB由题意知MD=ME=MF∵AC⊥CB ∴∠C=90° 在Rt△ABC中,根据勾股定理的∴MD=ME=MF=10(米)
课堂小结
O
P
A
B
O
P
A
B
B
A
C
I
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
24.2.2 直线和圆的位置关系(3) 教学设计
课题 24.2.2 直线和圆的位置关系(3) 单元 第24单元 学科 数学 年级 九年级(上)
教材分析 为证明线段相等、角相等提供新的方法.解决有关圆的切线长问题时,往往需要我们构建基本图形。(1)分别连结圆心和切点(2)连结两切点(3)连结圆心和圆外一点.
核心素养分析 切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据.必须掌握并能灵活应用.培养几何直观和推理能力等核心素养.
学习目标 1. 掌握切线长的定义及切线长定理;
2. 运用切线长定理进行计算与证明;3. 掌握三角形的内切圆和内心.
重点 运用切线长定理进行计算与证明。
难点 掌握三角形的内切圆和内心。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题环节一:探究切线长定理问题:过圆外的一点作圆的切线,可以作几条?两条切线长: 切线上一点到切点之间的线段的长叫作这点到圆的切线长.思考:切线长与切线的区别?①切线是直线,不能度量.②切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.探究:已知PA、PB为⊙O两条切线,切点分别为A、B,沿着直线OP把圆对折,PA与PB,∠OPA与∠OPB有什么关系 PA=PB,∠OPA=∠OPB你能证明此结论吗?证明:连接OA、OB∵PA、PB为⊙O两条切线∴OA⊥PA,OB⊥PB∵OA=OB,OP=OP∴Rt△AOP≌Rt△BOP∴PA=PB,∠OPA=∠OPB探究:已知PA、PB为⊙O两条切线,切点分别为A、B,沿着直线OP把圆对折,还有其他结论成立吗 OP垂直平分AB切线长定理: 从圆外一点引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角. 几何语言:∵PA、PB分别切⊙O于A、B,∴PA=PB,∠OPA=∠OPB.为证明线段相等、角相等提供新的方法.环节三:探究内切圆思考:如何在三角形内部画一个圆,使它与已知三角形的三边都相切?分析:(1)如果半径为r的☉I与△ABC的三边都相切,那么圆心I应满足什么条件?(2)在△ABC的内部,如何找到满足条件的圆心I呢?与三角形三边都相切的圆叫作三角形的内切圆.内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.☉I是△ABC的内切圆,点I是△ABC的内心,△ABC是☉I的外切三角形. 思考自议通过探究,发现切线长定理,并进行总结. 鼓励学生通过自学探究得出结论.
讲授新课 二、提炼概念解决有关圆的切线长问题时,往往需要我们构建基本图形。(1)分别连结圆心和切点(2)连结两切点(3)连结圆心和圆外一点切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用。三、典例精讲例2 △ABC的内切圆☉O与BC、CA、AB分别相切于点D、E、F,且AB=9,BC=14,CA=13,求AF、BD、CE的长.解:设AF=x,则AE=x,CD=CE=AC-AE=13-x,BD=BF =AB -AF=9-x.由BD+CD=BC,可得(13-x)+(9-x)=14,解得x=4.∴AF=4,BD=5,CE=9.小结:运用切线长定理,将相等线段转化集中到某条边上,从而建立方程. 运用切线长定理和内心解决问题. 理解并掌握内心的定义.
课堂练习 四、巩固训练1.如图,PA切⊙O于点A,PB切⊙O于点B,下列结论中,错误的是( ) A.∠APO =∠BPO B.PA = PB C.AB ⊥OP D.PA = P0 D2.如图,PA、PB是⊙O的两条切线,切点分别是A、B,如AP=4, ∠APB = 40 ° ,则∠APO = , PB = . 20 °,4如图,PA、PB是⊙O的两条切线,切点为A、B,∠P= 50 °,点C是⊙O上异于A、B的点,则∠ACB= . 65 °或115 °4.△ABC的内切圆⊙O与三边分别切于D、E、F三点,如图,已知AF=3, BD+CE=12, 则△ABC的周长是 .245.△ABC的内切圆半径为r,△ABC的周长为l,求△ABC的面积. (提示:设内心为O,连接OA、OB、OC)解:如图, 设三个切点分别为D,E,F.连接OD, OE, OF. S△AOB = S△AOB + S△BOC + S△AOC = 1/2×AB×r+ 1/2×BC×r+ 1/2×AC×r = 1/2×(AB +BC +AC )×r = 1/2 l r 6.如图,某镇在进入镇区的道路交叉口的三角地处建造了一座镇标雕塑,以树立起文明古镇的形象. 已知雕塑中心M到道路三边AC、BC、AB的距离相等,AC⊥BC,BC=30米,AC=40米. 请你帮助计算一下,镇标雕塑中心M离道路三边的距离有多远?证明:过点M作MD⊥AC,ME⊥BC,MF⊥AB由题意知MD=ME=MF∵AC⊥CB ∴∠C=90° 在Rt△ABC中,根据勾股定理的∴MD=ME=MF=10(米)
课堂小结
O
P
A
B
O
P
A
B
B
A
C
I
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
同课章节目录
