2021-2022 北师大版 数学 九年级下册 1.1.1 锐角三角函数 第1课时 课件(共39张PPT)
文档属性
| 名称 | 2021-2022 北师大版 数学 九年级下册 1.1.1 锐角三角函数 第1课时 课件(共39张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-19 17:50:20 | ||
图片预览




文档简介
(共39张PPT)
第一章 直角三角形的边角关系
1 锐角三角函数
第1课时
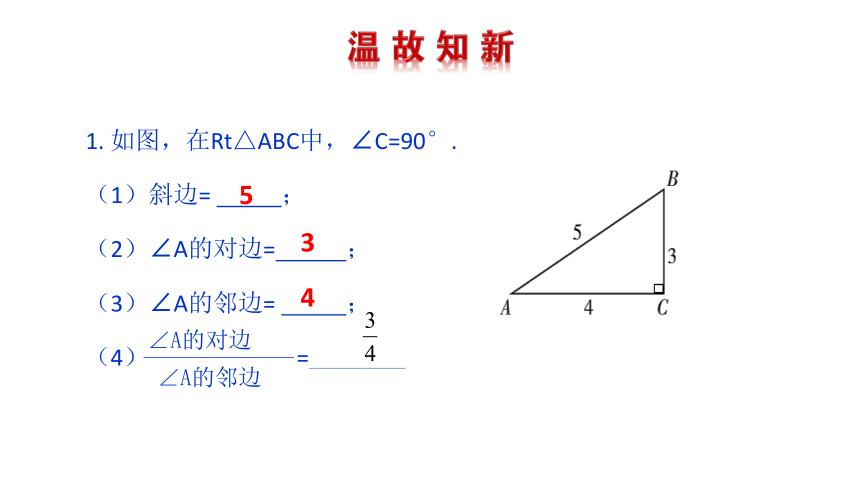
1. 如图,在Rt△ABC中,∠C=90°.
(1)斜边= ;
(2)∠A的对边= ;
(3)∠A的邻边= ;
(4) =_________
5
3
4
∠A的对边
∠A的邻边
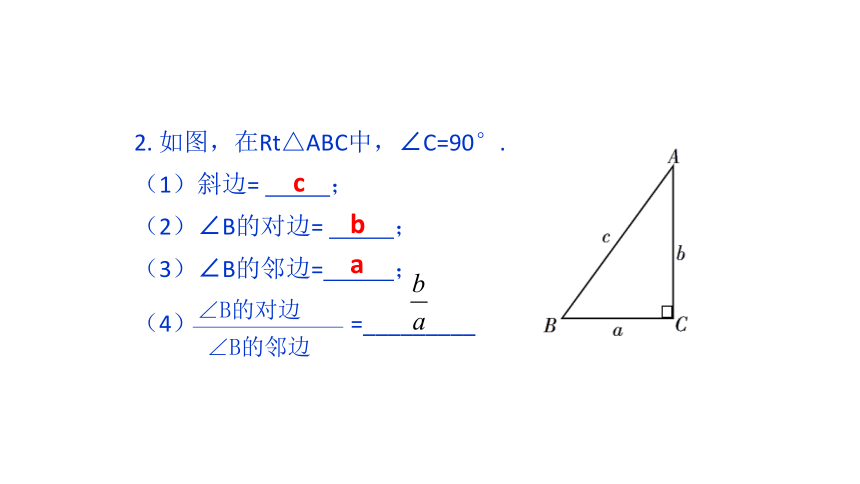
2. 如图,在Rt△ABC中,∠C=90°.
(1)斜边= ;
(2)∠B的对边= ;
(3)∠B的邻边= ;
(4) =_________
c
b
a
∠B的对边
∠B的邻边
1.经历探索直角三角形中边角关系的过程.理解正切的意义和与现实生活的联系.
2.能够用tan A表示直角三角形中两边的比,表示生活中物体的倾斜程度、坡度等,能够用正切进行简单的计算.
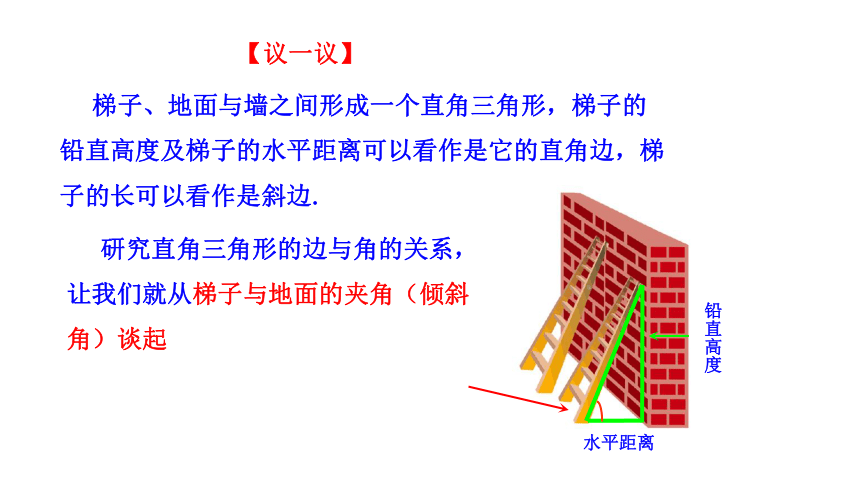
思考:衡量山“险”与“不险”的标准是什么呢?
梯子、地面与墙之间形成一个直角三角形,梯子的铅直高度及梯子的水平距离可以看作是它的直角边,梯子的长可以看作是斜边.
铅直高度
水平距离
研究直角三角形的边与角的关系,让我们就从梯子与地面的夹角(倾斜角)谈起
【议一议】
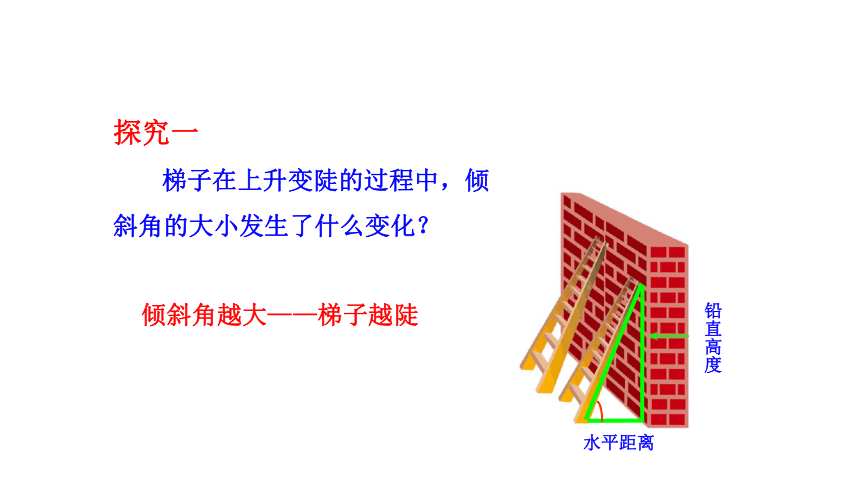
探究一
梯子在上升变陡的过程中,倾斜角的大小发生了什么变化?
倾斜角越大——梯子越陡
铅直高度
水平距离
用梯子的顶端放在墙上位置的高低及梯子的底端离墙的远近来判断.
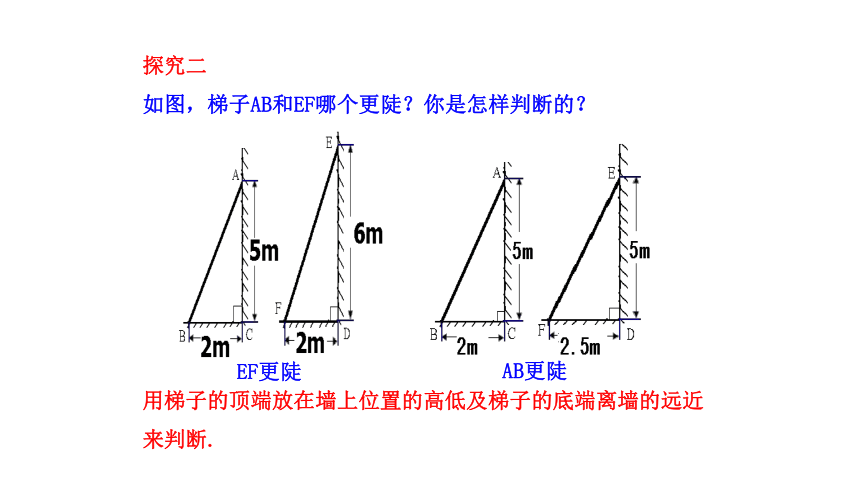
探究二
如图,梯子AB和EF哪个更陡?你是怎样判断的?
EF更陡
AB更陡
3m
3m
2m
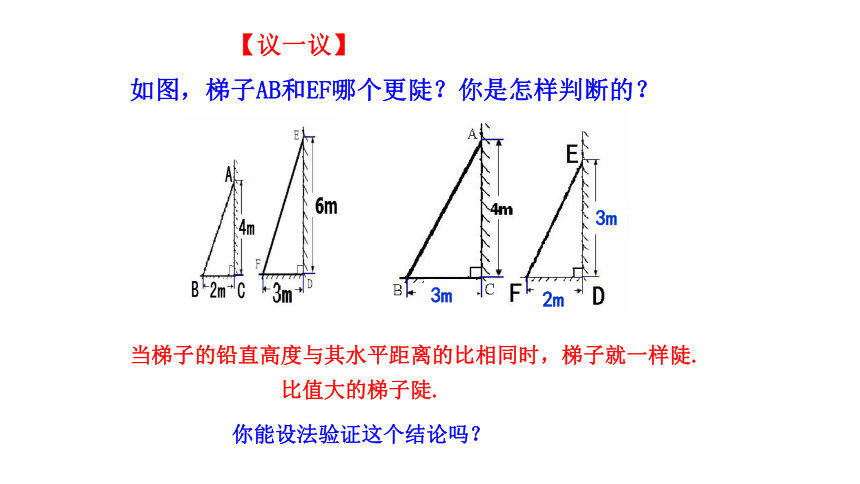
【议一议】
如图,梯子AB和EF哪个更陡?你是怎样判断的?
当梯子的铅直高度与其水平距离的比相同时,梯子就一样陡.
比值大的梯子陡.
你能设法验证这个结论吗?
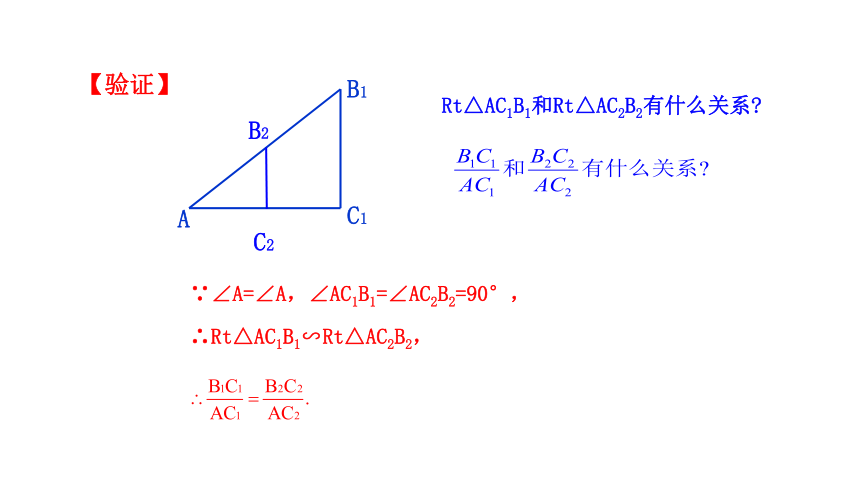
A
B1
C1
C2
B2
∵∠A=∠A,∠AC1B1=∠AC2B2=90°,
∴Rt△AC1B1∽Rt△AC2B2,
Rt△AC1B1和Rt△AC2B2有什么关系
【验证】
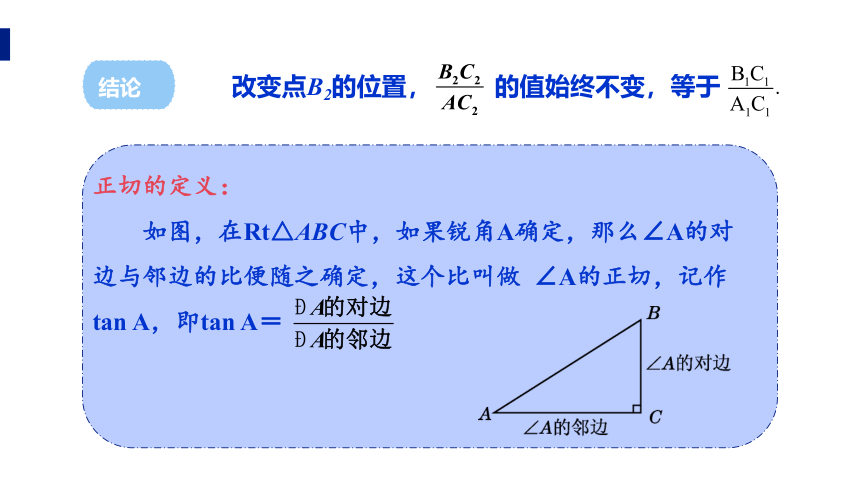
改变点B2的位置, 的值始终不变,等于
正切的定义:
如图,在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做 ∠A的正切,记作tan A,即tan A=
结论
C2
A
B1
C1
B2
B
1.如果任意改变B2在梯子上的位置呢 你有什么想法
∠A的大小确定, ∠A的对边与邻边的比值不变.
2.如果改变∠A 的大小, ∠A的对边与邻边的比值会随之改变吗
∠A的大小改变, ∠A的对边与邻边的比值会随之改变.
探究三
定义的几点说明:
1)初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角.
2) tanA是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”。但∠BAC的正切表示为:tan∠BAC,∠1的正切表示为:tan∠1.
3) tanA没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比(注意顺序).
4)tanA不表示“tan”乘以“A ”.
5) tanA的大小只与∠A的大小有关,而与直角三角形的边长无关
在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切(tangent).记作tan A 即
B
A
C
∠A的邻边
∠A的对边
tan A=
∠A的对边
∠A的邻边
【定义】
梯子AB的倾斜程度与tan A有关吗
tan A的值越大,梯子AB越陡.
A
B
C
【议一议】
例1:下图表示甲、乙两个自动扶梯,哪一个自动扶梯比较陡
解:甲梯中,
β
5m
┌
13m
4m
┐
8m
α
乙梯中,
因为tanα> tanβ,
所以甲梯更陡.
【例题】
(甲)
(乙)
一. 判断:
A
B
C
(1)
┍
A
B
C
7m
10m
(2)
4.如图 (2)
( ).
2.如图 (2)
( ).
3.如图 (2)
( ).
1. 如图 (1)
( ).
×
√
×
×
【跟踪训练】
二. 填空:
1.如图,tan =
tan =
2.如图, ∠ACB=90°,CD⊥AB.
tan∠ACD=_____
┌
A
C
B
D
A
B
C
B
A
tan B =_____=_____
正切也经常用来描述山坡的坡度.例如,有一山坡在水平方向上每前进100 m就升高60 m,那么山坡的坡度
就是
1.坡面与水平面的夹角(α)叫坡角.
2.坡面的铅直高度与水平宽度的比称为坡度
(或坡比),即坡度等于坡角的正切.
3.坡度越大,坡面越陡.
坡度与坡角
100m
60m
┌
α
例1 以下对坡度的描述正确的是( )
A.坡度是指倾斜角的度数
B.坡度是指斜坡的铅直高度与水平宽度的比
C.坡度是指斜坡的水平宽度与铅直高度的比
D.坡度是指斜坡的高度与斜坡长度的比
B
分析:概念不清,误以为坡度是一个角度,而猜测坡度即为倾斜角的度数.
【例题】
A
C
B
【解析】在Rt△ABC中,BC=20米,
∵坡度为1: ,
∴
则AC= 米.
又∵AB2=BC2+AC2,
例2.如图,拦水坝的坡度为 :1,若坝高BC=20米,求坝面AB的长.
【例题】
例3 如图,某人从山脚下的点A走了 200 m后到达山顶的点B,已知点B到山脚的 垂直距离为55 m,求山的坡度(结果精确到0.001).
B
解:由勾股定理可知,
AC= = ≈192.289(m),
∴tan ∠BAC= ≈ ≈0.286.
所以,山的坡度大约是0.286.
【例题】
A
,
2.如图,铁路路基横断面为一个四边形,其中AD∥BC.若两斜坡的坡度均为i=2∶3,上底宽是
3 m,路基高是4 m,则路基的下底宽是( )
A.7 m B.9 m
C.12 m D.15 m
D
1.在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切(tangent),记作:tan A
即tan A=
∠A的对边
∠A的邻边
B
A
C
∠A的对边
∠A的邻边
2.tan A的值越大,梯子越陡.对于山坡来说,正切对应的是坡度
1.tanA是在直角三角形中定义的,∠A是一个锐角(注意数形结合,构造直角三角形).
2.tanA是一个完整的符号,表示∠A的正切,习惯省去“∠”号(注意tanA不表示tan乘以A).
3.tanA是一个比值(直角边之比,注意比的顺序,且tanA﹥0,无单位).
4.tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则正切值相等;两锐角的正切值相等,则这两个锐角相等.
正切
定义
坡度
∠A越大,tanA越大,梯子越陡
与梯子倾斜程度的关系
1.在Rt△ABC中, ∠C=90o ,AC=12,BC=5,那么tan A等于( )
2.如图,下面四个梯子最陡的是( )
A B C D
C.
B.
D.
A.
B
C
3.河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡比是1: (坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是( )
A.5 米 B.10米 C.15米 D.10 米
【解析】∵BC:AC=1: ,
A
B
C
BC=5米,
∴AC=
A
4.小明沿着坡度为1:2的山坡向上走了1 000 m,则他升高了( )
A. B.500 m
C. D.1 000 m
【解析】设升高了x m,由勾股定理得,x2+(2x)2=(1000)2,解得x=
A
5.如图,为了测量河两岸A,B两点的距离,在与AB垂直的方向点C处测得AC=a,∠ACB=α,那么AB等于( )
A.a·sinα B.a·tanα
C.a·cosα D.
【解析】在Rt△ABC中,tanα=
所以AB= a·tanα
B
6. 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D,则tan∠BCD= .
7. 如图,在Rt△ABC中,AC=2,BC=1,则tan A= .
8.把△ABC三边的长度都扩大为原来的2倍,则锐角A的正切值( )
A.缩小为原来的 B.不变
C.扩大为原来的2倍 D.扩大为原来的4倍
B
【规律方法】当直角三角形的锐角确定后,它的对边与邻边的比值也随之确定;比值与三角形的大小无关,只与倾斜角的大小有关.
9.如图,△ABC的顶点都在正方形网格的格点上,则tanC的值为( )
A
【解析】设小正方形的边长为1.取AB与格点的交点为D,AC与格点的交点为E,则
10.如图, 位于6×6的方格纸中,
则 = .
A
B
C
=
A
B
C
D
E
11.如图,在一次数学课外实践活动中,要求测教学楼的高度AB.小刚在D处用高1.5 m的测角仪CD,测得教学楼顶端A的仰角为30°,然后向教学楼前进40 m到达E,又测得教学楼顶端A的仰角为60°.求这幢教学楼的高度AB.
【解析】在Rt△AFG中,
∴
∴
∴
答:这幢教学楼的高度AB为
m.
在Rt△ACG中,
第一章 直角三角形的边角关系
1 锐角三角函数
第1课时
1. 如图,在Rt△ABC中,∠C=90°.
(1)斜边= ;
(2)∠A的对边= ;
(3)∠A的邻边= ;
(4) =_________
5
3
4
∠A的对边
∠A的邻边
2. 如图,在Rt△ABC中,∠C=90°.
(1)斜边= ;
(2)∠B的对边= ;
(3)∠B的邻边= ;
(4) =_________
c
b
a
∠B的对边
∠B的邻边
1.经历探索直角三角形中边角关系的过程.理解正切的意义和与现实生活的联系.
2.能够用tan A表示直角三角形中两边的比,表示生活中物体的倾斜程度、坡度等,能够用正切进行简单的计算.
思考:衡量山“险”与“不险”的标准是什么呢?
梯子、地面与墙之间形成一个直角三角形,梯子的铅直高度及梯子的水平距离可以看作是它的直角边,梯子的长可以看作是斜边.
铅直高度
水平距离
研究直角三角形的边与角的关系,让我们就从梯子与地面的夹角(倾斜角)谈起
【议一议】
探究一
梯子在上升变陡的过程中,倾斜角的大小发生了什么变化?
倾斜角越大——梯子越陡
铅直高度
水平距离
用梯子的顶端放在墙上位置的高低及梯子的底端离墙的远近来判断.
探究二
如图,梯子AB和EF哪个更陡?你是怎样判断的?
EF更陡
AB更陡
3m
3m
2m
【议一议】
如图,梯子AB和EF哪个更陡?你是怎样判断的?
当梯子的铅直高度与其水平距离的比相同时,梯子就一样陡.
比值大的梯子陡.
你能设法验证这个结论吗?
A
B1
C1
C2
B2
∵∠A=∠A,∠AC1B1=∠AC2B2=90°,
∴Rt△AC1B1∽Rt△AC2B2,
Rt△AC1B1和Rt△AC2B2有什么关系
【验证】
改变点B2的位置, 的值始终不变,等于
正切的定义:
如图,在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做 ∠A的正切,记作tan A,即tan A=
结论
C2
A
B1
C1
B2
B
1.如果任意改变B2在梯子上的位置呢 你有什么想法
∠A的大小确定, ∠A的对边与邻边的比值不变.
2.如果改变∠A 的大小, ∠A的对边与邻边的比值会随之改变吗
∠A的大小改变, ∠A的对边与邻边的比值会随之改变.
探究三
定义的几点说明:
1)初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角.
2) tanA是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”。但∠BAC的正切表示为:tan∠BAC,∠1的正切表示为:tan∠1.
3) tanA没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比(注意顺序).
4)tanA不表示“tan”乘以“A ”.
5) tanA的大小只与∠A的大小有关,而与直角三角形的边长无关
在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切(tangent).记作tan A 即
B
A
C
∠A的邻边
∠A的对边
tan A=
∠A的对边
∠A的邻边
【定义】
梯子AB的倾斜程度与tan A有关吗
tan A的值越大,梯子AB越陡.
A
B
C
【议一议】
例1:下图表示甲、乙两个自动扶梯,哪一个自动扶梯比较陡
解:甲梯中,
β
5m
┌
13m
4m
┐
8m
α
乙梯中,
因为tanα> tanβ,
所以甲梯更陡.
【例题】
(甲)
(乙)
一. 判断:
A
B
C
(1)
┍
A
B
C
7m
10m
(2)
4.如图 (2)
( ).
2.如图 (2)
( ).
3.如图 (2)
( ).
1. 如图 (1)
( ).
×
√
×
×
【跟踪训练】
二. 填空:
1.如图,tan =
tan =
2.如图, ∠ACB=90°,CD⊥AB.
tan∠ACD=_____
┌
A
C
B
D
A
B
C
B
A
tan B =_____=_____
正切也经常用来描述山坡的坡度.例如,有一山坡在水平方向上每前进100 m就升高60 m,那么山坡的坡度
就是
1.坡面与水平面的夹角(α)叫坡角.
2.坡面的铅直高度与水平宽度的比称为坡度
(或坡比),即坡度等于坡角的正切.
3.坡度越大,坡面越陡.
坡度与坡角
100m
60m
┌
α
例1 以下对坡度的描述正确的是( )
A.坡度是指倾斜角的度数
B.坡度是指斜坡的铅直高度与水平宽度的比
C.坡度是指斜坡的水平宽度与铅直高度的比
D.坡度是指斜坡的高度与斜坡长度的比
B
分析:概念不清,误以为坡度是一个角度,而猜测坡度即为倾斜角的度数.
【例题】
A
C
B
【解析】在Rt△ABC中,BC=20米,
∵坡度为1: ,
∴
则AC= 米.
又∵AB2=BC2+AC2,
例2.如图,拦水坝的坡度为 :1,若坝高BC=20米,求坝面AB的长.
【例题】
例3 如图,某人从山脚下的点A走了 200 m后到达山顶的点B,已知点B到山脚的 垂直距离为55 m,求山的坡度(结果精确到0.001).
B
解:由勾股定理可知,
AC= = ≈192.289(m),
∴tan ∠BAC= ≈ ≈0.286.
所以,山的坡度大约是0.286.
【例题】
A
,
2.如图,铁路路基横断面为一个四边形,其中AD∥BC.若两斜坡的坡度均为i=2∶3,上底宽是
3 m,路基高是4 m,则路基的下底宽是( )
A.7 m B.9 m
C.12 m D.15 m
D
1.在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切(tangent),记作:tan A
即tan A=
∠A的对边
∠A的邻边
B
A
C
∠A的对边
∠A的邻边
2.tan A的值越大,梯子越陡.对于山坡来说,正切对应的是坡度
1.tanA是在直角三角形中定义的,∠A是一个锐角(注意数形结合,构造直角三角形).
2.tanA是一个完整的符号,表示∠A的正切,习惯省去“∠”号(注意tanA不表示tan乘以A).
3.tanA是一个比值(直角边之比,注意比的顺序,且tanA﹥0,无单位).
4.tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则正切值相等;两锐角的正切值相等,则这两个锐角相等.
正切
定义
坡度
∠A越大,tanA越大,梯子越陡
与梯子倾斜程度的关系
1.在Rt△ABC中, ∠C=90o ,AC=12,BC=5,那么tan A等于( )
2.如图,下面四个梯子最陡的是( )
A B C D
C.
B.
D.
A.
B
C
3.河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡比是1: (坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是( )
A.5 米 B.10米 C.15米 D.10 米
【解析】∵BC:AC=1: ,
A
B
C
BC=5米,
∴AC=
A
4.小明沿着坡度为1:2的山坡向上走了1 000 m,则他升高了( )
A. B.500 m
C. D.1 000 m
【解析】设升高了x m,由勾股定理得,x2+(2x)2=(1000)2,解得x=
A
5.如图,为了测量河两岸A,B两点的距离,在与AB垂直的方向点C处测得AC=a,∠ACB=α,那么AB等于( )
A.a·sinα B.a·tanα
C.a·cosα D.
【解析】在Rt△ABC中,tanα=
所以AB= a·tanα
B
6. 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D,则tan∠BCD= .
7. 如图,在Rt△ABC中,AC=2,BC=1,则tan A= .
8.把△ABC三边的长度都扩大为原来的2倍,则锐角A的正切值( )
A.缩小为原来的 B.不变
C.扩大为原来的2倍 D.扩大为原来的4倍
B
【规律方法】当直角三角形的锐角确定后,它的对边与邻边的比值也随之确定;比值与三角形的大小无关,只与倾斜角的大小有关.
9.如图,△ABC的顶点都在正方形网格的格点上,则tanC的值为( )
A
【解析】设小正方形的边长为1.取AB与格点的交点为D,AC与格点的交点为E,则
10.如图, 位于6×6的方格纸中,
则 = .
A
B
C
=
A
B
C
D
E
11.如图,在一次数学课外实践活动中,要求测教学楼的高度AB.小刚在D处用高1.5 m的测角仪CD,测得教学楼顶端A的仰角为30°,然后向教学楼前进40 m到达E,又测得教学楼顶端A的仰角为60°.求这幢教学楼的高度AB.
【解析】在Rt△AFG中,
∴
∴
∴
答:这幢教学楼的高度AB为
m.
在Rt△ACG中,
