鲁教版(五四制)数学七年级下册 10.4 线段的垂直平分线教案
文档属性
| 名称 | 鲁教版(五四制)数学七年级下册 10.4 线段的垂直平分线教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 43.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-19 17:56:06 | ||
图片预览



文档简介
线段的垂直平分线
【课时安排】
2课时
【第一课时】
【教学目标】
1.经历探索、猜测、证明的过程,进一步发展学生的推理证明意识和能力。
2.能够证明线段垂直平分线的性质定理、判定定理及其相关结论。
【教学重难点】
重点:线段的垂直平分线性质与逆定理及其的应用。
难点:线段的垂直平分线的逆定理的理解和证明。
【教学方法】
观察实践法,分组讨论法,讲练结合法,自主探究法。
教学手段:多媒体。
【教学过程】
一、从学生原有的认知结构提出问题。
这节课,我们来研究线段的垂直平分线的尺规作图和性质。
师生共同研究形成概念。
(一)线段垂直平分线的性质。
1.猜想:我们看看上面我们所作的线段的垂直平分线有什么性质?
引导学生自主发现线段垂直平分线的性质。
2.想一想书本上面:
应先让学生自己思考证明的思路和方法,并尝试写出证明过程。
线段垂直平分线上的点到这条线段两个端点的距离相等。
要证明一个图形上每一点都具有某种性质,只需要在图形上任取一点作代表。这一思想方法应让学生理解。
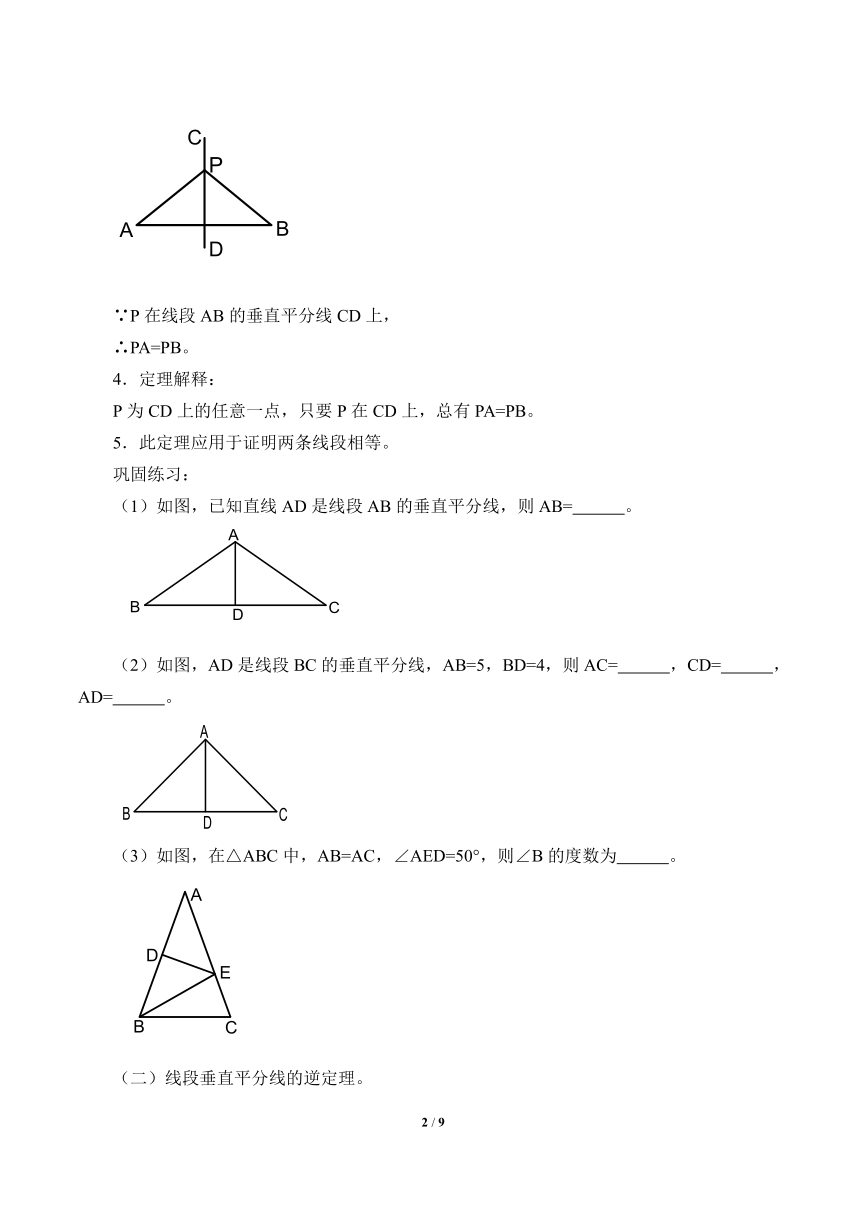
3.符号语言:
∵P在线段AB的垂直平分线CD上,
∴PA=PB。
4.定理解释:
P为CD上的任意一点,只要P在CD上,总有PA=PB。
5.此定理应用于证明两条线段相等。
巩固练习:
(1)如图,已知直线AD是线段AB的垂直平分线,则AB= 。
(2)如图,AD是线段BC的垂直平分线,AB=5,BD=4,则AC= ,CD= ,AD= 。
(3)如图,在△ABC中,AB=AC,∠AED=50°,则∠B的度数为 。
(二)线段垂直平分线的逆定理。
1.想一想书本。
因为这个命题不是“如果……那么……”的形式,所以学生说出或写出它的逆命题时可能会有一定的困难,帮助学生分析它的条件和结论,再写出其逆命题,最后应要求学生按证明的格式将证明过程书写出来。
猜想:我们说“线段垂直平分线上的点到这条线段两个端点的距离相等”,那么,到一条线段两个端点距离相等的点,在这条线段的垂直平分线上有什么性质?
引导学生自主发现线段垂直平分线的判定。
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
2.符号语言。
∵PA=PB,
∴P在线段AB的垂直平分线上。
3.定理解释。
只要有PA=PB,则P为CD上的任意一点。
4.此定理应用于证明一点在某条线段的垂直平分线上。
巩固练习:
(1)已知点A和线段BC,且AB=AC,则点A在 。
(2)如果平面内的点C、D、E到线段AB的两端点的距离相等,则C、D、E均在线段AB的 。
(3)设是线段AB的垂直平分线,且CA=CB,则点C一定 。
(三)讲解例题。
例题:
已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC。
求证:直线AO垂直平分线段BC。
证明:
∵AB=AC,
∴点A在线段BC的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上)。
同理,点O在线段BC的垂直平分线上。
∴直线AO是线段BC的垂直平分线(两点确定一条直线)。
(四)尺规做线段的垂直平分线。
已知:线段AB(如图)。
求作:线段AB的垂直平分线。
作法:
1.分别以点A和B为圆心,以大于AB的长为半径作弧,两弧相交于点C和D。
2.作直线CD。
直线CD就是线段AB的垂直平分线。
(五)随堂练习。
1.书本随堂练习。
2.如图,已知AB=AC=14cm,AB的垂直平分线交AC于D。
(1)若△DBC的周长为24cm,则BC= cm;
(2)若BC=8cm,则△BCD的周长是 cm。
(3)在△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,求AB、BC。
3.如图,在△ABC中,AB的垂直平分线交AC于D,如果AC=5cm,BC=4cm,AE=2cm,求△CDB的周长。
三、小结。
线段的垂直平分线在计算、证明、作图中都有着重要作用。在前面学习中,有一些用三角形全等的知识来解决问题,现在可用线段垂直平分线的定理及其逆定理来求解会更方便些。
【第二课时】
教学内容 线段的垂直平分线(二)
教学目标 1.能够利用直尺和圆规作已知线段的垂直平分线;已知底边及底边上的高,能够利用直尺和圆规做出等腰三角形。知道为什么这样做图,提高熟练地使用直尺和圆规作图的技能。 2.通过探索、猜测、证明的过程,进一步拓展学生的推理证明意识和能力。
教学重点 作已知线段的垂直平分线。
教学难点 理解三线共点的证明方法。
教学过程
教师活动 学生活动
一、线段垂直平分线的性质定理。 (一)让学生拿出教学准备好的纸片三角形,先折一条边作示范,然后让学生用折叠的方法找出每条边的垂直平分线。 (二)让学生观察:刚刚折出来的三条垂直平分线有什么关系?让学生自己经历探究的过程,不要直接给出答案或很有指向性的提示。 (三)让学生暂且把折纸放在一边,拿出圆规和直尺,画:—个任意的三角形,并利用所学知识做出三角形三条边的垂直平分线。要注意提醒个别学生作图的方法和步骤,强调作图的要求,培养学生的作图技能。 (四)让学生观察他们自己做出来的三条垂直平分线有什么性质,然后对照纸折的三条垂直平分线,看这个性质是不是它们共有的?换句话说,不管是什么样的三角形,它们的垂直平分线有没有什么共性?有的话,这个共性是什么?让学生提出猜想。 (五)让已经得出猜想的学生说出他们的猜想,并说明他们是怎么得到这个猜想的。在这时要注意表扬回答问题的学生,肯定他的发现,向学生强调:准确的图形由于直观地揭示了数学对象阶性质,因此有利于发现数学结论,而不准确的图形不利于发现数学结论,以此要求学生认真画图,养成好的习惯。 (六)肯定学生的发现;板书规范的表达;提问:对于这个猜想,你能用学过的知识来证明它吗?进一步渗透理性思考的意识,强调:只有经过证明的猜想才能确定其是否正确。 (七)启发学生思考:大家都知道两条直线交于一点,要证明三条直线相交于一点,是不是只要证明第三条直线也通过这两条直线的交点即可?也就是说,只要能证明其中两条直线的交点在另一条直线上即可。对这个证明。 (八)巡视之后,让基本可以证明的学生口述其证明思路,其他同学看他的证明是否正确、严谨。 (九)点评学生的回答,肯定其正确性,修正不规范的地方。让两位学生到黑板上画出图形,写出已知,求证并证明,其他学生在练习本上证明。让学生把思考落实到笔上。 (十)参照黑板上两位学生的证明,带学生把证明的思路再整理一遍,同时阐释三线共点的证明方法。,加深学生的认识,为以后的学习和使用打下基础。 二、两个作图的问题。 (一)让学生分组讨论:已知三角形的一条边及这条边上的高,你能作出三角形吗?如果能,能作几个?所作出的三角形都全等吗?让学生在讨论的过程中,思考并发表自己的见解,让学生体验合作学习,培养学生用数学地思考和表达的能力。分组时考虑到学生的搭配。 (二)让每组派一位代表说出小组的讨论结果,如果已经作出了图的话,用投影仪展示给全班同学看,让学生评判哪组的结果不但正确,而且漂亮。以此调动学生地积极性,体现学生的主体地位,向学生渗透追求数学结果正确、简洁、和谐的美的意识。 (三)赞赏地肯定所有同学的表现,表扬大家公认的作的好的组,让大家向他们学习,同时抓住其他小组的优点予以鼓励,保护他们对数学学习的热情。 (四)综合学生的讨论结果,给出问题的解答。同时,引导学生思考、讨论另外几个问题:已知等腰三角形的底边及底边上的高,你能用直尺和圆规作出等腰三角形吗?能作几个?它们之间有什么关系? (五)让学生动手画出符合要求的三角形,训练他们的作图技能,要注意提醒学生正确使用直尺和圆规,规范作图。 (六)要求学生自己写出作法,同时能说明理由。 三、已知底边及底边上的高,求作等腰三角形。 (一)用投影仪出示题目:已知底边及底边上的高,求作等腰三角形。进一步训练学生的作图技能。应注意要求学生根据题意写出已知和求作、规范作图并能说明理由。 (二)简单讲评,总结本节内容,作业布置。 1.在老师示范之后,大多数学生都顺利地折出三角形三条边的垂直平分线。 2.仔细观察三角形的三条垂直平分线,思考它们之间的关系。在探索过程中,可能从边的角度、也可能从角的角度猜想三条直线的关系,有的也注意到了三线共点的特点。 3.拿出圆规和直尺,作一个任意的三角形,比较熟练地做出三角形三条边的垂直平分线。在作图的同时熟悉作已知线段垂直平分线的作法,作图技能得到锻炼,加深对作已知线段垂直平分线的作法的理解。 4.认真观察自己所作的三条垂直平分线,图作的准确的学生比较容易观察到三条线交于一点,再结合折的三条垂直平分线,又有类似的性质,因此提出猜想:三线交于一点。但图画得不太难确的学生,难以观察到这个结果。 5.听发言的同学的猜想和如何发现结论的过程,受到很大的启发。同时,也感受到一个准确的图形对于揭示数学对象的性质、发现数学结论有很大的帮助,在老师的要求下,对作图的必要性有了更深刻的认识。 6.听讲,记下三角形三条边的垂直平分线的性质定理,思考如何对三线共点的猜想进行证明。但因为是初次接触这样抽象的证明,不知从哪里开始证明。 7.受到老师的启发,一边画草图一边思考这样证明是否正确。在验证思路准确无误之后,思考怎么证明。联想到上节课线段垂直平分线性质定理及其逆定理的同学,可以找到思路方法要逐步引导,不可操之过急。 8.听同学口述证明的思路,并判断其是否正确,不能证明的学生受到启发,也许也可以给出证明。 9.两位同学到黑板上证明,其他同学在练习本上写出已知求证和证明。因为已经经过了分析,绝大多数同学可以顺利地写出来。 10.在老师讲解的同时规范自己的证明,对三线共点的证明方法有了比较好的理解和认识。
板书设计 1.线段垂直平分线的性质定理。 2.两个作图的问题。 3.已知底边及底边上的高,求作等腰三角形。
教学反思 1.题目为进行作图的探索提供了空间,对于这个有挑战性的题目,学生很积极地思考、动手试验、展开讨论。讨论过程中,可能会有不同的意见,在商讨中加深对问题的理解。 2.非常积极地参与到评判讨论成果的活动中,对作为裁判者感到自豪,在观看其他组的成果时,既可以看到自己的不足,又加深了对问题的认识。由于老师对结论表达形式的要求,对于数学美有了一点感性的认识和体验,有了一点追求数学美的意识。 3.受到表扬和鼓励后,有更大的积极性投入到数学学习中。 4.因为这是刚才所讨论的问题的一个特例,所以可以比较容易得到解答:可以作出两个等腰三角形,它们分别位于底边的两侧,是全等的等腰三角形。 5.动手画出这两个三角形,比较熟练地使用直尺和圆规。 6.写出作法,说出理由。
课堂小结 1.经过刚才的探究和作图,很快地完成任务。经过训练,对于作图有了很好的掌握。 2.听讲,总结本节内容,记下作业。
9 / 9
【课时安排】
2课时
【第一课时】
【教学目标】
1.经历探索、猜测、证明的过程,进一步发展学生的推理证明意识和能力。
2.能够证明线段垂直平分线的性质定理、判定定理及其相关结论。
【教学重难点】
重点:线段的垂直平分线性质与逆定理及其的应用。
难点:线段的垂直平分线的逆定理的理解和证明。
【教学方法】
观察实践法,分组讨论法,讲练结合法,自主探究法。
教学手段:多媒体。
【教学过程】
一、从学生原有的认知结构提出问题。
这节课,我们来研究线段的垂直平分线的尺规作图和性质。
师生共同研究形成概念。
(一)线段垂直平分线的性质。
1.猜想:我们看看上面我们所作的线段的垂直平分线有什么性质?
引导学生自主发现线段垂直平分线的性质。
2.想一想书本上面:
应先让学生自己思考证明的思路和方法,并尝试写出证明过程。
线段垂直平分线上的点到这条线段两个端点的距离相等。
要证明一个图形上每一点都具有某种性质,只需要在图形上任取一点作代表。这一思想方法应让学生理解。
3.符号语言:
∵P在线段AB的垂直平分线CD上,
∴PA=PB。
4.定理解释:
P为CD上的任意一点,只要P在CD上,总有PA=PB。
5.此定理应用于证明两条线段相等。
巩固练习:
(1)如图,已知直线AD是线段AB的垂直平分线,则AB= 。
(2)如图,AD是线段BC的垂直平分线,AB=5,BD=4,则AC= ,CD= ,AD= 。
(3)如图,在△ABC中,AB=AC,∠AED=50°,则∠B的度数为 。
(二)线段垂直平分线的逆定理。
1.想一想书本。
因为这个命题不是“如果……那么……”的形式,所以学生说出或写出它的逆命题时可能会有一定的困难,帮助学生分析它的条件和结论,再写出其逆命题,最后应要求学生按证明的格式将证明过程书写出来。
猜想:我们说“线段垂直平分线上的点到这条线段两个端点的距离相等”,那么,到一条线段两个端点距离相等的点,在这条线段的垂直平分线上有什么性质?
引导学生自主发现线段垂直平分线的判定。
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
2.符号语言。
∵PA=PB,
∴P在线段AB的垂直平分线上。
3.定理解释。
只要有PA=PB,则P为CD上的任意一点。
4.此定理应用于证明一点在某条线段的垂直平分线上。
巩固练习:
(1)已知点A和线段BC,且AB=AC,则点A在 。
(2)如果平面内的点C、D、E到线段AB的两端点的距离相等,则C、D、E均在线段AB的 。
(3)设是线段AB的垂直平分线,且CA=CB,则点C一定 。
(三)讲解例题。
例题:
已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC。
求证:直线AO垂直平分线段BC。
证明:
∵AB=AC,
∴点A在线段BC的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上)。
同理,点O在线段BC的垂直平分线上。
∴直线AO是线段BC的垂直平分线(两点确定一条直线)。
(四)尺规做线段的垂直平分线。
已知:线段AB(如图)。
求作:线段AB的垂直平分线。
作法:
1.分别以点A和B为圆心,以大于AB的长为半径作弧,两弧相交于点C和D。
2.作直线CD。
直线CD就是线段AB的垂直平分线。
(五)随堂练习。
1.书本随堂练习。
2.如图,已知AB=AC=14cm,AB的垂直平分线交AC于D。
(1)若△DBC的周长为24cm,则BC= cm;
(2)若BC=8cm,则△BCD的周长是 cm。
(3)在△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,求AB、BC。
3.如图,在△ABC中,AB的垂直平分线交AC于D,如果AC=5cm,BC=4cm,AE=2cm,求△CDB的周长。
三、小结。
线段的垂直平分线在计算、证明、作图中都有着重要作用。在前面学习中,有一些用三角形全等的知识来解决问题,现在可用线段垂直平分线的定理及其逆定理来求解会更方便些。
【第二课时】
教学内容 线段的垂直平分线(二)
教学目标 1.能够利用直尺和圆规作已知线段的垂直平分线;已知底边及底边上的高,能够利用直尺和圆规做出等腰三角形。知道为什么这样做图,提高熟练地使用直尺和圆规作图的技能。 2.通过探索、猜测、证明的过程,进一步拓展学生的推理证明意识和能力。
教学重点 作已知线段的垂直平分线。
教学难点 理解三线共点的证明方法。
教学过程
教师活动 学生活动
一、线段垂直平分线的性质定理。 (一)让学生拿出教学准备好的纸片三角形,先折一条边作示范,然后让学生用折叠的方法找出每条边的垂直平分线。 (二)让学生观察:刚刚折出来的三条垂直平分线有什么关系?让学生自己经历探究的过程,不要直接给出答案或很有指向性的提示。 (三)让学生暂且把折纸放在一边,拿出圆规和直尺,画:—个任意的三角形,并利用所学知识做出三角形三条边的垂直平分线。要注意提醒个别学生作图的方法和步骤,强调作图的要求,培养学生的作图技能。 (四)让学生观察他们自己做出来的三条垂直平分线有什么性质,然后对照纸折的三条垂直平分线,看这个性质是不是它们共有的?换句话说,不管是什么样的三角形,它们的垂直平分线有没有什么共性?有的话,这个共性是什么?让学生提出猜想。 (五)让已经得出猜想的学生说出他们的猜想,并说明他们是怎么得到这个猜想的。在这时要注意表扬回答问题的学生,肯定他的发现,向学生强调:准确的图形由于直观地揭示了数学对象阶性质,因此有利于发现数学结论,而不准确的图形不利于发现数学结论,以此要求学生认真画图,养成好的习惯。 (六)肯定学生的发现;板书规范的表达;提问:对于这个猜想,你能用学过的知识来证明它吗?进一步渗透理性思考的意识,强调:只有经过证明的猜想才能确定其是否正确。 (七)启发学生思考:大家都知道两条直线交于一点,要证明三条直线相交于一点,是不是只要证明第三条直线也通过这两条直线的交点即可?也就是说,只要能证明其中两条直线的交点在另一条直线上即可。对这个证明。 (八)巡视之后,让基本可以证明的学生口述其证明思路,其他同学看他的证明是否正确、严谨。 (九)点评学生的回答,肯定其正确性,修正不规范的地方。让两位学生到黑板上画出图形,写出已知,求证并证明,其他学生在练习本上证明。让学生把思考落实到笔上。 (十)参照黑板上两位学生的证明,带学生把证明的思路再整理一遍,同时阐释三线共点的证明方法。,加深学生的认识,为以后的学习和使用打下基础。 二、两个作图的问题。 (一)让学生分组讨论:已知三角形的一条边及这条边上的高,你能作出三角形吗?如果能,能作几个?所作出的三角形都全等吗?让学生在讨论的过程中,思考并发表自己的见解,让学生体验合作学习,培养学生用数学地思考和表达的能力。分组时考虑到学生的搭配。 (二)让每组派一位代表说出小组的讨论结果,如果已经作出了图的话,用投影仪展示给全班同学看,让学生评判哪组的结果不但正确,而且漂亮。以此调动学生地积极性,体现学生的主体地位,向学生渗透追求数学结果正确、简洁、和谐的美的意识。 (三)赞赏地肯定所有同学的表现,表扬大家公认的作的好的组,让大家向他们学习,同时抓住其他小组的优点予以鼓励,保护他们对数学学习的热情。 (四)综合学生的讨论结果,给出问题的解答。同时,引导学生思考、讨论另外几个问题:已知等腰三角形的底边及底边上的高,你能用直尺和圆规作出等腰三角形吗?能作几个?它们之间有什么关系? (五)让学生动手画出符合要求的三角形,训练他们的作图技能,要注意提醒学生正确使用直尺和圆规,规范作图。 (六)要求学生自己写出作法,同时能说明理由。 三、已知底边及底边上的高,求作等腰三角形。 (一)用投影仪出示题目:已知底边及底边上的高,求作等腰三角形。进一步训练学生的作图技能。应注意要求学生根据题意写出已知和求作、规范作图并能说明理由。 (二)简单讲评,总结本节内容,作业布置。 1.在老师示范之后,大多数学生都顺利地折出三角形三条边的垂直平分线。 2.仔细观察三角形的三条垂直平分线,思考它们之间的关系。在探索过程中,可能从边的角度、也可能从角的角度猜想三条直线的关系,有的也注意到了三线共点的特点。 3.拿出圆规和直尺,作一个任意的三角形,比较熟练地做出三角形三条边的垂直平分线。在作图的同时熟悉作已知线段垂直平分线的作法,作图技能得到锻炼,加深对作已知线段垂直平分线的作法的理解。 4.认真观察自己所作的三条垂直平分线,图作的准确的学生比较容易观察到三条线交于一点,再结合折的三条垂直平分线,又有类似的性质,因此提出猜想:三线交于一点。但图画得不太难确的学生,难以观察到这个结果。 5.听发言的同学的猜想和如何发现结论的过程,受到很大的启发。同时,也感受到一个准确的图形对于揭示数学对象的性质、发现数学结论有很大的帮助,在老师的要求下,对作图的必要性有了更深刻的认识。 6.听讲,记下三角形三条边的垂直平分线的性质定理,思考如何对三线共点的猜想进行证明。但因为是初次接触这样抽象的证明,不知从哪里开始证明。 7.受到老师的启发,一边画草图一边思考这样证明是否正确。在验证思路准确无误之后,思考怎么证明。联想到上节课线段垂直平分线性质定理及其逆定理的同学,可以找到思路方法要逐步引导,不可操之过急。 8.听同学口述证明的思路,并判断其是否正确,不能证明的学生受到启发,也许也可以给出证明。 9.两位同学到黑板上证明,其他同学在练习本上写出已知求证和证明。因为已经经过了分析,绝大多数同学可以顺利地写出来。 10.在老师讲解的同时规范自己的证明,对三线共点的证明方法有了比较好的理解和认识。
板书设计 1.线段垂直平分线的性质定理。 2.两个作图的问题。 3.已知底边及底边上的高,求作等腰三角形。
教学反思 1.题目为进行作图的探索提供了空间,对于这个有挑战性的题目,学生很积极地思考、动手试验、展开讨论。讨论过程中,可能会有不同的意见,在商讨中加深对问题的理解。 2.非常积极地参与到评判讨论成果的活动中,对作为裁判者感到自豪,在观看其他组的成果时,既可以看到自己的不足,又加深了对问题的认识。由于老师对结论表达形式的要求,对于数学美有了一点感性的认识和体验,有了一点追求数学美的意识。 3.受到表扬和鼓励后,有更大的积极性投入到数学学习中。 4.因为这是刚才所讨论的问题的一个特例,所以可以比较容易得到解答:可以作出两个等腰三角形,它们分别位于底边的两侧,是全等的等腰三角形。 5.动手画出这两个三角形,比较熟练地使用直尺和圆规。 6.写出作法,说出理由。
课堂小结 1.经过刚才的探究和作图,很快地完成任务。经过训练,对于作图有了很好的掌握。 2.听讲,总结本节内容,记下作业。
9 / 9
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
