北师大版数学八年级下册 6.1 平行四边形的性质(1) 课件(共17张PPT)
文档属性
| 名称 | 北师大版数学八年级下册 6.1 平行四边形的性质(1) 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 589.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-19 21:37:12 | ||
图片预览




文档简介
(共17张PPT)
第6章 平行四边形
6.1 平行四边形的性质
第1课时 平行四边形的性质(1)
“哪里有数学,哪里就有美!”
——古希腊数学家普洛克拉斯
数学中的几何图形,在我们的生活中无处不在,它给这个五彩缤纷的世界增添了许多美感。
欣赏图片—引入新课
图中有你认识的几何图形吗?
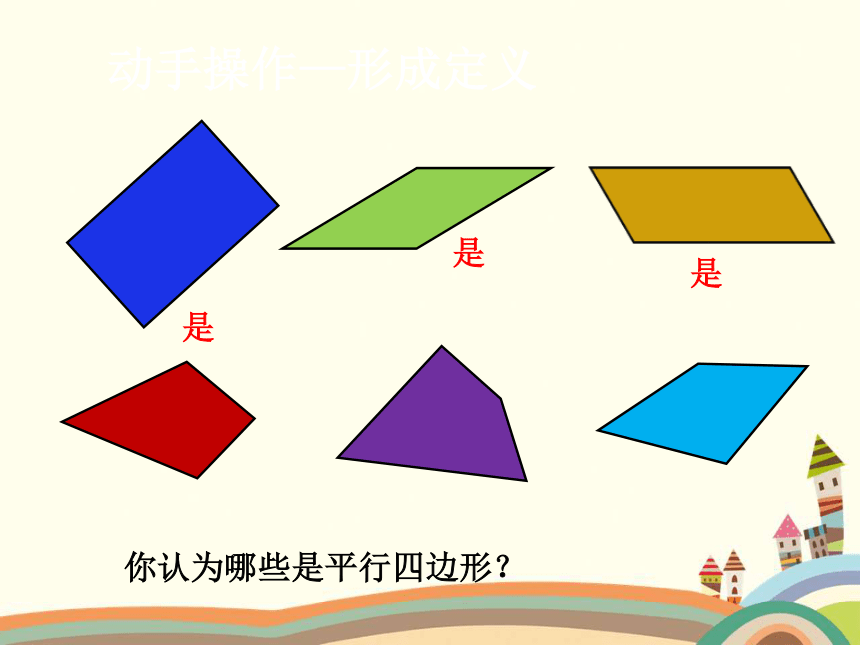
动手操作—形成定义
你认为哪些是平行四边形?
是
是
是
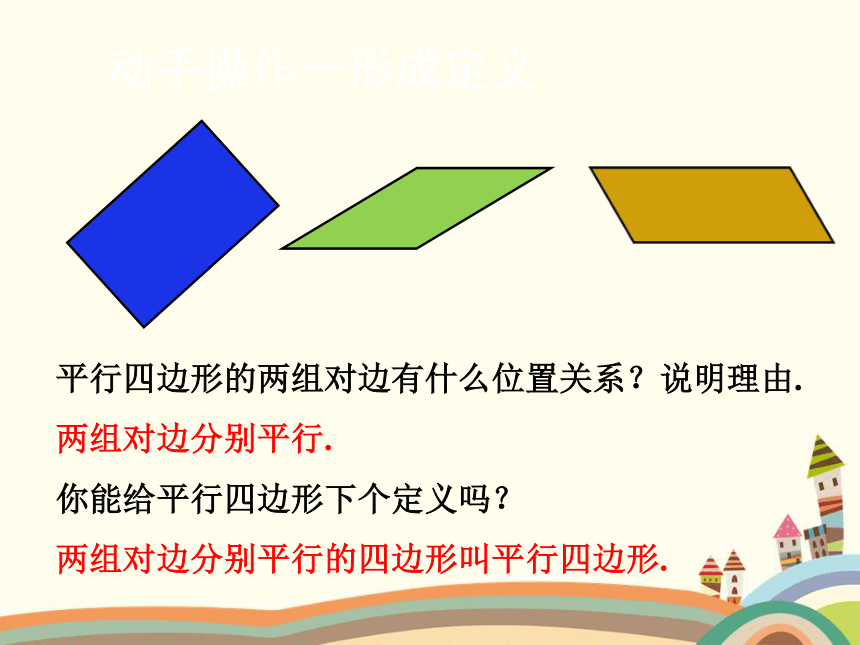
动手操作—形成定义
平行四边形的两组对边有什么位置关系?说明理由.
两组对边分别平行.
你能给平行四边形下个定义吗?
两组对边分别平行的四边形叫平行四边形.
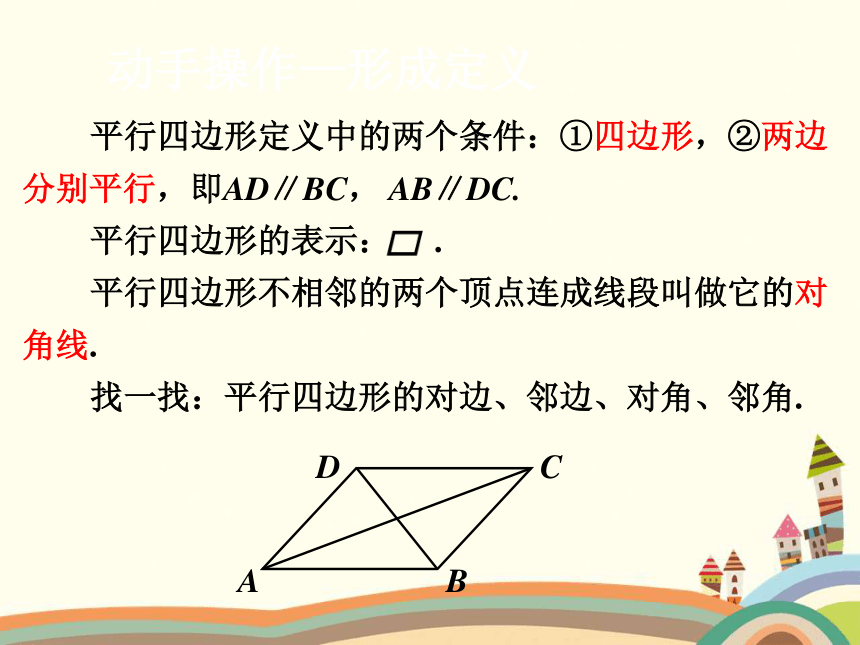
动手操作—形成定义
平行四边形定义中的两个条件:①四边形,②两边分别平行,即AD∥BC, AB∥DC.
平行四边形的表示: .
平行四边形不相邻的两个顶点连成线段叫做它的对角线.
找一找:平行四边形的对边、邻边、对角、邻角.
A
B
C
D
动手操作—形成定义
生活中常见到平行四边形的实例有哪些呢?你能举例说明吗?
动手操作—形成定义
想一想:(1)由平行四边形的定义你能直接知道它的对边具有什么位置关系吗?说说你的理由.
两组对边分别平行.
(2)用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?从拼图可以得到什么启示?
平行四边形可以由两个全等的三角形拼成,因此在解决平行四边形的问题时,通常可以连接对角线转化为两个全等的三角形进行解题.
实践探索—发现性质
小组活动:可采取度量、平移、旋转、折叠、拼图等方法探究平行四边形的对称性以及边、角的数量关系.
平行四边形是中心对称图形,不是轴对称图形,并且平行四边形两条对角线的交点是它的对称中心;平行四边形的邻角互补.
定理:平行四边形的对边相等.
定理:平行四边形的对角相等.
推理论证—验证性质
你能推导这两个定理吗?
提示:证明命题的一般步骤:
(1)结合命题,画出图形;
(2)根据图形结合命题的条件和结论写出已知和求证;
(3)找出由“已知”推导出“求证”的途径;
(4)写出证明过程.
定理:平行四边形的对边相等.
定理:平行四边形的对角相等.
推理论证—验证性质
已知:四边形ABCD是平行四边形.
求证: AB=CD, BC=DA, ∠B= ∠D,∠BAD= ∠DCB.
证明:连接AC,
∵四边形ABCD是平行四边形,
∴ AB∥CD, BC∥DA.
∴ ∠1= ∠2, ∠3= ∠4.
∵ AC = CA,
∴ △ABC≌ △CDA(ASA).
∴ AB=CD, BC=DA.
∴ ∠B= ∠D,∠BAD= ∠DCB.
B
C
D
A
1
3
2
4
应用巩固—运用性质
小试牛刀:
(1)在平行四边形ABCD 中,已知∠A= 130°,则∠B=_____ ,∠C=_____, ∠D= _____;
(2)平行四边形ABCD 中,∠A比∠B 大20°,则∠C=_____;
(3)在平行四边形ABCD 中,AD= 30, CD= 25,则AB=_____, BC=_____ .
50°
130°
50°
100°
25
30
应用巩固—运用性质
例1.已知:如图,在平行四边形ABCD 中,E,F是对角线AC上的两点,且AE=CF.
求证: BE=DF.
证明:∵四边形ABCD 是平行四边形,
∴ AB=CD,AB∥CD,
∴ ∠BAE= ∠DCF.
又∵ AE=CF,
∴△BAE≌△DCF.
∴ BE=DF.
B
C
D
A
E
F
应用巩固—运用性质
联系拓广:如图,在平行四边形ABCD 中, ∠ABC平分线交CD于点F,∠ADC的平分线交AB于点E.求证: BE=DF.
证明:∵四边形ABCD 是平行四边形,
∴ AD=BC,∠A= ∠C,
∴ ∠ADC= ∠ABC.
又∵ ∠ABC平分线交CD于点F,∠ADC平分线交AB于点E,
∴ ∠ADE= ∠CBF.
∴△ADE≌△CBF.∴ AE=CF.
又∵ AB=CD,
∴ AB-AE=CD-CF. ∴ BE=DF.
D
C
B
A
E
F
通过这节课的学习,你有哪些收获?还有什么疑惑?
评价反思—归纳小结
平行四边形
定义:两组对边分别平行的四边形叫做
平行四边形.
性质
边
角
对边相等
对边平行
对角相等
邻角互补
中心对称图形
数学思想:“化归”
教材习题6.1第1,2 题.
作业布置
谢谢大家!
再见!
第6章 平行四边形
6.1 平行四边形的性质
第1课时 平行四边形的性质(1)
“哪里有数学,哪里就有美!”
——古希腊数学家普洛克拉斯
数学中的几何图形,在我们的生活中无处不在,它给这个五彩缤纷的世界增添了许多美感。
欣赏图片—引入新课
图中有你认识的几何图形吗?
动手操作—形成定义
你认为哪些是平行四边形?
是
是
是
动手操作—形成定义
平行四边形的两组对边有什么位置关系?说明理由.
两组对边分别平行.
你能给平行四边形下个定义吗?
两组对边分别平行的四边形叫平行四边形.
动手操作—形成定义
平行四边形定义中的两个条件:①四边形,②两边分别平行,即AD∥BC, AB∥DC.
平行四边形的表示: .
平行四边形不相邻的两个顶点连成线段叫做它的对角线.
找一找:平行四边形的对边、邻边、对角、邻角.
A
B
C
D
动手操作—形成定义
生活中常见到平行四边形的实例有哪些呢?你能举例说明吗?
动手操作—形成定义
想一想:(1)由平行四边形的定义你能直接知道它的对边具有什么位置关系吗?说说你的理由.
两组对边分别平行.
(2)用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?从拼图可以得到什么启示?
平行四边形可以由两个全等的三角形拼成,因此在解决平行四边形的问题时,通常可以连接对角线转化为两个全等的三角形进行解题.
实践探索—发现性质
小组活动:可采取度量、平移、旋转、折叠、拼图等方法探究平行四边形的对称性以及边、角的数量关系.
平行四边形是中心对称图形,不是轴对称图形,并且平行四边形两条对角线的交点是它的对称中心;平行四边形的邻角互补.
定理:平行四边形的对边相等.
定理:平行四边形的对角相等.
推理论证—验证性质
你能推导这两个定理吗?
提示:证明命题的一般步骤:
(1)结合命题,画出图形;
(2)根据图形结合命题的条件和结论写出已知和求证;
(3)找出由“已知”推导出“求证”的途径;
(4)写出证明过程.
定理:平行四边形的对边相等.
定理:平行四边形的对角相等.
推理论证—验证性质
已知:四边形ABCD是平行四边形.
求证: AB=CD, BC=DA, ∠B= ∠D,∠BAD= ∠DCB.
证明:连接AC,
∵四边形ABCD是平行四边形,
∴ AB∥CD, BC∥DA.
∴ ∠1= ∠2, ∠3= ∠4.
∵ AC = CA,
∴ △ABC≌ △CDA(ASA).
∴ AB=CD, BC=DA.
∴ ∠B= ∠D,∠BAD= ∠DCB.
B
C
D
A
1
3
2
4
应用巩固—运用性质
小试牛刀:
(1)在平行四边形ABCD 中,已知∠A= 130°,则∠B=_____ ,∠C=_____, ∠D= _____;
(2)平行四边形ABCD 中,∠A比∠B 大20°,则∠C=_____;
(3)在平行四边形ABCD 中,AD= 30, CD= 25,则AB=_____, BC=_____ .
50°
130°
50°
100°
25
30
应用巩固—运用性质
例1.已知:如图,在平行四边形ABCD 中,E,F是对角线AC上的两点,且AE=CF.
求证: BE=DF.
证明:∵四边形ABCD 是平行四边形,
∴ AB=CD,AB∥CD,
∴ ∠BAE= ∠DCF.
又∵ AE=CF,
∴△BAE≌△DCF.
∴ BE=DF.
B
C
D
A
E
F
应用巩固—运用性质
联系拓广:如图,在平行四边形ABCD 中, ∠ABC平分线交CD于点F,∠ADC的平分线交AB于点E.求证: BE=DF.
证明:∵四边形ABCD 是平行四边形,
∴ AD=BC,∠A= ∠C,
∴ ∠ADC= ∠ABC.
又∵ ∠ABC平分线交CD于点F,∠ADC平分线交AB于点E,
∴ ∠ADE= ∠CBF.
∴△ADE≌△CBF.∴ AE=CF.
又∵ AB=CD,
∴ AB-AE=CD-CF. ∴ BE=DF.
D
C
B
A
E
F
通过这节课的学习,你有哪些收获?还有什么疑惑?
评价反思—归纳小结
平行四边形
定义:两组对边分别平行的四边形叫做
平行四边形.
性质
边
角
对边相等
对边平行
对角相等
邻角互补
中心对称图形
数学思想:“化归”
教材习题6.1第1,2 题.
作业布置
谢谢大家!
再见!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
