人教版数学八年级下册 18.1 平行四边形的性质(1) 课件(共19张PPT)
文档属性
| 名称 | 人教版数学八年级下册 18.1 平行四边形的性质(1) 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 734.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-19 21:39:21 | ||
图片预览




文档简介
(共33张PPT)
18.1 平行四边形
第18章 平行四边形
第1课时 平行四边形的性质(1)
18.1.1 平行四边形的性质
创设情境 导入新课
问题(1) 你们留意观察过阳光透过长方形窗口投在地面的影子是什么形状吗?
太阳光属于平行光,窗口在地面上的影子通常是平行四边形.
问题(2) 爱动脑筋的小刚观察到平行四边形影子有一种对称美,他说只要量出一个内角的度数,就能知道其余三个内角的度数;只需测出一组相邻的边长,便能计算出它的周长,这是为什么呢?
创设情境 导入新课
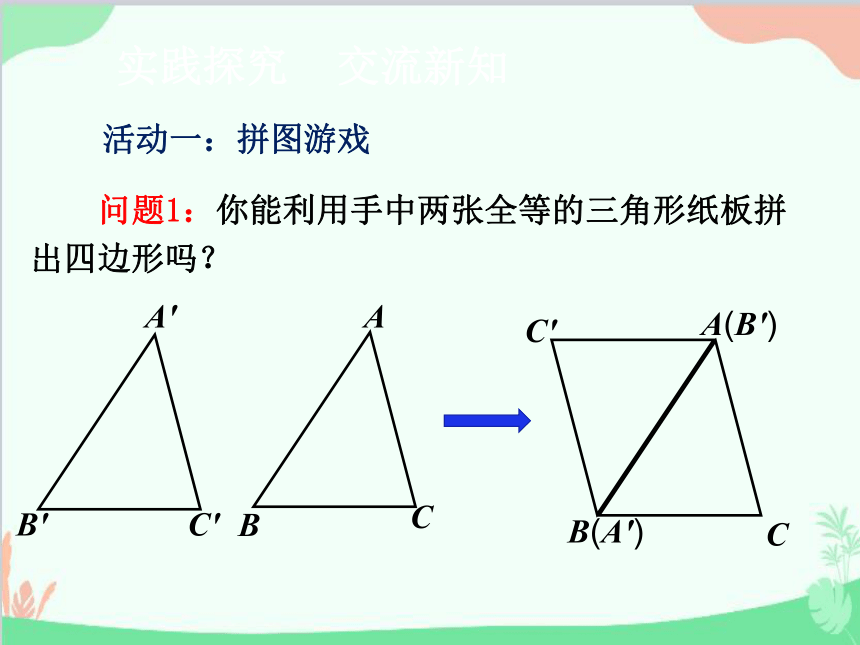
问题1:你能利用手中两张全等的三角形纸板拼出四边形吗?
A'
B'
C'
A
B
C
C'
A(B')
B(A')
C
实践探究 交流新知
活动一:拼图游戏
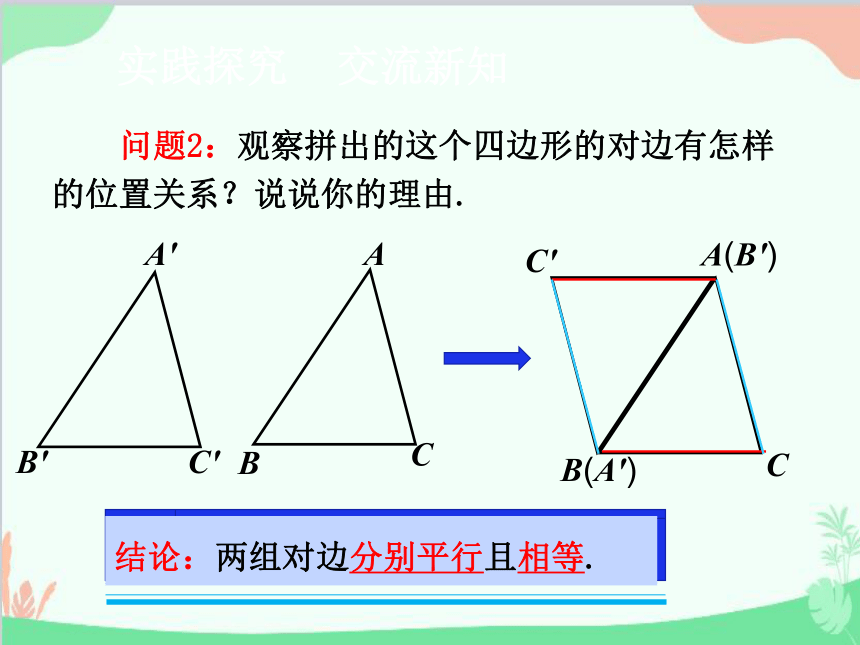
问题2:观察拼出的这个四边形的对边有怎样的位置关系?说说你的理由.
结论:两组对边分别平行且相等.
实践探究 交流新知
A'
B'
C'
A
B
C
C'
A(B')
B(A')
C
结论:两组对边分别平行的四边形是平行四边形.
实践探究 交流新知
实践探究 交流新知
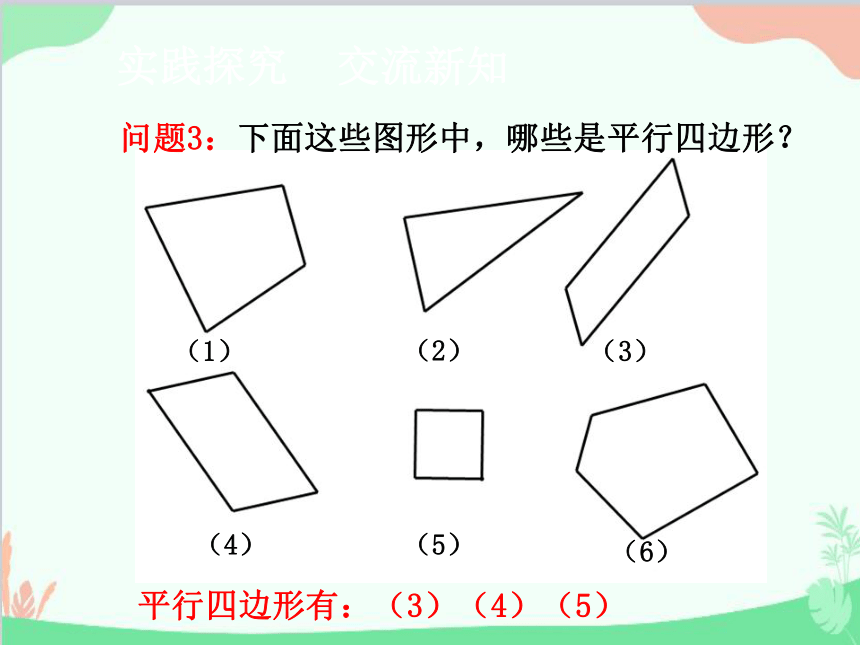
问题3:下面这些图形中,哪些是平行四边形?
平行四边形有:(3)(4)(5)
(1)
(2)
(3)
(4)
(5)
(6)
实践探究 交流新知
问题4:根据定义画一个平行四边形.
A
D
B
C
如图,平行四边形 ,记作 ,
读作:平行四边形 .
平行四边形通常用“ ”表示,
实践探究 交流新知
如图,平行四边形ABCD中,AB和CD,AD和BC分别为对边;∠A和∠C,∠B和∠D分别为对角;
AC,BD为对角线.
活动要求:
(1)请你适当利用材料袋里的学具;
(2)可以采用度量、平移、旋转、折叠、拼图等方法;
(3)通过小组合作探究平行四边形有哪些性质;
(4)结论写在练习本上.
实践探究 交流新知
活动二:探究平行四边形的性质
利用以前学习的几何知识通过说理能验证你得到的结论吗?
连接平行四边形的对角线,是常作的辅助线,它构造出两个全等的三角形,从而将四边形问题转化为熟悉的三角形问题.充分体现了由未知转化为已知、由繁化简的数学思想.
实践探究 交流新知
活动总结:平行四边形的性质
(2)平行四边形的对角相等;
(3)平行四边形的邻角互补.
(1)平行四边形的对边相等;
实践探究 交流新知
A
E
B
D
F
C
例1 如图,在 中,DE⊥AB,BF⊥DC,垂足分别为E、F.求证:AE=CF.
≌
实践探究 交流新知
活动步骤及要求:
实践探究 交流新知
活动三:探究平行线间的距离
归纳:平行线间的距离处处相等.
实践探究 交流新知
经过测量你发现MM',NN',PP',QQ'……有何关系?
在直线AB上再取一点E,试一试,你能得出什么结论?
某时刻小刚用量角器量出地面上平行四边形影子的一个内角是60°,就说知道了其余三个内角的度数;又用直尺量出一组邻边的长度分别是40 cm和55 cm,便胸有成竹地说能够计算出这个平行四边形的周长.你知道小刚是如何计算的吗?这样计算的根据是什么?
开放训练 体现应用
其余三个内角度数分别为120゜、60゜、120゜;
根据:平行四边形对角相等、邻角互补.
平行四边形的周长为190 cm;
根据:平行四边形对边相等.
1.平行四边形的定义:两组对边分别平行的四边形是平行四边形;
收获与感悟:
2.平行四边形的性质:平行四边形对边相等、对角相等、邻角互补;
3.平行线间的距离处处相等.
反思小结 持续发展
如图,已知任意三点A,B,C,是否存在点D,使A,B,C,D围成一个平行四边形?如果存在,请你作出这个平行四边形;如果不存在,请说明理由.
作业布置
A
B
C
18.1 平行四边形
第18章 平行四边形
第1课时 平行四边形的性质(1)
18.1.1 平行四边形的性质
创设情境 导入新课
问题(1) 你们留意观察过阳光透过长方形窗口投在地面的影子是什么形状吗?
太阳光属于平行光,窗口在地面上的影子通常是平行四边形.
问题(2) 爱动脑筋的小刚观察到平行四边形影子有一种对称美,他说只要量出一个内角的度数,就能知道其余三个内角的度数;只需测出一组相邻的边长,便能计算出它的周长,这是为什么呢?
创设情境 导入新课
问题1:你能利用手中两张全等的三角形纸板拼出四边形吗?
A'
B'
C'
A
B
C
C'
A(B')
B(A')
C
实践探究 交流新知
活动一:拼图游戏
问题2:观察拼出的这个四边形的对边有怎样的位置关系?说说你的理由.
结论:两组对边分别平行且相等.
实践探究 交流新知
A'
B'
C'
A
B
C
C'
A(B')
B(A')
C
结论:两组对边分别平行的四边形是平行四边形.
实践探究 交流新知
实践探究 交流新知
问题3:下面这些图形中,哪些是平行四边形?
平行四边形有:(3)(4)(5)
(1)
(2)
(3)
(4)
(5)
(6)
实践探究 交流新知
问题4:根据定义画一个平行四边形.
A
D
B
C
如图,平行四边形 ,记作 ,
读作:平行四边形 .
平行四边形通常用“ ”表示,
实践探究 交流新知
如图,平行四边形ABCD中,AB和CD,AD和BC分别为对边;∠A和∠C,∠B和∠D分别为对角;
AC,BD为对角线.
活动要求:
(1)请你适当利用材料袋里的学具;
(2)可以采用度量、平移、旋转、折叠、拼图等方法;
(3)通过小组合作探究平行四边形有哪些性质;
(4)结论写在练习本上.
实践探究 交流新知
活动二:探究平行四边形的性质
利用以前学习的几何知识通过说理能验证你得到的结论吗?
连接平行四边形的对角线,是常作的辅助线,它构造出两个全等的三角形,从而将四边形问题转化为熟悉的三角形问题.充分体现了由未知转化为已知、由繁化简的数学思想.
实践探究 交流新知
活动总结:平行四边形的性质
(2)平行四边形的对角相等;
(3)平行四边形的邻角互补.
(1)平行四边形的对边相等;
实践探究 交流新知
A
E
B
D
F
C
例1 如图,在 中,DE⊥AB,BF⊥DC,垂足分别为E、F.求证:AE=CF.
≌
实践探究 交流新知
活动步骤及要求:
实践探究 交流新知
活动三:探究平行线间的距离
归纳:平行线间的距离处处相等.
实践探究 交流新知
经过测量你发现MM',NN',PP',QQ'……有何关系?
在直线AB上再取一点E,试一试,你能得出什么结论?
某时刻小刚用量角器量出地面上平行四边形影子的一个内角是60°,就说知道了其余三个内角的度数;又用直尺量出一组邻边的长度分别是40 cm和55 cm,便胸有成竹地说能够计算出这个平行四边形的周长.你知道小刚是如何计算的吗?这样计算的根据是什么?
开放训练 体现应用
其余三个内角度数分别为120゜、60゜、120゜;
根据:平行四边形对角相等、邻角互补.
平行四边形的周长为190 cm;
根据:平行四边形对边相等.
1.平行四边形的定义:两组对边分别平行的四边形是平行四边形;
收获与感悟:
2.平行四边形的性质:平行四边形对边相等、对角相等、邻角互补;
3.平行线间的距离处处相等.
反思小结 持续发展
如图,已知任意三点A,B,C,是否存在点D,使A,B,C,D围成一个平行四边形?如果存在,请你作出这个平行四边形;如果不存在,请说明理由.
作业布置
A
B
C
