24.2.1 点和圆的位置关系(2)课件(共24张PPT)
文档属性
| 名称 | 24.2.1 点和圆的位置关系(2)课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 934.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-20 08:37:09 | ||
图片预览






文档简介
(共24张PPT)
人教版 九年级上册
24.2.1点和圆的位置关系(2)
过已知三点点 A、B、C画圆
复习旧知
A
B
C
已知三点共线
已知三点不共线
A
B
C
A
B
C
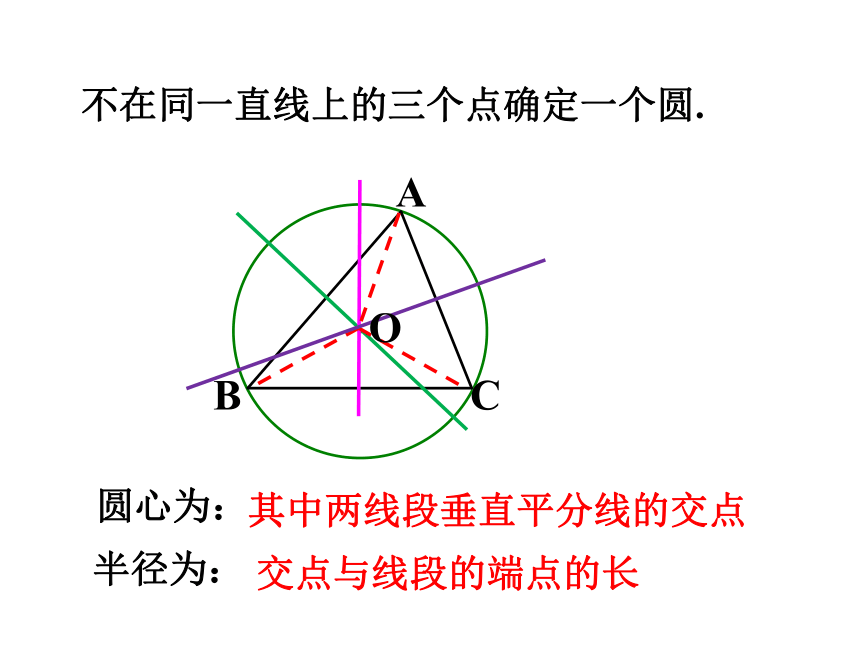
不在同一直线上的三个点确定一个圆.
O
圆心为:
半径为:
其中两线段垂直平分线的交点
交点与线段的端点的长
当三个点同一直线L上时,如图中的点A,B,C,要求作一个圆,使它经过A,B,C三点,可能吗?
L
A
B
C
探究新知
假设经过同一直线L上的三点A、B、C三点可以作一个圆,
OB=OC
∴点O到这三个点的距离相等,
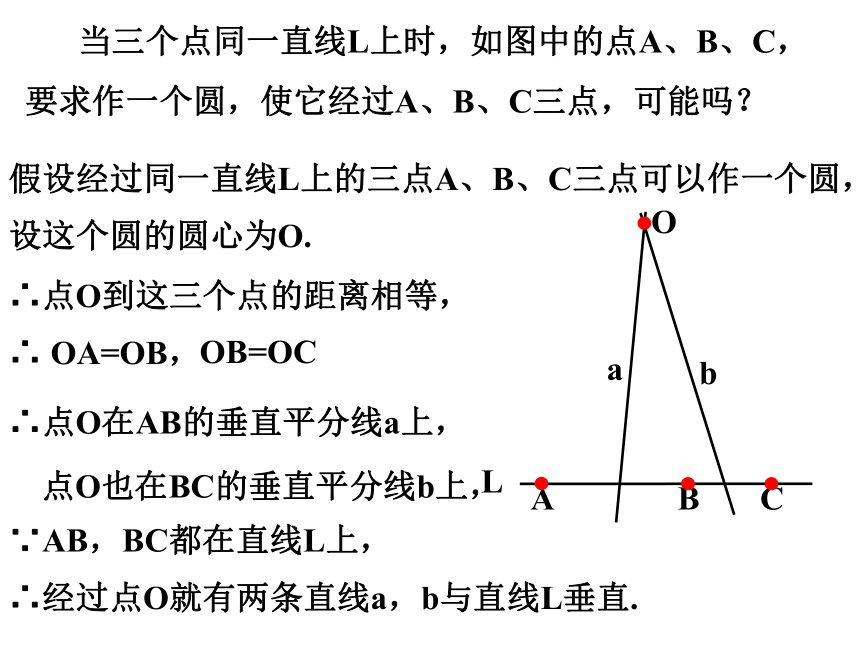
当三个点同一直线L上时,如图中的点A、B、C,要求作一个圆,使它经过A、B、C三点,可能吗?
L
A
B
C
设这个圆的圆心为O.
∴ OA=OB,
∴点O在AB的垂直平分线a上,
点O也在BC的垂直平分线b上,
∵AB,BC都在直线L上,
∴经过点O就有两条直线a,b与直线L垂直.
O
a
b
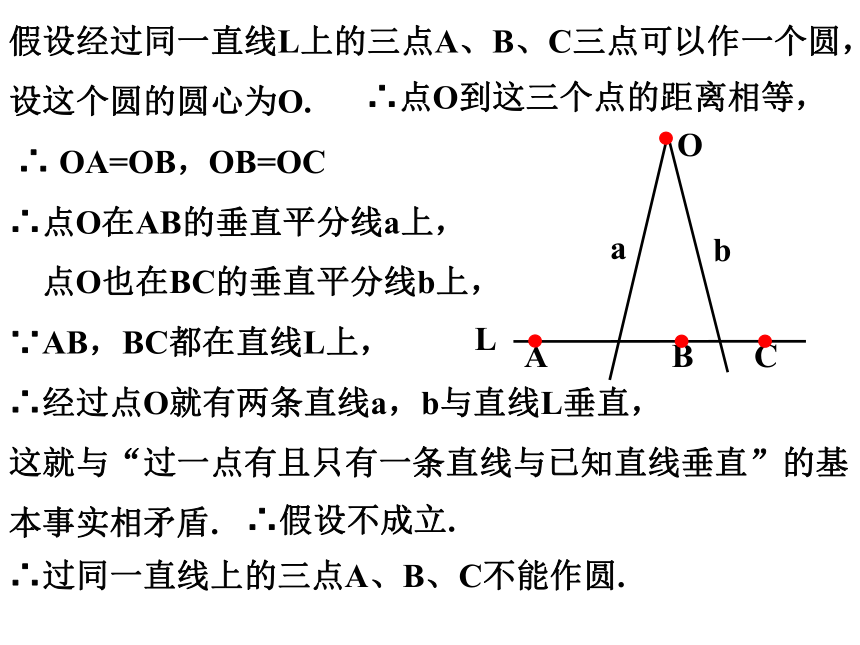
假设经过同一直线L上的三点A、B、C三点可以作一个圆,设这个圆的圆心为O.
∴ OA=OB,
∴点O在AB的垂直平分线a上,
点O也在BC的垂直平分线b上,
∵AB,BC都在直线L上,
∴经过点O就有两条直线a,b与直线L垂直,
这就与“过一点有且只有一条直线与已知直线垂直”的基本事实相矛盾.
OB=OC
∴假设不成立.
∴点O到这三个点的距离相等,
L
A
B
C
O
∴过同一直线上的三点A、B、C不能作圆.
a
b
反证法:证明不是直接从题设退出结论,而是先假设命题结论不成立,然后通过推理,得出矛盾的结果,最后断言结论一定成立.这样的证明方法叫做反证法.
这一命题成立时,运用了一种新的证明方法:反证法.
我们刚才用来证明命题:
过同一直线上的三点A、B、C不能作圆.
对于一些命题的证明,它独特,简便,实用.
“反证法”是初中数学学习中一种特殊的证明方法,
1.分清所证命题的条件和结论
运用“反证法”进行证明命题的关键:
2.熟记推理步骤
1.分清所证命题的条件和结论
运用“反证法”进行证明命题的关键:
2.熟记推理步骤
“过同一直线上的三点不能作圆”
如证明命题
条件是
结论是
“同一直线上的三点”
“不能使圆经过三点”
运用“反证法”进行证明命题的关键:
2.熟记推理步骤
第一步:
即假设命题的结论的反面为正确的.
反设.
第二步:
推理发现矛盾.
第三步:
推翻假设,证明原命题成立.
2.熟记推理步骤
第一步:
即假设命题的结论的反面为正确的.
反设.
如上述命题即
“假设能作圆经过同一直线上的三点”
∴过同一直线上的三点不能作圆.
第二步:
推理发现矛盾.
从反设出发,逐步推理,
发现与基本事实矛盾
第三步:
推翻假设,证明原命题成立.
已知,如图,直线AB∥CD,直线EF分别交AB,CD于点O1,O2.
假设∠EO1B≠∠EO2D
两条平行线被第三条直线所截,同位角相等.
A
B
C
E
F
D
O1
O2
求证:∠EO1B=∠EO2D.
学以致用
用反证法证明
第一步:
反设.
已知,如图,直线AB∥CD,直线EF分别交AB,CD于点O1,O2.
过点O1作直线A′B′,
假设∠EO1B≠∠EO2D,
使∠EO1B ′=∠EO2D,
∴ A′B′∥CD.
∵∠EO1B ′=∠EO2D,
定理
证明:
两条平行线被第三条直线所截,同位角相等.
A
B
C
E
F
D
O1
O2
A′
B′
求证:∠EO1B=∠EO2D.
∵ AB∥CD,
∴经过点O1就有两条直线AB,A′B′与直线CD平行,
已知,如图,直线AB∥CD,直线EF分别交AB,CD于点O1,O2. 求证:∠EO1B=∠EO2D
证明:
∴经过点O1就有两条直线AB,A′B′与直线CD平行,
这就与“过直线外一点有且只有一条直线与这条直线平行”的基本事实相矛盾.
过点O1作直线A′B′,
∴假设不成立.
假设∠EO1B≠∠EO2D,
使∠EO1B ′=∠EO2D,
∴ A′B′∥CD.
∵∠EO1B ′=∠EO2D,
∵ AB∥CD,
A
B
C
E
F
D
O1
O2
∴ ∠EO1B=∠EO2D.
运用“反证法”证明命题
一个三角形中不可能有两个角是直角.
假设一个三角形中有两个角是直角.
证明:
不妨设△ ABC中,
∠A=90°,∠B=90°,
∴ ∠A+∠B+∠C=
90°+90°+∠C
=180°+ ∠C
>180°
这就与“三角形内角和等于180”的基本事实相矛盾.
∴假设不成立.
∴一个三角形中不可能有两个角是直角.
1.用反证法证明命题“在△ABC中,若∠B≠ ∠C,
则AB≠AC”时,应先假设( ).
A. ∠B=∠C B.AB>AC
C. AB<AC D.AB ≠ AC
巩固新知
D
2.用反证法证明命题“如果a>b,那么a3>b3”
时,应先假设( ).
A. a3=b3 B.a3>b3
C. a=b或a<b D.a3=b3或a3<b3
D
3.用反证法证明时,假设结论“点在圆外”不成
立,那么点与圆的位置关系只能是( ).
A. 点在圆内 B.点在圆上
C. 点在圆心上 D.点在圆上或圆内
D
4.用反证法证明命题“在一个三角形中,不可能
有两个内角是钝角”时,第一步应先假设:
.
在一个三角形中,可以有两个内角是钝角
孔文举年十岁,随父到洛。时李元礼有盛名,为司隶校尉。诣门者,皆俊才清称及中表亲戚,乃通。文举至门,谓吏曰:“我是李府君亲。”既通,前坐。元礼问曰:“君与仆有何亲 ”对曰:“昔先君仲尼与君先人伯阳有师资之尊,是仆与君奕世为通好也。”元礼及宾客莫不奇之。太中大夫陈韪后至,人以其语语之,韪曰:“小时了了,大未必佳。”文举曰:“想君小时,必当了了。”韪大踧踖。
数学花絮
∵上帝全能,
∴让上帝造出一石头,
求证:不存在全能的上帝.
证明:
假设存在全能的上帝.
∵上帝举不动这块石头,
这就与假设“存在全能的上帝”相矛盾,
∴上帝不是全能的.
∴原来的假设是错的,
这块石头是上帝举不动的,
∴不存在全能的上帝.
今天作业
用反证法证明命题:圆的两条不是直径的
相交弦不能互相平分.
如图,已知,在⊙O中,不是直径的弦AB与CD相交于点P.
求证:AB与CD不能互相平分.
D
·
O
A
B
C
P
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 九年级上册
24.2.1点和圆的位置关系(2)
过已知三点点 A、B、C画圆
复习旧知
A
B
C
已知三点共线
已知三点不共线
A
B
C
A
B
C
不在同一直线上的三个点确定一个圆.
O
圆心为:
半径为:
其中两线段垂直平分线的交点
交点与线段的端点的长
当三个点同一直线L上时,如图中的点A,B,C,要求作一个圆,使它经过A,B,C三点,可能吗?
L
A
B
C
探究新知
假设经过同一直线L上的三点A、B、C三点可以作一个圆,
OB=OC
∴点O到这三个点的距离相等,
当三个点同一直线L上时,如图中的点A、B、C,要求作一个圆,使它经过A、B、C三点,可能吗?
L
A
B
C
设这个圆的圆心为O.
∴ OA=OB,
∴点O在AB的垂直平分线a上,
点O也在BC的垂直平分线b上,
∵AB,BC都在直线L上,
∴经过点O就有两条直线a,b与直线L垂直.
O
a
b
假设经过同一直线L上的三点A、B、C三点可以作一个圆,设这个圆的圆心为O.
∴ OA=OB,
∴点O在AB的垂直平分线a上,
点O也在BC的垂直平分线b上,
∵AB,BC都在直线L上,
∴经过点O就有两条直线a,b与直线L垂直,
这就与“过一点有且只有一条直线与已知直线垂直”的基本事实相矛盾.
OB=OC
∴假设不成立.
∴点O到这三个点的距离相等,
L
A
B
C
O
∴过同一直线上的三点A、B、C不能作圆.
a
b
反证法:证明不是直接从题设退出结论,而是先假设命题结论不成立,然后通过推理,得出矛盾的结果,最后断言结论一定成立.这样的证明方法叫做反证法.
这一命题成立时,运用了一种新的证明方法:反证法.
我们刚才用来证明命题:
过同一直线上的三点A、B、C不能作圆.
对于一些命题的证明,它独特,简便,实用.
“反证法”是初中数学学习中一种特殊的证明方法,
1.分清所证命题的条件和结论
运用“反证法”进行证明命题的关键:
2.熟记推理步骤
1.分清所证命题的条件和结论
运用“反证法”进行证明命题的关键:
2.熟记推理步骤
“过同一直线上的三点不能作圆”
如证明命题
条件是
结论是
“同一直线上的三点”
“不能使圆经过三点”
运用“反证法”进行证明命题的关键:
2.熟记推理步骤
第一步:
即假设命题的结论的反面为正确的.
反设.
第二步:
推理发现矛盾.
第三步:
推翻假设,证明原命题成立.
2.熟记推理步骤
第一步:
即假设命题的结论的反面为正确的.
反设.
如上述命题即
“假设能作圆经过同一直线上的三点”
∴过同一直线上的三点不能作圆.
第二步:
推理发现矛盾.
从反设出发,逐步推理,
发现与基本事实矛盾
第三步:
推翻假设,证明原命题成立.
已知,如图,直线AB∥CD,直线EF分别交AB,CD于点O1,O2.
假设∠EO1B≠∠EO2D
两条平行线被第三条直线所截,同位角相等.
A
B
C
E
F
D
O1
O2
求证:∠EO1B=∠EO2D.
学以致用
用反证法证明
第一步:
反设.
已知,如图,直线AB∥CD,直线EF分别交AB,CD于点O1,O2.
过点O1作直线A′B′,
假设∠EO1B≠∠EO2D,
使∠EO1B ′=∠EO2D,
∴ A′B′∥CD.
∵∠EO1B ′=∠EO2D,
定理
证明:
两条平行线被第三条直线所截,同位角相等.
A
B
C
E
F
D
O1
O2
A′
B′
求证:∠EO1B=∠EO2D.
∵ AB∥CD,
∴经过点O1就有两条直线AB,A′B′与直线CD平行,
已知,如图,直线AB∥CD,直线EF分别交AB,CD于点O1,O2. 求证:∠EO1B=∠EO2D
证明:
∴经过点O1就有两条直线AB,A′B′与直线CD平行,
这就与“过直线外一点有且只有一条直线与这条直线平行”的基本事实相矛盾.
过点O1作直线A′B′,
∴假设不成立.
假设∠EO1B≠∠EO2D,
使∠EO1B ′=∠EO2D,
∴ A′B′∥CD.
∵∠EO1B ′=∠EO2D,
∵ AB∥CD,
A
B
C
E
F
D
O1
O2
∴ ∠EO1B=∠EO2D.
运用“反证法”证明命题
一个三角形中不可能有两个角是直角.
假设一个三角形中有两个角是直角.
证明:
不妨设△ ABC中,
∠A=90°,∠B=90°,
∴ ∠A+∠B+∠C=
90°+90°+∠C
=180°+ ∠C
>180°
这就与“三角形内角和等于180”的基本事实相矛盾.
∴假设不成立.
∴一个三角形中不可能有两个角是直角.
1.用反证法证明命题“在△ABC中,若∠B≠ ∠C,
则AB≠AC”时,应先假设( ).
A. ∠B=∠C B.AB>AC
C. AB<AC D.AB ≠ AC
巩固新知
D
2.用反证法证明命题“如果a>b,那么a3>b3”
时,应先假设( ).
A. a3=b3 B.a3>b3
C. a=b或a<b D.a3=b3或a3<b3
D
3.用反证法证明时,假设结论“点在圆外”不成
立,那么点与圆的位置关系只能是( ).
A. 点在圆内 B.点在圆上
C. 点在圆心上 D.点在圆上或圆内
D
4.用反证法证明命题“在一个三角形中,不可能
有两个内角是钝角”时,第一步应先假设:
.
在一个三角形中,可以有两个内角是钝角
孔文举年十岁,随父到洛。时李元礼有盛名,为司隶校尉。诣门者,皆俊才清称及中表亲戚,乃通。文举至门,谓吏曰:“我是李府君亲。”既通,前坐。元礼问曰:“君与仆有何亲 ”对曰:“昔先君仲尼与君先人伯阳有师资之尊,是仆与君奕世为通好也。”元礼及宾客莫不奇之。太中大夫陈韪后至,人以其语语之,韪曰:“小时了了,大未必佳。”文举曰:“想君小时,必当了了。”韪大踧踖。
数学花絮
∵上帝全能,
∴让上帝造出一石头,
求证:不存在全能的上帝.
证明:
假设存在全能的上帝.
∵上帝举不动这块石头,
这就与假设“存在全能的上帝”相矛盾,
∴上帝不是全能的.
∴原来的假设是错的,
这块石头是上帝举不动的,
∴不存在全能的上帝.
今天作业
用反证法证明命题:圆的两条不是直径的
相交弦不能互相平分.
如图,已知,在⊙O中,不是直径的弦AB与CD相交于点P.
求证:AB与CD不能互相平分.
D
·
O
A
B
C
P
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
