24.2.2 直线和圆的位置关系(2)课件(共27张PPT)
文档属性
| 名称 | 24.2.2 直线和圆的位置关系(2)课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-20 00:00:00 | ||
图片预览





文档简介
(共27张PPT)
人教版 九年级上册
24.2.2直线和圆的位置关系(2)
直线和圆相切是直线和圆的位置关系中特殊并且重要的一种,圆的切线是连接直线型与曲线型的重要桥梁,是研究三角形内切圆、切线长定理和正多边形与圆的关系的基础.
切线的判定定理与性质定理揭示了直线和圆的半径的特殊位置关系,即,切线过半径外端并与这条半径垂直.两个定理互为逆命题.切线判定定理的探究过程体现了由一般到特殊的研究方法.
课件说明
学习目标: 1.理解切线的判定定理与性质定理; 2.会应用切线的判定定理和性质定理解决简单问题.
学习重点: 切线的判定定理和性质定理的应用.
课件说明
1.直线和圆有哪些位置关系?
2.如何判断直线和圆相切?
相切
相离
相交
①直线和圆有唯一的公共点;
②圆心到直线的距离和圆的半径相等.
复习旧知
如图,在⊙O中,经过半径 OA 的外端点 A 作直线L⊥OA,则圆心 O 到直线 L的距离是多少?直线 L和⊙O有什么位置关系?
经过半径的外端并且垂直于这条半径的直线是圆的切线.
L
O
A
等于半径OA
相切
学习新知
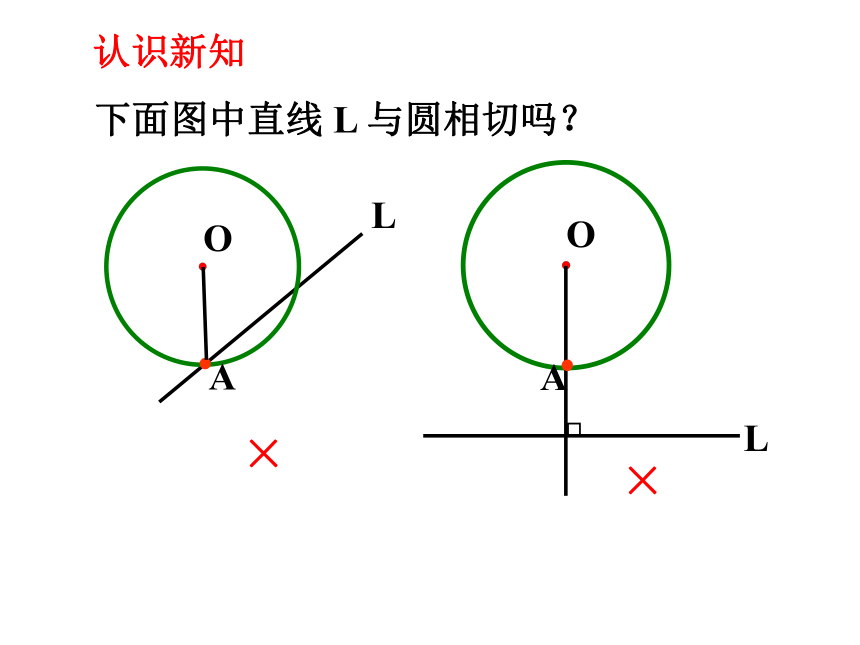
下面图中直线 L 与圆相切吗?
L
O
A
L
O
A
×
×
认识新知
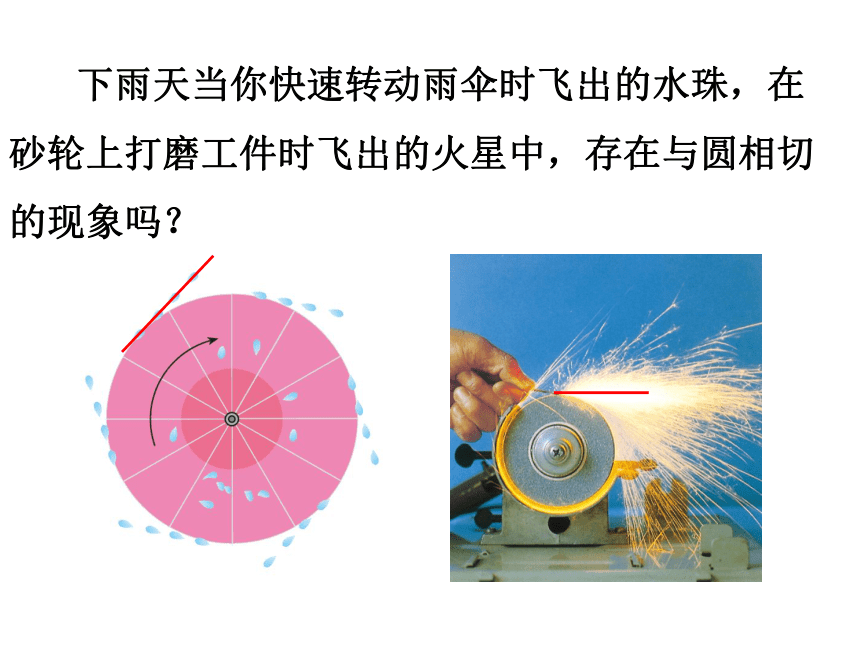
下雨天当你快速转动雨伞时飞出的水珠,在砂轮上打磨工件时飞出的火星中,存在与圆相切的现象吗?
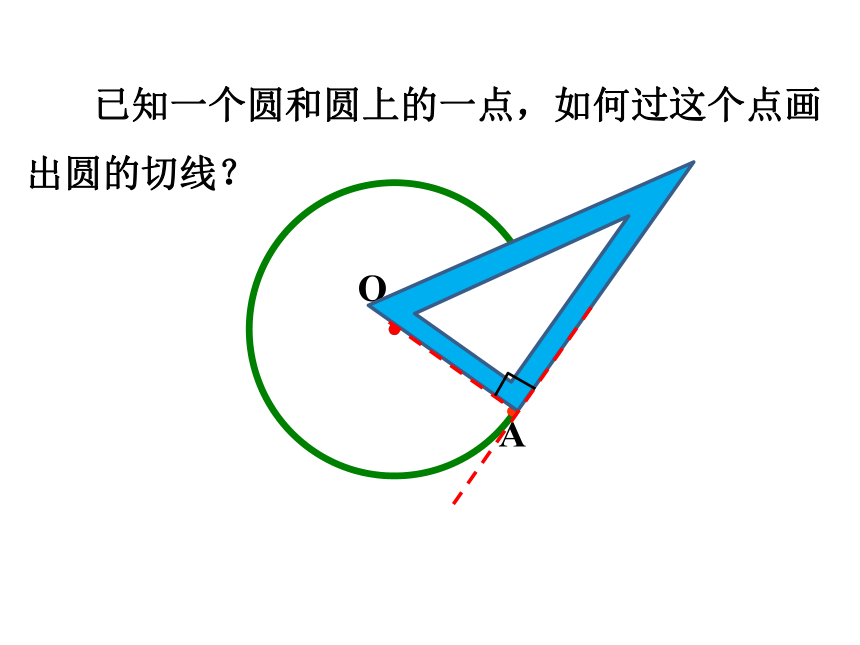
已知一个圆和圆上的一点,如何过这个点画出圆的切线?
O
A
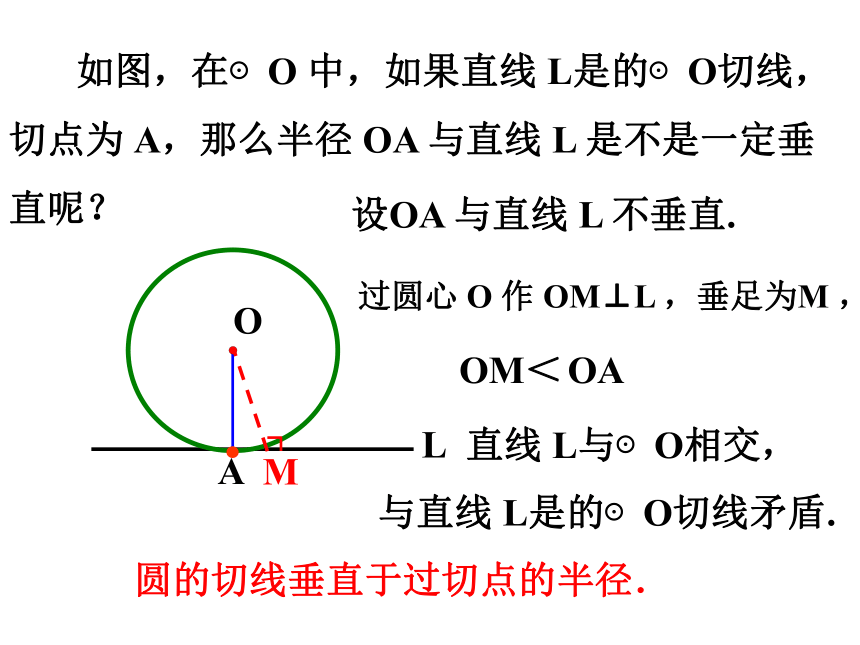
如图,在⊙O 中,如果直线 L是的⊙O切线,切点为 A,那么半径 OA 与直线 L 是不是一定垂直呢?
圆的切线垂直于过切点的半径.
L
O
A
M
OA
OM<
设OA 与直线 L 不垂直.
过圆心 O 作 OM⊥L ,垂足为M ,
直线 L与⊙O相交,
与直线 L是的⊙O切线矛盾.
1
例1 如图,AB是⊙O的直径,AC是⊙O的弦,AE交⊙O于点E,且AE⊥CP于点D,如果AC平分∠DAB.求证:直线CP与⊙O相切.
要证:
OA=OC
2
3
∠1=∠2
∠1=∠3
∠2+∠PCA=90°
直线CP与⊙O相切
∠2=∠3
连半径,证垂直
例题解析
1
如图,AB是⊙O的直径,AC是⊙O的弦,AE交⊙O于点E,且AE⊥CP于点D,如果AC平分∠DAB.求证:直线CP与⊙O相切.
连接 OC .
证明:
∵AB是⊙O的直径,
∴OA=OC,
2
3
∴∠1=∠2.
∵AE⊥CP,
∴∠3+∠PCA=90°,
∵AC平分∠DAB,
∴∠1=∠3,
∴∠2+∠PCA=90°,
∴OC⊥CP,
∴直线CP与⊙O相切.
∴∠2=∠3,
连半径,证垂直
A
B
O
D
C
例 已知:△ABC 为等腰三角形,O 是底边 BC 的中点,腰 AB 与⊙O 相切于点 D. 求证: AC 是⊙O 的切线.
过圆心 O 作 OE⊥AC ,垂足为E ,
E
OE=
OD
OA .
AC 是⊙O 的切线
连接 OD ,
A
B
O
D
C
已知:△ABC 为等腰三角形,O 是底边 BC 的中点,腰 AB 与⊙O 相切于点 D. 求证: AC 是⊙O 的切线.
过圆心 O 作 OE⊥AC ,垂足为E ,连接 OD ,OA .
∵AB=AC,
BO=CO,
∴∠BAO=∠CAO.
∴OD⊥AB.
∵AB 与⊙O 相切于点 D,
∵OE⊥AC,
∴OE=OD,
E
∴AC 是⊙O 的切线.
证明:
作垂直,等半径
如果直线与圆有交点,则连接交点与圆心得半径,证这 条半径与该直线垂直.
当直线与圆的交点个数或交点的位置不明确时,则过圆心作直线的垂线,然后证圆心到直线的距离等于圆的半径.
判定圆的切线的两种思路:
O
A
B
C
D
思路1:
概括为:连半径,证垂直.
思路2:
概括为:作垂线,证半径.
1.如图, AB是⊙O的直径,∠ABT=45°,
AT=AB.求证:AT是⊙O的切线.
O
A
T
B
证明:
∵AT=AB,
∴∠ABT=∠ATB,
∵∠ABT=45°,
∴∠ATB=45°,
∴∠TAB=90°
∴AT⊥AB.
∵AB是⊙O的直径,
∴AT是⊙O的切线.
2.如图, AB是⊙O的直径,直线L1、L2是
⊙O的切线,A,B是切点.L1,L2有怎样的
位置关系?证明你的结论.
O
A
L2
B
解:
L1
L1∥L2.
理由如下:
∵L1、L2是 ⊙O的切线,
∴L1⊥AB,
L2⊥AB,
∴∠1=90°,
∠2=90°.
∴∠1+∠2=180°,
∴L1∥L2.
1
2
(1)切线的判定定理与性质定理是什么?它们有怎样的联系?
(2)在应用切线的判定定理和性质定理时,需要注意什么?
小结
1.如图,直线L是⊙O的切线,A为切点,B是
直线L上一点,连接OB交⊙O于点C.若AB
=4,OA=3,则BC的长为( ).
A.5 B.4 C.3 D.2
O
A
L
B
C
巩固新知
D
2.如图,CD是⊙O的切线,点B为切点,CO
的延长线交⊙O于点A.若∠A=25°,则∠C
的度数为( ).
A.25° B.30° C.35° D.40°
O
A
B
C
D
3.如图,AB是⊙O的直径,AC是⊙O的切线,
切点为A.BC与⊙O交于点D,连接OD,若
∠C=50°,则∠AOD的度数为( ).
A.40° B.50° C.80° D.100°.
O
A
B
C
D
C
4.如图,已知A,B,C是⊙O上的三点,半径
OC=1,∠ABC=30°,切线DA交于OC的延
长线于点D,则DA的长为( ).
A. B. 2 C. D. .
O
A
B
C
D
2
3
3
2
C
5.如图,AB是⊙O的切线,切点为A.BO的延
长线交⊙O于点C,若∠ACB=33°,则∠B
的度数为 .
O
A
B
C
24°
见切点,连半径
6.如图,A,B是⊙O上的两点,AC是过点A的
一条直线,若∠AOB=120°,则∠CAB
的度数为 时,AC是⊙O的切线.
O
A
B
C
60°
7.如图,在△ACD中, AB=AC,∠B=30°,
以点A为圆心,以3cm为半径作⊙A ,当AB
= cm时,BC与⊙A相切.
A
B
C
6
今天作业
课本P102页第12题
课本P101页第7题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 九年级上册
24.2.2直线和圆的位置关系(2)
直线和圆相切是直线和圆的位置关系中特殊并且重要的一种,圆的切线是连接直线型与曲线型的重要桥梁,是研究三角形内切圆、切线长定理和正多边形与圆的关系的基础.
切线的判定定理与性质定理揭示了直线和圆的半径的特殊位置关系,即,切线过半径外端并与这条半径垂直.两个定理互为逆命题.切线判定定理的探究过程体现了由一般到特殊的研究方法.
课件说明
学习目标: 1.理解切线的判定定理与性质定理; 2.会应用切线的判定定理和性质定理解决简单问题.
学习重点: 切线的判定定理和性质定理的应用.
课件说明
1.直线和圆有哪些位置关系?
2.如何判断直线和圆相切?
相切
相离
相交
①直线和圆有唯一的公共点;
②圆心到直线的距离和圆的半径相等.
复习旧知
如图,在⊙O中,经过半径 OA 的外端点 A 作直线L⊥OA,则圆心 O 到直线 L的距离是多少?直线 L和⊙O有什么位置关系?
经过半径的外端并且垂直于这条半径的直线是圆的切线.
L
O
A
等于半径OA
相切
学习新知
下面图中直线 L 与圆相切吗?
L
O
A
L
O
A
×
×
认识新知
下雨天当你快速转动雨伞时飞出的水珠,在砂轮上打磨工件时飞出的火星中,存在与圆相切的现象吗?
已知一个圆和圆上的一点,如何过这个点画出圆的切线?
O
A
如图,在⊙O 中,如果直线 L是的⊙O切线,切点为 A,那么半径 OA 与直线 L 是不是一定垂直呢?
圆的切线垂直于过切点的半径.
L
O
A
M
OA
OM<
设OA 与直线 L 不垂直.
过圆心 O 作 OM⊥L ,垂足为M ,
直线 L与⊙O相交,
与直线 L是的⊙O切线矛盾.
1
例1 如图,AB是⊙O的直径,AC是⊙O的弦,AE交⊙O于点E,且AE⊥CP于点D,如果AC平分∠DAB.求证:直线CP与⊙O相切.
要证:
OA=OC
2
3
∠1=∠2
∠1=∠3
∠2+∠PCA=90°
直线CP与⊙O相切
∠2=∠3
连半径,证垂直
例题解析
1
如图,AB是⊙O的直径,AC是⊙O的弦,AE交⊙O于点E,且AE⊥CP于点D,如果AC平分∠DAB.求证:直线CP与⊙O相切.
连接 OC .
证明:
∵AB是⊙O的直径,
∴OA=OC,
2
3
∴∠1=∠2.
∵AE⊥CP,
∴∠3+∠PCA=90°,
∵AC平分∠DAB,
∴∠1=∠3,
∴∠2+∠PCA=90°,
∴OC⊥CP,
∴直线CP与⊙O相切.
∴∠2=∠3,
连半径,证垂直
A
B
O
D
C
例 已知:△ABC 为等腰三角形,O 是底边 BC 的中点,腰 AB 与⊙O 相切于点 D. 求证: AC 是⊙O 的切线.
过圆心 O 作 OE⊥AC ,垂足为E ,
E
OE=
OD
OA .
AC 是⊙O 的切线
连接 OD ,
A
B
O
D
C
已知:△ABC 为等腰三角形,O 是底边 BC 的中点,腰 AB 与⊙O 相切于点 D. 求证: AC 是⊙O 的切线.
过圆心 O 作 OE⊥AC ,垂足为E ,连接 OD ,OA .
∵AB=AC,
BO=CO,
∴∠BAO=∠CAO.
∴OD⊥AB.
∵AB 与⊙O 相切于点 D,
∵OE⊥AC,
∴OE=OD,
E
∴AC 是⊙O 的切线.
证明:
作垂直,等半径
如果直线与圆有交点,则连接交点与圆心得半径,证这 条半径与该直线垂直.
当直线与圆的交点个数或交点的位置不明确时,则过圆心作直线的垂线,然后证圆心到直线的距离等于圆的半径.
判定圆的切线的两种思路:
O
A
B
C
D
思路1:
概括为:连半径,证垂直.
思路2:
概括为:作垂线,证半径.
1.如图, AB是⊙O的直径,∠ABT=45°,
AT=AB.求证:AT是⊙O的切线.
O
A
T
B
证明:
∵AT=AB,
∴∠ABT=∠ATB,
∵∠ABT=45°,
∴∠ATB=45°,
∴∠TAB=90°
∴AT⊥AB.
∵AB是⊙O的直径,
∴AT是⊙O的切线.
2.如图, AB是⊙O的直径,直线L1、L2是
⊙O的切线,A,B是切点.L1,L2有怎样的
位置关系?证明你的结论.
O
A
L2
B
解:
L1
L1∥L2.
理由如下:
∵L1、L2是 ⊙O的切线,
∴L1⊥AB,
L2⊥AB,
∴∠1=90°,
∠2=90°.
∴∠1+∠2=180°,
∴L1∥L2.
1
2
(1)切线的判定定理与性质定理是什么?它们有怎样的联系?
(2)在应用切线的判定定理和性质定理时,需要注意什么?
小结
1.如图,直线L是⊙O的切线,A为切点,B是
直线L上一点,连接OB交⊙O于点C.若AB
=4,OA=3,则BC的长为( ).
A.5 B.4 C.3 D.2
O
A
L
B
C
巩固新知
D
2.如图,CD是⊙O的切线,点B为切点,CO
的延长线交⊙O于点A.若∠A=25°,则∠C
的度数为( ).
A.25° B.30° C.35° D.40°
O
A
B
C
D
3.如图,AB是⊙O的直径,AC是⊙O的切线,
切点为A.BC与⊙O交于点D,连接OD,若
∠C=50°,则∠AOD的度数为( ).
A.40° B.50° C.80° D.100°.
O
A
B
C
D
C
4.如图,已知A,B,C是⊙O上的三点,半径
OC=1,∠ABC=30°,切线DA交于OC的延
长线于点D,则DA的长为( ).
A. B. 2 C. D. .
O
A
B
C
D
2
3
3
2
C
5.如图,AB是⊙O的切线,切点为A.BO的延
长线交⊙O于点C,若∠ACB=33°,则∠B
的度数为 .
O
A
B
C
24°
见切点,连半径
6.如图,A,B是⊙O上的两点,AC是过点A的
一条直线,若∠AOB=120°,则∠CAB
的度数为 时,AC是⊙O的切线.
O
A
B
C
60°
7.如图,在△ACD中, AB=AC,∠B=30°,
以点A为圆心,以3cm为半径作⊙A ,当AB
= cm时,BC与⊙A相切.
A
B
C
6
今天作业
课本P102页第12题
课本P101页第7题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
