第22章 二次函数 同步讲义(无答案,pdf版)
文档属性
| 名称 | 第22章 二次函数 同步讲义(无答案,pdf版) |

|
|
| 格式 | |||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-20 00:00:00 | ||
图片预览


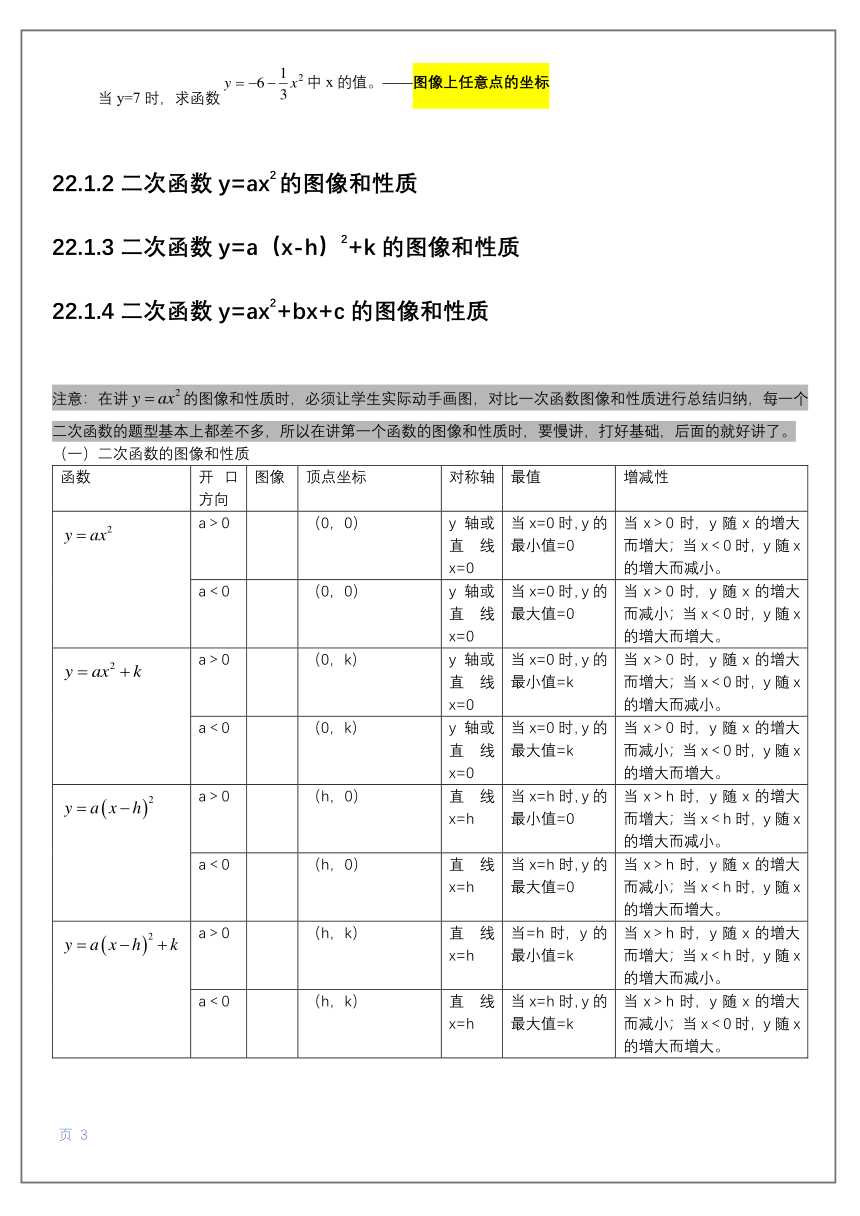
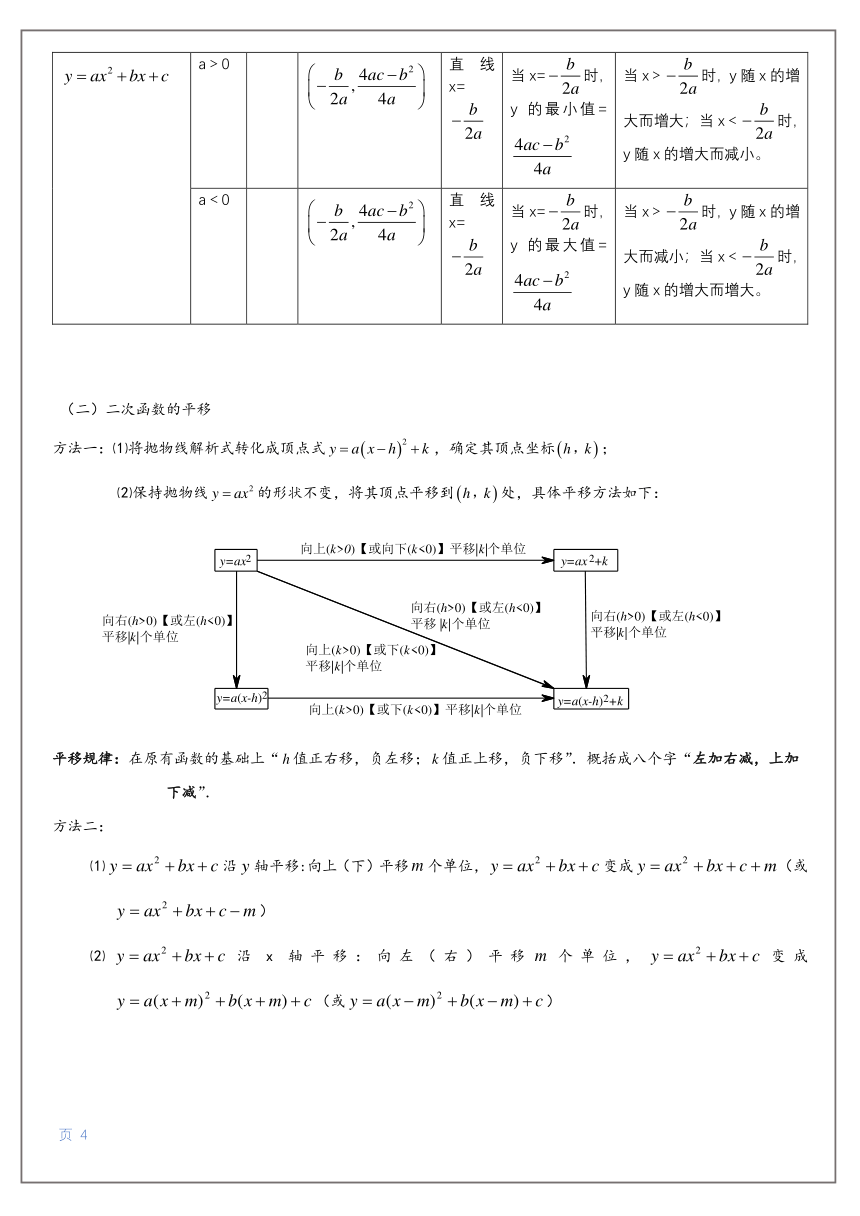

文档简介
目录
第 22 章 二次函数 .......................................................................................................................................................................................... 2
22.1 二次函数的图像和性质 ................................................................................................................................................................. 2
22.1.1 二次函数 ................................................................................................................................................................................ 2
2
22.1.2 二次函数 y=ax 的图像和性质 ........................................................................................................................................ 3
2
22.1.3 二次函数 y=a(x-h) +k 的图像和性质 .................................................................................................................... 3
2
22.1.4 二次函数 y=ax +bx+c 的图像和性质 .......................................................................................................................... 3
22.2 二次函数与一元二次方程 ............................................................................................................................................................ 9
一、二次函数与一元二次方程 ................................................................................................................................................... 9
二、二次函数与 a、b、c 的符号 ............................................................................................................................................. 12
(一)a、b、c 符号的判断 ....................................................................................................................................................... 12
(二)b2 4ac 符号的判断 ...................................................................................................................................................... 13
(三)2a+b 与 2a-b 符号判断 ................................................................................................................................................. 13
(四)常见 6 个 a、b、c 关系式符号的判断 ...................................................................................................................... 14
(五)其他代数式的判断 ........................................................................................................................................................... 14
22.3 实际应用 ........................................................................................................................................................................................... 17
(一)面积最值 ............................................................................................................................................................................. 17
(二)销售问题 ............................................................................................................................................................................. 18
(三)拱桥模型 ............................................................................................................................................................................. 19
综合大题 .................................................................................................................................................................................................... 20
页 1
第 22 章 二次函数
22.1 二次函数的图像和性质
22.1.1 二次函数
1、二次函数的概念:一般地,形如 y = ax2 + bx + c( a,b,c是常数, a 0 )的函数,叫做二次函数。
这里需要强调:和一元二次方程类似,二次项系数 a 0,而b,c 可以为零.二次函数的定义域是全体实数.
2、二次函数 y = ax2 + bx + c的结构特征:
⑴等号左边是函数,右边是关于自变量 x的二次式, x的最高次数是 2.
⑵ a,b,c是常数, a是二次项系数,且不为 0,b 是一次项系数, c 是常数项.
(3)能转化成 y = ax2 + bx + c
(4)整式
【例 1】观察:① y = 6x2 ;② y = 3x2 +5;③y=200x2+400x+200;
1 2
④ y = x3 2x; 2 2 ⑤ y = x +3; ⑥ y = (x +1) x .
x
这六个式子中二次函数有 。(只填序号)——会识别二次函数:一看指数,二看系数,三看模样
【例 2】在判断时,注意符号问题
写出上述三个例子中的 a、b、c 的值。——确定 a、b、c 的值,为后续的知识点做铺垫,再讲解时可对比一元二次
方程讲解
2
(1) y = 3x x a=______,b=______,c=______.——常数项为 0,二次项位置改变
(2)y=x2 a=______,b=______,c=______.——一次项系数和常数项为 0,二次项系数为 1
1
(3) y = x2 + 5x 10 a=______,b=______,c=______.——每一项都存在
2
1
(4) y = 6 x2 a=______,b=______,c=______.——一次项系数为 0,二次项位置改变
3
【例 3】考试常见题型
m2 2m+2
已知函数 y=m x +(m-2)x.——由系数和指数确定未知数的值
(1)若它是一次函数,则 m=______,函数的解析式是______,
(2)若它是二次函数,则 m=______,函数的解析式是______。
【例 4】当 x=4 时,求下列函数值。——给出 x 的值,求 y 的值,为求点的坐标做准备
y = 3x x2(1) (2)y=x2
1
(3) y = x2
1
+ 5x 10 (4) y = 6 x
2
2 3
【例 5】求出下列相应的 x 的值:——给出 y 值求 x 的值,为求函数与 x 轴的交点坐标和求普通的点的坐标做准备
1
y = x2 + 5x 10
当 y=0 时,求函数 2 中 x 的值。——图像与 x 轴的交点坐标
页 2
1
y = 6 x2 中 x 的值。——图像上任意点的坐标
当 y=7 时,求函数 3
22.1.2 二次函数 y=ax2的图像和性质
22.1.3 二次函数 y=a(x-h)2+k 的图像和性质
22.1.4 二次函数 y=ax2+bx+c 的图像和性质
注意:在讲 y = ax2 的图像和性质时,必须让学生实际动手画图,对比一次函数图像和性质进行总结归纳,每一个
二次函数的题型基本上都差不多,所以在讲第一个函数的图像和性质时,要慢讲,打好基础,后面的就好讲了。
(一)二次函数的图像和性质
函数 开 口 图像 顶点坐标 对称轴 最值 增减性
方向
a>0 (0,0) y 轴或 当 x=0 时,y 的 当 x>0 时,y 随 x 的增大
y = ax2
直 线 最小值=0 而增大;当 x<0 时,y 随 x
x=0 的增大而减小。
a<0 (0,0) y 轴或 当 x=0 时,y 的 当 x>0 时,y 随 x 的增大
直 线 最大值=0 而减小;当 x<0 时,y 随 x
x=0 的增大而增大。
a>0 (0,k) y 轴或 当 x=0 时,y 的 当 x>0 时,y 随 x 的增大
y = ax2 + k
直 线 最小值=k 而增大;当 x<0 时,y 随 x
x=0 的增大而减小。
a<0 (0,k) y 轴或 当 x=0 时,y 的 当 x>0 时,y 随 x 的增大
直 线 最大值=k 而减小;当 x<0 时,y 随 x
x=0 的增大而增大。
2 a>0 (h,0) 直 线 当 x=h 时,y 的 当 x>h 时,y 随 x 的增大
y = a (x h)
x=h 最小值=0 而增大;当 x<h 时,y 随 x
的增大而减小。
a<0 (h,0) 直 线 当 x=h 时,y 的 当 x>h 时,y 随 x 的增大
x=h 最大值=0 而减小;当 x<h 时,y 随 x
的增大而增大。
2 a>0 (h,k) 直 线 当=h 时,y 的 当 x>h 时,y 随 x 的增大
y = a (x h) + k
x=h 最小值=k 而增大;当 x<h 时,y 随 x
的增大而减小。
a<0 (h,k) 直 线 当 x=h 时,y 的 当 x>h 时,y 随 x 的增大
x=h 最大值=k 而减小;当 x<0 时,y 随 x
的增大而增大。
页 3
a>0 2 直 线 b b
y = ax2 +bx + c b 4ac b 当 x= 时, 当 x> 时,y 随 x 的增
, x= 2a 2a
2a 4a b y 的最小值= b
大而增大;当 x< 时,
2a 2 2a4ac b
y 随 x 的增大而减小。
4a
a<0
b 4ac b2
直 线 b b
当 x= 时, 当 x> 时,y 随 x 的增
, x= 2a 2a
2a 4a b y 的最大值= b
大而减小;当 x< 时,
2a 2 2a4ac b
y 随 x 的增大而增大。
4a
(二)二次函数的平移
2
方法一:⑴将抛物线解析式转化成顶点式 y = a(x h) + k ,确定其顶点坐标 (h,k );
⑵保持抛物线 y = ax2 的形状不变,将其顶点平移到 (h,k )处,具体平移方法如下:
向上(k>0)【或向下(k<0)】平移|k|个单位
y=ax2 y=ax 2+k
向右(h>0)【或左(h<0)】
向右(h>0)【或左(h<0)】 向右(h>0)【或左(h<0)】平移 |k|个单位
平移|k|个单位 平移|k|个单位
向上(k>0)【或下(k<0)】
平移|k|个单位
y=a(x-h)2 y=a(x-h)2+k
向上(k>0)【或下(k<0)】平移|k|个单位
平移规律:在原有函数的基础上“ h值正右移,负左移; k 值正上移,负下移”.概括成八个字“左加右减,上加
下减”.
方法二:
y = ax2⑴ + bx + c 2 2沿 y 轴平移:向上(下)平移m 个单位,y = ax + bx + c 变成 y = ax + bx + c +m(或
y = ax2 + bx + c m)
⑵ y = ax2 + bx + c 2沿 x 轴 平 移 : 向 左 ( 右 ) 平 移 m 个 单 位 , y = ax + bx + c 变 成
y = a(x +m)2 + b(x +m) + c (或 y = a(x m)2 + b(x m) + c)
页 4
【例 1】考试常见题型,一般以填空或选择题形式出现
①归纳总结图像的特征,学生必须能准确回答以下问题
②任意改变 a 的值(如负整数,负分数,正负无理数,正整数等),再次填空练习
3
①函数 y = x 2 的图象顶点是__________;对称轴是________;开口向_______;当 x=___________时,有最
7
_________值是_________;当 x 时,y 随 x 的增大而减小。——
1
②抛物线 y = x 2 9 的开口 ,对称轴是 ,顶点坐标是 ,它可以看作是由抛物线
4
1
y = x 2 向 平移 个单位得到的.
4
③抛物线 y = (x 1)2的开口 ,对称轴是 2 ,顶点坐标是 ,它可以看作是由抛物线 y = x 向
平移 个单位得到的.
1
④抛物线 y = (x + 3)2 1有最______点,其坐标是______.当 x=______时,y的最______值是______;当 x______
2
时,y随 x增大而增大.
⑤抛物线 y=2x2-3x-5 的顶点坐标为______.当 x=______时,y有最______值是______,与 x轴的交点是______,
与 y轴的交点是______,当 x______时,y随 x增大而减小,当 x______时,y随 x增大而增大.
⑥把二次函数 y=ax2+bx+c(a≠0)配方成 y=a(x-h)2+k形式为______,顶点坐标是______,对称轴是直线______.当
x=______时,y最值=______;当 a<0 时,x______时,y随 x增大而减小;x______时,y随 x增大而增大.
【例 2】根据图像和性质求值或取值范围
1、二次函数 y = (m 3)x2 的图象开口向下,则 m___________.——利用开口方向的性质与系数求值
2
【巩固 m m1】当 m= 时,抛物线 y = (m 1)x 开口向下.——利用开口方向的性质与系数、次数求值
【巩固 2】二次函数 y=(k+1)x2的图象如图所示,则 k 的取值范围为___________.——看图解题
m2 2
2、二次函数 y=mx 有最高点,则 m=___________.——利用最值求未知数的值
2
3、已知 y = (k + 2)x k +k 4 是二次函数,且当 x 0时,y 随 x 的增大而增大.——利用增减性解题
(1)求 k 的值;
(2)求顶点坐标和对称轴.
4、已知函数 y = mx2 + (m2 m)x + 2的图象关于 y 轴对称,则 m=________;
5、二次函数y mx 2 2x m 4m2的图象经过原点,则此抛物线的顶点坐标是
页 5
【例 3】二次函数 y=ax2的图象大致如下,请将图中抛物线字母的序号填入括号内.——开口大小与二次项系数的
关系,数形结合
1
(1)y=2x2如图( ); (2) y = x2 如图( ); (3)y=-x2 如图( );
2
1 1 1
(4) y = x2如图( ); (5) y = x2 如图( ); (6) y = x2 如图( ).
3 9 9
【例 4】二次函数的基础题型,学生必须会求解析式,且计算不能出错,为中考 25 题(1)奠定基础
【题型 1】待定系数法求解析式
1、若二次函数 y = ax2 的图象过点(1,-2),则 a 的值是___________。
、已知抛物线 y = ax22 + c 经过点(-3,2)、(0,-1)。求该抛物线的解析式
3、已知抛物线 y = a(x h)2经过点(-3,2)(-1,0),求抛物线的解析式。
4、已知二次函数的图象经过点 A(0,-1)、B(1,0)、C(-1,2);求该抛物线的解析式——一般式
【题型 2】先求解析式,再求点的坐标
1、已知抛物线 y = ax2 经过点(1,3),求当 y=9 时,x 的值.——先求解析式,再求点的坐标
2、二次函数 y = ax2 + c(a≠0)的图像经过 A( 21,-1),B(2,5),则函数 y = ax + c 的表达式是 。
若点 C(-2,m),D(n,7)也在这个函数的图像上,则点 C 的坐标为 ,点 D 的坐标为 。
3、二次函数 y=x2+bx+c 的图象过点 A(-2,5),且当 x=2 时,y=-3,求这个二次函数的解析式,并判断
点 B(0,3)是否在这个函数的图象上.
【题型 3】先确定二次项系数,再代点求解析式
1、形状与 y = 2x2 +3的图像形状相同,但开口方向不同,顶点坐标是(0,1)的抛物线解析式。
2
2、形状与 y = 2(x +3) 的图像形状相同,但开口方向不同,顶点坐标是(1,0)的抛物线的解析式。
【题型 4】根据顶点与对称轴求解析式
1、对称轴是 y 轴,顶点纵坐标是-3,且经过(1,2)点的解析式。
2、已知二次函数图像的顶点在 x 轴上,且图像经过(2,-2)(-1,-8),求此函数的解析式。
2 1
3、抛物线 y = ax + 2x + c 的顶点是 ( , 1),则 a 、c 的值是多少?并求出抛物线与 x 轴、y 轴的交点坐标。
3
4、已知抛物线的顶点为(1,-3),且与 y 轴交于点(0,1);
5、已知抛物线与 x 轴交于点 M(-3,0)、N(5,0),且与 y 轴交于点(0,-3);——交点式
页 6
【题型 5】利用函数的轴对称性与数形结合求函数解析式
1、如图,A、B 分别为 y = ax2 上两点,且线段 AB⊥y 轴于点(0,6),若 AB=6,则该抛物线的表达式
为 。
2 1
2、二次函数 y = a(x h) 的图象如图:已知a = ,OA=OC,试求该抛物线的解析式。
2
【例 5】二次函数 y = ax2 与直线 y = 2x 3交于点 P(1,b).——二次函数与一次函数小综合
(1)求 a、b 的值;
(2)写出二次函数的关系式,并指出 x 取何值时,该函数的 y 随 x 的增大而减小.
【巩固】函数 y = ax2 与 y = ax + b的图象可能是( )——二次函数与一次函数的图像位置关系
A. B. C. D.
【例 6】考试常考题型,一般以填空和选择题为主,为反比例函数的此类题做铺垫,反比例函数的增减性时中考的
高频考点。
1、(1)已知点 A(-2,y1),B(-4,y2)在二次函数 y=3x2的图象上,则 y1 y2.——直接带入比较大小
(2)已知点 A(2,y1),B(-3,y2),C(4,y3)在二次函数 y=ax2(a<0)的图象上,则 y1,y2,y3的大小关系是
——特殊值法比较大小
2、(1)已知点 A(2,y1),B(4,y2)在二次函数 y=-3x2+6 的图象上,则 y1 y2.
(2)已知点 A(-2,y1),B(4,y2)在二次函数 y=ax2+c(a>0)的图象上,则 y1 y2.
( 23)已知抛物线 y = 2x 1上有两点(x1,y1),(x2,y2),且 x1<x2<0,则 y1 y2(填“>”或“<”)。
3、(1)若 A(-4,y1),B(-3,y2),C(1,y 23)为二次函数 y=x +4x-5 的图象上的三点,则 y1,y2,y3 的大小关系
是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y1<y2 D.y1<y3<y2
(2)已知二次函数 y=﹣ x2﹣7x+ ,若自变量 x 分别取 x1,x2,x3,且 0<x1<x2<x3,则对应的函数值 y1,
y2,y3的大小关系正确的是【 】
A.y1>y2>y3 B.y1<y2<y3 C.y2>y3>y1 D.y2<y3<y1
页 7
【例 7】二次函数与几何综合,为中考 25 题奠定基础
抛物线 y = a(x 4)2 向左平移 6 个单位后得到抛物线 y = 3(x h)2 的图像,则 a= ,h= 。
若抛物线 y = a(x 4)2 的顶点为 A,且与 y 轴交于点 B,抛物线 y = 3(x h)2 的顶点为 M,则 S = 。 MAB
【例 8】把二次函数 y = 2x2 的图像,先沿 x 轴向左平移 6 个单位,再沿 y 轴向下平移 2 个单位,得到的图像的顶
点坐标是 。——二次函数的平移
页 8
22.2 二次函数与一元二次方程
一、二次函数与一元二次方程
(一)二次函数的交点与一元二次方程根的关系
1、对于二次函数 y = ax2 +bx + c (a 0)来说,当 y = 0 时,就得一元二次方程ax2 + bx + c = 0 (a 0),抛物线
2 2
y=ax +bx+c 与 x 轴交点的横坐标,就是一元二次方程 ax +bx+c=0 的根。
2、交点式:若一元二次方程 ax2+bx+c=0 两根为 x1,x2,则二次函数可表示为 y=_____________________.
2 x + x
3、若抛物线 y=ax +bx+c (a≠0)的图象与 x 轴有两个交点 A(x1,0)B(x2,0),则抛物线的对称轴为直线 x= 1 2 ,
2
2 2 b
2 4ac
线段 AB的距离= x1 x2 = (x1 x2 ) = (x1 + x2 ) 4x1x2 = = ,对称轴与 x 轴的交点恰为
a2 a
线段 AB 的中点。
4、抛物线 y = ax2 +bx + c 与直线 y = kx + b(当 k 0时为一次函数的图像,当 k = 0时为平行于 x 轴或与 x 轴重
合的一条直线 y = b )的交点情况.
2 x + x
5、若抛物线 y=ax +bx+c (a≠0)的图象与 x 轴有两个交点 A(x ,0)B(x ,0),则抛物线的对称轴为直线 x= 1 21 2 ,
2
b2 4ac
线段 AB的距离= x1 x2 = (x1 x2 )
2 = (x1 + x2 )
2 4x1x2 = = ,对称轴与 x 轴的交点恰为线段
a2 a
AB 的中点。
(二)二次函数与根的判别式的关系
2 2
二次函数 y=ax +bx+c (a≠0)的图象与 x 轴的交点有三种情况(也即一元二次方程 ax +bx+c=0 根的情况)
2 2
①抛物线 y=ax +bx+c( a≠0)的图象与 x 轴有两个交点(x1,0)(x2,0) <=>当△>0 时,一元二次方程 ax +bx+c=0
- b b2 4ac
(a≠0)有两个不相等的实数根 x1,x2,x1,2= ;
2a
2 b
②抛物线 y=ax +bx+c (a≠0)与 x 轴有一个交点,恰好就是抛物线的顶点(- ,0)<=>当△=0 时,方程
2a
2 b
ax +bx+c=0 有两个相等的实数根 x1=x2= -
2a
2 2
③抛物线 y=ax +bx+c (a≠0)与 x 轴没有交点<=>当△<0 时,方程 ax +bx+c=0 没有实数根。
页 9
(三)二次函数与不等式的关系
利用二次函数图象求一元二次不等式的解集:
2
①抛物线在 x 轴上方的部分所对应的 x 的取值范围就是不等式 ax +bx+c>0 的解集,即 y>0 时,x 的取值范围;
2
②抛物线在 x 轴下方的部分所对应的 x 的取值范围就是不等式 ax +bx+c<0 的解集,即 y<0 时,x 的取值范围;
【例 1】判断下列各抛物线是否与 x轴相交,如果相交,求出交点的坐标。——利用△判断二次函数与 x轴的交点
个数
(1)y=6x2-2x+1 (2)y=-15x2+14x+8 (3)y=x2-4x+4
【例 2】已知抛物线 y=ax2+bx+c的图象如图所示,则一元二次方程 ax2+bx+c=0( )
——数形结合判断方程根的情况
A.没有实根
B.只有一个实根
C.有两个实根,且一根为正,一根为负
D.有两个实根,且一根小于 1,一根大于 2
【例 3】中考 12 题其中一个类型题
函数 y=ax2+bx+c的图象如图所示,那么关于 x的方程 ax2+bx+c-3=0 的根的情况是( )
——根据函数图像判断方程根的情况
A.有两个不相等的实数根
B.有两个异号实数根
C.有两个相等的实数根
D.无实数根
【例 4】根据下表中的二次函数 y = ax2 +bx + c的自变量 x 与函数 y 的对应值,可判断该二次函数的图象与 x 轴
( ).——根据表格进行综合判断
x … 1 0 1 2 …
7 7
y … 1 2 …
4 4
A.只有一个交点 B.有两个交点,且它们分别在 y 轴两侧
C.有两个交点,且它们均在 y 轴同侧 D.无交点
【例 5】已知抛物线 y=x2-6x+a 的顶点在 x 轴上,则 a= ;若抛物线与 x 轴有两个交点,则 a 的范围
是 ;若抛物线与坐标轴有两个公共点,则 a 的范围是 ;——利用交点个数求取值范
围
页 10
【例 6】已知二次函数 y=x2-kx-2+k.——综合应用
(1)求证:不论 k 取何值时,这个二次函数 y=x2-kx-2+k 与 x 轴有两个不同的交点。
(2)如果二次函数 y=x2-kx-2+k 与 x 轴两个交点为 A、B,设此抛物线与 y 轴的交点为 C,当 k 为 6 时,求
S△ABC。
【例 7】如图,抛物线 y = ax2 + bx + c(a 0) 的对称轴是直线 x =1 ,且经过点 P ( 3, 0),则方程
ax2 +bx + c = 0(a 0) 的根为: 。——交点坐标与方程根的关系
【例 8】已知抛物线 y = x2 + px + q 与 x 轴的两个交点为(-2,0),(3,0),则 p = ,q = .——系数与交点
之间的关系,原理是一元二次方程根与系数的关系
【例 9】某一元二次方程的两个根分别为 x1=-2,x2=5,请写出一个经过点(-2,0),(5,0)两点二次函数的表达式:
______.(写出一个符合要求的即可)——开放性题
【例 10】这种题型最根本的理解是:图像与 x 轴的交点是 y 值正负的分界点
抛物线 y = x2 + bx + c的部分图象如图所示,若 y>0,则 x 的取值范围是——根据图像求范围,可以变化为 y>2
或 y<-1 等题型
A.-41 D.x<-3 或 x>1
页 11
二、二次函数与 a、b、c 的符号
(一)a、b、c 符号的判断
页 12
(二)b2 4ac符号的判断
(三)2a+b 与 2a-b 符号判断
页 13
(四)常见 6 个 a、b、c 关系式符号的判断
(五)其他代数式的判断
b
由对称轴入手,将对称轴直线 x= 整理成利用 a 表示 b 或利用 b 表示 a 的等式,例如:对称轴为 2,则
2a
b 1
=2,整理得 b=-4a 或 a= b,
2a 4
解题方法一:将这两个式子中得一个带入到六个常见得代数式中即可得到答案
解题方法二:将 b=-4a 带入到另外一个等式中(常见图像与 x 轴的交点)
页 14
【例 1】已知二次函数 y=ax2+bx+c的图象如右图所示,则( )——基础 a、b、c 符号的判断
A.a>0,c>0,b2-4ac<0
B.a>0,c<0,b2-4ac>0
C.a<0,c>0,b2-4ac<0
D.a<0,c<0,b2-4ac>0
2
【例 2】已知二次函数 y = ax +bx + c的图象如图所示,有以下结论:
①a +b+ c 0;②a b+ c 1;③abc 0;④4a 2b+ c 0
其中所有正确结论的序号是( )六个基本代数式的符号判断
A.①② B. ①③④ C.①②③ D.①②③④
【例 23】已知二次函数 y = ax +bx + c的图象如图.则下列 5 个代数式:ac, a + b + c ,4a 2b+ c ,2a +b ,
2a b 中,其值大于 0 的个数为( )——2a +b 与2a b 符号判断
A.2 B 3 C、4 D、5
2
【例4】已知二次函数y=ax +bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:
①b﹣2a=0;②abc<0;③a﹣2b+4c<0;④8a+c>0.其中正确的有【 】——其他代数式符号判断,两种方法
A.3个 B.2个 C.1个 D.0个
页 15
2
【例 5】如图,二次函数 y=ax +bx+c 的图象与 x 轴交于点 A(﹣1,0),与 y 轴的交点 B 在(0,2)与(0,3)之
间(不包括这两点),对称轴为直线 x=2.下列结论:
①abc<0;②9a+3b+c>0;③若点 M( ,y1),点 N( ,y2)是函数图象上的两点,则 y1<y2;④﹣ <a<﹣ .
其中正确结论有( )——与增减性相结合
A.1 个 B.2 个 C.3 个 D.4 个
【例 6】如图,二次函数 y=ax +bx+c(a≠0)的图象与 x 轴的正半轴相交于 A,B 两点,与 y 轴相交于点 C,对称
1
轴为直线 x=2,且 OA=OC.有下列结论:①abc<0;②3b+4c<0;③c>-1;④关于 x 的方程 a +bx+c=0 有一个根为 ,
a
其中正确的结论个数是——与一元二次方程相结合
A. 1 B. 2 C. 3 D. 4
【例 7】如图是抛物线 y=ax2+bx+c(a 0)的部分图象,其顶点坐标为 (1,n ),且与 x 轴的一个交点在点 (3,0)
和 (4,0)之间.则下列结论:
① a-b+c>0 ;②3a+b=0 ;③ b2=4a (c-n ) ; ④一元二次方程ax2+bx+cy=n-1 有两个不相等的实数根.
其中正确结论是( )
A.①②③ B.①③④ C.③④⑤ D.②③⑤
页 16
22.3 实际应用
(一)面积最值
【例 1】此题的变式较多,①花圃中间无篱笆②花圃中间增加若干篱笆③篱笆上增加门等
在一面靠墙的空地上用长为 24 米的篱笆围成中间隔有两道篱笆的花圃,设花圃的宽 AB 为 x 米,面积为 S
平方米,则
(1)求 S 与 x 的函数关系式及自变量的取值范围;
(2)当 x 取何值时,所围成的花圃面积最大,最大值是多少?
(3)若墙面的最大可用长度为 8 米,则求围成花圃的最大面积。
【例 2】小明的家门前有一块空地,空地外有一面长 10 米的围墙,为了美化生活环境,小明的爸爸准备靠墙修建一
个矩形花圃,他买回了 32 米长的不锈钢管准备作为花圃的围栏,为了浇花和赏花的方便,准备在花圃的中间再围
出一条宽为一米的通道及在左右花圃各放一个 1 米宽的门(木质).花圃的长与宽如何设计才能使花圃的面积最大?
x
【例 3】在矩形 ABCD 中,AB=6cm,BC=12cm,点 P 从点 A 出发,沿 AB 边向点 B 以 1cm/s 的速度移动,同时点
Q 从点 B 出发沿 BC 边向点 C 以 2cm/s 的速度移动,如果 P、Q 两点同时出发,分别到达 B、C 两点后就停止移
动.
(1)运动第 t 秒时,△PBQ 的面积 y(cm )是多少?
(2)此时五边形 APQCD 的面积是 S(cm ),写出 S 与 t 的函数关系式,并指出自变量的取值范围.
(3)t 为何值时 s 最小,最小值时多少?——动点面积问题
页 17
(二)销售问题
【例 1】再一道题中体现出了常见问法
某商品现在的售价为每件 60元,每星期可卖出 300件,市场调查反映:每涨价 1元,每星期少卖出 10件;每降价
1元,每星期可多卖出 20件,已知商品的进价为每件 40元,
(1)当售价为每件 65 元时,计算每星期的销售量和销售利润;
(2)设售价为每件 x 元,每星期的销售利润为 y 元,求 y 与 x 的函数关系式;
(3)商店想在每星期的销售成本不超过 1000 元的情况下,使得月销售利润达到 6000 元,销售单价应定为多少?
(4)如何定价才能使利润最大?
【例 2】二次函数与一次函数的实际应用
市“健益”超市购进一批 20 元/千克的绿色食品,如果以 30 元/千克销售,那么每天可售出 400 千克.由销售经验
知,每天销售量 y (千克) 与销售单价 x (元)
( x 30)存在如下图所示的一次函数关系式.
⑴试求出 y 与 x的函数关系式;
⑵设“健益”超市销售该绿色食品每天获得利润 P 元,当销售单价为何值时,每天可获得最大利润?最大利润是
多少?
⑶根据市场调查,该绿色食品每天可获利润不超过 4480 元, 现该超市经理要求每天利润不得低于 4180 元,
请你帮助该超市确定绿色食品销售单价 x的范围( 直接写出答案).
页 18
(三)拱桥模型
【例 1】考试常见题型,尤其是期末考试,此类题要把实际问题转换为二次函数的对应知识点,如可转换为求点的
坐标等
如图,足球场上守门员在 O处开出一高球,球从离地面 1米的 A处飞出(A在 Y轴上),运动员乙在距 O点 6米的 B
处发现球在自己头的正上方达到最高点 M,距地面约 4 米高,球落地后又一次弹起.据实验测算,足球在草坪上弹
起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的表达式.
(2)足球第一次落地点距守门员多少米?(取 4 3 7)
(3)运动员乙要抢到第二个落点,他应再向前跑多少米?(取 2 6 5)
【例 2】标准的拱桥模型题,添加了“是否通过”的题型,注意如何建系更简便
一座拱桥的轮廓是抛物线型(如图 16 所示),拱高 6m,跨度 20m,相邻两支柱间的距离均为 5m.
(1)将抛物线放在所给的直角坐标系中(如图 17 所示),求抛物线的解析式;
(2)求支柱 的长度;
(3)拱桥下地平面是双向行车道(正中间是一条宽 2m 的隔离带),其中的一条行车道能否并排行驶宽 2m、高 3m 的
三辆汽车(汽车间的间隔忽略不计)?请说明你的理由.
页 19
综合大题
【例 1】求点的坐标
已知抛物线 C: y = x2 4x ,
(1)求抛物线 C 的开口方向、对称轴和顶点坐标;
(2)将抛物线 C 向下平移,得抛物线C ,使抛物线C 的顶点落在直线 y=-x-7 上,
①求抛物线C 的解析式;
②抛物线C 与 x 轴的交点为 A,B(点 A 在点 B 的左侧),抛物线C 的对称轴与 x 轴的交点为 N,点 M 是线段 AN
上的一点,过点 M 作直线 MF⊥x 轴,交抛物线C 于点 F,点 F 关于抛物线对称轴的对称点为 D,点 P 是线段 MF
1
上一点,且MP = MF ,连接 PD,作 PE⊥PD 交 x 轴于点 E,且 PE=PD,求点 E 的坐标。
4
【例 2】周长最值(将军饮马)和面积最值(铅锤高,水平宽)(三角形和四边形)
如图,已知抛物线 y=ax2+bx+3 与 x 轴交于 A、B 两点,过点 A 的直线 l 与抛物线交于点 C,其中 A 点的坐标是
(1,0),C 点坐标是(4,3).
(1)求抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点 D,使△BCD 的周长最小?若存在,求出点 D 的坐标,若不存在,
请说明理由;
(3)若点 E 是(1)中抛物线上的一个动点,且位于直线 AC 的下方,试求△ACE 的最大面积及 E 点的坐标.
页 20
【例 3】等腰三角形存在和新函数关系式
如图,己知抛物线 y=x2+bx+c 图象经过点以(-1,0),B(0,-3),抛物线与 x 轴的另一个交点为 C.
(1)求这个抛物线的解析式:
(2)若抛物线的对称轴上有一动点 D,且△BCD为等腰三角形(CB≠CD),试求点 D 的坐标;
(3)若点 P 是直线 BC 上的一个动点(点 P 不与点 B 和点 C 重合),过点 P 作 x 轴的垂线,交抛物线于点 M,点
Q 也在直线 BC 上,且 PQ= 2 ,设点 P 的横坐标为 t,△PMQ的面积为 S,求出 S 与 t 之间的函数关系式
【例 4】平行四边形存在和动点相似三角形
如图,在矩形 OABC 中,AO=10,AB=8,沿直线 CD 折叠矩形 OABC 的一边 BC,使点 B 落在 OA 边上的点 E 处.分
别以 OC、OA 所在的直线为 x 轴、y 轴建立平面直角坐标系,抛物线 y=ax2+bx+c 经过 O、D、C 三点.
(Ⅰ)求 AD 的长及抛物线的解析式;
(Ⅱ)一动点 P 从点 E 出发,沿 EC 以每秒 2 个单位长的速度向点 C 运动,同时动点 Q 从点 C 出发,沿 CO 以每秒
1 个单位长的速度向点 O 运动,当点 P 运动到点 C 时,两点同时停止运动.设运动时间为 t 秒,当 t 为何值时,以
P、Q、C 为顶点的三角形与△ADE相似?
(Ⅲ)点 M 在抛物线上,点 N 在抛物线的对称轴上,是否存在这样的点 M 与点 N,使以 M,N,C,E 为顶点且 EC
为一边的四边形是平行四边形?若存在,请直接写出点 M 与点 N 的坐标(不写求解过程);若不存在,请说明理由.
页 21
第 22 章 二次函数 .......................................................................................................................................................................................... 2
22.1 二次函数的图像和性质 ................................................................................................................................................................. 2
22.1.1 二次函数 ................................................................................................................................................................................ 2
2
22.1.2 二次函数 y=ax 的图像和性质 ........................................................................................................................................ 3
2
22.1.3 二次函数 y=a(x-h) +k 的图像和性质 .................................................................................................................... 3
2
22.1.4 二次函数 y=ax +bx+c 的图像和性质 .......................................................................................................................... 3
22.2 二次函数与一元二次方程 ............................................................................................................................................................ 9
一、二次函数与一元二次方程 ................................................................................................................................................... 9
二、二次函数与 a、b、c 的符号 ............................................................................................................................................. 12
(一)a、b、c 符号的判断 ....................................................................................................................................................... 12
(二)b2 4ac 符号的判断 ...................................................................................................................................................... 13
(三)2a+b 与 2a-b 符号判断 ................................................................................................................................................. 13
(四)常见 6 个 a、b、c 关系式符号的判断 ...................................................................................................................... 14
(五)其他代数式的判断 ........................................................................................................................................................... 14
22.3 实际应用 ........................................................................................................................................................................................... 17
(一)面积最值 ............................................................................................................................................................................. 17
(二)销售问题 ............................................................................................................................................................................. 18
(三)拱桥模型 ............................................................................................................................................................................. 19
综合大题 .................................................................................................................................................................................................... 20
页 1
第 22 章 二次函数
22.1 二次函数的图像和性质
22.1.1 二次函数
1、二次函数的概念:一般地,形如 y = ax2 + bx + c( a,b,c是常数, a 0 )的函数,叫做二次函数。
这里需要强调:和一元二次方程类似,二次项系数 a 0,而b,c 可以为零.二次函数的定义域是全体实数.
2、二次函数 y = ax2 + bx + c的结构特征:
⑴等号左边是函数,右边是关于自变量 x的二次式, x的最高次数是 2.
⑵ a,b,c是常数, a是二次项系数,且不为 0,b 是一次项系数, c 是常数项.
(3)能转化成 y = ax2 + bx + c
(4)整式
【例 1】观察:① y = 6x2 ;② y = 3x2 +5;③y=200x2+400x+200;
1 2
④ y = x3 2x; 2 2 ⑤ y = x +3; ⑥ y = (x +1) x .
x
这六个式子中二次函数有 。(只填序号)——会识别二次函数:一看指数,二看系数,三看模样
【例 2】在判断时,注意符号问题
写出上述三个例子中的 a、b、c 的值。——确定 a、b、c 的值,为后续的知识点做铺垫,再讲解时可对比一元二次
方程讲解
2
(1) y = 3x x a=______,b=______,c=______.——常数项为 0,二次项位置改变
(2)y=x2 a=______,b=______,c=______.——一次项系数和常数项为 0,二次项系数为 1
1
(3) y = x2 + 5x 10 a=______,b=______,c=______.——每一项都存在
2
1
(4) y = 6 x2 a=______,b=______,c=______.——一次项系数为 0,二次项位置改变
3
【例 3】考试常见题型
m2 2m+2
已知函数 y=m x +(m-2)x.——由系数和指数确定未知数的值
(1)若它是一次函数,则 m=______,函数的解析式是______,
(2)若它是二次函数,则 m=______,函数的解析式是______。
【例 4】当 x=4 时,求下列函数值。——给出 x 的值,求 y 的值,为求点的坐标做准备
y = 3x x2(1) (2)y=x2
1
(3) y = x2
1
+ 5x 10 (4) y = 6 x
2
2 3
【例 5】求出下列相应的 x 的值:——给出 y 值求 x 的值,为求函数与 x 轴的交点坐标和求普通的点的坐标做准备
1
y = x2 + 5x 10
当 y=0 时,求函数 2 中 x 的值。——图像与 x 轴的交点坐标
页 2
1
y = 6 x2 中 x 的值。——图像上任意点的坐标
当 y=7 时,求函数 3
22.1.2 二次函数 y=ax2的图像和性质
22.1.3 二次函数 y=a(x-h)2+k 的图像和性质
22.1.4 二次函数 y=ax2+bx+c 的图像和性质
注意:在讲 y = ax2 的图像和性质时,必须让学生实际动手画图,对比一次函数图像和性质进行总结归纳,每一个
二次函数的题型基本上都差不多,所以在讲第一个函数的图像和性质时,要慢讲,打好基础,后面的就好讲了。
(一)二次函数的图像和性质
函数 开 口 图像 顶点坐标 对称轴 最值 增减性
方向
a>0 (0,0) y 轴或 当 x=0 时,y 的 当 x>0 时,y 随 x 的增大
y = ax2
直 线 最小值=0 而增大;当 x<0 时,y 随 x
x=0 的增大而减小。
a<0 (0,0) y 轴或 当 x=0 时,y 的 当 x>0 时,y 随 x 的增大
直 线 最大值=0 而减小;当 x<0 时,y 随 x
x=0 的增大而增大。
a>0 (0,k) y 轴或 当 x=0 时,y 的 当 x>0 时,y 随 x 的增大
y = ax2 + k
直 线 最小值=k 而增大;当 x<0 时,y 随 x
x=0 的增大而减小。
a<0 (0,k) y 轴或 当 x=0 时,y 的 当 x>0 时,y 随 x 的增大
直 线 最大值=k 而减小;当 x<0 时,y 随 x
x=0 的增大而增大。
2 a>0 (h,0) 直 线 当 x=h 时,y 的 当 x>h 时,y 随 x 的增大
y = a (x h)
x=h 最小值=0 而增大;当 x<h 时,y 随 x
的增大而减小。
a<0 (h,0) 直 线 当 x=h 时,y 的 当 x>h 时,y 随 x 的增大
x=h 最大值=0 而减小;当 x<h 时,y 随 x
的增大而增大。
2 a>0 (h,k) 直 线 当=h 时,y 的 当 x>h 时,y 随 x 的增大
y = a (x h) + k
x=h 最小值=k 而增大;当 x<h 时,y 随 x
的增大而减小。
a<0 (h,k) 直 线 当 x=h 时,y 的 当 x>h 时,y 随 x 的增大
x=h 最大值=k 而减小;当 x<0 时,y 随 x
的增大而增大。
页 3
a>0 2 直 线 b b
y = ax2 +bx + c b 4ac b 当 x= 时, 当 x> 时,y 随 x 的增
, x= 2a 2a
2a 4a b y 的最小值= b
大而增大;当 x< 时,
2a 2 2a4ac b
y 随 x 的增大而减小。
4a
a<0
b 4ac b2
直 线 b b
当 x= 时, 当 x> 时,y 随 x 的增
, x= 2a 2a
2a 4a b y 的最大值= b
大而减小;当 x< 时,
2a 2 2a4ac b
y 随 x 的增大而增大。
4a
(二)二次函数的平移
2
方法一:⑴将抛物线解析式转化成顶点式 y = a(x h) + k ,确定其顶点坐标 (h,k );
⑵保持抛物线 y = ax2 的形状不变,将其顶点平移到 (h,k )处,具体平移方法如下:
向上(k>0)【或向下(k<0)】平移|k|个单位
y=ax2 y=ax 2+k
向右(h>0)【或左(h<0)】
向右(h>0)【或左(h<0)】 向右(h>0)【或左(h<0)】平移 |k|个单位
平移|k|个单位 平移|k|个单位
向上(k>0)【或下(k<0)】
平移|k|个单位
y=a(x-h)2 y=a(x-h)2+k
向上(k>0)【或下(k<0)】平移|k|个单位
平移规律:在原有函数的基础上“ h值正右移,负左移; k 值正上移,负下移”.概括成八个字“左加右减,上加
下减”.
方法二:
y = ax2⑴ + bx + c 2 2沿 y 轴平移:向上(下)平移m 个单位,y = ax + bx + c 变成 y = ax + bx + c +m(或
y = ax2 + bx + c m)
⑵ y = ax2 + bx + c 2沿 x 轴 平 移 : 向 左 ( 右 ) 平 移 m 个 单 位 , y = ax + bx + c 变 成
y = a(x +m)2 + b(x +m) + c (或 y = a(x m)2 + b(x m) + c)
页 4
【例 1】考试常见题型,一般以填空或选择题形式出现
①归纳总结图像的特征,学生必须能准确回答以下问题
②任意改变 a 的值(如负整数,负分数,正负无理数,正整数等),再次填空练习
3
①函数 y = x 2 的图象顶点是__________;对称轴是________;开口向_______;当 x=___________时,有最
7
_________值是_________;当 x 时,y 随 x 的增大而减小。——
1
②抛物线 y = x 2 9 的开口 ,对称轴是 ,顶点坐标是 ,它可以看作是由抛物线
4
1
y = x 2 向 平移 个单位得到的.
4
③抛物线 y = (x 1)2的开口 ,对称轴是 2 ,顶点坐标是 ,它可以看作是由抛物线 y = x 向
平移 个单位得到的.
1
④抛物线 y = (x + 3)2 1有最______点,其坐标是______.当 x=______时,y的最______值是______;当 x______
2
时,y随 x增大而增大.
⑤抛物线 y=2x2-3x-5 的顶点坐标为______.当 x=______时,y有最______值是______,与 x轴的交点是______,
与 y轴的交点是______,当 x______时,y随 x增大而减小,当 x______时,y随 x增大而增大.
⑥把二次函数 y=ax2+bx+c(a≠0)配方成 y=a(x-h)2+k形式为______,顶点坐标是______,对称轴是直线______.当
x=______时,y最值=______;当 a<0 时,x______时,y随 x增大而减小;x______时,y随 x增大而增大.
【例 2】根据图像和性质求值或取值范围
1、二次函数 y = (m 3)x2 的图象开口向下,则 m___________.——利用开口方向的性质与系数求值
2
【巩固 m m1】当 m= 时,抛物线 y = (m 1)x 开口向下.——利用开口方向的性质与系数、次数求值
【巩固 2】二次函数 y=(k+1)x2的图象如图所示,则 k 的取值范围为___________.——看图解题
m2 2
2、二次函数 y=mx 有最高点,则 m=___________.——利用最值求未知数的值
2
3、已知 y = (k + 2)x k +k 4 是二次函数,且当 x 0时,y 随 x 的增大而增大.——利用增减性解题
(1)求 k 的值;
(2)求顶点坐标和对称轴.
4、已知函数 y = mx2 + (m2 m)x + 2的图象关于 y 轴对称,则 m=________;
5、二次函数y mx 2 2x m 4m2的图象经过原点,则此抛物线的顶点坐标是
页 5
【例 3】二次函数 y=ax2的图象大致如下,请将图中抛物线字母的序号填入括号内.——开口大小与二次项系数的
关系,数形结合
1
(1)y=2x2如图( ); (2) y = x2 如图( ); (3)y=-x2 如图( );
2
1 1 1
(4) y = x2如图( ); (5) y = x2 如图( ); (6) y = x2 如图( ).
3 9 9
【例 4】二次函数的基础题型,学生必须会求解析式,且计算不能出错,为中考 25 题(1)奠定基础
【题型 1】待定系数法求解析式
1、若二次函数 y = ax2 的图象过点(1,-2),则 a 的值是___________。
、已知抛物线 y = ax22 + c 经过点(-3,2)、(0,-1)。求该抛物线的解析式
3、已知抛物线 y = a(x h)2经过点(-3,2)(-1,0),求抛物线的解析式。
4、已知二次函数的图象经过点 A(0,-1)、B(1,0)、C(-1,2);求该抛物线的解析式——一般式
【题型 2】先求解析式,再求点的坐标
1、已知抛物线 y = ax2 经过点(1,3),求当 y=9 时,x 的值.——先求解析式,再求点的坐标
2、二次函数 y = ax2 + c(a≠0)的图像经过 A( 21,-1),B(2,5),则函数 y = ax + c 的表达式是 。
若点 C(-2,m),D(n,7)也在这个函数的图像上,则点 C 的坐标为 ,点 D 的坐标为 。
3、二次函数 y=x2+bx+c 的图象过点 A(-2,5),且当 x=2 时,y=-3,求这个二次函数的解析式,并判断
点 B(0,3)是否在这个函数的图象上.
【题型 3】先确定二次项系数,再代点求解析式
1、形状与 y = 2x2 +3的图像形状相同,但开口方向不同,顶点坐标是(0,1)的抛物线解析式。
2
2、形状与 y = 2(x +3) 的图像形状相同,但开口方向不同,顶点坐标是(1,0)的抛物线的解析式。
【题型 4】根据顶点与对称轴求解析式
1、对称轴是 y 轴,顶点纵坐标是-3,且经过(1,2)点的解析式。
2、已知二次函数图像的顶点在 x 轴上,且图像经过(2,-2)(-1,-8),求此函数的解析式。
2 1
3、抛物线 y = ax + 2x + c 的顶点是 ( , 1),则 a 、c 的值是多少?并求出抛物线与 x 轴、y 轴的交点坐标。
3
4、已知抛物线的顶点为(1,-3),且与 y 轴交于点(0,1);
5、已知抛物线与 x 轴交于点 M(-3,0)、N(5,0),且与 y 轴交于点(0,-3);——交点式
页 6
【题型 5】利用函数的轴对称性与数形结合求函数解析式
1、如图,A、B 分别为 y = ax2 上两点,且线段 AB⊥y 轴于点(0,6),若 AB=6,则该抛物线的表达式
为 。
2 1
2、二次函数 y = a(x h) 的图象如图:已知a = ,OA=OC,试求该抛物线的解析式。
2
【例 5】二次函数 y = ax2 与直线 y = 2x 3交于点 P(1,b).——二次函数与一次函数小综合
(1)求 a、b 的值;
(2)写出二次函数的关系式,并指出 x 取何值时,该函数的 y 随 x 的增大而减小.
【巩固】函数 y = ax2 与 y = ax + b的图象可能是( )——二次函数与一次函数的图像位置关系
A. B. C. D.
【例 6】考试常考题型,一般以填空和选择题为主,为反比例函数的此类题做铺垫,反比例函数的增减性时中考的
高频考点。
1、(1)已知点 A(-2,y1),B(-4,y2)在二次函数 y=3x2的图象上,则 y1 y2.——直接带入比较大小
(2)已知点 A(2,y1),B(-3,y2),C(4,y3)在二次函数 y=ax2(a<0)的图象上,则 y1,y2,y3的大小关系是
——特殊值法比较大小
2、(1)已知点 A(2,y1),B(4,y2)在二次函数 y=-3x2+6 的图象上,则 y1 y2.
(2)已知点 A(-2,y1),B(4,y2)在二次函数 y=ax2+c(a>0)的图象上,则 y1 y2.
( 23)已知抛物线 y = 2x 1上有两点(x1,y1),(x2,y2),且 x1<x2<0,则 y1 y2(填“>”或“<”)。
3、(1)若 A(-4,y1),B(-3,y2),C(1,y 23)为二次函数 y=x +4x-5 的图象上的三点,则 y1,y2,y3 的大小关系
是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y1<y2 D.y1<y3<y2
(2)已知二次函数 y=﹣ x2﹣7x+ ,若自变量 x 分别取 x1,x2,x3,且 0<x1<x2<x3,则对应的函数值 y1,
y2,y3的大小关系正确的是【 】
A.y1>y2>y3 B.y1<y2<y3 C.y2>y3>y1 D.y2<y3<y1
页 7
【例 7】二次函数与几何综合,为中考 25 题奠定基础
抛物线 y = a(x 4)2 向左平移 6 个单位后得到抛物线 y = 3(x h)2 的图像,则 a= ,h= 。
若抛物线 y = a(x 4)2 的顶点为 A,且与 y 轴交于点 B,抛物线 y = 3(x h)2 的顶点为 M,则 S = 。 MAB
【例 8】把二次函数 y = 2x2 的图像,先沿 x 轴向左平移 6 个单位,再沿 y 轴向下平移 2 个单位,得到的图像的顶
点坐标是 。——二次函数的平移
页 8
22.2 二次函数与一元二次方程
一、二次函数与一元二次方程
(一)二次函数的交点与一元二次方程根的关系
1、对于二次函数 y = ax2 +bx + c (a 0)来说,当 y = 0 时,就得一元二次方程ax2 + bx + c = 0 (a 0),抛物线
2 2
y=ax +bx+c 与 x 轴交点的横坐标,就是一元二次方程 ax +bx+c=0 的根。
2、交点式:若一元二次方程 ax2+bx+c=0 两根为 x1,x2,则二次函数可表示为 y=_____________________.
2 x + x
3、若抛物线 y=ax +bx+c (a≠0)的图象与 x 轴有两个交点 A(x1,0)B(x2,0),则抛物线的对称轴为直线 x= 1 2 ,
2
2 2 b
2 4ac
线段 AB的距离= x1 x2 = (x1 x2 ) = (x1 + x2 ) 4x1x2 = = ,对称轴与 x 轴的交点恰为
a2 a
线段 AB 的中点。
4、抛物线 y = ax2 +bx + c 与直线 y = kx + b(当 k 0时为一次函数的图像,当 k = 0时为平行于 x 轴或与 x 轴重
合的一条直线 y = b )的交点情况.
2 x + x
5、若抛物线 y=ax +bx+c (a≠0)的图象与 x 轴有两个交点 A(x ,0)B(x ,0),则抛物线的对称轴为直线 x= 1 21 2 ,
2
b2 4ac
线段 AB的距离= x1 x2 = (x1 x2 )
2 = (x1 + x2 )
2 4x1x2 = = ,对称轴与 x 轴的交点恰为线段
a2 a
AB 的中点。
(二)二次函数与根的判别式的关系
2 2
二次函数 y=ax +bx+c (a≠0)的图象与 x 轴的交点有三种情况(也即一元二次方程 ax +bx+c=0 根的情况)
2 2
①抛物线 y=ax +bx+c( a≠0)的图象与 x 轴有两个交点(x1,0)(x2,0) <=>当△>0 时,一元二次方程 ax +bx+c=0
- b b2 4ac
(a≠0)有两个不相等的实数根 x1,x2,x1,2= ;
2a
2 b
②抛物线 y=ax +bx+c (a≠0)与 x 轴有一个交点,恰好就是抛物线的顶点(- ,0)<=>当△=0 时,方程
2a
2 b
ax +bx+c=0 有两个相等的实数根 x1=x2= -
2a
2 2
③抛物线 y=ax +bx+c (a≠0)与 x 轴没有交点<=>当△<0 时,方程 ax +bx+c=0 没有实数根。
页 9
(三)二次函数与不等式的关系
利用二次函数图象求一元二次不等式的解集:
2
①抛物线在 x 轴上方的部分所对应的 x 的取值范围就是不等式 ax +bx+c>0 的解集,即 y>0 时,x 的取值范围;
2
②抛物线在 x 轴下方的部分所对应的 x 的取值范围就是不等式 ax +bx+c<0 的解集,即 y<0 时,x 的取值范围;
【例 1】判断下列各抛物线是否与 x轴相交,如果相交,求出交点的坐标。——利用△判断二次函数与 x轴的交点
个数
(1)y=6x2-2x+1 (2)y=-15x2+14x+8 (3)y=x2-4x+4
【例 2】已知抛物线 y=ax2+bx+c的图象如图所示,则一元二次方程 ax2+bx+c=0( )
——数形结合判断方程根的情况
A.没有实根
B.只有一个实根
C.有两个实根,且一根为正,一根为负
D.有两个实根,且一根小于 1,一根大于 2
【例 3】中考 12 题其中一个类型题
函数 y=ax2+bx+c的图象如图所示,那么关于 x的方程 ax2+bx+c-3=0 的根的情况是( )
——根据函数图像判断方程根的情况
A.有两个不相等的实数根
B.有两个异号实数根
C.有两个相等的实数根
D.无实数根
【例 4】根据下表中的二次函数 y = ax2 +bx + c的自变量 x 与函数 y 的对应值,可判断该二次函数的图象与 x 轴
( ).——根据表格进行综合判断
x … 1 0 1 2 …
7 7
y … 1 2 …
4 4
A.只有一个交点 B.有两个交点,且它们分别在 y 轴两侧
C.有两个交点,且它们均在 y 轴同侧 D.无交点
【例 5】已知抛物线 y=x2-6x+a 的顶点在 x 轴上,则 a= ;若抛物线与 x 轴有两个交点,则 a 的范围
是 ;若抛物线与坐标轴有两个公共点,则 a 的范围是 ;——利用交点个数求取值范
围
页 10
【例 6】已知二次函数 y=x2-kx-2+k.——综合应用
(1)求证:不论 k 取何值时,这个二次函数 y=x2-kx-2+k 与 x 轴有两个不同的交点。
(2)如果二次函数 y=x2-kx-2+k 与 x 轴两个交点为 A、B,设此抛物线与 y 轴的交点为 C,当 k 为 6 时,求
S△ABC。
【例 7】如图,抛物线 y = ax2 + bx + c(a 0) 的对称轴是直线 x =1 ,且经过点 P ( 3, 0),则方程
ax2 +bx + c = 0(a 0) 的根为: 。——交点坐标与方程根的关系
【例 8】已知抛物线 y = x2 + px + q 与 x 轴的两个交点为(-2,0),(3,0),则 p = ,q = .——系数与交点
之间的关系,原理是一元二次方程根与系数的关系
【例 9】某一元二次方程的两个根分别为 x1=-2,x2=5,请写出一个经过点(-2,0),(5,0)两点二次函数的表达式:
______.(写出一个符合要求的即可)——开放性题
【例 10】这种题型最根本的理解是:图像与 x 轴的交点是 y 值正负的分界点
抛物线 y = x2 + bx + c的部分图象如图所示,若 y>0,则 x 的取值范围是——根据图像求范围,可以变化为 y>2
或 y<-1 等题型
A.-4
页 11
二、二次函数与 a、b、c 的符号
(一)a、b、c 符号的判断
页 12
(二)b2 4ac符号的判断
(三)2a+b 与 2a-b 符号判断
页 13
(四)常见 6 个 a、b、c 关系式符号的判断
(五)其他代数式的判断
b
由对称轴入手,将对称轴直线 x= 整理成利用 a 表示 b 或利用 b 表示 a 的等式,例如:对称轴为 2,则
2a
b 1
=2,整理得 b=-4a 或 a= b,
2a 4
解题方法一:将这两个式子中得一个带入到六个常见得代数式中即可得到答案
解题方法二:将 b=-4a 带入到另外一个等式中(常见图像与 x 轴的交点)
页 14
【例 1】已知二次函数 y=ax2+bx+c的图象如右图所示,则( )——基础 a、b、c 符号的判断
A.a>0,c>0,b2-4ac<0
B.a>0,c<0,b2-4ac>0
C.a<0,c>0,b2-4ac<0
D.a<0,c<0,b2-4ac>0
2
【例 2】已知二次函数 y = ax +bx + c的图象如图所示,有以下结论:
①a +b+ c 0;②a b+ c 1;③abc 0;④4a 2b+ c 0
其中所有正确结论的序号是( )六个基本代数式的符号判断
A.①② B. ①③④ C.①②③ D.①②③④
【例 23】已知二次函数 y = ax +bx + c的图象如图.则下列 5 个代数式:ac, a + b + c ,4a 2b+ c ,2a +b ,
2a b 中,其值大于 0 的个数为( )——2a +b 与2a b 符号判断
A.2 B 3 C、4 D、5
2
【例4】已知二次函数y=ax +bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:
①b﹣2a=0;②abc<0;③a﹣2b+4c<0;④8a+c>0.其中正确的有【 】——其他代数式符号判断,两种方法
A.3个 B.2个 C.1个 D.0个
页 15
2
【例 5】如图,二次函数 y=ax +bx+c 的图象与 x 轴交于点 A(﹣1,0),与 y 轴的交点 B 在(0,2)与(0,3)之
间(不包括这两点),对称轴为直线 x=2.下列结论:
①abc<0;②9a+3b+c>0;③若点 M( ,y1),点 N( ,y2)是函数图象上的两点,则 y1<y2;④﹣ <a<﹣ .
其中正确结论有( )——与增减性相结合
A.1 个 B.2 个 C.3 个 D.4 个
【例 6】如图,二次函数 y=ax +bx+c(a≠0)的图象与 x 轴的正半轴相交于 A,B 两点,与 y 轴相交于点 C,对称
1
轴为直线 x=2,且 OA=OC.有下列结论:①abc<0;②3b+4c<0;③c>-1;④关于 x 的方程 a +bx+c=0 有一个根为 ,
a
其中正确的结论个数是——与一元二次方程相结合
A. 1 B. 2 C. 3 D. 4
【例 7】如图是抛物线 y=ax2+bx+c(a 0)的部分图象,其顶点坐标为 (1,n ),且与 x 轴的一个交点在点 (3,0)
和 (4,0)之间.则下列结论:
① a-b+c>0 ;②3a+b=0 ;③ b2=4a (c-n ) ; ④一元二次方程ax2+bx+cy=n-1 有两个不相等的实数根.
其中正确结论是( )
A.①②③ B.①③④ C.③④⑤ D.②③⑤
页 16
22.3 实际应用
(一)面积最值
【例 1】此题的变式较多,①花圃中间无篱笆②花圃中间增加若干篱笆③篱笆上增加门等
在一面靠墙的空地上用长为 24 米的篱笆围成中间隔有两道篱笆的花圃,设花圃的宽 AB 为 x 米,面积为 S
平方米,则
(1)求 S 与 x 的函数关系式及自变量的取值范围;
(2)当 x 取何值时,所围成的花圃面积最大,最大值是多少?
(3)若墙面的最大可用长度为 8 米,则求围成花圃的最大面积。
【例 2】小明的家门前有一块空地,空地外有一面长 10 米的围墙,为了美化生活环境,小明的爸爸准备靠墙修建一
个矩形花圃,他买回了 32 米长的不锈钢管准备作为花圃的围栏,为了浇花和赏花的方便,准备在花圃的中间再围
出一条宽为一米的通道及在左右花圃各放一个 1 米宽的门(木质).花圃的长与宽如何设计才能使花圃的面积最大?
x
【例 3】在矩形 ABCD 中,AB=6cm,BC=12cm,点 P 从点 A 出发,沿 AB 边向点 B 以 1cm/s 的速度移动,同时点
Q 从点 B 出发沿 BC 边向点 C 以 2cm/s 的速度移动,如果 P、Q 两点同时出发,分别到达 B、C 两点后就停止移
动.
(1)运动第 t 秒时,△PBQ 的面积 y(cm )是多少?
(2)此时五边形 APQCD 的面积是 S(cm ),写出 S 与 t 的函数关系式,并指出自变量的取值范围.
(3)t 为何值时 s 最小,最小值时多少?——动点面积问题
页 17
(二)销售问题
【例 1】再一道题中体现出了常见问法
某商品现在的售价为每件 60元,每星期可卖出 300件,市场调查反映:每涨价 1元,每星期少卖出 10件;每降价
1元,每星期可多卖出 20件,已知商品的进价为每件 40元,
(1)当售价为每件 65 元时,计算每星期的销售量和销售利润;
(2)设售价为每件 x 元,每星期的销售利润为 y 元,求 y 与 x 的函数关系式;
(3)商店想在每星期的销售成本不超过 1000 元的情况下,使得月销售利润达到 6000 元,销售单价应定为多少?
(4)如何定价才能使利润最大?
【例 2】二次函数与一次函数的实际应用
市“健益”超市购进一批 20 元/千克的绿色食品,如果以 30 元/千克销售,那么每天可售出 400 千克.由销售经验
知,每天销售量 y (千克) 与销售单价 x (元)
( x 30)存在如下图所示的一次函数关系式.
⑴试求出 y 与 x的函数关系式;
⑵设“健益”超市销售该绿色食品每天获得利润 P 元,当销售单价为何值时,每天可获得最大利润?最大利润是
多少?
⑶根据市场调查,该绿色食品每天可获利润不超过 4480 元, 现该超市经理要求每天利润不得低于 4180 元,
请你帮助该超市确定绿色食品销售单价 x的范围( 直接写出答案).
页 18
(三)拱桥模型
【例 1】考试常见题型,尤其是期末考试,此类题要把实际问题转换为二次函数的对应知识点,如可转换为求点的
坐标等
如图,足球场上守门员在 O处开出一高球,球从离地面 1米的 A处飞出(A在 Y轴上),运动员乙在距 O点 6米的 B
处发现球在自己头的正上方达到最高点 M,距地面约 4 米高,球落地后又一次弹起.据实验测算,足球在草坪上弹
起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的表达式.
(2)足球第一次落地点距守门员多少米?(取 4 3 7)
(3)运动员乙要抢到第二个落点,他应再向前跑多少米?(取 2 6 5)
【例 2】标准的拱桥模型题,添加了“是否通过”的题型,注意如何建系更简便
一座拱桥的轮廓是抛物线型(如图 16 所示),拱高 6m,跨度 20m,相邻两支柱间的距离均为 5m.
(1)将抛物线放在所给的直角坐标系中(如图 17 所示),求抛物线的解析式;
(2)求支柱 的长度;
(3)拱桥下地平面是双向行车道(正中间是一条宽 2m 的隔离带),其中的一条行车道能否并排行驶宽 2m、高 3m 的
三辆汽车(汽车间的间隔忽略不计)?请说明你的理由.
页 19
综合大题
【例 1】求点的坐标
已知抛物线 C: y = x2 4x ,
(1)求抛物线 C 的开口方向、对称轴和顶点坐标;
(2)将抛物线 C 向下平移,得抛物线C ,使抛物线C 的顶点落在直线 y=-x-7 上,
①求抛物线C 的解析式;
②抛物线C 与 x 轴的交点为 A,B(点 A 在点 B 的左侧),抛物线C 的对称轴与 x 轴的交点为 N,点 M 是线段 AN
上的一点,过点 M 作直线 MF⊥x 轴,交抛物线C 于点 F,点 F 关于抛物线对称轴的对称点为 D,点 P 是线段 MF
1
上一点,且MP = MF ,连接 PD,作 PE⊥PD 交 x 轴于点 E,且 PE=PD,求点 E 的坐标。
4
【例 2】周长最值(将军饮马)和面积最值(铅锤高,水平宽)(三角形和四边形)
如图,已知抛物线 y=ax2+bx+3 与 x 轴交于 A、B 两点,过点 A 的直线 l 与抛物线交于点 C,其中 A 点的坐标是
(1,0),C 点坐标是(4,3).
(1)求抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点 D,使△BCD 的周长最小?若存在,求出点 D 的坐标,若不存在,
请说明理由;
(3)若点 E 是(1)中抛物线上的一个动点,且位于直线 AC 的下方,试求△ACE 的最大面积及 E 点的坐标.
页 20
【例 3】等腰三角形存在和新函数关系式
如图,己知抛物线 y=x2+bx+c 图象经过点以(-1,0),B(0,-3),抛物线与 x 轴的另一个交点为 C.
(1)求这个抛物线的解析式:
(2)若抛物线的对称轴上有一动点 D,且△BCD为等腰三角形(CB≠CD),试求点 D 的坐标;
(3)若点 P 是直线 BC 上的一个动点(点 P 不与点 B 和点 C 重合),过点 P 作 x 轴的垂线,交抛物线于点 M,点
Q 也在直线 BC 上,且 PQ= 2 ,设点 P 的横坐标为 t,△PMQ的面积为 S,求出 S 与 t 之间的函数关系式
【例 4】平行四边形存在和动点相似三角形
如图,在矩形 OABC 中,AO=10,AB=8,沿直线 CD 折叠矩形 OABC 的一边 BC,使点 B 落在 OA 边上的点 E 处.分
别以 OC、OA 所在的直线为 x 轴、y 轴建立平面直角坐标系,抛物线 y=ax2+bx+c 经过 O、D、C 三点.
(Ⅰ)求 AD 的长及抛物线的解析式;
(Ⅱ)一动点 P 从点 E 出发,沿 EC 以每秒 2 个单位长的速度向点 C 运动,同时动点 Q 从点 C 出发,沿 CO 以每秒
1 个单位长的速度向点 O 运动,当点 P 运动到点 C 时,两点同时停止运动.设运动时间为 t 秒,当 t 为何值时,以
P、Q、C 为顶点的三角形与△ADE相似?
(Ⅲ)点 M 在抛物线上,点 N 在抛物线的对称轴上,是否存在这样的点 M 与点 N,使以 M,N,C,E 为顶点且 EC
为一边的四边形是平行四边形?若存在,请直接写出点 M 与点 N 的坐标(不写求解过程);若不存在,请说明理由.
页 21
同课章节目录
