第23章 旋转 同步讲义(无答案,pdf版)
文档属性
| 名称 | 第23章 旋转 同步讲义(无答案,pdf版) |

|
|
| 格式 | |||
| 文件大小 | 669.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-20 08:48:24 | ||
图片预览




文档简介
目录
第 23 章 旋转 ..................................................................................................................................................................... 2
23.1 图形的旋转 .......................................................................................................................................................... 2
一、相关定义 ................................................................................................................................................................ 2
二、旋转作图 ................................................................................................................................................................ 2
23.2 中心对称 .............................................................................................................................................................. 6
23.2.1 中心对称 ....................................................................................................................... 6
23.2.2 中心对称图形 .............................................................................................................. 7
23.2.3 关于原点对称的点的坐标 ....................................................................................... 8
补充题型——综合应用 ....................................................................................................................... 8
页 1
第 23 章 旋转
23.1 图形的旋转
一、相关定义
1、定义:把一个图形绕着某一点 O 转动一个角度的图形变换叫做旋转。点 O 叫做旋转中心,转动的角叫做旋转
角(如∠AOA′),如果图形上的点 A 经过旋转变为点 A′,那么,这两个点叫做这个旋转的对应点.
要点诠释:旋转的三个要素:旋转中心、旋转方向和旋转角度.
2、性质
(1)对应点到旋转中心的距离相等(OA= OA′);
(2)对应点与旋转中心所连线段的夹角等于旋转角;
(3)旋转前、后的图形全等(△ABC≌△ A B C ).
要点诠释:图形绕某一点旋转,既可以按顺时针旋转也可以按逆时针旋转.
二、旋转作图
旋转的作图: 在画旋转图形时,首先确定旋转中心,其次确定图形的关键点,再将这些关键
沿指定的方向旋转指定的角度,然后连接对应的部分,形成相应的图形.
作图的步骤:(1)连接图形中的每一个关键点与旋转中心;
(2)把连线按要求(顺时针或逆时针)绕旋转中心旋转一定的角度(旋转角);
(3)在角的一边上截取关键点到旋转中心的距离,得到各点的对应点;
页 2
【例 1】如图,将三角尺 ABC(其中∠ABC=60°,∠C=90°)绕 B 点按顺时针方向转动一个角度到 A1BC1的位置,
使得点 A,B,C1 在同一条直线上,其中旋转中心是 ,点 C 的对应点是 ,AB 的对应边
是 ,旋转角为 度.——旋转概念及三要素
A
1
C
B C
A 1
【例 2】以(第O9题为)旋转中心,把△ABC 顺时针旋转 60°,画出旋转后图形——给旋转中心与旋转角度画图,基本作图
【例 3】如图,图形(1)是由图形(2)经过旋转得到的,请画出旋转中心.——已知旋转前后的图形,找旋转中心,为旋
转最值做铺垫
【例 4】利用旋转的性质解题,注意解题前标注的三点
【题型 1】利用旋转的性质求角度
1、如图,在△ABC中,∠CAB=65°,将△ABC绕点 A旋转到△AB′C′的位置,使 CC′∥AB,则旋转角的度数在平
面内为()
A.35° B.40° C.50° D.55°
2、如图,△ABC 中,AB=4,BC=6,∠B=60°,将△ABC 沿射线 BC 的方向平移,得到△A′B′C′,再将△A′B′C′绕点
A′逆时针旋转一定角度后,点 B′恰好与点 C 重合,则平移的距离和旋转角的度数分别为( )——旋转与平移综
合解题
页 3
A.4,30° B.2,60° C.1,30° D.3,60°
3、如图,E、F 分别是正方形 ABCD 的边 BC、CD 上的点,BE=CF,连接 AE、BF.将△ABE 绕着正方形的中心
O 顺时针方向旋转到△BCF 的位置,则旋转角是( )——正方形
A.45° B.60° C.90° D.120°
4、如图,平行四边形 ABCD 绕点 A 逆时针旋转 30°,得到平行四边形 AB′C′D′(点 B′与点 B 是对应点,点 C′与点 C 是对
应点,点 D′与点 D 是对应点),点 B′恰好落在 BC 边上,则∠C 的度数等于()——平行四边形
A. 100° B. 105° C. 115° D. 120°
【题型 2】利用旋转求线段的长度
1、如图,在矩形 ABCD 中,AD =4,DC =3,将△ADC 按逆时针方向绕点 A 旋转到△AEF(点 A、B、E 在同一直线
上),连结 CF,则 CF = .——矩形
2、如图,正方形 ABCD绕点 B逆时针旋转 30°后得到正方形 BEFG,EF与 AD相交于点 H,延长 DA交 GF于点 K.若
正方形 ABCD边长为 3 ,则 HD的长为___.——正方形
页 4
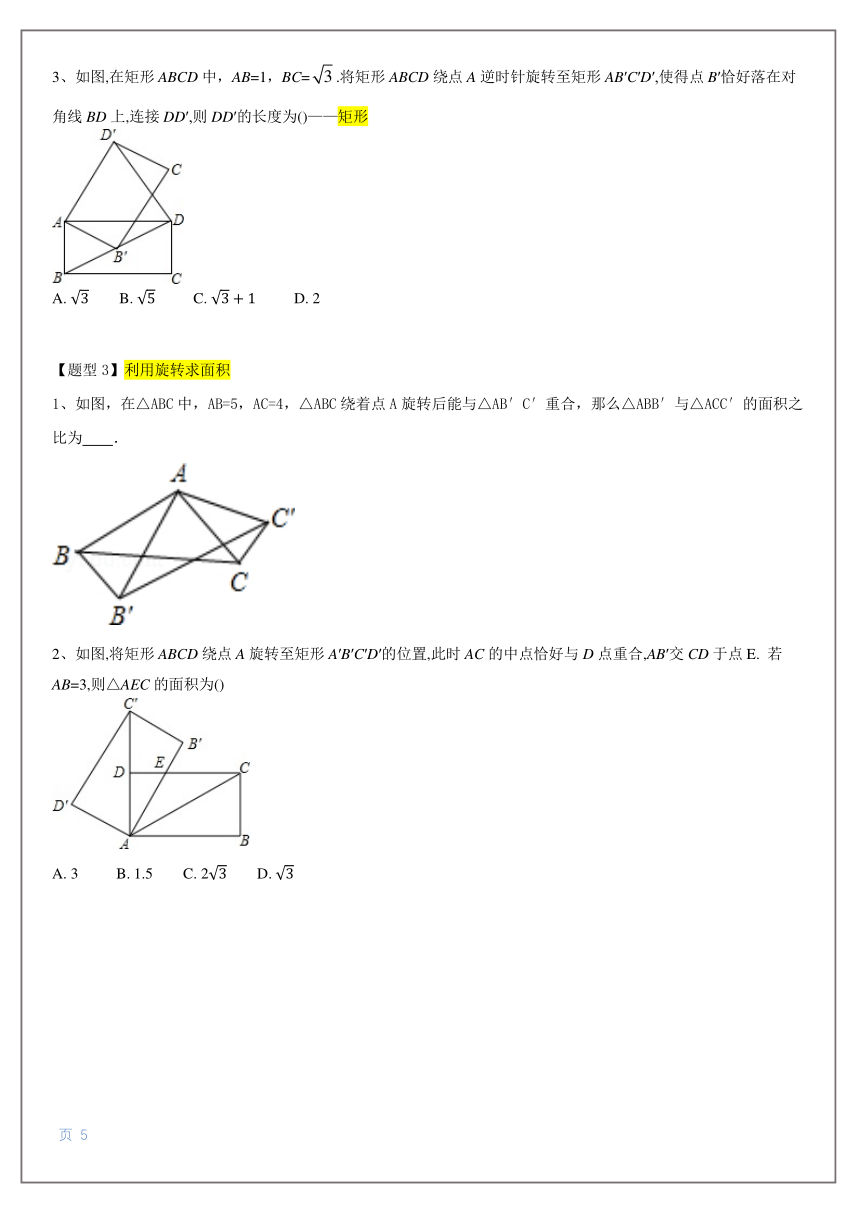
3、如图,在矩形 ABCD 中,AB=1,BC= 3 .将矩形 ABCD 绕点 A 逆时针旋转至矩形 AB′C′D′,使得点 B′恰好落在对
角线 BD 上,连接 DD′,则 DD′的长度为()——矩形
A. √3 B. √5 C. √3 + 1 D. 2
【题型 3】利用旋转求面积
1、如图,在△ABC 中,AB=5,AC=4,△ABC 绕着点 A旋转后能与△AB′C′重合,那么△ABB′与△ACC′的面积之
比为 .
2、如图,将矩形 ABCD 绕点 A 旋转至矩形 A′B′C′D′的位置,此时 AC 的中点恰好与 D 点重合,AB′交 CD 于点 E. 若
AB=3,则△AEC 的面积为()
A. 3 B. 1.5 C. 2√3 D. √3
页 5
23.2 中心对称
23.2.1 中心对称
1、定义:把一个图形绕着某一个点旋转 180°后能与另一个图形重合,那么我们就说,这两个图形成
中心对称,这个点叫对称中心,这两个图形在旋转后能重合的对应点叫对称点。
要点诠释:(1)有两个图形,能够完全重合,即形状大小都相同;
(2)位置必须满足一个条件:将其中一个图形绕着某一个点旋转 180°能够与另一个图形重合 (全等图形
不一定是中心对称的,而中心对称的两个图形一定是全等的) .
2、性质
(1)关于中心对称的两个图形是全等形。
(2)关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。
(3)关于中心对称的两个图形,对应线段平行(或在同一直线上)且相等。
3、判定:如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一
点对称。
【例1】如图,将正方形图案绕中心O旋转180°后,得到的图案是 ( )
【例 2】在一次游戏当中,小明将下面前面的四张扑克牌中的某一张旋转 180°后,得到后面四张牌的图示,小芳
看了后,很快知道小明旋转的是哪一张扑克!你知道是( )
A.黑桃 9 B.方块 J C.黑桃 8 D.梅花 3
【例 3】如图已知四边形 ABCD和点 O,求作四边形 ABCD关于 O点的对称图形。
页 6
【例 4】图中的两个四边形关于某点对称,找出它们的对称中心.
【例】如图,△ABC 与△A′B′C′关于点 O 成中心对称,下列结论中不成立的是( )
A.OC=OC′ B.OA=OA′
C.BC=B′C′ D.∠ABC=∠A′C′B′
23.2.2 中心对称图形
4、中心对称图形:把一个图形绕某一个点旋转 180°,如果旋转后的图形能够和原来的图形互相重合,
那么这个图形叫做中心对称图形,这个点就是它的对称中心。
要点诠释:(1)中心对称图形指的是一个图形;
(2)线段,平行四边形,圆等等都是中心对称图形.
【例 1】下列图形中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
【例 2】下列图案中 ,既是中心对称又是轴对称图形的是
A B C D
【例3】观察下列图案,其中旋转角最大的是 ( )
页 7
23.2.3 关于原点对称的点的坐标
两个点关于原点对称时,它们的坐标符号相反,即点 P(x,y)关于原点对称的对称点为 P1(-x,-y)。
【例 1】点 A(1,3)关于原点的对称点 A’的坐标是 ;点 P(-a,b)关于原点的对称点
P’的坐标是 ;点 A(2,n)与点 B(m,-5)关于原点对称,则 n-m= ;
直线 y=x+3 上有一点 P(m-5,2m),则 P 点关于原点的对称点 P′的坐标为____________.
【例 2】△ABC 在平面直角坐标系中的位置如图所.——网格作图求点的坐标
(1)将△ABC 绕原点 O 旋转 180°得△A1B1C1,请画出△A1B1C1 ;
(2)写出△A1B1C1中各点的坐标.
补充题型——综合应用
平移 轴对称 旋转
相同点 都是全等变换,即变换前后的图形全等.
把一个图形沿某一方 把一个图形绕着某一
定 把一个图形沿着某一条
向移动一定距离的图 定点转动一个角度的
义 直线折叠的图形变换.
形变换. 图形变换.
图
不 形
同
点
要 平移方向 旋转中心、旋转方向、
对称轴
素 平移距离 旋转角度
连接各组对应点的线 任意一对对应点所连线 对应点到旋转中心的
性 段平行(或共线)且相 段被对称轴垂直平分. 距离相等;对应点与旋
质 等. 转中心所连线段的夹
角都等于旋转角.
页 8
对应线段平行(或共 任意一对对应点所连线 *对应点到旋转中心的
线)且相等. 段被对称轴垂直平分. 距离相等;对应点与旋
转中心所连线段的夹
角等于旋转角, 即:对
应点与旋转中心连线
所成的角彼此相等.
做旋转大题时,要注意如何巧用已知的旋转角度解题
【例 1】直角三角形的旋转
在平面直角坐标系中,O 为原点,点 A(8,0),点 B(0,4),点 C,D 分别是边 OA,AB 的中点。将
△ACD 绕 点 A 顺时针方向旋转,得△AC'D',记旋转角为 α.
(I)如图①,连接 BD',当 BD'//OA 时,求点 D'的坐标;
(II)如图②,当 α=60°时,求点 C'的坐标:
(III)当点 B,D',C'共线时,求点 C 的坐标(直接写出结果即可)。
【例 2】等腰直角三角形的旋转——手拉手模型
如图 ,△ ABC 与△CDE 是等腰直角三角形,直角边 AC,CD 在同一条直线上,点M、N 分别是斜边 AB、DE
的中点,点P 为 AD 的中点,连 AE、BD、MN .
(1)求证:△ PMN 为等腰直角三角形;
(2)现将图 中的△CDE 绕着点C 顺时针旋转顺时针旋转 α(0°<α<90°),得到图②,AE与 MP、BD分别交
于点 G、H请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.
页 9
【例 3】等腰直角三角形的旋转——手拉手模型(坐标系)
在平面直角坐标系中,点 A(﹣2,0),B(2,0),C(0,2),点 D、E 分别是 AC,BC 的中点,将△CDE 绕点 C 逆
时针旋转得△CMN,点 M,N 分别是点 D,E 旋转后的对应点,记旋转角 α.
(Ⅰ)如图 1,求证 AM=BN;
(Ⅱ)如图 2,当 α=75°时,求点 N 的坐标;
(Ⅲ)当 AM∥CN,求 BN 的长(直接写出结果即可)
【例 4】等边三角形的旋转
如图①,在平面直角坐标系中,等边△ABC 的顶点 A,B 的坐标分别为(5,0),(9,0).点 D 是 x 轴正半轴上一个
动点,连接 CD,将△ACD 绕点 C 逆时针旅转 60°得到△BCE,连接 DE.
(I)直接写出点 C 的坐标,并判断△CDE 的形状,说明理由
(II)如图②,当点 D 在线段 AB 上运动时,△BDE 的周长是否存在最小值 若存在,求出△BDE 的最小周长及此
时点 D 的坐标;若不存在,说明理由:
(III)当△BDE 是直角三角形时,求点 D 的坐标。(直接写出结果即可)
页 10
【例 5】旋转最值,注意辅助圆——切线与点和圆的位置关系
3
在△ABC 中,AB=AC=5,cos∠ABC= ,将△ABC绕点 C顺时针旋转,得到△A1B1C.
5
(1)如图①,当点 B1在线段 BA延长线上时。①求证:BB1∥CA1;②求△AB1C的面积;
(2)如图②,点 E 是 BC边的中点,点 F为线段 AB上的动点,在△ABC绕点 C顺时针旋转过程中,点 F的对应点是
F1,求线段 EF1长度的最大值与最小值的差。
【例 6】正方形旋转,注意辅助圆的找法——定角对定边
在平面直角坐标系中,O为原点,点 A(-2,0),点 B(0,2),点 E,点 F分别为 OA,OB 的中点.若正方形 OEDF绕
点 O顺时针旋转,得正方形 OE′D′F′,记旋转角为α.
(Ⅰ)如图①,当α=90°,求 AE′,BF′的长;
(Ⅱ)如图②,当α=135°,求证 AE′=BF′,且 AE′⊥BF′;
(Ⅲ)若直线 AE′与直线 BF′相交于点 P,求点 P的纵坐标的最大值(直接写出结果即可)
页 11
第 23 章 旋转 ..................................................................................................................................................................... 2
23.1 图形的旋转 .......................................................................................................................................................... 2
一、相关定义 ................................................................................................................................................................ 2
二、旋转作图 ................................................................................................................................................................ 2
23.2 中心对称 .............................................................................................................................................................. 6
23.2.1 中心对称 ....................................................................................................................... 6
23.2.2 中心对称图形 .............................................................................................................. 7
23.2.3 关于原点对称的点的坐标 ....................................................................................... 8
补充题型——综合应用 ....................................................................................................................... 8
页 1
第 23 章 旋转
23.1 图形的旋转
一、相关定义
1、定义:把一个图形绕着某一点 O 转动一个角度的图形变换叫做旋转。点 O 叫做旋转中心,转动的角叫做旋转
角(如∠AOA′),如果图形上的点 A 经过旋转变为点 A′,那么,这两个点叫做这个旋转的对应点.
要点诠释:旋转的三个要素:旋转中心、旋转方向和旋转角度.
2、性质
(1)对应点到旋转中心的距离相等(OA= OA′);
(2)对应点与旋转中心所连线段的夹角等于旋转角;
(3)旋转前、后的图形全等(△ABC≌△ A B C ).
要点诠释:图形绕某一点旋转,既可以按顺时针旋转也可以按逆时针旋转.
二、旋转作图
旋转的作图: 在画旋转图形时,首先确定旋转中心,其次确定图形的关键点,再将这些关键
沿指定的方向旋转指定的角度,然后连接对应的部分,形成相应的图形.
作图的步骤:(1)连接图形中的每一个关键点与旋转中心;
(2)把连线按要求(顺时针或逆时针)绕旋转中心旋转一定的角度(旋转角);
(3)在角的一边上截取关键点到旋转中心的距离,得到各点的对应点;
页 2
【例 1】如图,将三角尺 ABC(其中∠ABC=60°,∠C=90°)绕 B 点按顺时针方向转动一个角度到 A1BC1的位置,
使得点 A,B,C1 在同一条直线上,其中旋转中心是 ,点 C 的对应点是 ,AB 的对应边
是 ,旋转角为 度.——旋转概念及三要素
A
1
C
B C
A 1
【例 2】以(第O9题为)旋转中心,把△ABC 顺时针旋转 60°,画出旋转后图形——给旋转中心与旋转角度画图,基本作图
【例 3】如图,图形(1)是由图形(2)经过旋转得到的,请画出旋转中心.——已知旋转前后的图形,找旋转中心,为旋
转最值做铺垫
【例 4】利用旋转的性质解题,注意解题前标注的三点
【题型 1】利用旋转的性质求角度
1、如图,在△ABC中,∠CAB=65°,将△ABC绕点 A旋转到△AB′C′的位置,使 CC′∥AB,则旋转角的度数在平
面内为()
A.35° B.40° C.50° D.55°
2、如图,△ABC 中,AB=4,BC=6,∠B=60°,将△ABC 沿射线 BC 的方向平移,得到△A′B′C′,再将△A′B′C′绕点
A′逆时针旋转一定角度后,点 B′恰好与点 C 重合,则平移的距离和旋转角的度数分别为( )——旋转与平移综
合解题
页 3
A.4,30° B.2,60° C.1,30° D.3,60°
3、如图,E、F 分别是正方形 ABCD 的边 BC、CD 上的点,BE=CF,连接 AE、BF.将△ABE 绕着正方形的中心
O 顺时针方向旋转到△BCF 的位置,则旋转角是( )——正方形
A.45° B.60° C.90° D.120°
4、如图,平行四边形 ABCD 绕点 A 逆时针旋转 30°,得到平行四边形 AB′C′D′(点 B′与点 B 是对应点,点 C′与点 C 是对
应点,点 D′与点 D 是对应点),点 B′恰好落在 BC 边上,则∠C 的度数等于()——平行四边形
A. 100° B. 105° C. 115° D. 120°
【题型 2】利用旋转求线段的长度
1、如图,在矩形 ABCD 中,AD =4,DC =3,将△ADC 按逆时针方向绕点 A 旋转到△AEF(点 A、B、E 在同一直线
上),连结 CF,则 CF = .——矩形
2、如图,正方形 ABCD绕点 B逆时针旋转 30°后得到正方形 BEFG,EF与 AD相交于点 H,延长 DA交 GF于点 K.若
正方形 ABCD边长为 3 ,则 HD的长为___.——正方形
页 4
3、如图,在矩形 ABCD 中,AB=1,BC= 3 .将矩形 ABCD 绕点 A 逆时针旋转至矩形 AB′C′D′,使得点 B′恰好落在对
角线 BD 上,连接 DD′,则 DD′的长度为()——矩形
A. √3 B. √5 C. √3 + 1 D. 2
【题型 3】利用旋转求面积
1、如图,在△ABC 中,AB=5,AC=4,△ABC 绕着点 A旋转后能与△AB′C′重合,那么△ABB′与△ACC′的面积之
比为 .
2、如图,将矩形 ABCD 绕点 A 旋转至矩形 A′B′C′D′的位置,此时 AC 的中点恰好与 D 点重合,AB′交 CD 于点 E. 若
AB=3,则△AEC 的面积为()
A. 3 B. 1.5 C. 2√3 D. √3
页 5
23.2 中心对称
23.2.1 中心对称
1、定义:把一个图形绕着某一个点旋转 180°后能与另一个图形重合,那么我们就说,这两个图形成
中心对称,这个点叫对称中心,这两个图形在旋转后能重合的对应点叫对称点。
要点诠释:(1)有两个图形,能够完全重合,即形状大小都相同;
(2)位置必须满足一个条件:将其中一个图形绕着某一个点旋转 180°能够与另一个图形重合 (全等图形
不一定是中心对称的,而中心对称的两个图形一定是全等的) .
2、性质
(1)关于中心对称的两个图形是全等形。
(2)关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。
(3)关于中心对称的两个图形,对应线段平行(或在同一直线上)且相等。
3、判定:如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一
点对称。
【例1】如图,将正方形图案绕中心O旋转180°后,得到的图案是 ( )
【例 2】在一次游戏当中,小明将下面前面的四张扑克牌中的某一张旋转 180°后,得到后面四张牌的图示,小芳
看了后,很快知道小明旋转的是哪一张扑克!你知道是( )
A.黑桃 9 B.方块 J C.黑桃 8 D.梅花 3
【例 3】如图已知四边形 ABCD和点 O,求作四边形 ABCD关于 O点的对称图形。
页 6
【例 4】图中的两个四边形关于某点对称,找出它们的对称中心.
【例】如图,△ABC 与△A′B′C′关于点 O 成中心对称,下列结论中不成立的是( )
A.OC=OC′ B.OA=OA′
C.BC=B′C′ D.∠ABC=∠A′C′B′
23.2.2 中心对称图形
4、中心对称图形:把一个图形绕某一个点旋转 180°,如果旋转后的图形能够和原来的图形互相重合,
那么这个图形叫做中心对称图形,这个点就是它的对称中心。
要点诠释:(1)中心对称图形指的是一个图形;
(2)线段,平行四边形,圆等等都是中心对称图形.
【例 1】下列图形中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
【例 2】下列图案中 ,既是中心对称又是轴对称图形的是
A B C D
【例3】观察下列图案,其中旋转角最大的是 ( )
页 7
23.2.3 关于原点对称的点的坐标
两个点关于原点对称时,它们的坐标符号相反,即点 P(x,y)关于原点对称的对称点为 P1(-x,-y)。
【例 1】点 A(1,3)关于原点的对称点 A’的坐标是 ;点 P(-a,b)关于原点的对称点
P’的坐标是 ;点 A(2,n)与点 B(m,-5)关于原点对称,则 n-m= ;
直线 y=x+3 上有一点 P(m-5,2m),则 P 点关于原点的对称点 P′的坐标为____________.
【例 2】△ABC 在平面直角坐标系中的位置如图所.——网格作图求点的坐标
(1)将△ABC 绕原点 O 旋转 180°得△A1B1C1,请画出△A1B1C1 ;
(2)写出△A1B1C1中各点的坐标.
补充题型——综合应用
平移 轴对称 旋转
相同点 都是全等变换,即变换前后的图形全等.
把一个图形沿某一方 把一个图形绕着某一
定 把一个图形沿着某一条
向移动一定距离的图 定点转动一个角度的
义 直线折叠的图形变换.
形变换. 图形变换.
图
不 形
同
点
要 平移方向 旋转中心、旋转方向、
对称轴
素 平移距离 旋转角度
连接各组对应点的线 任意一对对应点所连线 对应点到旋转中心的
性 段平行(或共线)且相 段被对称轴垂直平分. 距离相等;对应点与旋
质 等. 转中心所连线段的夹
角都等于旋转角.
页 8
对应线段平行(或共 任意一对对应点所连线 *对应点到旋转中心的
线)且相等. 段被对称轴垂直平分. 距离相等;对应点与旋
转中心所连线段的夹
角等于旋转角, 即:对
应点与旋转中心连线
所成的角彼此相等.
做旋转大题时,要注意如何巧用已知的旋转角度解题
【例 1】直角三角形的旋转
在平面直角坐标系中,O 为原点,点 A(8,0),点 B(0,4),点 C,D 分别是边 OA,AB 的中点。将
△ACD 绕 点 A 顺时针方向旋转,得△AC'D',记旋转角为 α.
(I)如图①,连接 BD',当 BD'//OA 时,求点 D'的坐标;
(II)如图②,当 α=60°时,求点 C'的坐标:
(III)当点 B,D',C'共线时,求点 C 的坐标(直接写出结果即可)。
【例 2】等腰直角三角形的旋转——手拉手模型
如图 ,△ ABC 与△CDE 是等腰直角三角形,直角边 AC,CD 在同一条直线上,点M、N 分别是斜边 AB、DE
的中点,点P 为 AD 的中点,连 AE、BD、MN .
(1)求证:△ PMN 为等腰直角三角形;
(2)现将图 中的△CDE 绕着点C 顺时针旋转顺时针旋转 α(0°<α<90°),得到图②,AE与 MP、BD分别交
于点 G、H请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.
页 9
【例 3】等腰直角三角形的旋转——手拉手模型(坐标系)
在平面直角坐标系中,点 A(﹣2,0),B(2,0),C(0,2),点 D、E 分别是 AC,BC 的中点,将△CDE 绕点 C 逆
时针旋转得△CMN,点 M,N 分别是点 D,E 旋转后的对应点,记旋转角 α.
(Ⅰ)如图 1,求证 AM=BN;
(Ⅱ)如图 2,当 α=75°时,求点 N 的坐标;
(Ⅲ)当 AM∥CN,求 BN 的长(直接写出结果即可)
【例 4】等边三角形的旋转
如图①,在平面直角坐标系中,等边△ABC 的顶点 A,B 的坐标分别为(5,0),(9,0).点 D 是 x 轴正半轴上一个
动点,连接 CD,将△ACD 绕点 C 逆时针旅转 60°得到△BCE,连接 DE.
(I)直接写出点 C 的坐标,并判断△CDE 的形状,说明理由
(II)如图②,当点 D 在线段 AB 上运动时,△BDE 的周长是否存在最小值 若存在,求出△BDE 的最小周长及此
时点 D 的坐标;若不存在,说明理由:
(III)当△BDE 是直角三角形时,求点 D 的坐标。(直接写出结果即可)
页 10
【例 5】旋转最值,注意辅助圆——切线与点和圆的位置关系
3
在△ABC 中,AB=AC=5,cos∠ABC= ,将△ABC绕点 C顺时针旋转,得到△A1B1C.
5
(1)如图①,当点 B1在线段 BA延长线上时。①求证:BB1∥CA1;②求△AB1C的面积;
(2)如图②,点 E 是 BC边的中点,点 F为线段 AB上的动点,在△ABC绕点 C顺时针旋转过程中,点 F的对应点是
F1,求线段 EF1长度的最大值与最小值的差。
【例 6】正方形旋转,注意辅助圆的找法——定角对定边
在平面直角坐标系中,O为原点,点 A(-2,0),点 B(0,2),点 E,点 F分别为 OA,OB 的中点.若正方形 OEDF绕
点 O顺时针旋转,得正方形 OE′D′F′,记旋转角为α.
(Ⅰ)如图①,当α=90°,求 AE′,BF′的长;
(Ⅱ)如图②,当α=135°,求证 AE′=BF′,且 AE′⊥BF′;
(Ⅲ)若直线 AE′与直线 BF′相交于点 P,求点 P的纵坐标的最大值(直接写出结果即可)
页 11
同课章节目录
