北师大版数学八年级上册 1.3勾股定理的应用 课件(共21张PPT)
文档属性
| 名称 | 北师大版数学八年级上册 1.3勾股定理的应用 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 236.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-20 08:31:29 | ||
图片预览








文档简介
(共21张PPT)
第一章 勾股定理
3 勾股定理的应用
目录
01
本课目标
02
课堂演练
本课目标
1. 能够运用勾股定理解决实际问题,体会把立体图形转化为平面图形,解决“最短路径”的问题,树立转化思想.
2. 会运用勾股定理的逆定理解决实际问题.
3. 利用数学中的“建模思想”构造直角三角形,利用勾股定理及其逆定理解决实际问题.
知识点:勾股定理的应用
解决有关勾股定理的应用问题,要从实际问题中抽象出直角三角形,然后利用勾股定理,求出其中的未知量. 其一般依据:已知直角三角形的任意两边,利用勾股定理可以求出_________.
知识重点
第三边
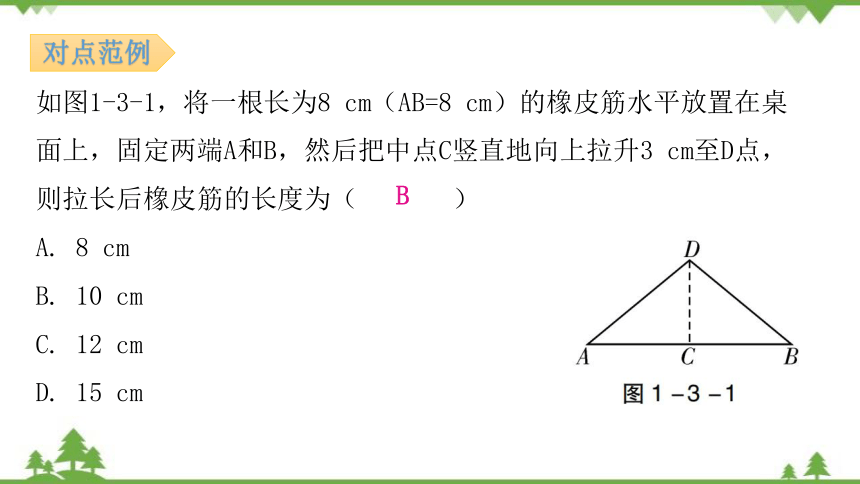
对点范例
如图1-3-1,将一根长为8 cm(AB=8 cm)的橡皮筋水平放置在桌面上,固定两端A和B,然后把中点C竖直地向上拉升3 cm至D点,则拉长后橡皮筋的长度为( )
A. 8 cm
B. 10 cm
C. 12 cm
D. 15 cm
B
课堂演练
典例精析
【例1】如图1-3-2,架在消防车上的云梯AB长为10 m,∠ADB=90°,AD∶BD=
4∶3,云梯底部离地面的距离BC为2 m,则云梯的顶端离地面的距离AE为( )
A. 8 m B. 10 m
C. 6 m D. 7 m
B
思路点拨:先利用勾股定理(a2+b2=c2)求出AD的长,再加上DE的长即为AE的长.
举一反三
1. 如图1-3-3所示是一扇高为2 m,宽为1.5 m的长方形门框,李师傅有一些薄木板要通过门框搬进屋内,在不能破坏门框,也不能锯短木板的情况下,能通过门框的
木板的最大宽度为( )
A. 1.5 m B. 2 m
C. 2.5 m D. 3 m
C
典例精析
【例2】小白兔每跳一次为1 m,先沿直线跳12次后左拐,再沿直线向前跳5次后左拐,最后沿直线向前跳13次正好回到原来的地方,则小白兔第一次左拐的角度是_________.
90°
思路点拨:利用勾股定理的逆定理可判定小白兔所走路线是一个直角三角形.
2. 为迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会,小刘搬来一架高2.5 m的木梯,准备把拉花挂到2.4 m高的墙上,则梯脚与墙角的距离应为 ( )
A. 0.7 m B. 0.8 m
C. 0.9 m D. 1.0 m
举一反三
A
典例精析
【例3】如图1-3-4所示是一个三级台阶,它的每一级的长、宽和高分别为5 dm,3 dm和1 dm,A和B是这个台阶两个相对的端点,点A处有一只蚂蚁,想到点B处吃可口的食物.请你想一想,这只蚂蚁从点A出发,沿着台阶面爬到点B的最短路程是多少?
解:如答图1-3-1,将台阶展开成平面图形后,可知AC=5 dm,BC=3×(3+1)=12(dm),∠C=90°,AB即为最短路程.
在Rt△ABC中,因为AB2=AC2+BC2,
所以AB2=52+122=132.
所以AB=13(dm).
答:这只蚂蚁从点A出发,沿着台阶面
爬到点B的最短路程是13 dm.
思路点拨:求最短路线问题,首先要将立体图形转化为平面图形,再利用勾股定理求出线段的长度.
举一反三
3. 如图1-3-5,一个圆柱形无盖玻璃容器,高18 cm,底面周长为60 cm,在外侧距下底1 cm的点C处有一只蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口1 cm的F处
有一只苍蝇,试求急于捕获苍蝇充饥的蜘
蛛所走的最短路线的长度.
解:将曲面沿AB展开,如答图1-3-3,过点C作CE⊥AB于点E,连接CF.
在Rt△CEF中,∠CEF=90°,EF=18-1-1=16(cm),
CE= ×60=30(cm),
由勾股定理,得CF2= CE2+EF2=302+162=342.
所以CF=34(cm).
答:蜘蛛所走的最短路线的长度是34 cm.
典例精析
【例4】在甲村至乙村的公路旁有一块山地正在开发,现有一处(即C处)需要爆破. 已知点C与公路上的停靠站A的距离为600 m,与公路上另一停靠站B的距离为800 m,且CA⊥CB,如图1-3-6. 为了安全起见,爆破点C周围半径400 m
范围内不得进入,则在进行爆破时,公
路AB段是否有危险,是否需要暂时封锁?
请通过计算进行说明.
解:公路AB不需要暂时封锁.理由如下.
如答图1-3-2,过点C作CD⊥AB于点D. 因为CA⊥CB,所以∠ACB=90°. 因为BC=800 m,AC=600 m,
所以,根据勾股定理可得AB=1 000(m).
因为S△ABC= AB·CD= BC·AC,
所以CD= =480(m).
由于400 m<480 m,所以没有危险.
答:公路AB段没有危险,不需要暂时封锁.
思路点拨:解题的关键是根据题设信息构造直角三角形并求出边长进行判断.
举一反三
4. “中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70 km/h.如图1-3-7,一辆小汽车在一条城市街道上直道行驶,某一时刻刚好行驶到路对面车速检测仪A的正前方60 m处的C点,过了5 s后,测得小汽车所在的B点与车速检测仪A之间的距离为100 m.
(1)求B,C间的距离;
(2)这辆小汽车超速了吗?请
说明理由.
解:(1)在Rt△ABC中,
因为AC=60 m,AB=100 m,且AB为斜边,
根据勾股定理,得AB2=AC2+BC2.
解得BC=80(m).
(2)这辆小汽车没有超速. 理由如下.
因为80÷5=16(m/s),平均速度为16 m/s,
16 m/s=57.6 km/h,
57.6<70,
所以这辆小汽车没有超速.
谢 谢
第一章 勾股定理
3 勾股定理的应用
目录
01
本课目标
02
课堂演练
本课目标
1. 能够运用勾股定理解决实际问题,体会把立体图形转化为平面图形,解决“最短路径”的问题,树立转化思想.
2. 会运用勾股定理的逆定理解决实际问题.
3. 利用数学中的“建模思想”构造直角三角形,利用勾股定理及其逆定理解决实际问题.
知识点:勾股定理的应用
解决有关勾股定理的应用问题,要从实际问题中抽象出直角三角形,然后利用勾股定理,求出其中的未知量. 其一般依据:已知直角三角形的任意两边,利用勾股定理可以求出_________.
知识重点
第三边
对点范例
如图1-3-1,将一根长为8 cm(AB=8 cm)的橡皮筋水平放置在桌面上,固定两端A和B,然后把中点C竖直地向上拉升3 cm至D点,则拉长后橡皮筋的长度为( )
A. 8 cm
B. 10 cm
C. 12 cm
D. 15 cm
B
课堂演练
典例精析
【例1】如图1-3-2,架在消防车上的云梯AB长为10 m,∠ADB=90°,AD∶BD=
4∶3,云梯底部离地面的距离BC为2 m,则云梯的顶端离地面的距离AE为( )
A. 8 m B. 10 m
C. 6 m D. 7 m
B
思路点拨:先利用勾股定理(a2+b2=c2)求出AD的长,再加上DE的长即为AE的长.
举一反三
1. 如图1-3-3所示是一扇高为2 m,宽为1.5 m的长方形门框,李师傅有一些薄木板要通过门框搬进屋内,在不能破坏门框,也不能锯短木板的情况下,能通过门框的
木板的最大宽度为( )
A. 1.5 m B. 2 m
C. 2.5 m D. 3 m
C
典例精析
【例2】小白兔每跳一次为1 m,先沿直线跳12次后左拐,再沿直线向前跳5次后左拐,最后沿直线向前跳13次正好回到原来的地方,则小白兔第一次左拐的角度是_________.
90°
思路点拨:利用勾股定理的逆定理可判定小白兔所走路线是一个直角三角形.
2. 为迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会,小刘搬来一架高2.5 m的木梯,准备把拉花挂到2.4 m高的墙上,则梯脚与墙角的距离应为 ( )
A. 0.7 m B. 0.8 m
C. 0.9 m D. 1.0 m
举一反三
A
典例精析
【例3】如图1-3-4所示是一个三级台阶,它的每一级的长、宽和高分别为5 dm,3 dm和1 dm,A和B是这个台阶两个相对的端点,点A处有一只蚂蚁,想到点B处吃可口的食物.请你想一想,这只蚂蚁从点A出发,沿着台阶面爬到点B的最短路程是多少?
解:如答图1-3-1,将台阶展开成平面图形后,可知AC=5 dm,BC=3×(3+1)=12(dm),∠C=90°,AB即为最短路程.
在Rt△ABC中,因为AB2=AC2+BC2,
所以AB2=52+122=132.
所以AB=13(dm).
答:这只蚂蚁从点A出发,沿着台阶面
爬到点B的最短路程是13 dm.
思路点拨:求最短路线问题,首先要将立体图形转化为平面图形,再利用勾股定理求出线段的长度.
举一反三
3. 如图1-3-5,一个圆柱形无盖玻璃容器,高18 cm,底面周长为60 cm,在外侧距下底1 cm的点C处有一只蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口1 cm的F处
有一只苍蝇,试求急于捕获苍蝇充饥的蜘
蛛所走的最短路线的长度.
解:将曲面沿AB展开,如答图1-3-3,过点C作CE⊥AB于点E,连接CF.
在Rt△CEF中,∠CEF=90°,EF=18-1-1=16(cm),
CE= ×60=30(cm),
由勾股定理,得CF2= CE2+EF2=302+162=342.
所以CF=34(cm).
答:蜘蛛所走的最短路线的长度是34 cm.
典例精析
【例4】在甲村至乙村的公路旁有一块山地正在开发,现有一处(即C处)需要爆破. 已知点C与公路上的停靠站A的距离为600 m,与公路上另一停靠站B的距离为800 m,且CA⊥CB,如图1-3-6. 为了安全起见,爆破点C周围半径400 m
范围内不得进入,则在进行爆破时,公
路AB段是否有危险,是否需要暂时封锁?
请通过计算进行说明.
解:公路AB不需要暂时封锁.理由如下.
如答图1-3-2,过点C作CD⊥AB于点D. 因为CA⊥CB,所以∠ACB=90°. 因为BC=800 m,AC=600 m,
所以,根据勾股定理可得AB=1 000(m).
因为S△ABC= AB·CD= BC·AC,
所以CD= =480(m).
由于400 m<480 m,所以没有危险.
答:公路AB段没有危险,不需要暂时封锁.
思路点拨:解题的关键是根据题设信息构造直角三角形并求出边长进行判断.
举一反三
4. “中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70 km/h.如图1-3-7,一辆小汽车在一条城市街道上直道行驶,某一时刻刚好行驶到路对面车速检测仪A的正前方60 m处的C点,过了5 s后,测得小汽车所在的B点与车速检测仪A之间的距离为100 m.
(1)求B,C间的距离;
(2)这辆小汽车超速了吗?请
说明理由.
解:(1)在Rt△ABC中,
因为AC=60 m,AB=100 m,且AB为斜边,
根据勾股定理,得AB2=AC2+BC2.
解得BC=80(m).
(2)这辆小汽车没有超速. 理由如下.
因为80÷5=16(m/s),平均速度为16 m/s,
16 m/s=57.6 km/h,
57.6<70,
所以这辆小汽车没有超速.
谢 谢
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
