北师大版数学八年级上册 第七章 平行线的证明 单元复习课 课件(共46张PPT)
文档属性
| 名称 | 北师大版数学八年级上册 第七章 平行线的证明 单元复习课 课件(共46张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 631.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-20 08:32:48 | ||
图片预览











文档简介
(共46张PPT)
第七章 平行线的证明
单元复习课
本章知识梳理
目录
01
课标要求
02
知识导航
课标要求
1.定义、命题、定理:
(1)通过具体实例,了解定义、命题、定理、推论的意义.
(2)结合具体实例,会区分命题的条件和结论.
(3)知道证明的意义和证明的必要性,知道证明要合乎逻辑,知道证明的过程中可以有不同的表达形式,会综合运用证明的格式.
2.探索并证明平行线的判定定理:两条直线被第三条直线所截,如果同位角相等(或内错角相等或同旁内角互补),那么这两条直线平行;探索并证明平行线的性质定理:两条平行直线被第三条直线所截,同位角相等(或内错角相等或同旁内角互补).
3.探索并证明三角形内角和定理,掌握该定理的推论:三角形的一个外角等于与它不相邻的两个内角的和.
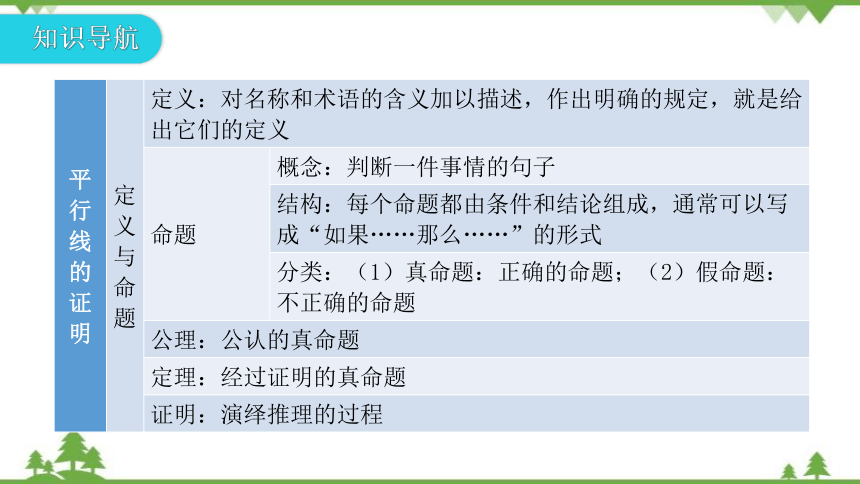
知识导航
平行线的证明 定义与命题 定义:对名称和术语的含义加以描述,作出明确的规定,就是给出它们的定义
命题 概念:判断一件事情的句子
结构:每个命题都由条件和结论组成,通常可以写成“如果……那么……”的形式
分类:(1)真命题:正确的命题;(2)假命题:不正确的命题
公理:公认的真命题
定理:经过证明的真命题
证明:演绎推理的过程
续表
平行线的证明 平行线的判定 同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
平行线的性质 两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
续表
平行线的证明 三角形内角和定理 定理:三角形的内角和等于180°
推论1:三角形的一个外角等于和它不相邻的两个内角和;
推论2:三角形的一个外角大于任何一个和它不相邻的内角
1.下列命题中,其中假命题是( )
A. 内错角相等
B. 两直线平行,同位角相等
C. 全等三角形的对应角相等
D.正方形的四个角相等
专题1 定义、命题、定理
A
2.能说明命题“对于任何实数a,|a|>-a”是假命题的一个反例可以是( )
A.a=-2 B.a=
C.a=1 D.a=
A
3.下列命题:①如果两个数的绝对值相等,那么这两个数的平方相等;②同位角相等;③在同一平面内,垂直于同一条直线的两条直线互相平行;④两个无理数的和一定是无理数;⑤坐标平面内的点与有序数对是一一对应的.其中假命题是( )
A.①③ B.②④
C.②⑤ D.①④
B
4. 用一组a,b,c的值说明命题“若a<b,则ac<bc”是错误的,这组值可以是a=______,b=_____,c=__________________.
5.下面三个命题:①底边和顶角对应相等的两个等腰三角形全等;②两边及其中一边上的中线对应相等的两个三角形全等;③斜边和斜边上的中线对应相等的两个直角三角形全等,其中正确命题的序号为_________.
6.命题“三角形的三个内角中至少有两个锐角”是_________(填“真命题”或“假命题”).
1
2
-1(答案不唯一)
①②
真命题
7. 命题“垂直于同一条直线的两条直线平行”的条件是____________________________,结论是__________________.
8.将命题“等腰三角形的两底角相等”改写成“如果……那么……”的形式__________________________________________
______________________,它是_________(填“真”或“假”)命题.
两条直线垂直于同一条直线
这两条直线平行
如果一个三角形为等腰三角形,那么这个三角形的两底角相等
真
9.按要求完成下列各题:
(1)将命题“两个钝角的和一定大于180°”写成“如果……那么……”的形式,并判断该命题是真命题还是假命题;
(2)判断命题“若a2>b2,则a>b”是真命题还是假命题,若是真命题,则举一个满足命题的例子;若是假命题,则举一个反例.
解:(1)如果两个角是钝角,那么这两个角的和一定大于180°,是真命题.
(2)是假命题,反例:当a=-2,b=-1时,a2>b2,但a10. 如图Z7-1,现有以下3句话:①AB∥CD,②∠B=∠C.③∠E=∠F.请以其中2句话为条件,第3话为结论构造命题.
(1)你构造的是哪几个命题?
(2)你构造的命题是真命题还是
假命题?请加以证明.
解:(1)由①②得到③;由①③得到②;
由②③得到①.
(2)∵AB∥CD,∴∠B=∠CDF.
又∵∠B=∠C,∴∠C=∠CDF.
∴CE∥BF.∴∠E=∠F.
所以由①②得到③为真命题.
∵AB∥CD,∴∠B=∠CDF.
∵∠E=∠F,∴CE∥BF.
∴∠C=∠CDF.∴∠B=∠C.
所以由①③得到②为真命题.
∵∠E=∠F,∴CE∥BF.∴∠C=∠CDF.
∵∠B=∠C.∴∠B=∠CDF.∴AB∥CD.
所以由②③得到①为真命题.
专题2 平行线的判定与性质
1.(2020遵义)一副直角三角板如图Z7-2所示放置,使两三角板的斜边互相平行,每块三角板的直角顶点都在另一三角板的斜边上,则∠1的度数为( )
A. 30°
B. 45°
C. 55°
D.60°
B
2. (2020湖南)如图Z7-3,已知AB∥DE,∠1=30°,∠2=35°,则∠BCE的度数为( )
A. 70°
B. 65°
C. 35°
D.5°
B
3. (2020郴州)如图Z7-4,直线a,b被直线c,d所截,下列条件能判定a∥b的是( )
A. ∠1=∠3
B. ∠2+∠4=180°
C. ∠4=∠5
D.∠1=∠2
D
4. 如图Z7-5,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠5=180°,则a∥c
C
5. (2020咸宁)如图Z7-6,请填写一个条件,使结论成立:∵____________________________,∴a∥b.
∠1=∠4(答案不唯一)
6. 如图Z7-7,∠A=70°,O是AB上一点,直线OD与AB所夹的∠BOD=78°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转_________.
8°
7.已知a,b,c为同一平面内三条不同直线,若a⊥b,c⊥b,则a与c的位置关系是_________.
8.如图Z7-8,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF,则下列结论正确的是_________(填序号).
①∠BAD+∠ADC=180°;
②AF∥DE;③∠DAF=∠F;
④若CD=DF,则DE=AF.
a∥c
①②③
9.如图Z7-9,已知AB∥CD,∠1=∠2,CF平分∠ECD.
(1)试判断直线AC与BD的位置关系,并说明理由;
(2)若∠1=80°,求∠3的度数.
解:(1)AC∥BD.理由如下.
∵AB∥CD,
∴∠2=∠CDF.
∵∠1=∠2,
∴∠1=∠CDF.
∴AC∥BD.
(2)∵∠1=80°,
∴∠ECD=180°-∠1=180°-80°=100°.
∵CF平分∠ECD,
∴∠ECF= ∠ECD= ×100°=50°.
∵AC∥BD,∴∠3=∠ECF=50°.
10.如图Z7-10,AD平分∠BAC,点E,F分别在边BC,AB上,且∠BFE=∠DAC,延长EF,CA交于点G.求证:∠G=∠AFG.
证明:∵AD平分∠BAC,
∴∠BAD=∠DAC.
∵∠BFE=∠DAC,
∴∠BFE=∠BAD.
∴EG∥AD.
∴∠G=∠DAC,∠AFG=∠FAD.
∴∠G=∠AFG.
11. 已知:如图Z7-11,∠A=∠ADE,∠C=∠E.
(1)若∠EDC=3∠C,求∠C的度数;
(2)求证:BE∥CD.
(1)解:∵∠A=∠ADE,
∴AC∥DE.
∴∠EDC+∠C=180°.
又∵∠EDC=3∠C,
∴4∠C=180°,即∠C=45°.
(2)证明:∵AC∥DE,
∴∠E=∠ABE.
又∵∠C=∠E,
∴∠C=∠ABE.
∴BE∥CD.
12.如图Z7-12,已知∠1+∠2=180°,∠B=∠3.求证:AB∥CD.
证明:∵∠1+∠2=180°,∠2+∠AFE=180°,
∴∠1=∠AFE.
∴BC∥DE.
∴∠AED=∠B.
又∵∠B=∠3,
∴∠AED=∠3.
∴AB∥CD.
13.如图Z7-13,已知∠EGB+∠CHE=180°,GM平分∠BGF,HN平分∠CHE.
(1)求证:AB∥CD;
(2)求证:∠M=∠N.
证明:(1)∵∠EGB+∠CHE=180°,∠CHE+∠EHD=180°,
∴∠EGB=∠EHD.
∴AB∥CD.
(2)∵AB∥CD,
∴∠BGF=∠CHE.
∵GM平分∠BGF,HN平分∠CHE,
∴∠NHE=∠MGF.
∴GM∥NH.
∴∠M=∠N.
专题3 三角形内角和定理及其推论
1.如图Z7-14,在△ABC中,∠B=∠C=65°,点D是BC边上任意一点,过点D作DF∥AB交AC于点E,则∠FEC的度数是( )
A. 120°
B. 130°
C. 145°
D.150°
B
2. (2020北京)如图Z7-15,AB和CD相交于点O,则下列结论正确的是( )
A. ∠1=∠2
B. ∠2=∠3
C. ∠1>∠4+∠5
D.∠2<∠5
A
3. (2020江西)如图Z7-16,∠1=∠2=65°,∠3=35°,则下列结论错误的是( )
A. AB∥CD
B. ∠B=30°
C. ∠C+∠2=∠EFC
D.CG>FG
C
4.如图Z7-17,CE是△ABC的外角∠ACD的平分线.若∠B=35°,∠ACE=60°,则∠A=( )
A.35°
B.95°
C.85°
D.75°
C
5.如图Z7-18,点D在BC的延长线上,DE⊥AB于点E,交AC于点F.若∠A=35°,∠D=15°,则∠ACB的度数为( )
A.65°
B.70°
C.75°
D.85°
B
6. (2020杭州)如图Z7-19,AB∥CD,EF分别与AB,CD交于点B,F.若∠E=30°,∠EFC=130°,则∠A=_________.
20°
7. 一副透明的三角板,如图Z7-20所示叠放,直角三角板的斜边AB,CE相交于点D,则∠BDC=_________.
75°
8.如图Z7-21,在△ABC中,∠B=56°,∠C=34°,AD为△ABC的角平分线,延长DA至点E,过点E作EH⊥BC,垂足为点H,则∠E=_________.
11°
9.如图Z7-22,在△ABC中,∠1= ∠ABC,∠2= ∠ACB,∠BDC=130°,求∠A的度数.
解:∵∠BDC=130°,
∴∠1+∠2=50°.
∵∠ABC=3∠1,
∠ACB=3∠2,
∴∠ABC+∠ACB=150°.
∴∠A=180°-∠ABC-∠ACB=30°.
10.如图Z7-23,点E在AC上,点F在AB上,BE与CF交于点O,且∠C=2∠B,∠BFC比∠BEC大20°.
(1)求∠C的度数;
(2)若∠A=70°,求∠BEC的度数.
解:(1)由三角形外角的性质可知,∠BFC=∠A+∠C,∠BEC=∠A+∠B.
由题意,得∠A+∠C=∠A+∠B+20°,且∠C=2∠B,
则∠C= ∠C+20°.
解得∠C=40°.
(2)由(1)得∠B= ∠C=20°,
∴∠BEC=∠A+∠B=90°.
11. 如图Z7-24,在△ABC中,∠BAC=90°,BD平分∠ABC,CD∥AB交BD于点D,已知∠D=29°,求∠1的度数.
解:∵CD∥AB,∠D=29°,
∴∠ABD=∠D=29°.
又∵BD平分∠ABC,
∴∠ABC=2∠ABD=58°.
∴∠1=180°-∠BAC-∠ABC
=180°-90°-58°
=32°.
12.如图Z7-25,在△ABC中,∠A=80°,∠B=30°,CD平分∠ACB,DE∥AC.
(1)求∠DEB的度数;
(2)求∠BDC的度数.
解:(1)在△ABC中,∠A=80°,∠B=30°,
∴∠ACB=180°-80°-30°=70°.
又∵DE∥AC,
∴∠DEB=∠ACB=70°.
(2)∵CD平分∠ACB,∠ACB=70°,
∴∠ACD=∠ECD= ∠ACB=35°.
∴∠BDC=180°-∠B-∠ECD
=180°-30°-35°
=115°.
13. 如图Z7-26,在△ABC中,点D在BC上,点E在AC上,AD交BE于点F.已知EG∥AD交BC于点G,EH⊥BE交BC于点H,∠HEG=50°.
(1)求∠BFD的度数;
(2)若∠BAD=∠EBC,∠C=41°,
求∠BAC的度数.
解:(1)∵EH⊥BE,
∴∠BEH=90°.
∵∠HEG=50°,
∴∠BEG=40°.
∵EG∥AD,
∴∠BFD=∠BEG=40°.
(2)∵∠BFD=∠BAD+∠ABE,∠BAD=∠EBC,
∴∠BFD=∠EBC+∠ABE=∠ABC=40°.
∵∠C=41°,
∴∠BAC=180°-∠ABC-∠C
=180°-40°-41°
=99°.
谢 谢
第七章 平行线的证明
单元复习课
本章知识梳理
目录
01
课标要求
02
知识导航
课标要求
1.定义、命题、定理:
(1)通过具体实例,了解定义、命题、定理、推论的意义.
(2)结合具体实例,会区分命题的条件和结论.
(3)知道证明的意义和证明的必要性,知道证明要合乎逻辑,知道证明的过程中可以有不同的表达形式,会综合运用证明的格式.
2.探索并证明平行线的判定定理:两条直线被第三条直线所截,如果同位角相等(或内错角相等或同旁内角互补),那么这两条直线平行;探索并证明平行线的性质定理:两条平行直线被第三条直线所截,同位角相等(或内错角相等或同旁内角互补).
3.探索并证明三角形内角和定理,掌握该定理的推论:三角形的一个外角等于与它不相邻的两个内角的和.
知识导航
平行线的证明 定义与命题 定义:对名称和术语的含义加以描述,作出明确的规定,就是给出它们的定义
命题 概念:判断一件事情的句子
结构:每个命题都由条件和结论组成,通常可以写成“如果……那么……”的形式
分类:(1)真命题:正确的命题;(2)假命题:不正确的命题
公理:公认的真命题
定理:经过证明的真命题
证明:演绎推理的过程
续表
平行线的证明 平行线的判定 同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
平行线的性质 两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
续表
平行线的证明 三角形内角和定理 定理:三角形的内角和等于180°
推论1:三角形的一个外角等于和它不相邻的两个内角和;
推论2:三角形的一个外角大于任何一个和它不相邻的内角
1.下列命题中,其中假命题是( )
A. 内错角相等
B. 两直线平行,同位角相等
C. 全等三角形的对应角相等
D.正方形的四个角相等
专题1 定义、命题、定理
A
2.能说明命题“对于任何实数a,|a|>-a”是假命题的一个反例可以是( )
A.a=-2 B.a=
C.a=1 D.a=
A
3.下列命题:①如果两个数的绝对值相等,那么这两个数的平方相等;②同位角相等;③在同一平面内,垂直于同一条直线的两条直线互相平行;④两个无理数的和一定是无理数;⑤坐标平面内的点与有序数对是一一对应的.其中假命题是( )
A.①③ B.②④
C.②⑤ D.①④
B
4. 用一组a,b,c的值说明命题“若a<b,则ac<bc”是错误的,这组值可以是a=______,b=_____,c=__________________.
5.下面三个命题:①底边和顶角对应相等的两个等腰三角形全等;②两边及其中一边上的中线对应相等的两个三角形全等;③斜边和斜边上的中线对应相等的两个直角三角形全等,其中正确命题的序号为_________.
6.命题“三角形的三个内角中至少有两个锐角”是_________(填“真命题”或“假命题”).
1
2
-1(答案不唯一)
①②
真命题
7. 命题“垂直于同一条直线的两条直线平行”的条件是____________________________,结论是__________________.
8.将命题“等腰三角形的两底角相等”改写成“如果……那么……”的形式__________________________________________
______________________,它是_________(填“真”或“假”)命题.
两条直线垂直于同一条直线
这两条直线平行
如果一个三角形为等腰三角形,那么这个三角形的两底角相等
真
9.按要求完成下列各题:
(1)将命题“两个钝角的和一定大于180°”写成“如果……那么……”的形式,并判断该命题是真命题还是假命题;
(2)判断命题“若a2>b2,则a>b”是真命题还是假命题,若是真命题,则举一个满足命题的例子;若是假命题,则举一个反例.
解:(1)如果两个角是钝角,那么这两个角的和一定大于180°,是真命题.
(2)是假命题,反例:当a=-2,b=-1时,a2>b2,但a
(1)你构造的是哪几个命题?
(2)你构造的命题是真命题还是
假命题?请加以证明.
解:(1)由①②得到③;由①③得到②;
由②③得到①.
(2)∵AB∥CD,∴∠B=∠CDF.
又∵∠B=∠C,∴∠C=∠CDF.
∴CE∥BF.∴∠E=∠F.
所以由①②得到③为真命题.
∵AB∥CD,∴∠B=∠CDF.
∵∠E=∠F,∴CE∥BF.
∴∠C=∠CDF.∴∠B=∠C.
所以由①③得到②为真命题.
∵∠E=∠F,∴CE∥BF.∴∠C=∠CDF.
∵∠B=∠C.∴∠B=∠CDF.∴AB∥CD.
所以由②③得到①为真命题.
专题2 平行线的判定与性质
1.(2020遵义)一副直角三角板如图Z7-2所示放置,使两三角板的斜边互相平行,每块三角板的直角顶点都在另一三角板的斜边上,则∠1的度数为( )
A. 30°
B. 45°
C. 55°
D.60°
B
2. (2020湖南)如图Z7-3,已知AB∥DE,∠1=30°,∠2=35°,则∠BCE的度数为( )
A. 70°
B. 65°
C. 35°
D.5°
B
3. (2020郴州)如图Z7-4,直线a,b被直线c,d所截,下列条件能判定a∥b的是( )
A. ∠1=∠3
B. ∠2+∠4=180°
C. ∠4=∠5
D.∠1=∠2
D
4. 如图Z7-5,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠5=180°,则a∥c
C
5. (2020咸宁)如图Z7-6,请填写一个条件,使结论成立:∵____________________________,∴a∥b.
∠1=∠4(答案不唯一)
6. 如图Z7-7,∠A=70°,O是AB上一点,直线OD与AB所夹的∠BOD=78°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转_________.
8°
7.已知a,b,c为同一平面内三条不同直线,若a⊥b,c⊥b,则a与c的位置关系是_________.
8.如图Z7-8,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF,则下列结论正确的是_________(填序号).
①∠BAD+∠ADC=180°;
②AF∥DE;③∠DAF=∠F;
④若CD=DF,则DE=AF.
a∥c
①②③
9.如图Z7-9,已知AB∥CD,∠1=∠2,CF平分∠ECD.
(1)试判断直线AC与BD的位置关系,并说明理由;
(2)若∠1=80°,求∠3的度数.
解:(1)AC∥BD.理由如下.
∵AB∥CD,
∴∠2=∠CDF.
∵∠1=∠2,
∴∠1=∠CDF.
∴AC∥BD.
(2)∵∠1=80°,
∴∠ECD=180°-∠1=180°-80°=100°.
∵CF平分∠ECD,
∴∠ECF= ∠ECD= ×100°=50°.
∵AC∥BD,∴∠3=∠ECF=50°.
10.如图Z7-10,AD平分∠BAC,点E,F分别在边BC,AB上,且∠BFE=∠DAC,延长EF,CA交于点G.求证:∠G=∠AFG.
证明:∵AD平分∠BAC,
∴∠BAD=∠DAC.
∵∠BFE=∠DAC,
∴∠BFE=∠BAD.
∴EG∥AD.
∴∠G=∠DAC,∠AFG=∠FAD.
∴∠G=∠AFG.
11. 已知:如图Z7-11,∠A=∠ADE,∠C=∠E.
(1)若∠EDC=3∠C,求∠C的度数;
(2)求证:BE∥CD.
(1)解:∵∠A=∠ADE,
∴AC∥DE.
∴∠EDC+∠C=180°.
又∵∠EDC=3∠C,
∴4∠C=180°,即∠C=45°.
(2)证明:∵AC∥DE,
∴∠E=∠ABE.
又∵∠C=∠E,
∴∠C=∠ABE.
∴BE∥CD.
12.如图Z7-12,已知∠1+∠2=180°,∠B=∠3.求证:AB∥CD.
证明:∵∠1+∠2=180°,∠2+∠AFE=180°,
∴∠1=∠AFE.
∴BC∥DE.
∴∠AED=∠B.
又∵∠B=∠3,
∴∠AED=∠3.
∴AB∥CD.
13.如图Z7-13,已知∠EGB+∠CHE=180°,GM平分∠BGF,HN平分∠CHE.
(1)求证:AB∥CD;
(2)求证:∠M=∠N.
证明:(1)∵∠EGB+∠CHE=180°,∠CHE+∠EHD=180°,
∴∠EGB=∠EHD.
∴AB∥CD.
(2)∵AB∥CD,
∴∠BGF=∠CHE.
∵GM平分∠BGF,HN平分∠CHE,
∴∠NHE=∠MGF.
∴GM∥NH.
∴∠M=∠N.
专题3 三角形内角和定理及其推论
1.如图Z7-14,在△ABC中,∠B=∠C=65°,点D是BC边上任意一点,过点D作DF∥AB交AC于点E,则∠FEC的度数是( )
A. 120°
B. 130°
C. 145°
D.150°
B
2. (2020北京)如图Z7-15,AB和CD相交于点O,则下列结论正确的是( )
A. ∠1=∠2
B. ∠2=∠3
C. ∠1>∠4+∠5
D.∠2<∠5
A
3. (2020江西)如图Z7-16,∠1=∠2=65°,∠3=35°,则下列结论错误的是( )
A. AB∥CD
B. ∠B=30°
C. ∠C+∠2=∠EFC
D.CG>FG
C
4.如图Z7-17,CE是△ABC的外角∠ACD的平分线.若∠B=35°,∠ACE=60°,则∠A=( )
A.35°
B.95°
C.85°
D.75°
C
5.如图Z7-18,点D在BC的延长线上,DE⊥AB于点E,交AC于点F.若∠A=35°,∠D=15°,则∠ACB的度数为( )
A.65°
B.70°
C.75°
D.85°
B
6. (2020杭州)如图Z7-19,AB∥CD,EF分别与AB,CD交于点B,F.若∠E=30°,∠EFC=130°,则∠A=_________.
20°
7. 一副透明的三角板,如图Z7-20所示叠放,直角三角板的斜边AB,CE相交于点D,则∠BDC=_________.
75°
8.如图Z7-21,在△ABC中,∠B=56°,∠C=34°,AD为△ABC的角平分线,延长DA至点E,过点E作EH⊥BC,垂足为点H,则∠E=_________.
11°
9.如图Z7-22,在△ABC中,∠1= ∠ABC,∠2= ∠ACB,∠BDC=130°,求∠A的度数.
解:∵∠BDC=130°,
∴∠1+∠2=50°.
∵∠ABC=3∠1,
∠ACB=3∠2,
∴∠ABC+∠ACB=150°.
∴∠A=180°-∠ABC-∠ACB=30°.
10.如图Z7-23,点E在AC上,点F在AB上,BE与CF交于点O,且∠C=2∠B,∠BFC比∠BEC大20°.
(1)求∠C的度数;
(2)若∠A=70°,求∠BEC的度数.
解:(1)由三角形外角的性质可知,∠BFC=∠A+∠C,∠BEC=∠A+∠B.
由题意,得∠A+∠C=∠A+∠B+20°,且∠C=2∠B,
则∠C= ∠C+20°.
解得∠C=40°.
(2)由(1)得∠B= ∠C=20°,
∴∠BEC=∠A+∠B=90°.
11. 如图Z7-24,在△ABC中,∠BAC=90°,BD平分∠ABC,CD∥AB交BD于点D,已知∠D=29°,求∠1的度数.
解:∵CD∥AB,∠D=29°,
∴∠ABD=∠D=29°.
又∵BD平分∠ABC,
∴∠ABC=2∠ABD=58°.
∴∠1=180°-∠BAC-∠ABC
=180°-90°-58°
=32°.
12.如图Z7-25,在△ABC中,∠A=80°,∠B=30°,CD平分∠ACB,DE∥AC.
(1)求∠DEB的度数;
(2)求∠BDC的度数.
解:(1)在△ABC中,∠A=80°,∠B=30°,
∴∠ACB=180°-80°-30°=70°.
又∵DE∥AC,
∴∠DEB=∠ACB=70°.
(2)∵CD平分∠ACB,∠ACB=70°,
∴∠ACD=∠ECD= ∠ACB=35°.
∴∠BDC=180°-∠B-∠ECD
=180°-30°-35°
=115°.
13. 如图Z7-26,在△ABC中,点D在BC上,点E在AC上,AD交BE于点F.已知EG∥AD交BC于点G,EH⊥BE交BC于点H,∠HEG=50°.
(1)求∠BFD的度数;
(2)若∠BAD=∠EBC,∠C=41°,
求∠BAC的度数.
解:(1)∵EH⊥BE,
∴∠BEH=90°.
∵∠HEG=50°,
∴∠BEG=40°.
∵EG∥AD,
∴∠BFD=∠BEG=40°.
(2)∵∠BFD=∠BAD+∠ABE,∠BAD=∠EBC,
∴∠BFD=∠EBC+∠ABE=∠ABC=40°.
∵∠C=41°,
∴∠BAC=180°-∠ABC-∠C
=180°-40°-41°
=99°.
谢 谢
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
