23.3 课题学习 图案设计 同步练习(含答案)
文档属性
| 名称 | 23.3 课题学习 图案设计 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 362.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-19 16:35:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
23.3课题学习图案设计人教版初中数学九年级上册同步练习
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共10小题,共30.0分)
冰墩墩是深受大家喜爱的北京冬奥会吉祥物,它寓意创造非凡、探索未来.下列图形中可看作是由左侧“冰墩墩”图形平移后得到的图形是( )
A. B.
C. D.
把如图所示的“调皮”表情进行平移,能得到的图形是( )
A. B.
C. D.
如图所示的图案是一些汽车的车标,可以看作由“基本图案”经过平移得到的是( )
A. B.
C. D.
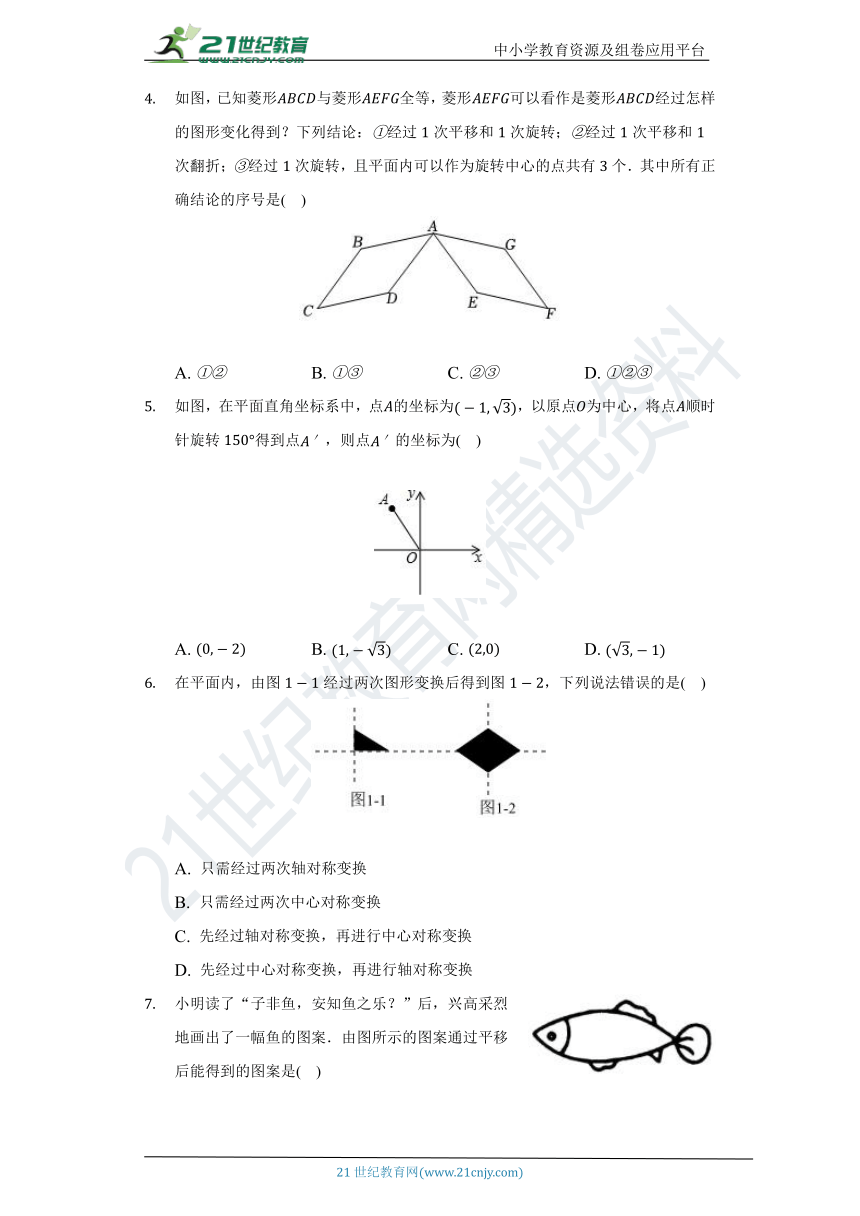
如图,已知菱形与菱形全等,菱形可以看作是菱形经过怎样的图形变化得到?下列结论:经过次平移和次旋转;经过次平移和次翻折;经过次旋转,且平面内可以作为旋转中心的点共有个.其中所有正确结论的序号是( )
A. B. C. D.
如图,在平面直角坐标系中,点的坐标为,以原点为中心,将点顺时针旋转得到点,则点的坐标为( )
A. B. C. D.
在平面内,由图经过两次图形变换后得到图,下列说法错误的是( )
A. 只需经过两次轴对称变换
B. 只需经过两次中心对称变换
C. 先经过轴对称变换,再进行中心对称变换
D. 先经过中心对称变换,再进行轴对称变换
小明读了“子非鱼,安知鱼之乐?”后,兴高采烈地画出了一幅鱼的图案.由图所示的图案通过平移后能得到的图案是( )
A. B.
C. D.
以下由两个等腰直角三角形组合成的图案中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
如图,是等腰直角三角形,是过点的直线,,,则通过下列变换能与重合的是( )
A. 绕点逆时针旋转度 B. 沿的垂直平分线翻折
C. 绕的中点顺时针旋转度 D. 沿方向平移
如图,在方格纸中,将绕点按顺时针方向旋转后得到,则下列四个图形中正确的是( )
A. B.
C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
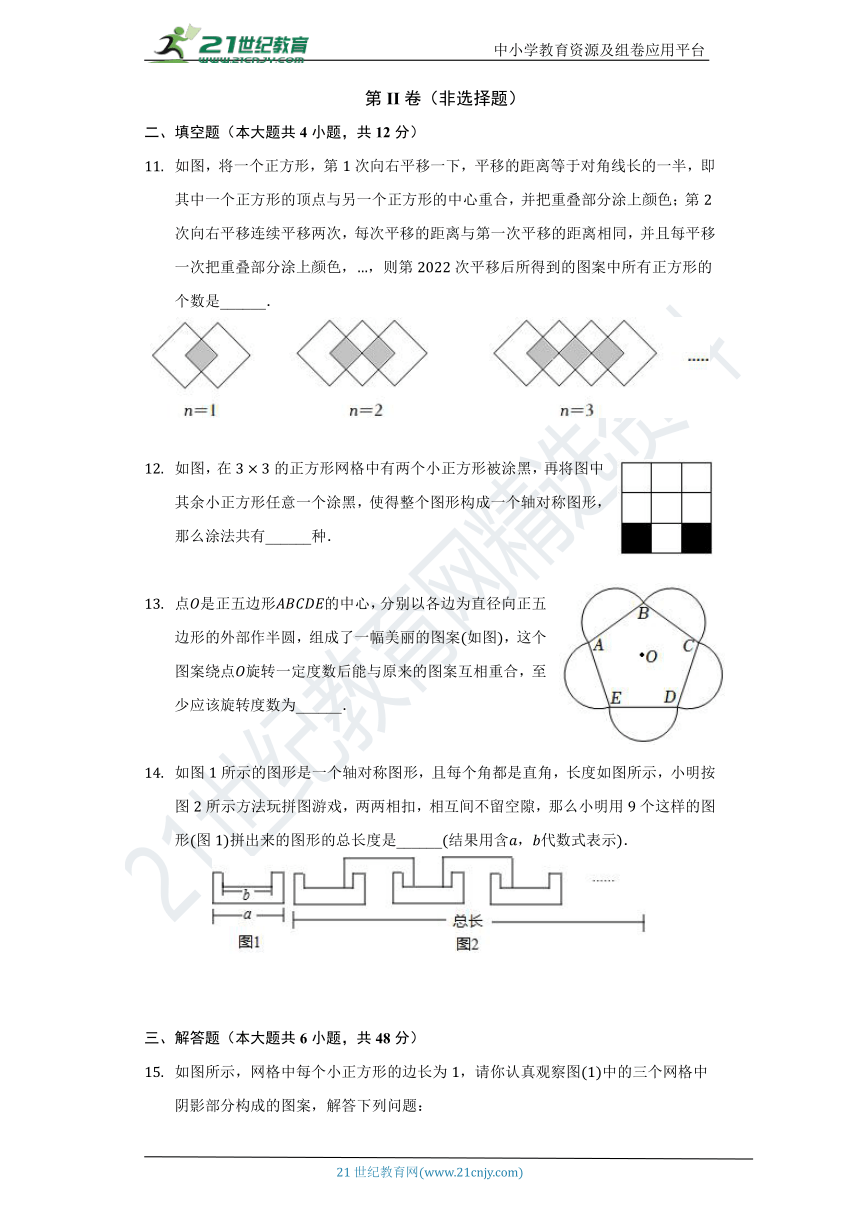
如图,将一个正方形,第次向右平移一下,平移的距离等于对角线长的一半,即其中一个正方形的顶点与另一个正方形的中心重合,并把重叠部分涂上颜色;第次向右平移连续平移两次,每次平移的距离与第一次平移的距离相同,并且每平移一次把重叠部分涂上颜色,,则第次平移后所得到的图案中所有正方形的个数是______.
如图,在的正方形网格中有两个小正方形被涂黑,再将图中其余小正方形任意一个涂黑,使得整个图形构成一个轴对称图形,那么涂法共有______种.
点是正五边形的中心,分别以各边为直径向正五边形的外部作半圆,组成了一幅美丽的图案如图,这个图案绕点旋转一定度数后能与原来的图案互相重合,至少应该旋转度数为______.
如图所示的图形是一个轴对称图形,且每个角都是直角,长度如图所示,小明按图所示方法玩拼图游戏,两两相扣,相互间不留空隙,那么小明用个这样的图形图拼出来的图形的总长度是______结果用含,代数式表示.
三、解答题(本大题共6小题,共48分)
如图所示,网格中每个小正方形的边长为,请你认真观察图中的三个网格中阴影部分构成的图案,解答下列问题:
这三个图案都具有以下共同特征:都是______对称图形,都不是______对称图形.
请在图中设计出一个面积为,且具备上述特征的图案,要求所画图案不能与图中所给出的图案相同.
如图,在平面直角坐标系中,的顶点都在网格点上,,,.
在网格中画出向下平移个单位,再向左平移个单位得到的图形;
在网格中画出绕原点顺时针旋转后的图形,并写出点的坐标.
如图,在中,,,点是边上一点,连接,将线段绕点逆时针旋转至,连接,,取的中点,连接.
求证:;
问与有何数量关系?写出你的结论并证明;
若点在上运动,则四边形能否形成平行四边形?若能,请直接写出此时的长;若不能,说明理由.
【基础回顾】如图,是正方形中边上任意一点,以点为中心,将顺时针旋转后得到,若连接,则的形状为______;
【类比探究】如图,在的条件下,设与相交于点,在上取点,使,连接,猜想与的数量关系,并给予证明;
【联想拓展】如图,在中,,点在上,求,,之间存在的数量关系.
如图,在平面直角坐标系中,三个顶点的坐标分别为,,.
画出关于原点成中心对称的;
画出绕点逆时针旋转所得到的;
将先向右平移个单位长度,再向上平移个单位长度,画出第二次平移后的.
若看成是由经过一次平移得到的,则这一平移的距离等于______个单位长度.
如图,方格纸中每个小正方形的边长都是个单位长度,在方格纸中建立如图所示的平面直角坐标系,的顶点都在格点上.
将向右平移个单位长度得到,请画出;
画出关于点的中心对称图形;
若将绕某一点旋转可得到,请直接写出旋转中心的坐标.
答案和解析
1.【答案】
【解析】解:根据“平移”的定义可知,由题图经过平移得到的图形是.
故选:.
根据平移的意义“平移是指在同一平面内,将一个图形整体按照某个直线方向移动一定的距离,这样的图形运动叫做图形的平移运动,简称平移”.
本题考查了生活中平移的现象,解决本题的关键是熟记平移的定义.
2.【答案】
【解析】解:根据平移定义可知:
把如图所示的“调皮”表情进行平移,能得到的图形是.
故选:.
在平面内,把一个图形整体沿某一的方向移动,这种图形的平行移动,叫做平移变换,简称平移.平移是指图形的
本题考查了生活中的平移现象,解决本题的关键是掌握平移定义.
3.【答案】
【解析】解:观察图形可知,图案可以看作由“基本图案”经过平移得到.
故选:.
根据平移的性质:不改变图形的形状和大小,不可旋转与翻转,将题中所示的图案通过平移后可以得到的图案是.
此题主要考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转,而导致错选.
4.【答案】
【解析】解:如图,先将菱形向右平移,再绕着点顺时针旋转得到菱形,故正确;
如图,将菱形先平移,再沿直线翻折可得菱形,故正确;
如图,经过次旋转,且平面内可以作为旋转中心的点有和,共有个,故不正确;
故选:.
依据旋转变换以及轴对称变换,分别画图可得结论.
本题主要考查了菱形的性质和几何变换,在轴对称变换下,对应线段相等,对应直线段或者平行,或者交于对称轴,且这两条直线的夹角被对称轴平分.在旋转变换下,对应线段相等,对应直线的夹角等于旋转角.
5.【答案】
【解析】解:如下图:作轴于点,延长至点,使,易知垂直平分线段,
,
点的坐标为,
,,,
在中,由勾股定理得:,
,
即是等边三角形,
,
将点顺时针旋转得到点后,如图所示,
,,
、,即,
故选:.
作轴于点,由、可得,从而知将点顺时针旋转得到点后如图所示,,,继而可得答案.
本题考查了坐标与图形的变化旋转,根据点的坐标求出,再根据旋转变换只改变图形的位置,不改变图形的形状与大小确定出点在上是解题的关键.
6.【答案】
【解析】解:、只需经过两次轴对称变换,能由图经过两次图形变换后得到图,故不符合题意;
B、只需经过两次中心对称变换,能由图经过两次图形变换后得到图,故不符合题意;
C、先经过轴对称变换,再进行中心对称变换不能由图经过两次图形变换后得到图,故符合题意;
D、先经过中心对称变换,再进行轴对称变换,能由图经过两次图形变换后得到图,故不符合题意;
故选:.
根据轴对称和中心对称的性质即可得到结论.
本题考查了几何变换的类型,轴对称和中心对称,熟练掌握轴对称和中心对称的图形的特征是解题的关键.
7.【答案】
【解析】解:根据平移不改变图形的形状、大小和方向,
将题图所示的图案通过平移后可以得到的图案是,
其它三项皆改变了方向,故错误.
故选:.
根据平移的定义和性质得出平移后的图案即可.
本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状、大小和方向,学生易混淆图形的平移与旋转或翻转.
8.【答案】
【解析】解:、不是中心对称图形,也不是轴对称图形.本选项不符合题意;
B、是轴对称图形,不是中心对称图形.本选项不符合题意;
C、是中心对称图形,不是轴对称图形.本选项不符合题意;
D、既是轴对称图形又是中心对称图形.本选项符合题意.
故选:.
根据轴对称图形,中心对称图形的定义判断即可.
本题考查利用旋转,轴对称设计图案,解题的关键是理解中心对称图形,轴对称图形的定义,属于中考常考题型.
9.【答案】
【解析】解:,,
,
又,
同角的余角相等,
在与中,
,
≌.
,.
A、绕点旋转后,与不重合,即与不重合,故选项A不符合题意;
B、与不关于的中垂线对称,则沿的中垂线翻折后不重合,故选项B不符合题意;
C、因为是等腰直角三角形,所以,所以绕中点逆时针旋转度,则与重合,故选项C符合题意;
D、先沿方向平移,使点与点重合后,再将平移后的三角形绕点逆时针旋转度,则与重合,故选项D不符合题意;
故选:.
根据全等三角形的判定定理得到≌,则,结合平移与旋转的性质进行判断.
本题考查了全等三角形的判定与性质,旋转与平移的性质.无论旋转还是平移,运动后的图形与原图形是全等的.
10.【答案】
【解析】解:选项是原图形的对称图形故不正确;
选项是绕点按顺时针方向旋转后得到,故B正确;
选项旋转后的形状发生了改变,故C不正确;
选项是按逆时针方向旋转,故D不正确;
故选:.
本题主要考查旋转的性质,旋转过程中图形和大小都不发生变化,根据旋转性质判断即可.
本题主要考查旋转的性质,熟练掌握并应用旋转的性质是解题的关键,重点注意旋转的方向和角度.
11.【答案】
【解析】解:第一次平移形成三个正方形,
第二次平移形成七个正方形,
第三次平移形成个正方形,
则分析这几次平移,得出规律,第次平移后所得到的图案中正方形的个数是.
当时,,
故答案为:
本题要根据平移的性质,和图示总结出规律,得出第次平移后所得到的图案中正方形的个数.
要根据平移的性质,根据前三次平移的情况,总结出规律,得出第次平移后所得到的图案中正方形的个数.
12.【答案】
【解析】解:如图所示:所标数字之处都可以构成轴对称图形,共有种情形,
故答案为:.
直接利用轴对称图形的性质分析得出答案.
此题主要考查了利用轴对称设计图案,正确掌握轴对称图形的性质是解题关键.
13.【答案】
【解析】解:连接,,则这个图形至少旋转才能与原图象重合,
.
故答案为:.
直接利用旋转图形的性质进而得出旋转角.
此题主要考查了旋转图形,正确掌握旋转图形的性质是解题关键.
14.【答案】
【解析】
【分析】
本题主要考查了利用轴对称设计图案和列代数式,利用轴对称设计图案关键是要熟悉轴对称的性质,属于较易题.
用个这样的图形的总长减去拼接时的重叠部分,即可得到拼出来的图形的总长度.
【解答】
解:由图可得,拼出来的图形的总长度.
故答案为:.
15.【答案】中心;轴
见解析.
【解析】解:中心、轴;
如图所示:
观察三个图形,利用中心对称和轴对称的性质即可解答;
根据中心对称的性质设计图案即可.
本题考查的是利用旋转设计图案,熟知图形旋转的性质是解答此题的关键.
16.【答案】解:如图,即为所求;
如图,即为所求.点的坐标.
【解析】利用平移变换的性质分别作出,,的对应点,,即可;
利用旋转变换的性质分别作出,,的对应点,,即可.
本题考查作图旋转变换,平移变换等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
17.【答案】证明:把绕点逆时针旋转得到线段,
,.
又,
,
在和中,
,
≌,
;
解:.
证明:延长到,使,交于点,
,,
,
≌,
,,
,
为的中点,
,
在的垂直平分线上,
又,
点在的垂直平分线上,
垂直平分,
,
在和中,
,
≌,
,
又,,
,
在和中,
,
≌,
,
又,
;
解:四边形能形成平行四边形.
,,
,
,
,
若,则四边形是平行四边形,
≌,
,
,
由知,,
,
,
.
【解析】由旋转的性质得出,证明≌,由全等三角形的性质得出;
延长到,使,交于点,证明≌,由全等三角形的性质得出,证明≌,由全等三角形的性质得出,则可得出结论;
证出,若,则四边形是平行四边形,由全等三角形的性质及可列出关于的方程,求出即可得出答案.
本题是几何变换综合题,主要考查了等腰直角三角形的性质,旋转的性质,平行四边形的性质,全等三角形的判定与性质,勾股定理等知识,证明≌是解题的关键.
18.【答案】等腰直角三角形
【解析】解:【基础回顾】四边形为正方形,
,,,
顺时针旋转,得,
,,
为等腰直角三角形;
故答案为:等腰直角三角形;
【类比探究】.
证明:将顺时针旋转后得到,
,,
,
≌,
.
【联想拓展】.
将逆时针旋转后得到,连接,则是等腰直角三角形,
由旋转的性质可知,,
,
,
,
,
,
.
【基础回顾】由正方形的性质得出,,,由旋转的性质得出,,则可得出结论;
【类比探究】证明≌,由全等三角形的性质可得出结论;
【联想拓展】将逆时针旋转后得到,连接,则是等腰直角三角形,由旋转的性质得出,,证出,由勾股定理可得出答案.
本题是几何变换综合题,考查了等腰直角三角形的判定与性质,勾股定理,旋转的性质,正方形的性质,熟练掌握旋转的性质是解题的关键.
19.【答案】
【解析】解:如图,即为所求;
如图,即为所求;
如图,即为所求;
,
看成是由经过一次平移得到的,这一平移的距离等于个单位长度.
故答案为:.
根据中心对称性质即可画出关于原点成中心对称的;
根据旋转的性质即可画出绕点逆时针旋转所得到的;
根据平移的性质即可将先向右平移个单位长度,再向上平移个单位长度,画出第二次平移后的进而可以解决问题.
本题考查了作图旋转变换,平移变换,解决本题的关键是掌握旋转的性质.
20.【答案】解:如图,即为所求;
如图,即为所求;
根据图形可知:
旋转中心的坐标为:.
【解析】本题考查了平移、中心对称、旋转作图,掌握相关的点的变换是解题关键.
根据平移的性质即可将向右平移个单位长度得到;
根据中心对称的定义即可画出关于点的中心对称图形;
根据旋转的性质即可将绕某一点旋转可得到,进而写出旋转中心的坐标.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
23.3课题学习图案设计人教版初中数学九年级上册同步练习
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共10小题,共30.0分)
冰墩墩是深受大家喜爱的北京冬奥会吉祥物,它寓意创造非凡、探索未来.下列图形中可看作是由左侧“冰墩墩”图形平移后得到的图形是( )
A. B.
C. D.
把如图所示的“调皮”表情进行平移,能得到的图形是( )
A. B.
C. D.
如图所示的图案是一些汽车的车标,可以看作由“基本图案”经过平移得到的是( )
A. B.
C. D.
如图,已知菱形与菱形全等,菱形可以看作是菱形经过怎样的图形变化得到?下列结论:经过次平移和次旋转;经过次平移和次翻折;经过次旋转,且平面内可以作为旋转中心的点共有个.其中所有正确结论的序号是( )
A. B. C. D.
如图,在平面直角坐标系中,点的坐标为,以原点为中心,将点顺时针旋转得到点,则点的坐标为( )
A. B. C. D.
在平面内,由图经过两次图形变换后得到图,下列说法错误的是( )
A. 只需经过两次轴对称变换
B. 只需经过两次中心对称变换
C. 先经过轴对称变换,再进行中心对称变换
D. 先经过中心对称变换,再进行轴对称变换
小明读了“子非鱼,安知鱼之乐?”后,兴高采烈地画出了一幅鱼的图案.由图所示的图案通过平移后能得到的图案是( )
A. B.
C. D.
以下由两个等腰直角三角形组合成的图案中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
如图,是等腰直角三角形,是过点的直线,,,则通过下列变换能与重合的是( )
A. 绕点逆时针旋转度 B. 沿的垂直平分线翻折
C. 绕的中点顺时针旋转度 D. 沿方向平移
如图,在方格纸中,将绕点按顺时针方向旋转后得到,则下列四个图形中正确的是( )
A. B.
C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
如图,将一个正方形,第次向右平移一下,平移的距离等于对角线长的一半,即其中一个正方形的顶点与另一个正方形的中心重合,并把重叠部分涂上颜色;第次向右平移连续平移两次,每次平移的距离与第一次平移的距离相同,并且每平移一次把重叠部分涂上颜色,,则第次平移后所得到的图案中所有正方形的个数是______.
如图,在的正方形网格中有两个小正方形被涂黑,再将图中其余小正方形任意一个涂黑,使得整个图形构成一个轴对称图形,那么涂法共有______种.
点是正五边形的中心,分别以各边为直径向正五边形的外部作半圆,组成了一幅美丽的图案如图,这个图案绕点旋转一定度数后能与原来的图案互相重合,至少应该旋转度数为______.
如图所示的图形是一个轴对称图形,且每个角都是直角,长度如图所示,小明按图所示方法玩拼图游戏,两两相扣,相互间不留空隙,那么小明用个这样的图形图拼出来的图形的总长度是______结果用含,代数式表示.
三、解答题(本大题共6小题,共48分)
如图所示,网格中每个小正方形的边长为,请你认真观察图中的三个网格中阴影部分构成的图案,解答下列问题:
这三个图案都具有以下共同特征:都是______对称图形,都不是______对称图形.
请在图中设计出一个面积为,且具备上述特征的图案,要求所画图案不能与图中所给出的图案相同.
如图,在平面直角坐标系中,的顶点都在网格点上,,,.
在网格中画出向下平移个单位,再向左平移个单位得到的图形;
在网格中画出绕原点顺时针旋转后的图形,并写出点的坐标.
如图,在中,,,点是边上一点,连接,将线段绕点逆时针旋转至,连接,,取的中点,连接.
求证:;
问与有何数量关系?写出你的结论并证明;
若点在上运动,则四边形能否形成平行四边形?若能,请直接写出此时的长;若不能,说明理由.
【基础回顾】如图,是正方形中边上任意一点,以点为中心,将顺时针旋转后得到,若连接,则的形状为______;
【类比探究】如图,在的条件下,设与相交于点,在上取点,使,连接,猜想与的数量关系,并给予证明;
【联想拓展】如图,在中,,点在上,求,,之间存在的数量关系.
如图,在平面直角坐标系中,三个顶点的坐标分别为,,.
画出关于原点成中心对称的;
画出绕点逆时针旋转所得到的;
将先向右平移个单位长度,再向上平移个单位长度,画出第二次平移后的.
若看成是由经过一次平移得到的,则这一平移的距离等于______个单位长度.
如图,方格纸中每个小正方形的边长都是个单位长度,在方格纸中建立如图所示的平面直角坐标系,的顶点都在格点上.
将向右平移个单位长度得到,请画出;
画出关于点的中心对称图形;
若将绕某一点旋转可得到,请直接写出旋转中心的坐标.
答案和解析
1.【答案】
【解析】解:根据“平移”的定义可知,由题图经过平移得到的图形是.
故选:.
根据平移的意义“平移是指在同一平面内,将一个图形整体按照某个直线方向移动一定的距离,这样的图形运动叫做图形的平移运动,简称平移”.
本题考查了生活中平移的现象,解决本题的关键是熟记平移的定义.
2.【答案】
【解析】解:根据平移定义可知:
把如图所示的“调皮”表情进行平移,能得到的图形是.
故选:.
在平面内,把一个图形整体沿某一的方向移动,这种图形的平行移动,叫做平移变换,简称平移.平移是指图形的
本题考查了生活中的平移现象,解决本题的关键是掌握平移定义.
3.【答案】
【解析】解:观察图形可知,图案可以看作由“基本图案”经过平移得到.
故选:.
根据平移的性质:不改变图形的形状和大小,不可旋转与翻转,将题中所示的图案通过平移后可以得到的图案是.
此题主要考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转,而导致错选.
4.【答案】
【解析】解:如图,先将菱形向右平移,再绕着点顺时针旋转得到菱形,故正确;
如图,将菱形先平移,再沿直线翻折可得菱形,故正确;
如图,经过次旋转,且平面内可以作为旋转中心的点有和,共有个,故不正确;
故选:.
依据旋转变换以及轴对称变换,分别画图可得结论.
本题主要考查了菱形的性质和几何变换,在轴对称变换下,对应线段相等,对应直线段或者平行,或者交于对称轴,且这两条直线的夹角被对称轴平分.在旋转变换下,对应线段相等,对应直线的夹角等于旋转角.
5.【答案】
【解析】解:如下图:作轴于点,延长至点,使,易知垂直平分线段,
,
点的坐标为,
,,,
在中,由勾股定理得:,
,
即是等边三角形,
,
将点顺时针旋转得到点后,如图所示,
,,
、,即,
故选:.
作轴于点,由、可得,从而知将点顺时针旋转得到点后如图所示,,,继而可得答案.
本题考查了坐标与图形的变化旋转,根据点的坐标求出,再根据旋转变换只改变图形的位置,不改变图形的形状与大小确定出点在上是解题的关键.
6.【答案】
【解析】解:、只需经过两次轴对称变换,能由图经过两次图形变换后得到图,故不符合题意;
B、只需经过两次中心对称变换,能由图经过两次图形变换后得到图,故不符合题意;
C、先经过轴对称变换,再进行中心对称变换不能由图经过两次图形变换后得到图,故符合题意;
D、先经过中心对称变换,再进行轴对称变换,能由图经过两次图形变换后得到图,故不符合题意;
故选:.
根据轴对称和中心对称的性质即可得到结论.
本题考查了几何变换的类型,轴对称和中心对称,熟练掌握轴对称和中心对称的图形的特征是解题的关键.
7.【答案】
【解析】解:根据平移不改变图形的形状、大小和方向,
将题图所示的图案通过平移后可以得到的图案是,
其它三项皆改变了方向,故错误.
故选:.
根据平移的定义和性质得出平移后的图案即可.
本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状、大小和方向,学生易混淆图形的平移与旋转或翻转.
8.【答案】
【解析】解:、不是中心对称图形,也不是轴对称图形.本选项不符合题意;
B、是轴对称图形,不是中心对称图形.本选项不符合题意;
C、是中心对称图形,不是轴对称图形.本选项不符合题意;
D、既是轴对称图形又是中心对称图形.本选项符合题意.
故选:.
根据轴对称图形,中心对称图形的定义判断即可.
本题考查利用旋转,轴对称设计图案,解题的关键是理解中心对称图形,轴对称图形的定义,属于中考常考题型.
9.【答案】
【解析】解:,,
,
又,
同角的余角相等,
在与中,
,
≌.
,.
A、绕点旋转后,与不重合,即与不重合,故选项A不符合题意;
B、与不关于的中垂线对称,则沿的中垂线翻折后不重合,故选项B不符合题意;
C、因为是等腰直角三角形,所以,所以绕中点逆时针旋转度,则与重合,故选项C符合题意;
D、先沿方向平移,使点与点重合后,再将平移后的三角形绕点逆时针旋转度,则与重合,故选项D不符合题意;
故选:.
根据全等三角形的判定定理得到≌,则,结合平移与旋转的性质进行判断.
本题考查了全等三角形的判定与性质,旋转与平移的性质.无论旋转还是平移,运动后的图形与原图形是全等的.
10.【答案】
【解析】解:选项是原图形的对称图形故不正确;
选项是绕点按顺时针方向旋转后得到,故B正确;
选项旋转后的形状发生了改变,故C不正确;
选项是按逆时针方向旋转,故D不正确;
故选:.
本题主要考查旋转的性质,旋转过程中图形和大小都不发生变化,根据旋转性质判断即可.
本题主要考查旋转的性质,熟练掌握并应用旋转的性质是解题的关键,重点注意旋转的方向和角度.
11.【答案】
【解析】解:第一次平移形成三个正方形,
第二次平移形成七个正方形,
第三次平移形成个正方形,
则分析这几次平移,得出规律,第次平移后所得到的图案中正方形的个数是.
当时,,
故答案为:
本题要根据平移的性质,和图示总结出规律,得出第次平移后所得到的图案中正方形的个数.
要根据平移的性质,根据前三次平移的情况,总结出规律,得出第次平移后所得到的图案中正方形的个数.
12.【答案】
【解析】解:如图所示:所标数字之处都可以构成轴对称图形,共有种情形,
故答案为:.
直接利用轴对称图形的性质分析得出答案.
此题主要考查了利用轴对称设计图案,正确掌握轴对称图形的性质是解题关键.
13.【答案】
【解析】解:连接,,则这个图形至少旋转才能与原图象重合,
.
故答案为:.
直接利用旋转图形的性质进而得出旋转角.
此题主要考查了旋转图形,正确掌握旋转图形的性质是解题关键.
14.【答案】
【解析】
【分析】
本题主要考查了利用轴对称设计图案和列代数式,利用轴对称设计图案关键是要熟悉轴对称的性质,属于较易题.
用个这样的图形的总长减去拼接时的重叠部分,即可得到拼出来的图形的总长度.
【解答】
解:由图可得,拼出来的图形的总长度.
故答案为:.
15.【答案】中心;轴
见解析.
【解析】解:中心、轴;
如图所示:
观察三个图形,利用中心对称和轴对称的性质即可解答;
根据中心对称的性质设计图案即可.
本题考查的是利用旋转设计图案,熟知图形旋转的性质是解答此题的关键.
16.【答案】解:如图,即为所求;
如图,即为所求.点的坐标.
【解析】利用平移变换的性质分别作出,,的对应点,,即可;
利用旋转变换的性质分别作出,,的对应点,,即可.
本题考查作图旋转变换,平移变换等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
17.【答案】证明:把绕点逆时针旋转得到线段,
,.
又,
,
在和中,
,
≌,
;
解:.
证明:延长到,使,交于点,
,,
,
≌,
,,
,
为的中点,
,
在的垂直平分线上,
又,
点在的垂直平分线上,
垂直平分,
,
在和中,
,
≌,
,
又,,
,
在和中,
,
≌,
,
又,
;
解:四边形能形成平行四边形.
,,
,
,
,
若,则四边形是平行四边形,
≌,
,
,
由知,,
,
,
.
【解析】由旋转的性质得出,证明≌,由全等三角形的性质得出;
延长到,使,交于点,证明≌,由全等三角形的性质得出,证明≌,由全等三角形的性质得出,则可得出结论;
证出,若,则四边形是平行四边形,由全等三角形的性质及可列出关于的方程,求出即可得出答案.
本题是几何变换综合题,主要考查了等腰直角三角形的性质,旋转的性质,平行四边形的性质,全等三角形的判定与性质,勾股定理等知识,证明≌是解题的关键.
18.【答案】等腰直角三角形
【解析】解:【基础回顾】四边形为正方形,
,,,
顺时针旋转,得,
,,
为等腰直角三角形;
故答案为:等腰直角三角形;
【类比探究】.
证明:将顺时针旋转后得到,
,,
,
≌,
.
【联想拓展】.
将逆时针旋转后得到,连接,则是等腰直角三角形,
由旋转的性质可知,,
,
,
,
,
,
.
【基础回顾】由正方形的性质得出,,,由旋转的性质得出,,则可得出结论;
【类比探究】证明≌,由全等三角形的性质可得出结论;
【联想拓展】将逆时针旋转后得到,连接,则是等腰直角三角形,由旋转的性质得出,,证出,由勾股定理可得出答案.
本题是几何变换综合题,考查了等腰直角三角形的判定与性质,勾股定理,旋转的性质,正方形的性质,熟练掌握旋转的性质是解题的关键.
19.【答案】
【解析】解:如图,即为所求;
如图,即为所求;
如图,即为所求;
,
看成是由经过一次平移得到的,这一平移的距离等于个单位长度.
故答案为:.
根据中心对称性质即可画出关于原点成中心对称的;
根据旋转的性质即可画出绕点逆时针旋转所得到的;
根据平移的性质即可将先向右平移个单位长度,再向上平移个单位长度,画出第二次平移后的进而可以解决问题.
本题考查了作图旋转变换,平移变换,解决本题的关键是掌握旋转的性质.
20.【答案】解:如图,即为所求;
如图,即为所求;
根据图形可知:
旋转中心的坐标为:.
【解析】本题考查了平移、中心对称、旋转作图,掌握相关的点的变换是解题关键.
根据平移的性质即可将向右平移个单位长度得到;
根据中心对称的定义即可画出关于点的中心对称图形;
根据旋转的性质即可将绕某一点旋转可得到,进而写出旋转中心的坐标.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
