【专题讲义】人教A版必修1 专题08 指数与指数函数(解析版)
文档属性
| 名称 | 【专题讲义】人教A版必修1 专题08 指数与指数函数(解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-19 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
专题08 指数与指数函数
【考点总结】
1.根式
(1)根式的概念
①若xn=a,则x叫做a的n次方根,其中n>1且n∈N*.式子叫做根式,这里n叫做根指数,a叫做被开方数.www.21-cn-jy.com
②a的n次方根的表示:
xn=a
(2)根式的性质
①()n=a(n∈N*,且n>1);
②=
2.有理数指数幂
(1)幂的有关概念
①正分数指数幂:a=(a>0,m,n∈N*,且n>1);
②负分数指数幂:a-==(a>0,m,n∈N*,且n>1);
③0的正分数指数幂等于0,0的负分数指数幂无意义.
(2)有理数指数幂的运算性质
①aras=ar+s(a>0,r,s∈Q);
②(ar)s=ars(a>0,r,s∈Q);
③(ab)r=arbr(a>0,b>0,r∈Q).
3.指数函数的图象与性质
y=ax (a>0且a≠1) a>1 0图象
定义域 R
值域 (0,+∞)
性质 过定点(0,1)
当x>0时,y>1;当x<0时,00时,01
在R上是增函数 在R上是减函数
【常用结论】
1.指数函数图象的画法
画指数函数y=ax(a>0,且a≠1)的图象,应抓住三个关键点:(1,a),(0,1),.
2.
指数函数的图象与底数大小的比较
如图是指数函数(1)y=ax, ( http: / / www.21cnjy.com )(2)y=bx,(3)y=cx,(4)y=dx的图象,底数a,b,c,d与1之间的大小关系为c>d>1>a>b>0.由此我们可得到以下规律:在第一象限内,指数函数y=ax(a>0,a≠1)的图象越高,底数越大.21世纪教育网版权所有
3.指数函数y=ax(a>0,且a≠1)的图象和性质跟a的取值有关,要特别注意应分a>1与0【易错总结】
(1)忽略n的范围导致式子(a∈R)化简出错;
(2)不能正确理解指数函数的概念致错;
(3)指数函数问题时刻注意底数的两种情况;
(4)复合函数问题容易忽略指数函数的值域致错.
例1.计算+=________.
解析:+=(1+)+(-1)=2.
答案:2
例2.若函数f(x)=(a2-3)·ax为指数函数,则a=________.
解析:由题意知即a=2.
答案:2
例3.若函数f(x)=ax在[-1,1]上的最大值为2,则a=________.
解析:当a>1时,a=2;当0即a=.
答案:2或
例4.函数y=2的值域为________.
解析:因为≠0,
所以2>0且2≠1.
答案:(0,1)∪(1,+∞)
【考点解析】
【考点】一、指数幂的化简与求值
例1.化简·(a>0,b>0)=________.
解析:原式=2×=21+3×10-1=.
答案:
例2.计算:+0.002--10(-2)-1+π0=________.
解析:原式=+500-+1=+10-10-20+1=-.
答案:-
例3.化简:÷×=________(a>0).
解析:原式=÷×=a(a-2b)××=a2.
答案:a2
指数幂运算的一般原则
(1)有括号的先算括号里的,无括号的先算指数运算.
(2)先乘除后加减,负指数幂化成正指数幂的倒数.
(3)底数是小数,先化成分数;底数是带分数的,先化成假分数.
(4)若是根式,应化为分数指数幂,尽可能用幂的形式表示,运用指数幂的运算性质来解答.
[提醒] 运算结果不能同时含有根号和分数指数幂,也不能既有分母又含有负指数,形式力求统一.
【考点】二、指数函数的图象及应用
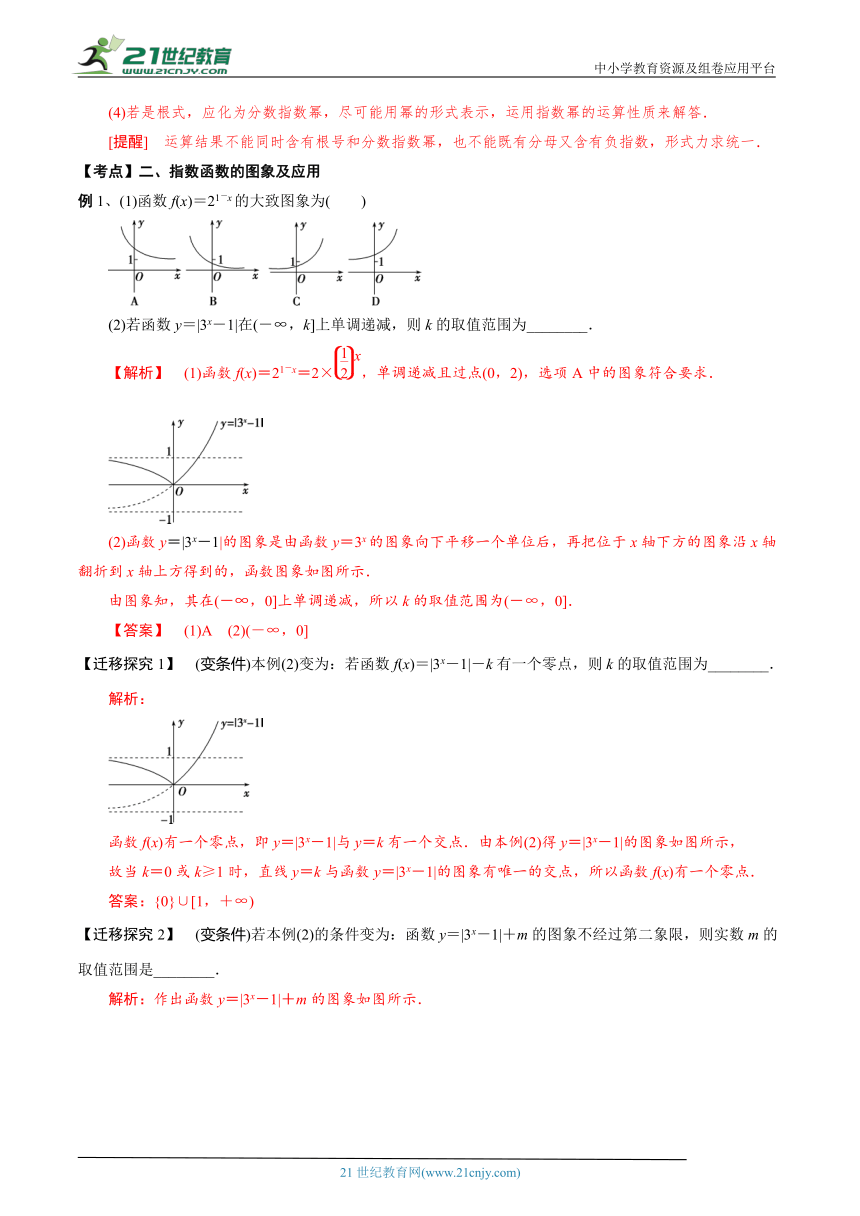
例1、(1)函数f(x)=21-x的大致图象为( )
(2)若函数y=|3x-1|在(-∞,k]上单调递减,则k的取值范围为________.
【解析】 (1)函数f(x)=21-x=2×,单调递减且过点(0,2),选项A中的图象符合要求.
(2)函数y=|3x-1 ( http: / / www.21cnjy.com )|的图象是由函数y=3x的图象向下平移一个单位后,再把位于x轴下方的图象沿x轴翻折到x轴上方得到的,函数图象如图所示.21cnjy.com
由图象知,其在(-∞,0]上单调递减,所以k的取值范围为(-∞,0].
【答案】 (1)A (2)(-∞,0]
【迁移探究1】 (变条件)本例(2)变为:若函数f(x)=|3x-1|-k有一个零点,则k的取值范围为________.
解析:
函数f(x)有一个零点,即y=|3x-1|与y=k有一个交点.由本例(2)得y=|3x-1|的图象如图所示,
故当k=0或k≥1时,直线y=k与函数y=|3x-1|的图象有唯一的交点,所以函数f(x)有一个零点.
答案:{0}∪[1,+∞)
【迁移探究2】 (变条件)若本例(2)的条件变为:函数y=|3x-1|+m的图象不经过第二象限,则实数m的取值范围是________.21教育网
解析:作出函数y=|3x-1|+m的图象如图所示.
由图象知m≤-1,即m∈(-∞,-1].
答案:(-∞,-1]
应用指数函数图象的4个技巧
(1)画指数函数y=ax(a>0,且a≠1)的图象,应抓住三个关键点:(1,a),(0,1),.
(2)已知函数解析式判断其图象一般是取特殊点,判断所给的图象是否过这些点,若不满足则排除.
(3)对于有关指数型函数的图象问题,一般是从 ( http: / / www.21cnjy.com )最基本的指数函数的图象入手,通过平移、伸缩、对称变换而得到.特别地,当底数a与1的大小关系不确定时应注意分类讨论.21·cn·jy·com
(4)有关指数方程、不等式问题的求解,往往利用相应的指数型函数图象,数形结合求解.
【变式】1.函数f(x)=ax-b的图象如图所示,其中a,b为常数,则下列结论正确的是( )
A.a>1,b<0 B.a>1,b>0
C.00 D.0解析:选D.由f(x)=ax-b ( http: / / www.21cnjy.com )的图象可以观察出函数f(x)=ax-b在定义域上单调递减,所以0【变式】2.若关于x的方程|ax-1|=2a(a>0,且a≠1)有两个不等实根,则a的取值范围是________.
解析:方程|ax-1|=2a(a>0,且a≠1)有两个不等实根转化为函数y=|ax-1|与y=2a有两个交点.
(1)当0<a<1时,如图①,所以0<2a<1,即
0<a<;
(2)当a>1时,如图②,而y=2a>1不符合要求.
所以0<a<.
答案:
【考点】三、指数函数的性质及应用
角度一 指数函数单调性的应用
例1、(1)已知a=2,b=4,c=25,则( )
A.bC.b(2)若f(x)=ex-ae-x为奇函数,则满足f(x-1)>-e2的x的取值范围是( )
A.(-2,+∞) B.(-1,+∞)
C.(2,+∞) D.(3,+∞)
【解析】 (1)因为a=2,b=4=2,由函数y=2x在R上为增函数知,b(2)由f(x)=ex-ae-x ( http: / / www.21cnjy.com )为奇函数,得f(-x)=-f(x),即e-x-aex=ae-x-ex,得a=1,所以f(x)=ex-e-x,则f(x)在R上单调递增,又f(x-1)>-e2=f(-2),所以x-1>-2,解得x>-1,故选B.
【答案】 (1)A (2)B
角度二 指数型复合函数的单调性
例2、(1)函数f(x)=的单调递减区间为________.
(2)已知函数f(x)=2|2x-m|(m为常数),若f(x)在区间[2,+∞)上是增函数,则m的取值范围是________.
【解析】 (1)设u=-x2+2x+1,
因为y=在R上为减函数,
所以函数f(x)=的减区间即为函数u=-x2+2x+1的增区间.
又u=-x2+2x+1的增区间为(-∞,1],
所以f(x)的减区间为(-∞,1].
(2)令t=|2x-m|,则t=| ( http: / / www.21cnjy.com )2x-m|在区间上单调递增,在区间上单调递减.而y=2t为R上的增函数,所以要使函数f(x)=2|2x-m|在[2,+∞)上单调递增,则有≤2,即m≤4,所以m的取值范围是(-∞,4].21·世纪*教育网
【答案】 (1)(-∞,1] (2)(-∞,4]
角度三 指数函数性质的综合问题
例3、已知函数f(x)=.
(1)若f(x)有最大值3,求a的值;
(2)若f(x)的值域是(0,+∞),求a的值.
【解】 (1)令g(x)=ax2-4x+3,f(x)=,
由于f(x)有最大值3,
所以g(x)应有最小值-1,
因此必有解得a=1,
即当f(x)有最大值3时,a的值等于1.
(2)令g(x)=ax2-4x+3,f(x)=,
由指数函数的性质知,
要使y=的值域为(0,+∞).
应使g(x)=ax2-4x+3的值域为R,
因此只能a=0.(因为若a≠0,则g(x)为二次函数,其值域不可能为R)
故f(x)的值域为(0,+∞)时,a的值为0.
(1)利用指数函数的性质比较大小或解不等式,最重要的是“同底”原则.
(2)求解与指数函数有关的复合函数问题,要明确复合函数的构成,涉及值域、单调区间、最值等问题时,都要借助“同增异减”这一性质分析判断. www-2-1-cnjy-com
【变式】1.设a=0.60.6,b=0.61.5,c=1.50.6,则a,b,c的大小关系是 ( )2-1-c-n-j-y
A.a<b<c B.a<c<b
C.b<a<c D.b<c<a
解析:选C.因为指数函数y=0.6x在(-∞,+∞)上为减函数,
所以0.60.6>0.61.5,即a>b,
又0<0.60.6<1,1.50.6>1,
所以a<c,
故选C.
【变式】2.若偶函数f(x)满足f(x)=2x-4(x≥0),则不等式f(x-2)>0的解集为________.
解析:因为f(x)为偶函数,
当x<0时,-x>0,则f(x)=f(-x)=2-x-4.
所以f(x)=
当f(x-2)>0时,有或
解得x>4或x<0.
所以不等式的解集为{x|x>4或x<0}.
答案:{x|x>4或x<0}
【变式】3.已知函数f(x)=(a>0且a≠1).
(1)求f(x)的定义域和值域;
(2)讨论f(x)的奇偶性;
(3)讨论f(x)的单调性.
解:(1)f(x)的定义域是R,令y=,得ax=-,因为≠1在定义域内恒成立,所以y≠1.
因为ax>0,所以->0,
解得-1所以f(x)的值域为(-1,1).
(2)因为f(-x)===-f(x),
所以f(x)是奇函数.
(3)f(x)==1-.
设x1,x2是R上任意两个实数,且x1则f(x1)-f(x2)=-
=.
因为x1所以当a>1时,a x2>ax1>0,
从而ax1+1>0,a x2+1>0,ax1-a x2<0,
所以f(x1)-f(x2)<0,即f(x1)当0a x2>0,
从而ax1+1>0,a x2+1>0,ax1-a x2>0,
所以f(x1)-f(x2)>0,即f(x1)>f(x2),f(x)为R上的减函数.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专题08 指数与指数函数
【考点总结】
1.根式
(1)根式的概念
①若xn=a,则x叫做a的n次方根,其中n>1且n∈N*.式子叫做根式,这里n叫做根指数,a叫做被开方数.www.21-cn-jy.com
②a的n次方根的表示:
xn=a
(2)根式的性质
①()n=a(n∈N*,且n>1);
②=
2.有理数指数幂
(1)幂的有关概念
①正分数指数幂:a=(a>0,m,n∈N*,且n>1);
②负分数指数幂:a-==(a>0,m,n∈N*,且n>1);
③0的正分数指数幂等于0,0的负分数指数幂无意义.
(2)有理数指数幂的运算性质
①aras=ar+s(a>0,r,s∈Q);
②(ar)s=ars(a>0,r,s∈Q);
③(ab)r=arbr(a>0,b>0,r∈Q).
3.指数函数的图象与性质
y=ax (a>0且a≠1) a>1 0
定义域 R
值域 (0,+∞)
性质 过定点(0,1)
当x>0时,y>1;当x<0时,0
在R上是增函数 在R上是减函数
【常用结论】
1.指数函数图象的画法
画指数函数y=ax(a>0,且a≠1)的图象,应抓住三个关键点:(1,a),(0,1),.
2.
指数函数的图象与底数大小的比较
如图是指数函数(1)y=ax, ( http: / / www.21cnjy.com )(2)y=bx,(3)y=cx,(4)y=dx的图象,底数a,b,c,d与1之间的大小关系为c>d>1>a>b>0.由此我们可得到以下规律:在第一象限内,指数函数y=ax(a>0,a≠1)的图象越高,底数越大.21世纪教育网版权所有
3.指数函数y=ax(a>0,且a≠1)的图象和性质跟a的取值有关,要特别注意应分a>1与0
(1)忽略n的范围导致式子(a∈R)化简出错;
(2)不能正确理解指数函数的概念致错;
(3)指数函数问题时刻注意底数的两种情况;
(4)复合函数问题容易忽略指数函数的值域致错.
例1.计算+=________.
解析:+=(1+)+(-1)=2.
答案:2
例2.若函数f(x)=(a2-3)·ax为指数函数,则a=________.
解析:由题意知即a=2.
答案:2
例3.若函数f(x)=ax在[-1,1]上的最大值为2,则a=________.
解析:当a>1时,a=2;当0
答案:2或
例4.函数y=2的值域为________.
解析:因为≠0,
所以2>0且2≠1.
答案:(0,1)∪(1,+∞)
【考点解析】
【考点】一、指数幂的化简与求值
例1.化简·(a>0,b>0)=________.
解析:原式=2×=21+3×10-1=.
答案:
例2.计算:+0.002--10(-2)-1+π0=________.
解析:原式=+500-+1=+10-10-20+1=-.
答案:-
例3.化简:÷×=________(a>0).
解析:原式=÷×=a(a-2b)××=a2.
答案:a2
指数幂运算的一般原则
(1)有括号的先算括号里的,无括号的先算指数运算.
(2)先乘除后加减,负指数幂化成正指数幂的倒数.
(3)底数是小数,先化成分数;底数是带分数的,先化成假分数.
(4)若是根式,应化为分数指数幂,尽可能用幂的形式表示,运用指数幂的运算性质来解答.
[提醒] 运算结果不能同时含有根号和分数指数幂,也不能既有分母又含有负指数,形式力求统一.
【考点】二、指数函数的图象及应用
例1、(1)函数f(x)=21-x的大致图象为( )
(2)若函数y=|3x-1|在(-∞,k]上单调递减,则k的取值范围为________.
【解析】 (1)函数f(x)=21-x=2×,单调递减且过点(0,2),选项A中的图象符合要求.
(2)函数y=|3x-1 ( http: / / www.21cnjy.com )|的图象是由函数y=3x的图象向下平移一个单位后,再把位于x轴下方的图象沿x轴翻折到x轴上方得到的,函数图象如图所示.21cnjy.com
由图象知,其在(-∞,0]上单调递减,所以k的取值范围为(-∞,0].
【答案】 (1)A (2)(-∞,0]
【迁移探究1】 (变条件)本例(2)变为:若函数f(x)=|3x-1|-k有一个零点,则k的取值范围为________.
解析:
函数f(x)有一个零点,即y=|3x-1|与y=k有一个交点.由本例(2)得y=|3x-1|的图象如图所示,
故当k=0或k≥1时,直线y=k与函数y=|3x-1|的图象有唯一的交点,所以函数f(x)有一个零点.
答案:{0}∪[1,+∞)
【迁移探究2】 (变条件)若本例(2)的条件变为:函数y=|3x-1|+m的图象不经过第二象限,则实数m的取值范围是________.21教育网
解析:作出函数y=|3x-1|+m的图象如图所示.
由图象知m≤-1,即m∈(-∞,-1].
答案:(-∞,-1]
应用指数函数图象的4个技巧
(1)画指数函数y=ax(a>0,且a≠1)的图象,应抓住三个关键点:(1,a),(0,1),.
(2)已知函数解析式判断其图象一般是取特殊点,判断所给的图象是否过这些点,若不满足则排除.
(3)对于有关指数型函数的图象问题,一般是从 ( http: / / www.21cnjy.com )最基本的指数函数的图象入手,通过平移、伸缩、对称变换而得到.特别地,当底数a与1的大小关系不确定时应注意分类讨论.21·cn·jy·com
(4)有关指数方程、不等式问题的求解,往往利用相应的指数型函数图象,数形结合求解.
【变式】1.函数f(x)=ax-b的图象如图所示,其中a,b为常数,则下列结论正确的是( )
A.a>1,b<0 B.a>1,b>0
C.0
解析:方程|ax-1|=2a(a>0,且a≠1)有两个不等实根转化为函数y=|ax-1|与y=2a有两个交点.
(1)当0<a<1时,如图①,所以0<2a<1,即
0<a<;
(2)当a>1时,如图②,而y=2a>1不符合要求.
所以0<a<.
答案:
【考点】三、指数函数的性质及应用
角度一 指数函数单调性的应用
例1、(1)已知a=2,b=4,c=25,则( )
A.b
A.(-2,+∞) B.(-1,+∞)
C.(2,+∞) D.(3,+∞)
【解析】 (1)因为a=2,b=4=2,由函数y=2x在R上为增函数知,b
【答案】 (1)A (2)B
角度二 指数型复合函数的单调性
例2、(1)函数f(x)=的单调递减区间为________.
(2)已知函数f(x)=2|2x-m|(m为常数),若f(x)在区间[2,+∞)上是增函数,则m的取值范围是________.
【解析】 (1)设u=-x2+2x+1,
因为y=在R上为减函数,
所以函数f(x)=的减区间即为函数u=-x2+2x+1的增区间.
又u=-x2+2x+1的增区间为(-∞,1],
所以f(x)的减区间为(-∞,1].
(2)令t=|2x-m|,则t=| ( http: / / www.21cnjy.com )2x-m|在区间上单调递增,在区间上单调递减.而y=2t为R上的增函数,所以要使函数f(x)=2|2x-m|在[2,+∞)上单调递增,则有≤2,即m≤4,所以m的取值范围是(-∞,4].21·世纪*教育网
【答案】 (1)(-∞,1] (2)(-∞,4]
角度三 指数函数性质的综合问题
例3、已知函数f(x)=.
(1)若f(x)有最大值3,求a的值;
(2)若f(x)的值域是(0,+∞),求a的值.
【解】 (1)令g(x)=ax2-4x+3,f(x)=,
由于f(x)有最大值3,
所以g(x)应有最小值-1,
因此必有解得a=1,
即当f(x)有最大值3时,a的值等于1.
(2)令g(x)=ax2-4x+3,f(x)=,
由指数函数的性质知,
要使y=的值域为(0,+∞).
应使g(x)=ax2-4x+3的值域为R,
因此只能a=0.(因为若a≠0,则g(x)为二次函数,其值域不可能为R)
故f(x)的值域为(0,+∞)时,a的值为0.
(1)利用指数函数的性质比较大小或解不等式,最重要的是“同底”原则.
(2)求解与指数函数有关的复合函数问题,要明确复合函数的构成,涉及值域、单调区间、最值等问题时,都要借助“同增异减”这一性质分析判断. www-2-1-cnjy-com
【变式】1.设a=0.60.6,b=0.61.5,c=1.50.6,则a,b,c的大小关系是 ( )2-1-c-n-j-y
A.a<b<c B.a<c<b
C.b<a<c D.b<c<a
解析:选C.因为指数函数y=0.6x在(-∞,+∞)上为减函数,
所以0.60.6>0.61.5,即a>b,
又0<0.60.6<1,1.50.6>1,
所以a<c,
故选C.
【变式】2.若偶函数f(x)满足f(x)=2x-4(x≥0),则不等式f(x-2)>0的解集为________.
解析:因为f(x)为偶函数,
当x<0时,-x>0,则f(x)=f(-x)=2-x-4.
所以f(x)=
当f(x-2)>0时,有或
解得x>4或x<0.
所以不等式的解集为{x|x>4或x<0}.
答案:{x|x>4或x<0}
【变式】3.已知函数f(x)=(a>0且a≠1).
(1)求f(x)的定义域和值域;
(2)讨论f(x)的奇偶性;
(3)讨论f(x)的单调性.
解:(1)f(x)的定义域是R,令y=,得ax=-,因为≠1在定义域内恒成立,所以y≠1.
因为ax>0,所以->0,
解得-1
(2)因为f(-x)===-f(x),
所以f(x)是奇函数.
(3)f(x)==1-.
设x1,x2是R上任意两个实数,且x1
=.
因为x1
从而ax1+1>0,a x2+1>0,ax1-a x2<0,
所以f(x1)-f(x2)<0,即f(x1)
从而ax1+1>0,a x2+1>0,ax1-a x2>0,
所以f(x1)-f(x2)>0,即f(x1)>f(x2),f(x)为R上的减函数.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
