湘教版数学八年级上册同步课件:2.5 第4课时 全等三角形的判定3——“AAS”(共12张PPT)
文档属性
| 名称 | 湘教版数学八年级上册同步课件:2.5 第4课时 全等三角形的判定3——“AAS”(共12张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 403.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-19 15:46:18 | ||
图片预览




文档简介
(共12张PPT)
第二章 三角形
2.5 第4课时 全等三角形的判定3——“AAS”
情景引入
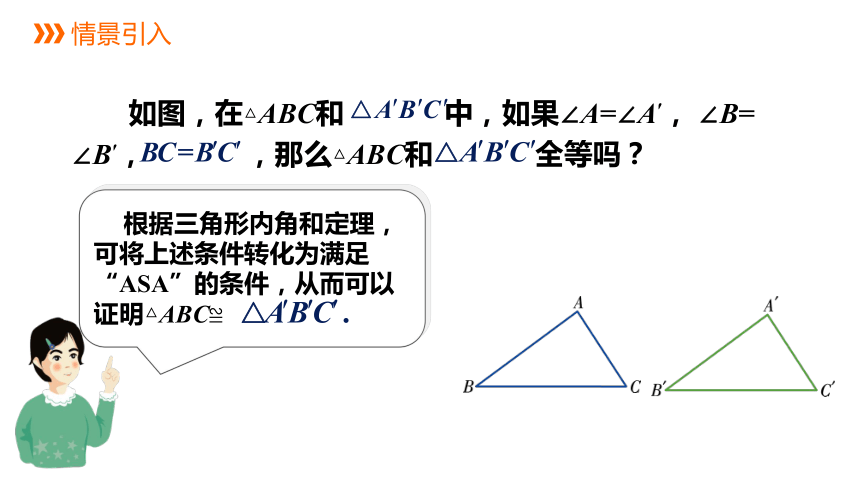
如图,在△ABC和 中,如果∠A=∠A′, ∠B= ∠B′, ,那么△ABC和 全等吗?
根据三角形内角和定理,可将上述条件转化为满足“ASA”的条件,从而可以证明△ABC≌
在△ABC和 中,
∵ ∠A = ∠A′,∠B = ∠B′,
∴ ∠C =∠C′.
又∵ ,∠B=∠B′,
∴ (ASA).
由此得到判定两个三角形全等的定理:
两角分别相等且其中一组等角的对边相等的两个三角形全等.
通常可简写成“角角边”或“AAS”.
获取新知
例1 已知:如图,∠B=∠D,∠1=∠2,求证:△ABC≌△ADC.
证明 ∵∠1 =∠2,
∴∠ACB=∠ACD(同角的补角相等).
在△ABC和△ADC中,
∴ △ABC≌△ADC (AAS).
∠B =∠D,
∠ACB =∠ACD,
AC = AC,
例题讲解
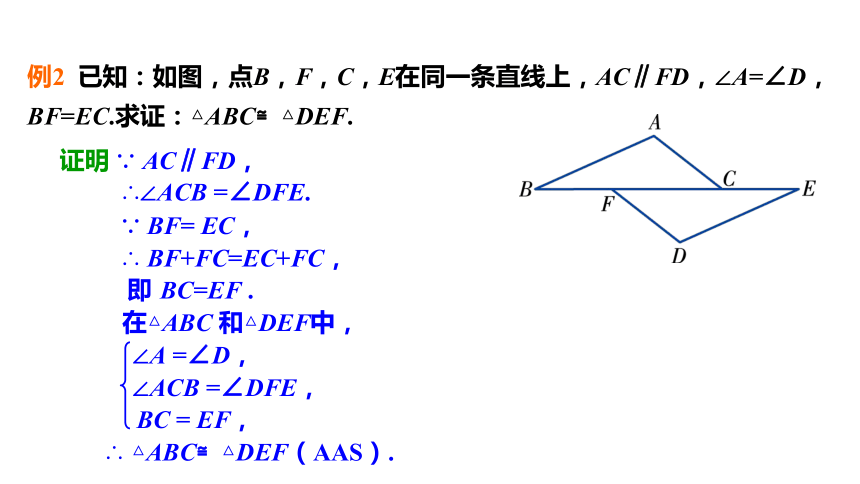
例2 已知:如图,点B,F,C,E在同一条直线上,AC∥FD,∠A=∠D,BF=EC.求证:△ABC≌△DEF.
证明 ∵ AC∥FD,
∴∠ACB =∠DFE.
∵ BF= EC,
∴ BF+FC=EC+FC,
即 BC=EF .
在△ABC 和△DEF中,
∴ △ABC≌△DEF(AAS).
∠A =∠D,
∠ACB =∠DFE,
BC = EF,
1. 已知:如图,∠1=∠2,AD=AE. 求证:△ADC≌△AEB.
∴ △ADC≌△AEB(AAS).
∠1 =∠2,
∠A =∠ A,
AD = AE,
证明
∵ 在△ADC 和△AEB中,
随堂演练
2. 已知:在△ABC中,∠ABC =∠ACB,BD⊥AC于点D,CE⊥AB于点E. 求证:BD=CE.
证明 由题意可知△BEC和△BDC均为直角三角形,
∵ 在Rt△BEC和Rt△CDB中,
∴ Rt△BEC≌ Rt△CDB(AAS).
∠ABC =∠ACB ,
BC = BC ,
∠BEC =∠CDB=90° ,
AAS
ABC
CDA
∠A=∠A'
∠B=∠B'
BC=B'C'
AAS
归纳总结
课堂小结
第二章 三角形
2.5 第4课时 全等三角形的判定3——“AAS”
情景引入
如图,在△ABC和 中,如果∠A=∠A′, ∠B= ∠B′, ,那么△ABC和 全等吗?
根据三角形内角和定理,可将上述条件转化为满足“ASA”的条件,从而可以证明△ABC≌
在△ABC和 中,
∵ ∠A = ∠A′,∠B = ∠B′,
∴ ∠C =∠C′.
又∵ ,∠B=∠B′,
∴ (ASA).
由此得到判定两个三角形全等的定理:
两角分别相等且其中一组等角的对边相等的两个三角形全等.
通常可简写成“角角边”或“AAS”.
获取新知
例1 已知:如图,∠B=∠D,∠1=∠2,求证:△ABC≌△ADC.
证明 ∵∠1 =∠2,
∴∠ACB=∠ACD(同角的补角相等).
在△ABC和△ADC中,
∴ △ABC≌△ADC (AAS).
∠B =∠D,
∠ACB =∠ACD,
AC = AC,
例题讲解
例2 已知:如图,点B,F,C,E在同一条直线上,AC∥FD,∠A=∠D,BF=EC.求证:△ABC≌△DEF.
证明 ∵ AC∥FD,
∴∠ACB =∠DFE.
∵ BF= EC,
∴ BF+FC=EC+FC,
即 BC=EF .
在△ABC 和△DEF中,
∴ △ABC≌△DEF(AAS).
∠A =∠D,
∠ACB =∠DFE,
BC = EF,
1. 已知:如图,∠1=∠2,AD=AE. 求证:△ADC≌△AEB.
∴ △ADC≌△AEB(AAS).
∠1 =∠2,
∠A =∠ A,
AD = AE,
证明
∵ 在△ADC 和△AEB中,
随堂演练
2. 已知:在△ABC中,∠ABC =∠ACB,BD⊥AC于点D,CE⊥AB于点E. 求证:BD=CE.
证明 由题意可知△BEC和△BDC均为直角三角形,
∵ 在Rt△BEC和Rt△CDB中,
∴ Rt△BEC≌ Rt△CDB(AAS).
∠ABC =∠ACB ,
BC = BC ,
∠BEC =∠CDB=90° ,
AAS
ABC
CDA
∠A=∠A'
∠B=∠B'
BC=B'C'
AAS
归纳总结
课堂小结
同课章节目录
