2021-2022 北师大版 数学 九年级下册 3.5 确定圆的条件 课件(共26张PPT)
文档属性
| 名称 | 2021-2022 北师大版 数学 九年级下册 3.5 确定圆的条件 课件(共26张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-20 10:50:54 | ||
图片预览



文档简介
(共26张PPT)
5 确定圆的条件
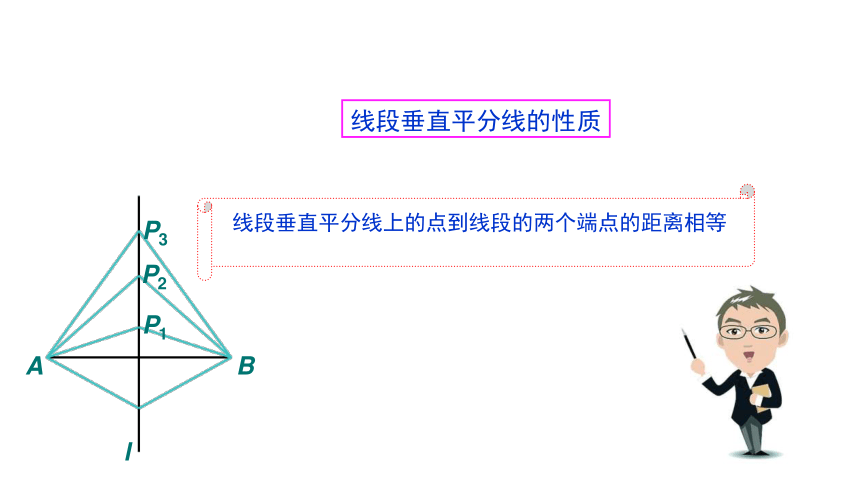
利用尺规,作线段AB的垂直平分线.
作法:
1.分别以点A和点B为圆心,以大于
AB一半的长为半径作弧,
已知:线段AB.
求作:AB的垂直平分线.
2.作直线CD.直线CD就是线段AB的垂直平分线.
两弧相交于点C和D;
A
B
C
D
A
B
l
P1
P2
P3
线段垂直平分线上的点到线段的两个端点的距离相等
线段垂直平分线的性质
1.了解不在同一直线上的三个点确定一个圆,以及 过不在同一直线上的三个点作圆的方法.
2.了解三角形的外接圆、三角形的外心等概念.
3.经历不在同一直线上的三个点确定一个圆的探索过程,培养学生的探索能力.
一位考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
要确定一个圆必须满足几个条件
想一想
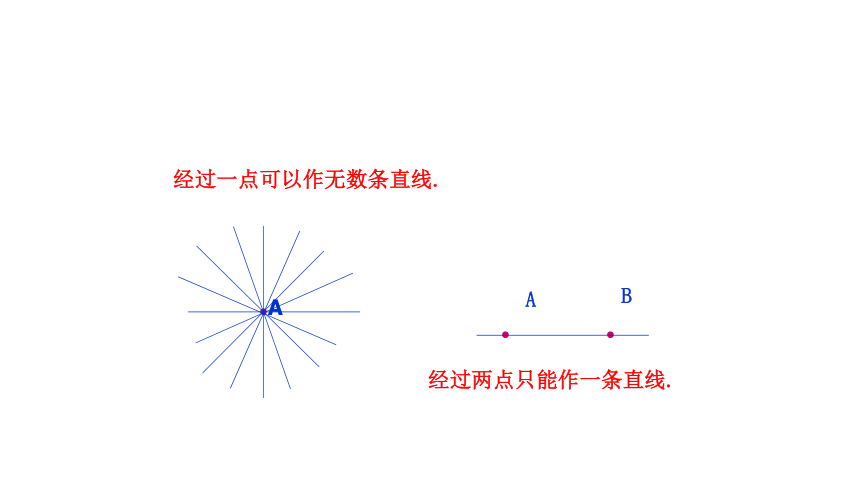
1.过一点可以作几条直线?
2.过几点可确定一条直线?
过几点可以确定一个圆呢?
经过两点只能作一条直线.
●A
●
●
经过一点可以作无数条直线.
A
B
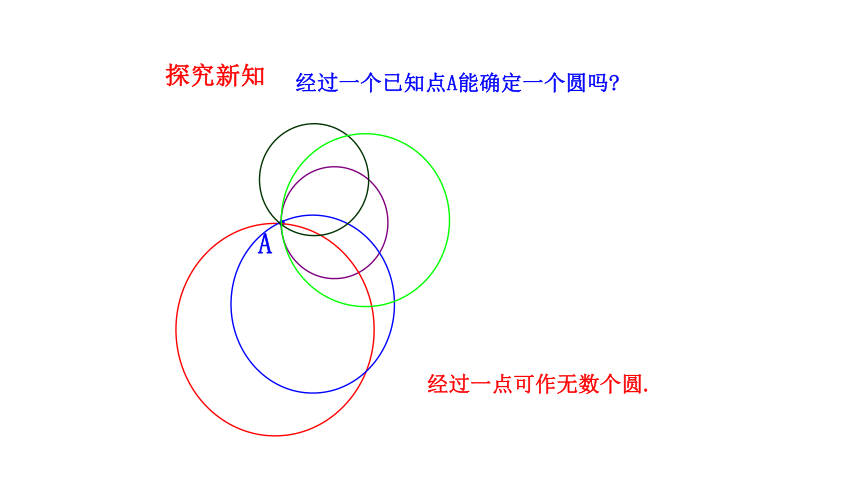
经过一个已知点A能确定一个圆吗
A
经过一点可作无数个圆.
探究新知
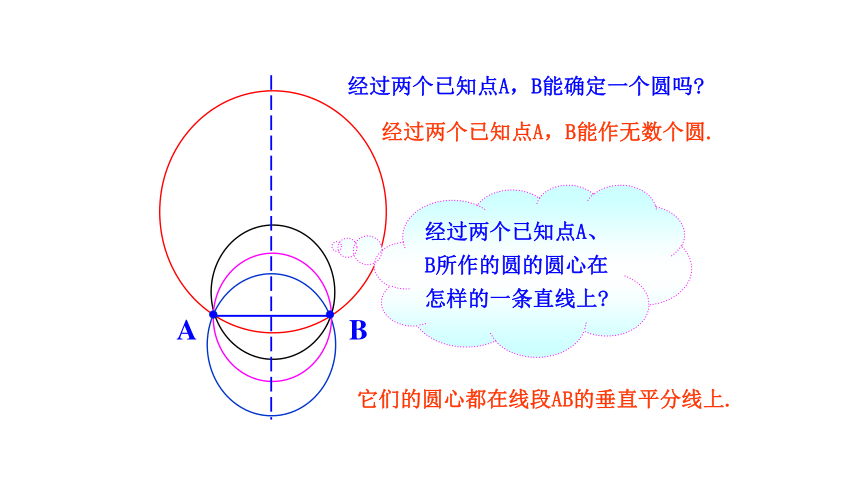
经过两个已知点A,B能确定一个圆吗
A
B
经过两个已知点A、B所作的圆的圆心在怎样的一条直线上
它们的圆心都在线段AB的垂直平分线上.
经过两个已知点A,B能作无数个圆.
1.经过两点A,B的圆的圆心在线段AB的垂直平分线上.
2.以线段AB的垂直平分线上的任意一点为圆心,这点到A或B的距离为半径作圆.
你准备如何(确定圆心,半径)作圆?
其圆心的分布有什么特点 与线段AB有什么关系?
●A
●B
●O
●O
●O
●O
结论:
过已知点A,B作圆,可以作无数个圆.
经过三个已知点A,B,C能确定一个圆吗?
假设经过A,B,C三点的⊙O存在
(1)圆心O到A,B,C三点距离
(填“相等”或“不相等”).
(2)连接AB,AC,过O点 分别作直线MN⊥AB, EF⊥AC,则MN是AB的 .EF是AC的 .
(3)AB,AC的垂直平分线的交点O到B,C的距离 .
N
M
F
E
O
A
B
C
相等
垂直平分线
垂直平分线
相等
A
B
C
议一议
过如下三点能不能作一个圆 为什么
不在同一条直线上的三个点确定一个圆
已知:不在同一直线上的三点A,B,C,
求作: ⊙O使它经过点A,B,C.
作法:1.连接AB,作线段AB的垂直平分线MN.
2.连接AC,作线段AC的垂直平分线EF,交MN于点O.
3.以O为圆心,OB为半径作圆.⊙O就是所求作的圆.
O
N
M
F
E
A
B
C
【例题】
现在你知道怎样将一个如图所示的破损圆盘复原吗?
方法:
1.在圆弧上任取三点A,B,C.
2.作线段AB,BC的垂直平分线,其交点O即为圆心.
3.以点O为圆心,OC的长为半径作圆.
⊙O即为所求.
A
B
C
O
【跟踪训练】
已知△ABC,用直尺和圆规作出过点A,B,C的圆.
A
B
C
O
想一想
定义:经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等.
C
A
B
O
锐角三角形的外心位于三角形内.
直角三角形的外心位于直角三角形斜边中点.
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
【归纳升华】
1.某一个城市在一块空地新建了三个居民小区,它们分别为A,B,C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等.请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?
●
●
●
B
A
C
提示:作△ABC的外心.
【巩固练习】
2.某市要建一个圆形公园,要求公园刚好把动物园A,植物园B和人工湖C包括在内,又要使这个圆形的面积最小,请你给出这个公园的施工图.(A,B,C不在同一直线上)
植物园
动物园
人工湖
提示:作△ABC的外接圆.
C
A
B
1.确定圆的条件——
不在同一直线上的三点
圆心、半径
2. 锐角三角形 在三角形的内部
直角三角形 --外心的位置--- 在斜边上
钝角三角形 在三角形的外部
D
B
【答案】A
B
B
5 确定圆的条件
利用尺规,作线段AB的垂直平分线.
作法:
1.分别以点A和点B为圆心,以大于
AB一半的长为半径作弧,
已知:线段AB.
求作:AB的垂直平分线.
2.作直线CD.直线CD就是线段AB的垂直平分线.
两弧相交于点C和D;
A
B
C
D
A
B
l
P1
P2
P3
线段垂直平分线上的点到线段的两个端点的距离相等
线段垂直平分线的性质
1.了解不在同一直线上的三个点确定一个圆,以及 过不在同一直线上的三个点作圆的方法.
2.了解三角形的外接圆、三角形的外心等概念.
3.经历不在同一直线上的三个点确定一个圆的探索过程,培养学生的探索能力.
一位考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
要确定一个圆必须满足几个条件
想一想
1.过一点可以作几条直线?
2.过几点可确定一条直线?
过几点可以确定一个圆呢?
经过两点只能作一条直线.
●A
●
●
经过一点可以作无数条直线.
A
B
经过一个已知点A能确定一个圆吗
A
经过一点可作无数个圆.
探究新知
经过两个已知点A,B能确定一个圆吗
A
B
经过两个已知点A、B所作的圆的圆心在怎样的一条直线上
它们的圆心都在线段AB的垂直平分线上.
经过两个已知点A,B能作无数个圆.
1.经过两点A,B的圆的圆心在线段AB的垂直平分线上.
2.以线段AB的垂直平分线上的任意一点为圆心,这点到A或B的距离为半径作圆.
你准备如何(确定圆心,半径)作圆?
其圆心的分布有什么特点 与线段AB有什么关系?
●A
●B
●O
●O
●O
●O
结论:
过已知点A,B作圆,可以作无数个圆.
经过三个已知点A,B,C能确定一个圆吗?
假设经过A,B,C三点的⊙O存在
(1)圆心O到A,B,C三点距离
(填“相等”或“不相等”).
(2)连接AB,AC,过O点 分别作直线MN⊥AB, EF⊥AC,则MN是AB的 .EF是AC的 .
(3)AB,AC的垂直平分线的交点O到B,C的距离 .
N
M
F
E
O
A
B
C
相等
垂直平分线
垂直平分线
相等
A
B
C
议一议
过如下三点能不能作一个圆 为什么
不在同一条直线上的三个点确定一个圆
已知:不在同一直线上的三点A,B,C,
求作: ⊙O使它经过点A,B,C.
作法:1.连接AB,作线段AB的垂直平分线MN.
2.连接AC,作线段AC的垂直平分线EF,交MN于点O.
3.以O为圆心,OB为半径作圆.⊙O就是所求作的圆.
O
N
M
F
E
A
B
C
【例题】
现在你知道怎样将一个如图所示的破损圆盘复原吗?
方法:
1.在圆弧上任取三点A,B,C.
2.作线段AB,BC的垂直平分线,其交点O即为圆心.
3.以点O为圆心,OC的长为半径作圆.
⊙O即为所求.
A
B
C
O
【跟踪训练】
已知△ABC,用直尺和圆规作出过点A,B,C的圆.
A
B
C
O
想一想
定义:经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等.
C
A
B
O
锐角三角形的外心位于三角形内.
直角三角形的外心位于直角三角形斜边中点.
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
【归纳升华】
1.某一个城市在一块空地新建了三个居民小区,它们分别为A,B,C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等.请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?
●
●
●
B
A
C
提示:作△ABC的外心.
【巩固练习】
2.某市要建一个圆形公园,要求公园刚好把动物园A,植物园B和人工湖C包括在内,又要使这个圆形的面积最小,请你给出这个公园的施工图.(A,B,C不在同一直线上)
植物园
动物园
人工湖
提示:作△ABC的外接圆.
C
A
B
1.确定圆的条件——
不在同一直线上的三点
圆心、半径
2. 锐角三角形 在三角形的内部
直角三角形 --外心的位置--- 在斜边上
钝角三角形 在三角形的外部
D
B
【答案】A
B
B
