北师大版九年级下册 1.1.2 锐角三角函数课件(共37张PPT)
文档属性
| 名称 | 北师大版九年级下册 1.1.2 锐角三角函数课件(共37张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-20 00:00:00 | ||
图片预览




文档简介
(共37张PPT)
1 锐角三角函数
第2课时
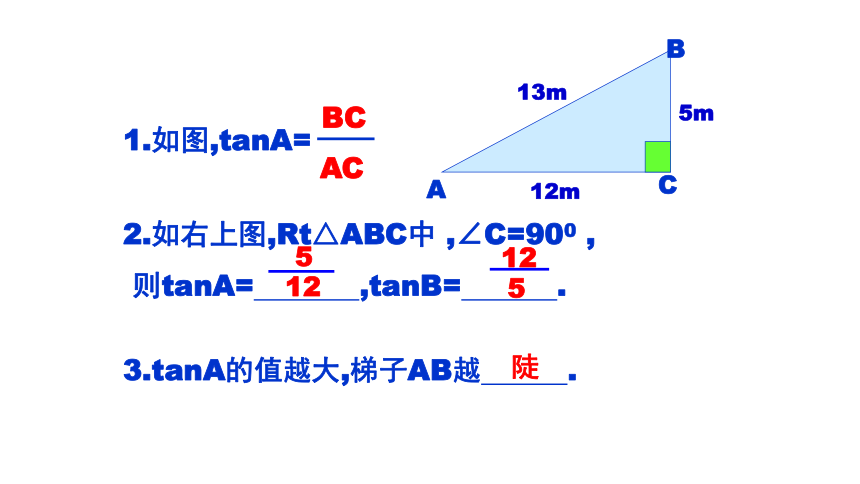
在直角三角形中锐角的大小和它的对边与邻边的比值有密切关系:在Rt△ABC中,锐角A的对边与邻边的比
叫做∠A的正切,记作tan A,
即
tan A=
A
B
C
∠A的对边
∠A的邻边
┌
斜边
2.如右上图,Rt△ABC中 ,∠C=900 ,
则tanA= ,tanB= .
5
12
12
5
5m
13m
A
B
C
12m
1.如图,tanA=
BC
AC
3.tanA的值越大,梯子AB越 .
陡
1.经历探索直角三角形中边角关系的过程,理解正弦和余弦的意义.
2.能够运用sin A,cos A表示直角三角形两边的比.
3.能根据直角三角形中的边角关系进行简单的计算.
4.理解锐角三角函数的意义.
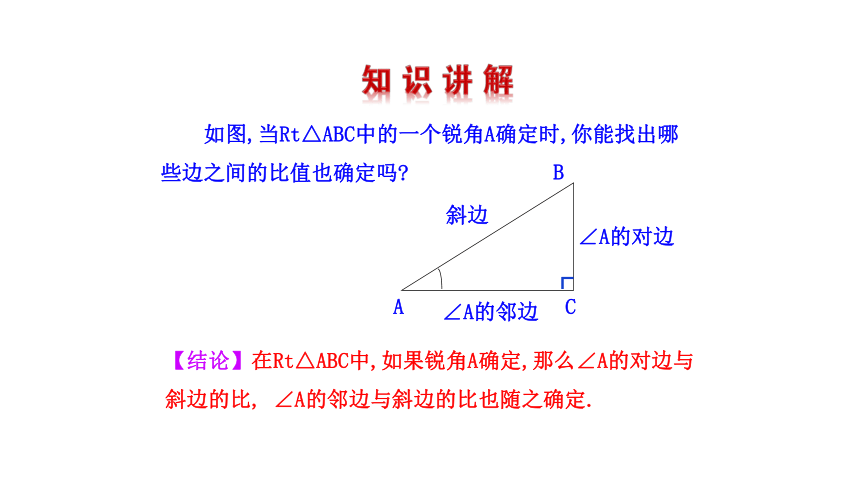
如图,当Rt△ABC中的一个锐角A确定时,你能找出哪些边之间的比值也确定吗
【结论】在Rt△ABC中,如果锐角A确定,那么∠A的对边与斜边的比, ∠A的邻边与斜边的比也随之确定.
B
┌
斜边
A
C
∠A的对边
∠A的邻边
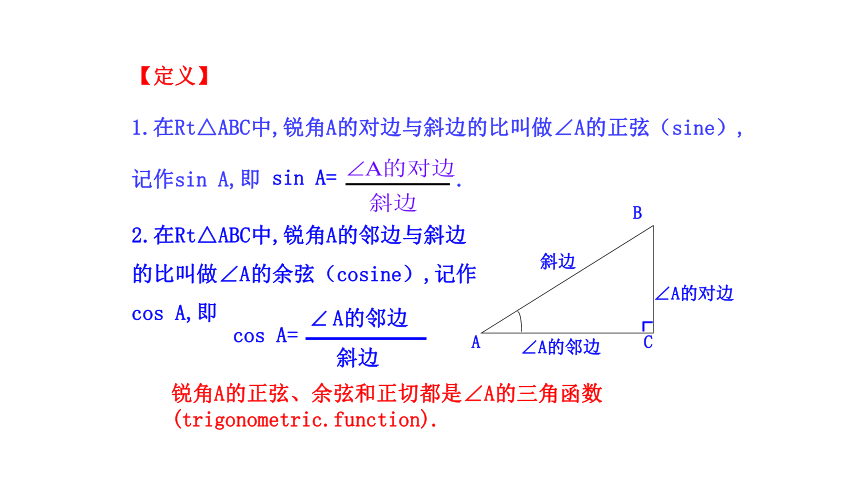
【定义】
1.在Rt△ABC中,锐角A的对边与斜边的比叫做∠A的正弦(sine),
记作sin A,即 .
2.在Rt△ABC中,锐角A的邻边与斜边
的比叫做∠A的余弦(cosine),记作cos A,即
锐角A的正弦、余弦和正切都是∠A的三角函数(trigonometric.function).
A
B
C
∠A的对边
∠A的邻边
┌
斜边
cos A=
斜边
A的邻边
sin A=
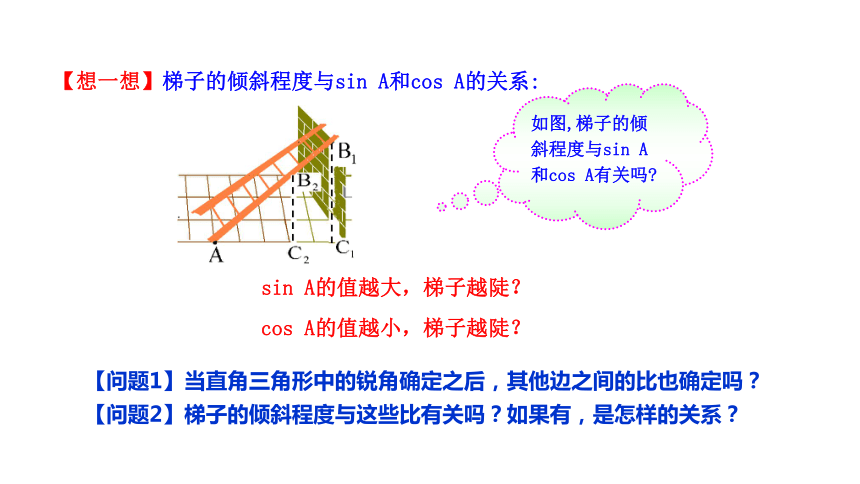
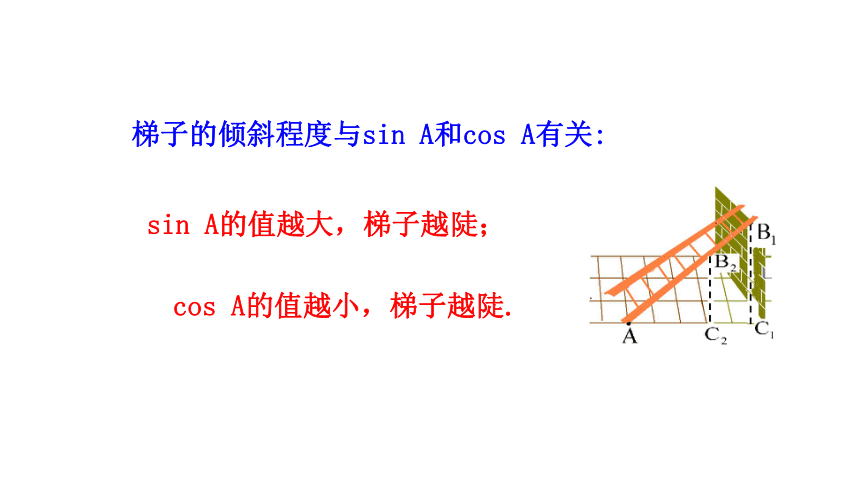
【想一想】梯子的倾斜程度与sin A和cos A的关系:
cos A的值越小,梯子越陡?
sin A的值越大,梯子越陡?
如图,梯子的倾斜程度与sin A和cos A有关吗
【问题1】当直角三角形中的锐角确定之后,其他边之间的比也确定吗?
【问题2】梯子的倾斜程度与这些比有关吗?如果有,是怎样的关系?
(2) 和 有什么关系? 和 呢?
想一想:如图.
(1)直角三角形A1B1C1和直角三角形A1B2C2有什么关系?
(3)如果改变B2在梯子A1B1上的位置呢?由此你可得出什么结论?
(4)如果改变梯子A1B1的倾斜角的大小呢?由此你可得出什么结论?
C1
C2
A1
B1
B2
C1
C2
A1
B1
B2
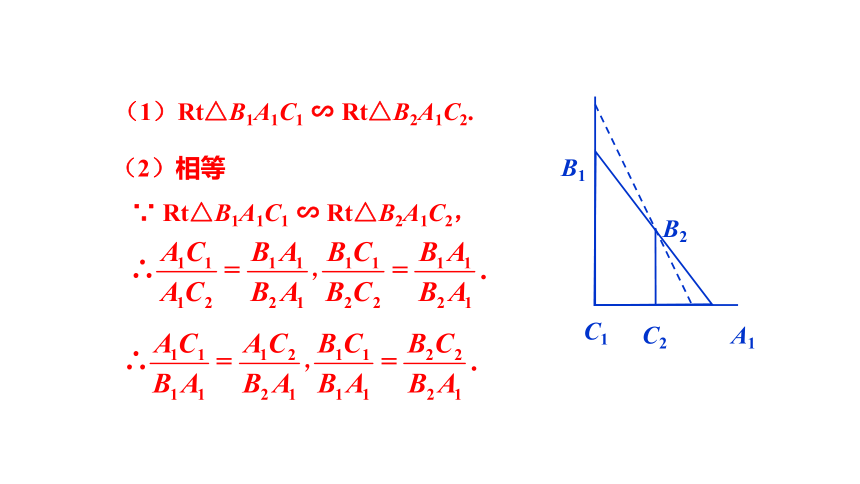
(1)Rt△B1A1C1 ∽ Rt△B2A1C2.
(2)相等
∵ Rt△B1A1C1 ∽ Rt△B2A1C2,
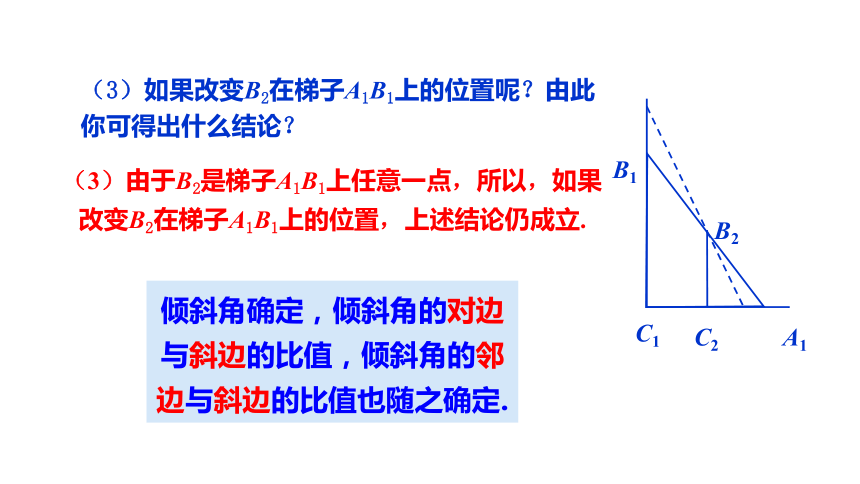
(3)由于B2是梯子A1B1上任意一点,所以,如果改变B2在梯子A1B1上的位置,上述结论仍成立.
C1
C2
A1
B1
B2
倾斜角确定,倾斜角的对边与斜边的比值,倾斜角的邻边与斜边的比值也随之确定.
(3)如果改变B2在梯子A1B1上的位置呢?由此你可得出什么结论?
(4)改变梯子A1B1的倾斜角,也就是改变虚线的位置,可知:
C1
C2
A1
B1
B2
当倾斜角变大时,对边与斜边的比会变大;
邻边与斜边的比会变小;
当倾斜角变小时,对边与斜边的比会变小;
邻边与斜边的比会变大
(4)如果改变梯子A1B1的倾斜角的大小呢?由此你可得出什么结论?
梯子的倾斜程度与sin A和cos A有关:
cos A的值越小,梯子越陡.
sin A的值越大,梯子越陡;
例1.如图,在Rt△ABC中,∠B=90°,AC=200,sin A=0.6.
求BC的长.
请你求出cos A,tan A,sin C,cos C和tan C的值.你敢应战吗
A
C
B
┌
解:在Rt△ABC中
【例题】
【解析】
cos A=
tan A=
cos C=
sin C=
tan C=
知识点1 根据定义求锐角的正弦值
1.在Rt△ABC中,∠C=90°,AB=4,BC=3,则sin B的值为( )
A
2.在下列网格中,若小正方形的边长均为1,点A,B,O都在格点上,则∠A的正弦值是( )
C
3.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB交AB于点D.下列各组的比不等于sin ∠BCD的是( )
C
知识点2 根据定义求锐角的余弦值
4.如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,则cos B的值为( )
B
B
知识点3 锐角三角函数
6.如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,AC=5,则下列三角函数表示正确的是( )
A
例2.如图:在Rt△ABC中,∠C=90°,AC=10,
求AB,sinB.
你发现了什么?
在直角三角形中,一个锐角的正弦等于另一个锐角的余弦.
A
B
C
1.如图:在等腰三角形ABC中,AB=AC=5,BC=6.求: sin B,cos B,tan B.
温馨提示:过点A作AD垂直BC于点D.构造直角三角形.
5
5
6
A
B
C
D
【跟踪训练】
【解析】过点A作AD垂直BC于点D,则BD=CD=3,根据勾股定理得AD=4,
sin B=
cos B=
tan B=
C
D
D
5.(宜昌·中考)△ABC在网格中的位置如图所示(每个小正方形的边长均为1),AD⊥BC于点D.下列四个选项中,错误的是( )
A.sin α=cosα B.tanC=2 C.sin β=cosβ D.tanα=1
C
60
7.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,sin A的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
8.已知∠A,∠B为锐角
(1)若∠A=∠B,则sin A sin B.
(2)若sin A=sin B,则∠A ∠B.
A
B
C
┌
C
=
=
9.如图, ∠ACB=90°,CD⊥AB.若BD=6,CD=12.求cos A的值.
A
C
B
D
【解析】cos A=sinB=
1.锐角三角函数的定义:在Rt△ABC中,∠C=90°.
即在直角三角形中,一个锐角的正弦等于另一个锐角的余弦.
2.在Rt△ABC中,sin A=cos B.
【规律方法】 在定义中应该注意的几个问题:
(1) sin A,cos A,tan A 是在直角三角形中定义的,∠A 是锐角
(注意数形结合,构造直角三角形) .
(2)sin A,cos A,tan A 是三个完整的符号,表示∠A的正弦,余弦,正切,习惯省去“∠”这个符号.
(3)sin A,cos A,tan A 都是比值.注意比的顺序,且sin A,cos A,tan A 均大于0,无单位.
(4)sin A,cos A,tan A 的值只与∠A的大小有关,而与直角三角形的边长大小无关.
(5)角相等,则其三角函数值相等;两锐角的同一三角函数值相等,则这两个锐角相等.
1.(温州·中考)如图,在△ABC中,∠C=90°,
AB=13,BC=5,则sin A的值是( )
A. B. C. D.
【解析】由正弦的定义可得.
A
C
B
A
2.(常德·中考)在Rt△ABC中,∠C=90°,若AC=2BC,则
sin A的值是( )
B.2
D.
C
A.
C.
3.(三明·中考)如图,在梯形ABCD中,AD//BC,AC⊥AB,AD=CD , ,BC=10,则AB的值是( )
A.9 B.8 C.6 D.3
C
4.(毕节·中考)在正方形网格中,△ABC的位置如图所示,则 的值为( )
A.
B.
C.
D.
B
5.(建设兵团·中考) 如图(1)是一张Rt△ABC纸片,如果用两张相同的这种纸片恰好能拼成一个等边三角形,如图(2),那么在Rt△ABC中,sin B的值是( )
B.
C. 1 D.
B
A.
D
B
8.【2020·杭州】如图,在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( )
A.c=bsin B B.b=csin B
C.a=btan B D.b=ctan B
B
1 锐角三角函数
第2课时
在直角三角形中锐角的大小和它的对边与邻边的比值有密切关系:在Rt△ABC中,锐角A的对边与邻边的比
叫做∠A的正切,记作tan A,
即
tan A=
A
B
C
∠A的对边
∠A的邻边
┌
斜边
2.如右上图,Rt△ABC中 ,∠C=900 ,
则tanA= ,tanB= .
5
12
12
5
5m
13m
A
B
C
12m
1.如图,tanA=
BC
AC
3.tanA的值越大,梯子AB越 .
陡
1.经历探索直角三角形中边角关系的过程,理解正弦和余弦的意义.
2.能够运用sin A,cos A表示直角三角形两边的比.
3.能根据直角三角形中的边角关系进行简单的计算.
4.理解锐角三角函数的意义.
如图,当Rt△ABC中的一个锐角A确定时,你能找出哪些边之间的比值也确定吗
【结论】在Rt△ABC中,如果锐角A确定,那么∠A的对边与斜边的比, ∠A的邻边与斜边的比也随之确定.
B
┌
斜边
A
C
∠A的对边
∠A的邻边
【定义】
1.在Rt△ABC中,锐角A的对边与斜边的比叫做∠A的正弦(sine),
记作sin A,即 .
2.在Rt△ABC中,锐角A的邻边与斜边
的比叫做∠A的余弦(cosine),记作cos A,即
锐角A的正弦、余弦和正切都是∠A的三角函数(trigonometric.function).
A
B
C
∠A的对边
∠A的邻边
┌
斜边
cos A=
斜边
A的邻边
sin A=
【想一想】梯子的倾斜程度与sin A和cos A的关系:
cos A的值越小,梯子越陡?
sin A的值越大,梯子越陡?
如图,梯子的倾斜程度与sin A和cos A有关吗
【问题1】当直角三角形中的锐角确定之后,其他边之间的比也确定吗?
【问题2】梯子的倾斜程度与这些比有关吗?如果有,是怎样的关系?
(2) 和 有什么关系? 和 呢?
想一想:如图.
(1)直角三角形A1B1C1和直角三角形A1B2C2有什么关系?
(3)如果改变B2在梯子A1B1上的位置呢?由此你可得出什么结论?
(4)如果改变梯子A1B1的倾斜角的大小呢?由此你可得出什么结论?
C1
C2
A1
B1
B2
C1
C2
A1
B1
B2
(1)Rt△B1A1C1 ∽ Rt△B2A1C2.
(2)相等
∵ Rt△B1A1C1 ∽ Rt△B2A1C2,
(3)由于B2是梯子A1B1上任意一点,所以,如果改变B2在梯子A1B1上的位置,上述结论仍成立.
C1
C2
A1
B1
B2
倾斜角确定,倾斜角的对边与斜边的比值,倾斜角的邻边与斜边的比值也随之确定.
(3)如果改变B2在梯子A1B1上的位置呢?由此你可得出什么结论?
(4)改变梯子A1B1的倾斜角,也就是改变虚线的位置,可知:
C1
C2
A1
B1
B2
当倾斜角变大时,对边与斜边的比会变大;
邻边与斜边的比会变小;
当倾斜角变小时,对边与斜边的比会变小;
邻边与斜边的比会变大
(4)如果改变梯子A1B1的倾斜角的大小呢?由此你可得出什么结论?
梯子的倾斜程度与sin A和cos A有关:
cos A的值越小,梯子越陡.
sin A的值越大,梯子越陡;
例1.如图,在Rt△ABC中,∠B=90°,AC=200,sin A=0.6.
求BC的长.
请你求出cos A,tan A,sin C,cos C和tan C的值.你敢应战吗
A
C
B
┌
解:在Rt△ABC中
【例题】
【解析】
cos A=
tan A=
cos C=
sin C=
tan C=
知识点1 根据定义求锐角的正弦值
1.在Rt△ABC中,∠C=90°,AB=4,BC=3,则sin B的值为( )
A
2.在下列网格中,若小正方形的边长均为1,点A,B,O都在格点上,则∠A的正弦值是( )
C
3.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB交AB于点D.下列各组的比不等于sin ∠BCD的是( )
C
知识点2 根据定义求锐角的余弦值
4.如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,则cos B的值为( )
B
B
知识点3 锐角三角函数
6.如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,AC=5,则下列三角函数表示正确的是( )
A
例2.如图:在Rt△ABC中,∠C=90°,AC=10,
求AB,sinB.
你发现了什么?
在直角三角形中,一个锐角的正弦等于另一个锐角的余弦.
A
B
C
1.如图:在等腰三角形ABC中,AB=AC=5,BC=6.求: sin B,cos B,tan B.
温馨提示:过点A作AD垂直BC于点D.构造直角三角形.
5
5
6
A
B
C
D
【跟踪训练】
【解析】过点A作AD垂直BC于点D,则BD=CD=3,根据勾股定理得AD=4,
sin B=
cos B=
tan B=
C
D
D
5.(宜昌·中考)△ABC在网格中的位置如图所示(每个小正方形的边长均为1),AD⊥BC于点D.下列四个选项中,错误的是( )
A.sin α=cosα B.tanC=2 C.sin β=cosβ D.tanα=1
C
60
7.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,sin A的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
8.已知∠A,∠B为锐角
(1)若∠A=∠B,则sin A sin B.
(2)若sin A=sin B,则∠A ∠B.
A
B
C
┌
C
=
=
9.如图, ∠ACB=90°,CD⊥AB.若BD=6,CD=12.求cos A的值.
A
C
B
D
【解析】cos A=sinB=
1.锐角三角函数的定义:在Rt△ABC中,∠C=90°.
即在直角三角形中,一个锐角的正弦等于另一个锐角的余弦.
2.在Rt△ABC中,sin A=cos B.
【规律方法】 在定义中应该注意的几个问题:
(1) sin A,cos A,tan A 是在直角三角形中定义的,∠A 是锐角
(注意数形结合,构造直角三角形) .
(2)sin A,cos A,tan A 是三个完整的符号,表示∠A的正弦,余弦,正切,习惯省去“∠”这个符号.
(3)sin A,cos A,tan A 都是比值.注意比的顺序,且sin A,cos A,tan A 均大于0,无单位.
(4)sin A,cos A,tan A 的值只与∠A的大小有关,而与直角三角形的边长大小无关.
(5)角相等,则其三角函数值相等;两锐角的同一三角函数值相等,则这两个锐角相等.
1.(温州·中考)如图,在△ABC中,∠C=90°,
AB=13,BC=5,则sin A的值是( )
A. B. C. D.
【解析】由正弦的定义可得.
A
C
B
A
2.(常德·中考)在Rt△ABC中,∠C=90°,若AC=2BC,则
sin A的值是( )
B.2
D.
C
A.
C.
3.(三明·中考)如图,在梯形ABCD中,AD//BC,AC⊥AB,AD=CD , ,BC=10,则AB的值是( )
A.9 B.8 C.6 D.3
C
4.(毕节·中考)在正方形网格中,△ABC的位置如图所示,则 的值为( )
A.
B.
C.
D.
B
5.(建设兵团·中考) 如图(1)是一张Rt△ABC纸片,如果用两张相同的这种纸片恰好能拼成一个等边三角形,如图(2),那么在Rt△ABC中,sin B的值是( )
B.
C. 1 D.
B
A.
D
B
8.【2020·杭州】如图,在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( )
A.c=bsin B B.b=csin B
C.a=btan B D.b=ctan B
B
