2021-2022 北师大版 数学 九年级下册 1.6 利用三角函数测高 课件(共40张PPT)
文档属性
| 名称 | 2021-2022 北师大版 数学 九年级下册 1.6 利用三角函数测高 课件(共40张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-20 22:42:08 | ||
图片预览





文档简介
(共40张PPT)
6 利用三角函数测高
30°
0°
60°
90°
90°
60°
30°
直角三角形两锐角的关系:两锐角互余 ∠A+∠B=90°.
直角三角形三边的关系: 勾股定理 a2+b2=c2.
b
A
B
C
a
┌
c
直角三角形边与角之间的关系:锐角三角函数
直角三角形的边角关系
特殊角:30°,45°,60°角的三角函数值.
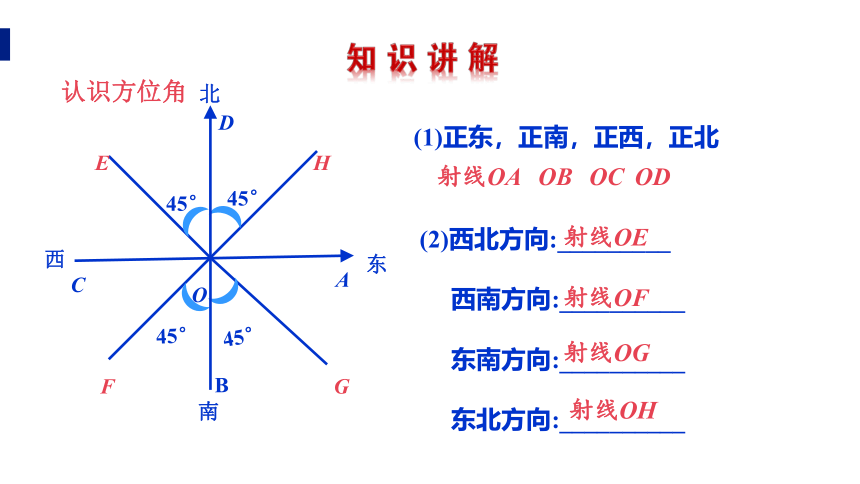
1.仰角、俯角:
铅垂线
仰角
俯角
水平线
视线
视线
b
A
B
C
a
┌
c
2.直角三角形的边角关系:
1.经历探索船是否有触礁危险的过程,进一步体会三角函数在解决问题过程中的应用.
2.能够设计测量方案,说明测量理由,能够综合运用直角三角形边角关系的知识解决实际问题.
3.能够把实际问题转化为数学问题,能够借助于计算器进行有关三角函数的计算,并能对结果的意义进行说明.
东
西
北
南
O
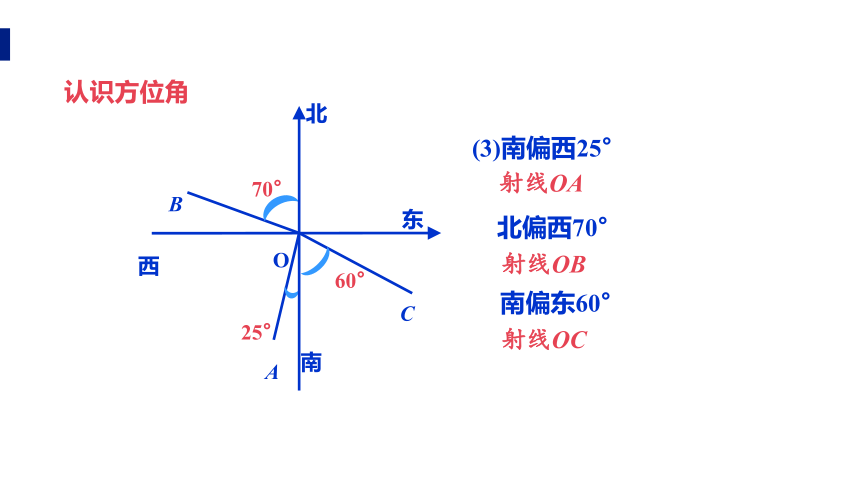
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OA
A
B
C
D
OB
OC
OD
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
认识方位角
O
北
南
西
东
(3)南偏西25°
25°
北偏西70°
南偏东60°
A
B
C
射线OA
射线OB
射线OC
70°
60°
认识方位角
你认为货船继续向西航行途中会有触礁的危险吗
B
25
C
20
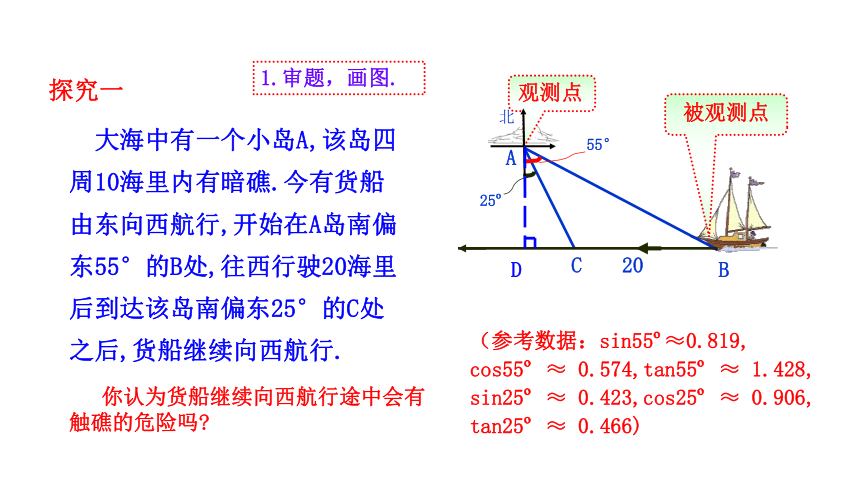
1.审题,画图.
大海中有一个小岛A,该岛四周10海里内有暗礁.今有货船由东向西航行,开始在A岛南偏东55°的B处,往西行驶20海里后到达该岛南偏东25°的C处之后,货船继续向西航行.
55°
被观测点
A
(参考数据:sin55 ≈0.819,
cos55 ≈ 0.574,tan55 ≈ 1.428,
sin25 ≈ 0.423,cos25 ≈ 0.906,
tan25 ≈ 0.466)
北
D
观测点
探究一
B
C
20
D
A
x
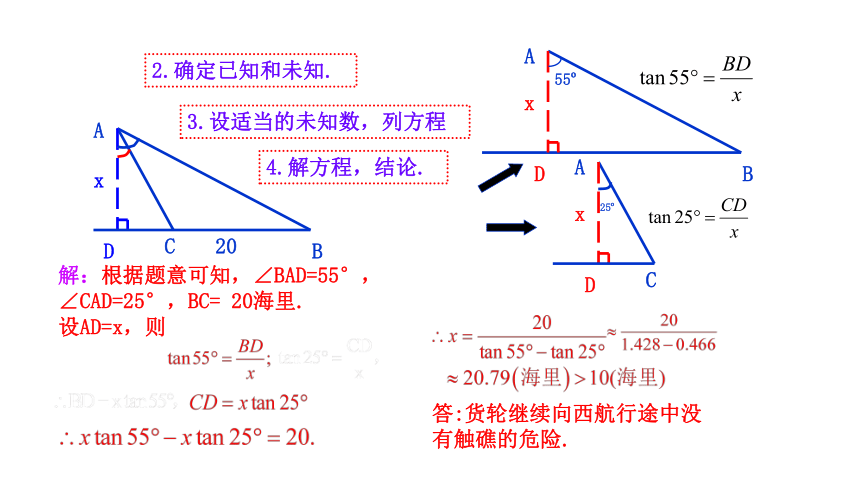
2.确定已知和未知.
3.设适当的未知数,列方程
C
D
A
x
25
解:根据题意可知,∠BAD=55°,
∠CAD=25°,BC= 20海里.
设AD=x,则
答:货轮继续向西航行途中没有触礁的危险.
4.解方程,结论.
55
B
D
A
x
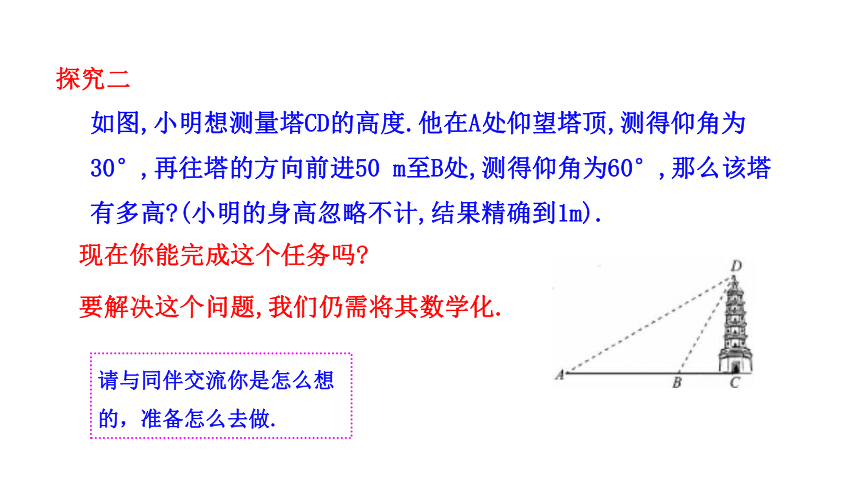
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50 m至B处,测得仰角为60°,那么该塔有多高 (小明的身高忽略不计,结果精确到1m).
请与同伴交流你是怎么想的,准备怎么去做.
现在你能完成这个任务吗
要解决这个问题,我们仍需将其数学化.
探究二
D
A
B
C
┌
50 m
30°
60°
答:该塔约有43 m高.
解:如图,根据题意可知,∠A=30°,∠DBC=60°,
AB=50 m.设CD=x m,则∠ADC=60°,∠BDC=30°,
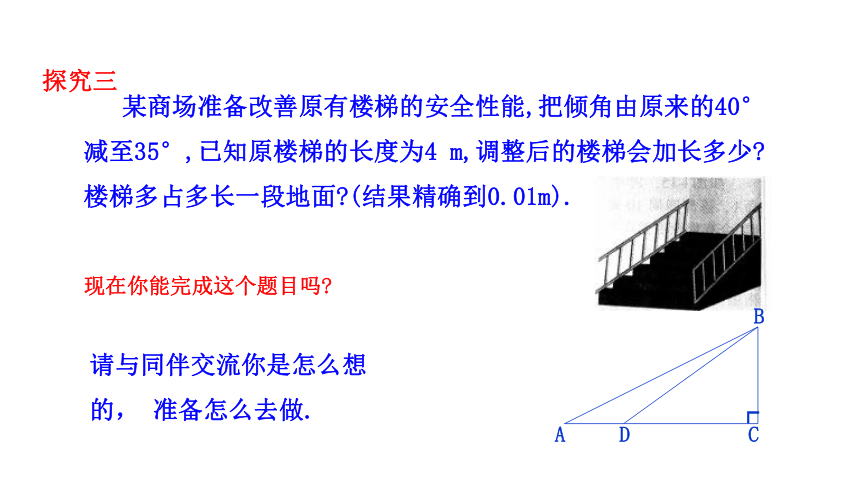
某商场准备改善原有楼梯的安全性能,把倾角由原来的40°减至35°,已知原楼梯的长度为4 m,调整后的楼梯会加长多少 楼梯多占多长一段地面 (结果精确到0.01m).
现在你能完成这个题目吗
请与同伴交流你是怎么想的, 准备怎么去做.
A
B
C
D
┌
探究三
解:(1)如图,根据题意可知,∠A=35°,
∠BDC=40°,DB=4m.
A
B
C
D
┌
4m
35°
40°
答:调整后的楼梯会加长约0.48m.
(2)如图,根据题意可知,∠A=35°,∠BDC=40°,DB=4m.
答:楼梯多占约0.61m长的一段地面.
A
B
C
D
┌
4m
35°
40°
如图,一灯柱AB被一钢缆CD固定.CD与地面成40°夹角,且DB=5m.现再在C点上方2m处加固另一条钢缆ED,那么,钢缆ED的长度为多少 (结果精确到0.01m).
探究四
解:如图,根据题意可知,∠CDB=40°,EC=2m,DB=5m.
∴∠BDE≈51.12°.
E
B
C
D
2 m
40°
5 m
答:钢缆ED的长度约为7.97m.
如图,水库大坝的截面是梯形ABCD,其中AD∥BC,坝顶AD=6 m,坡长CD=8 m.坡底BC=30m,∠ADC=135°.
(1)求∠ABC的大小(精确到1°);
(2)如果坝长100 m,那么修建这个大坝共需多少土石料(结果精确到0.01m3 ).
A
B
C
D
探究五
A
B
C
D
6m
8m
30m
135°
解:(1)过点D作DE⊥BC于点E,过点A作AF⊥BC于点F.
E
┐
F
┌
∴∠ABC≈17°.
答:∠ABC约为17°.
活动一 测量倾斜角(仰角或俯角)
测量倾斜角可以用测倾器,简单的测倾器由度盘、铅锤和支杆组成(如图).
30°
0°
60°
90°
90°
60°
30°
30°
0°
60°
90°
90°
60°
30°
30°
0°
60°
90°
90°
60°
30°
M
水平线
1.把支杆竖直插入地面,使支杆的中心线.铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
2.转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数.
使用测倾器测量倾斜角的步骤如下:
P
Q
活动二 测量底部可以到达的物体的高度.
所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离.
如图,要测量物体MN的高度,
1.在测点A处安置测倾器,
测得M的仰角∠MCE=α.
2.量出测点A到物体底部N的水平距离AN=l.
3.量出测倾器的高度AC=a(即顶线PQ成水平位置时,它与地面的距离).
C
A
E
N
M
可按下列步骤进行:
测量底部可以直接到达的物体的高度
在观测点A安置测倾器,测得M的仰角∠MCE=α
量出观测点A到物体底部N的水平距离AN=L
量出测倾器的高度AC=a,可求出MN的高度.MN=ME+EN=L·tanα+α
A
N
C
M
E
α
L
a
根据刚才测量的数据,你能求出物体MN的高度吗 说说你的理由.
和同伴交流一下你的发现.
在Rt△MCE中,
ME=EC·tanα=AN·tanα=l·tanα
MN=ME+EN=ME+AC=l·tanα+ a
a
C
A
E
N
M
l
α
议一议
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体的底部之间的距离.
要测量物体MN的高度,使用测倾器测一次仰角够吗?
a
α
E
C
A
N
M
活动三 测量底部不可以到达的物体的高度.
要测量物体MN的高度,测一次仰角是不够的.
a
b
α
E
C
A
D
B
β
N
M
还需哪些条件?测量哪些数据?
议一议
如图,要测量物体MN的高度,可以按下列步骤进行:
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α.
2.在测点A与物体之间的B处安置测倾器(A,B与N在一条直线上,且A,B之间的距离可以直接测得), 测得此时M的仰角∠MDE=β.
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.
根据测量数据,你能
求出物体MN的高度吗 说说你的理由.
测量底部不可以直接到达的物体的高度
在测点A处安置测倾器,测得此时M的仰角∠MCE=α
在测点A与物体之间B处安置测倾器,测得此时M的仰角∠MDE=β
量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.根据测量数据,可求出物体MN的高度。
A
C
B
D
M
N
E
α
β
过程:根据测量数据,物体MN的高度计算过程为:
a
b
α
E
C
A
D
B
β
N
M
在Rt△ MDE中,
ED=
在Rt△MCE中,
EC =
EC-ED= - =b
(2)
再求体积!
先算面积!
答:修建这个大坝共需土石料约1 0182.34 m3.
1.(株洲·中考)如图,孔明同学背着一桶水,从山脚A出发,沿与地面成30°角的山坡向上走,送水到山上因今年春季受旱缺水的王奶奶家(B处),AB=80米,则孔明从A到B上升的高度BC是 米.
【解析】依题意得,∠ACB=90°.所以sin A=sin 30°= ,所以BC=40(米).
30°
40
2.(衡阳·中考)为申办冬奥会,需改变哈尔滨市的交通状况.在大直街拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区,现在某工人站在离B点3米远的D处,从C点测得树的顶端A点的仰角为60°,树的底部B点的俯角为30°.
问:距离B点8米远的保护物是否在危险区内?
【解析】在Rt△BDC中,BC=
=2
所以离B点8米远的保护物不在危险区内.
在Rt△ABC中,AB=2BC=4
<8,
3.(湘潭·中考)如图,我护航军舰在某海域航行到B处时,灯塔A在我军舰的北偏东60o的方向;我军舰从B处向正东方向行驶1 800米到达C处,此时灯塔A在我军舰的正北方向.求C处与灯塔A的距离(结果精确到(1米)).
东
北
60o
A
C
B
【解析】在Rt△ABC中,∠C=90°,BC=1 800,∠ABC=30°,
答:C处与灯塔A的距离约为1 039米.
从而
=600
≈1 039(米).
4.(贵阳·中考)某商场为缓解我市“停车难”问题,拟建造地下停车库,如图是该地下停车库坡道入口的设计示意图,其中, AB⊥BD,∠BAD=18°,点C在BD上,BC=0.5 m.根据规定,地下停车库坡道入口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.小明认为CD的长就是所限制的高度,而小亮认为应该以CE的长作为限制的高度.小明和小亮谁说的对?请你判断并计算出正确的结果.(结果精确到0.1m)
【解析】小亮说的对,在△ABD中,∠ABD=90°,
∠BAD=18 °, BA=10 m,
∴tan∠BAD=
∴BD=10×tan 18°,
在Rt△CDE中,∠CDE=90 °
―∠BAD=72°,
∵CE⊥ED∴sin∠CDE=
∴CD=BD―BC=10×tan 18°
―0.5,
―0.5)≈2.6(m)
∴CE=CD×sin∠CDE
=sin72
°×(10×tan 18°
即限制高度为2.6 m.
【规律方法】根据题意画出几何图形,构造直角三角形,灵活运用三角函数的定义结合勾股定理的有关知识是进行解题的关键.
实际问题
图形分析
生活问题数学化
(构造直角三角形)
设未知量
解答问题
(构建三角函数模型)
(代入数据求解)
求解方程
数学问题
建立方程
B
C
600
20
450
D
┐
C
B
A
D
20
┌
300
450
┌
600
450
A
B
C
20
D
┌
300
600
A
B
C
D
20
450
300
B
C
20
A
┌
D
A
测量底部可以到达的
物体的高度,如下图
测量底部不可以直接到达的物体的高度,如下图
1.(宿迁·中考)如图,在Rt△ABC中,∠C=90°, AM是BC边上的中线, 则tan B的值为_____.
2.(孝感·中考)如图,一艘船向正北航行,在A处看到灯塔S在船的北偏东30°的方向上,航行12海里到达B点,在B处看到灯塔S在船的北偏东60°的方向上,此船继续沿正北方向航行过程中距灯塔S的最近距离是_____海里(不作近似计算).
3.(呼和浩特·中考)如图,在△ABC中,∠C=90°,∠B=30°,AD是∠BAC的角平分线,与BC相交于点D,且AB=4 ,求AD的长.
∵ AD平分∠BAC,
【解析】在Rt△ABC中,
AB=
×4
∴ AC=
=
=4.
∴ AD=
∴ 在Rt△ACD中,∠CAD=30°.
∵ ∠B=30°,
4.小明家所在居民楼的对面有一座大厦AB,AB=80米.为测量居民楼与这座大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.(结果保留整数)
(参考数据: )
∵AD+BD = AB,∴
【解析】设CD =x 米.在Rt△ACD中,
在Rt△BCD,tan48°=
解得:x≈43.
答:小明家所在居民楼与大厦的距离CD大约是43米.
则
则
6 利用三角函数测高
30°
0°
60°
90°
90°
60°
30°
直角三角形两锐角的关系:两锐角互余 ∠A+∠B=90°.
直角三角形三边的关系: 勾股定理 a2+b2=c2.
b
A
B
C
a
┌
c
直角三角形边与角之间的关系:锐角三角函数
直角三角形的边角关系
特殊角:30°,45°,60°角的三角函数值.
1.仰角、俯角:
铅垂线
仰角
俯角
水平线
视线
视线
b
A
B
C
a
┌
c
2.直角三角形的边角关系:
1.经历探索船是否有触礁危险的过程,进一步体会三角函数在解决问题过程中的应用.
2.能够设计测量方案,说明测量理由,能够综合运用直角三角形边角关系的知识解决实际问题.
3.能够把实际问题转化为数学问题,能够借助于计算器进行有关三角函数的计算,并能对结果的意义进行说明.
东
西
北
南
O
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OA
A
B
C
D
OB
OC
OD
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
认识方位角
O
北
南
西
东
(3)南偏西25°
25°
北偏西70°
南偏东60°
A
B
C
射线OA
射线OB
射线OC
70°
60°
认识方位角
你认为货船继续向西航行途中会有触礁的危险吗
B
25
C
20
1.审题,画图.
大海中有一个小岛A,该岛四周10海里内有暗礁.今有货船由东向西航行,开始在A岛南偏东55°的B处,往西行驶20海里后到达该岛南偏东25°的C处之后,货船继续向西航行.
55°
被观测点
A
(参考数据:sin55 ≈0.819,
cos55 ≈ 0.574,tan55 ≈ 1.428,
sin25 ≈ 0.423,cos25 ≈ 0.906,
tan25 ≈ 0.466)
北
D
观测点
探究一
B
C
20
D
A
x
2.确定已知和未知.
3.设适当的未知数,列方程
C
D
A
x
25
解:根据题意可知,∠BAD=55°,
∠CAD=25°,BC= 20海里.
设AD=x,则
答:货轮继续向西航行途中没有触礁的危险.
4.解方程,结论.
55
B
D
A
x
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50 m至B处,测得仰角为60°,那么该塔有多高 (小明的身高忽略不计,结果精确到1m).
请与同伴交流你是怎么想的,准备怎么去做.
现在你能完成这个任务吗
要解决这个问题,我们仍需将其数学化.
探究二
D
A
B
C
┌
50 m
30°
60°
答:该塔约有43 m高.
解:如图,根据题意可知,∠A=30°,∠DBC=60°,
AB=50 m.设CD=x m,则∠ADC=60°,∠BDC=30°,
某商场准备改善原有楼梯的安全性能,把倾角由原来的40°减至35°,已知原楼梯的长度为4 m,调整后的楼梯会加长多少 楼梯多占多长一段地面 (结果精确到0.01m).
现在你能完成这个题目吗
请与同伴交流你是怎么想的, 准备怎么去做.
A
B
C
D
┌
探究三
解:(1)如图,根据题意可知,∠A=35°,
∠BDC=40°,DB=4m.
A
B
C
D
┌
4m
35°
40°
答:调整后的楼梯会加长约0.48m.
(2)如图,根据题意可知,∠A=35°,∠BDC=40°,DB=4m.
答:楼梯多占约0.61m长的一段地面.
A
B
C
D
┌
4m
35°
40°
如图,一灯柱AB被一钢缆CD固定.CD与地面成40°夹角,且DB=5m.现再在C点上方2m处加固另一条钢缆ED,那么,钢缆ED的长度为多少 (结果精确到0.01m).
探究四
解:如图,根据题意可知,∠CDB=40°,EC=2m,DB=5m.
∴∠BDE≈51.12°.
E
B
C
D
2 m
40°
5 m
答:钢缆ED的长度约为7.97m.
如图,水库大坝的截面是梯形ABCD,其中AD∥BC,坝顶AD=6 m,坡长CD=8 m.坡底BC=30m,∠ADC=135°.
(1)求∠ABC的大小(精确到1°);
(2)如果坝长100 m,那么修建这个大坝共需多少土石料(结果精确到0.01m3 ).
A
B
C
D
探究五
A
B
C
D
6m
8m
30m
135°
解:(1)过点D作DE⊥BC于点E,过点A作AF⊥BC于点F.
E
┐
F
┌
∴∠ABC≈17°.
答:∠ABC约为17°.
活动一 测量倾斜角(仰角或俯角)
测量倾斜角可以用测倾器,简单的测倾器由度盘、铅锤和支杆组成(如图).
30°
0°
60°
90°
90°
60°
30°
30°
0°
60°
90°
90°
60°
30°
30°
0°
60°
90°
90°
60°
30°
M
水平线
1.把支杆竖直插入地面,使支杆的中心线.铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
2.转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数.
使用测倾器测量倾斜角的步骤如下:
P
Q
活动二 测量底部可以到达的物体的高度.
所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离.
如图,要测量物体MN的高度,
1.在测点A处安置测倾器,
测得M的仰角∠MCE=α.
2.量出测点A到物体底部N的水平距离AN=l.
3.量出测倾器的高度AC=a(即顶线PQ成水平位置时,它与地面的距离).
C
A
E
N
M
可按下列步骤进行:
测量底部可以直接到达的物体的高度
在观测点A安置测倾器,测得M的仰角∠MCE=α
量出观测点A到物体底部N的水平距离AN=L
量出测倾器的高度AC=a,可求出MN的高度.MN=ME+EN=L·tanα+α
A
N
C
M
E
α
L
a
根据刚才测量的数据,你能求出物体MN的高度吗 说说你的理由.
和同伴交流一下你的发现.
在Rt△MCE中,
ME=EC·tanα=AN·tanα=l·tanα
MN=ME+EN=ME+AC=l·tanα+ a
a
C
A
E
N
M
l
α
议一议
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体的底部之间的距离.
要测量物体MN的高度,使用测倾器测一次仰角够吗?
a
α
E
C
A
N
M
活动三 测量底部不可以到达的物体的高度.
要测量物体MN的高度,测一次仰角是不够的.
a
b
α
E
C
A
D
B
β
N
M
还需哪些条件?测量哪些数据?
议一议
如图,要测量物体MN的高度,可以按下列步骤进行:
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α.
2.在测点A与物体之间的B处安置测倾器(A,B与N在一条直线上,且A,B之间的距离可以直接测得), 测得此时M的仰角∠MDE=β.
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.
根据测量数据,你能
求出物体MN的高度吗 说说你的理由.
测量底部不可以直接到达的物体的高度
在测点A处安置测倾器,测得此时M的仰角∠MCE=α
在测点A与物体之间B处安置测倾器,测得此时M的仰角∠MDE=β
量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.根据测量数据,可求出物体MN的高度。
A
C
B
D
M
N
E
α
β
过程:根据测量数据,物体MN的高度计算过程为:
a
b
α
E
C
A
D
B
β
N
M
在Rt△ MDE中,
ED=
在Rt△MCE中,
EC =
EC-ED= - =b
(2)
再求体积!
先算面积!
答:修建这个大坝共需土石料约1 0182.34 m3.
1.(株洲·中考)如图,孔明同学背着一桶水,从山脚A出发,沿与地面成30°角的山坡向上走,送水到山上因今年春季受旱缺水的王奶奶家(B处),AB=80米,则孔明从A到B上升的高度BC是 米.
【解析】依题意得,∠ACB=90°.所以sin A=sin 30°= ,所以BC=40(米).
30°
40
2.(衡阳·中考)为申办冬奥会,需改变哈尔滨市的交通状况.在大直街拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区,现在某工人站在离B点3米远的D处,从C点测得树的顶端A点的仰角为60°,树的底部B点的俯角为30°.
问:距离B点8米远的保护物是否在危险区内?
【解析】在Rt△BDC中,BC=
=2
所以离B点8米远的保护物不在危险区内.
在Rt△ABC中,AB=2BC=4
<8,
3.(湘潭·中考)如图,我护航军舰在某海域航行到B处时,灯塔A在我军舰的北偏东60o的方向;我军舰从B处向正东方向行驶1 800米到达C处,此时灯塔A在我军舰的正北方向.求C处与灯塔A的距离(结果精确到(1米)).
东
北
60o
A
C
B
【解析】在Rt△ABC中,∠C=90°,BC=1 800,∠ABC=30°,
答:C处与灯塔A的距离约为1 039米.
从而
=600
≈1 039(米).
4.(贵阳·中考)某商场为缓解我市“停车难”问题,拟建造地下停车库,如图是该地下停车库坡道入口的设计示意图,其中, AB⊥BD,∠BAD=18°,点C在BD上,BC=0.5 m.根据规定,地下停车库坡道入口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.小明认为CD的长就是所限制的高度,而小亮认为应该以CE的长作为限制的高度.小明和小亮谁说的对?请你判断并计算出正确的结果.(结果精确到0.1m)
【解析】小亮说的对,在△ABD中,∠ABD=90°,
∠BAD=18 °, BA=10 m,
∴tan∠BAD=
∴BD=10×tan 18°,
在Rt△CDE中,∠CDE=90 °
―∠BAD=72°,
∵CE⊥ED∴sin∠CDE=
∴CD=BD―BC=10×tan 18°
―0.5,
―0.5)≈2.6(m)
∴CE=CD×sin∠CDE
=sin72
°×(10×tan 18°
即限制高度为2.6 m.
【规律方法】根据题意画出几何图形,构造直角三角形,灵活运用三角函数的定义结合勾股定理的有关知识是进行解题的关键.
实际问题
图形分析
生活问题数学化
(构造直角三角形)
设未知量
解答问题
(构建三角函数模型)
(代入数据求解)
求解方程
数学问题
建立方程
B
C
600
20
450
D
┐
C
B
A
D
20
┌
300
450
┌
600
450
A
B
C
20
D
┌
300
600
A
B
C
D
20
450
300
B
C
20
A
┌
D
A
测量底部可以到达的
物体的高度,如下图
测量底部不可以直接到达的物体的高度,如下图
1.(宿迁·中考)如图,在Rt△ABC中,∠C=90°, AM是BC边上的中线, 则tan B的值为_____.
2.(孝感·中考)如图,一艘船向正北航行,在A处看到灯塔S在船的北偏东30°的方向上,航行12海里到达B点,在B处看到灯塔S在船的北偏东60°的方向上,此船继续沿正北方向航行过程中距灯塔S的最近距离是_____海里(不作近似计算).
3.(呼和浩特·中考)如图,在△ABC中,∠C=90°,∠B=30°,AD是∠BAC的角平分线,与BC相交于点D,且AB=4 ,求AD的长.
∵ AD平分∠BAC,
【解析】在Rt△ABC中,
AB=
×4
∴ AC=
=
=4.
∴ AD=
∴ 在Rt△ACD中,∠CAD=30°.
∵ ∠B=30°,
4.小明家所在居民楼的对面有一座大厦AB,AB=80米.为测量居民楼与这座大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.(结果保留整数)
(参考数据: )
∵AD+BD = AB,∴
【解析】设CD =x 米.在Rt△ACD中,
在Rt△BCD,tan48°=
解得:x≈43.
答:小明家所在居民楼与大厦的距离CD大约是43米.
则
则
