人教版数学九年级上册 21.2 解一元二次方程 课件(共29张PPT)
文档属性
| 名称 | 人教版数学九年级上册 21.2 解一元二次方程 课件(共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-21 13:21:10 | ||
图片预览





文档简介
(共30张PPT)
21.2 解一元二次方程
学习目标: 1.会用直接开平方法解一元二次方程,理解配方的 基本过程,会用配方法解一元二次方程; 2.会用公式法解一元二次方程,理解用根的判别式 判别根的情况; 3.会选择合适的方法进行因式分解,并解一元二次方程;
学习重点: 解一元二次方程.
问题1 在设计人体雕像时,使雕像的上部(腰以 上)与下部(腰以下)的高度比,等于下部与全部(全 身)的高度比,可以增加视觉美感.按此比例,如果雕 像的高为 2 m,那么它的下部应设计为多高?
解:设雕像的下部高为 x m,
据题意,列方程得
整理得 x 2 + 2x - 4 = 0.
A
C
B
1.创设情境,导入新知
x 2 = 2 2 - x ,
( )
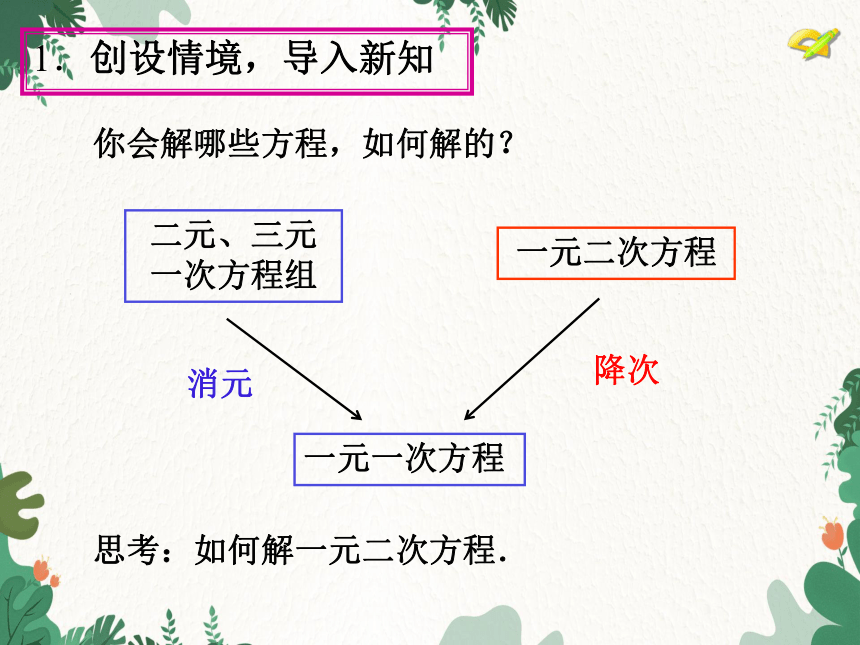
你会解哪些方程,如何解的?
二元、三元一次方程组
一元一次方程
一元二次方程
消元
降次
思考:如何解一元二次方程.
1.创设情境,导入新知
问题2 解方程 x 2 = 25,依据是什么?
解得 x 1 = 5,x 2 = - 5.
平方根的意义
请解下列方程: x 2 = 3,2x 2 - 8=0,x 2 = 0,x 2 = - 2… 这些方程有什么共同的特征?
结构特征:方程可化成 x 2 = p 的形式,
平方根的意义
降次
(当 p≥0 时)
问题3 解方程:(x + 3)= 5.
2
2.推导求根公式
问题4 怎样解方程 x 2 + 6x + 4 = 0 ①?
x 2 + 6x + 9 = 5 ②
(x + 3)= 5
2
2.推导求根公式
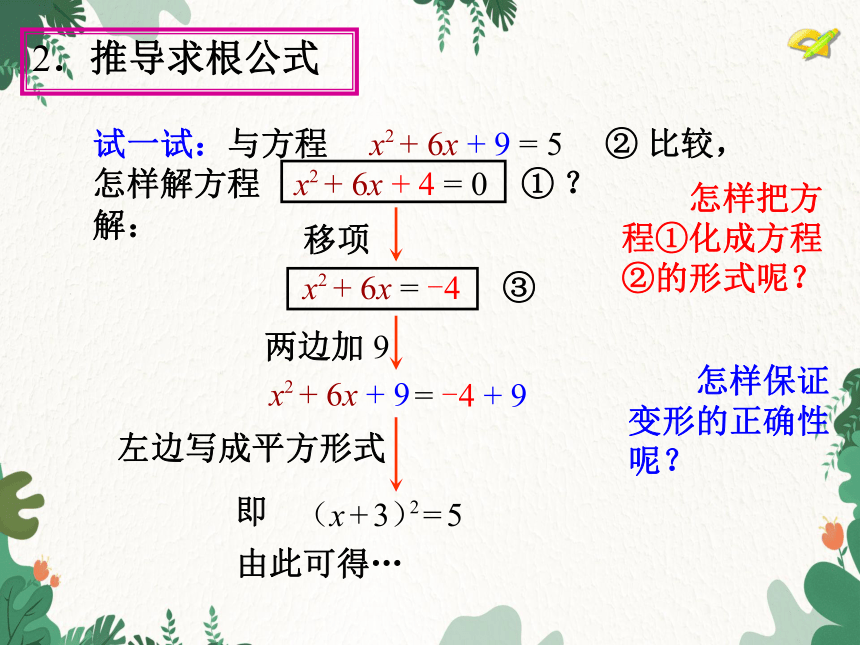
试一试:与方程 x2 + 6x + 9 = 5 ② 比较,
怎样解方程 x2 + 6x + 4 = 0 ① ?
怎样把方程①化成方程②的形式呢?
怎样保证变形的正确性呢?
即
由此可得…
解:
左边写成平方形式
移项
x2 + 6x = -4 ③
两边加 9
= -4 + 9
x2 + 6x + 9
2.推导求根公式
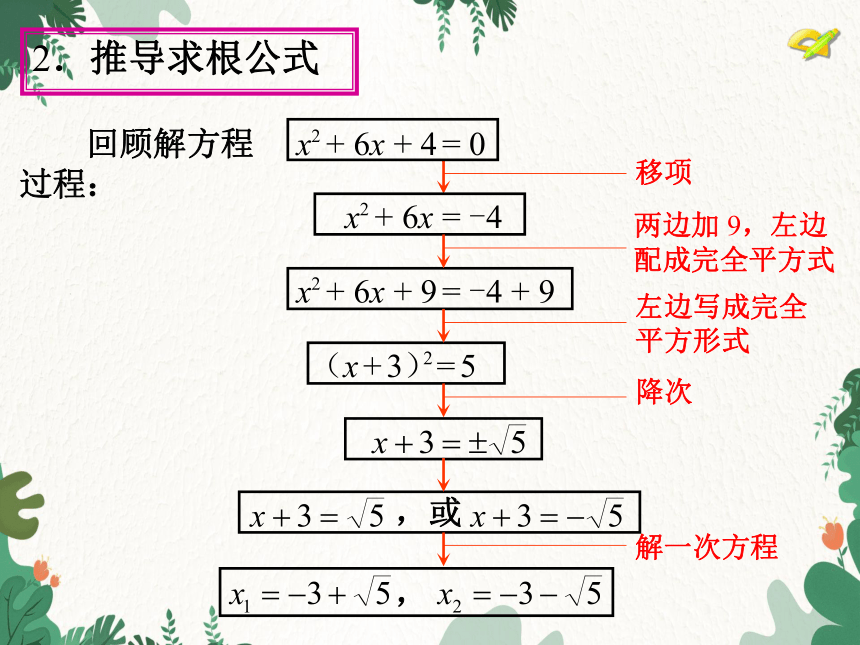
(x + 3)= 5
2
回顾解方程过程:
两边加 9,左边 配成完全平方式
移项
左边写成完全 平方形式
降次
解一次方程
x2 + 6x + 4 = 0
x2 + 6x = -4
x2 + 6x + 9 = -4 + 9
,或
,
2.推导求根公式
(x + 3)= 5
2
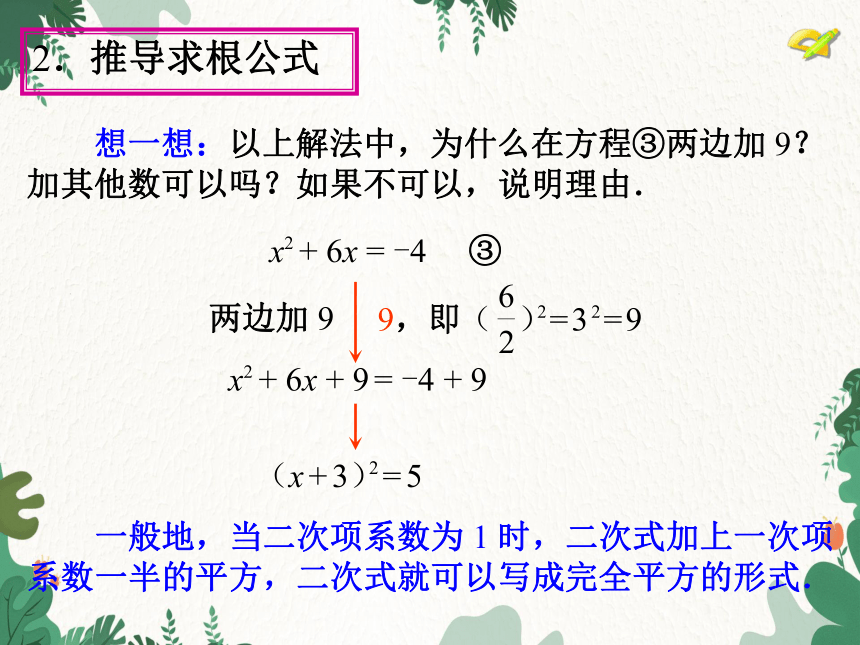
想一想:以上解法中,为什么在方程③两边加 9? 加其他数可以吗?如果不可以,说明理由.
两边加 9
一般地,当二次项系数为 1 时,二次式加上一次项系数一半的平方,二次式就可以写成完全平方的形式.
x2 + 6x = -4 ③
x2 + 6x + 9 = -4 + 9
2.推导求根公式
(x + 3)= 5
2
9,即 2 = 3 2 = 9
( )
议一议:结合方程①的解答过程,说出解一般二次 项系数为 1 的一元二次方程的基本思路是什么?具体步 骤是什么?
配成完全平方形式
通过 来解一元二次方程的方法, 叫做配方法.
配方
具体步骤:
(1)移项;
(2)在方程两边都加上一次项系数一半的平方.
2.推导求根公式
平方根的意义
降次
(当 p≥0 时)
问题5 通过解方程 x 2 + 6x + 4=0 ,请归纳这类方程是怎样解的?
3.归纳配方法解方程的步骤
结构特征:方程可化成 的形式,
(x + n)= p
2
(2)配方法解一元二次方程的一般步骤有哪些
3.归纳配方法解方程的步骤
(1)用配方法解一元二次方程的基本思路是什么? 把方程配方为 的形式,运用开平方法, 降次求解.
(x + n)= p
2
解一元二次方程的一般步骤:
两边加 9,左边 配成完全平方式
移项
左边写成完全 平方形式
降次
x2 + 6x + 4 = 0
x2 + 6x = -4
x2 + 6x + 9 = -4 + 9
,或
3.归纳配方法解方程的步骤
(x + 3)= 5
2
解一次方程
,
4.归纳小结
(2)配方法解一元二次方程的一般步骤有哪些
(3)在配方法解一元二次方程的过程中应该注意 哪些问题
(1)用配方法解一元二次方程的基本思路是什么? 把方程配方为 的形式,运用开平方法, 降次求解.
(x + n)= p
2
1.复习配方法,引入公式法
问题1 什么叫配方法?配方法的基本步骤是什么?
(1)将方程二次项系数化成 1;
(2)移项;
(3)配方;
(4)化为(x + n)= p(n,p 是常数,p≥0)的形 式;
(5)用直接开平方法求得方程的解.
2
问题2 能否用公式法解决一元二次方程的求根问 题呢?
问题3 我们知道,任意一个一元二次方程都可以 转化为一般形式
ax 2 + bx + c = 0 (a≠0)
你能用配方法得出它的解吗?
2.推导求根公式
此时可以用开平方法求解吗?
2.推导求根公式
一般地,一元二次方程 ax 2 + bx + c = 0(a≠0)的根 由方程的系数 a,b,c 确定.将 a,b,c 代入式子就得 到方程的根:
利用它解一元二次方程的方法叫做公式法.
2.推导求根公式
你能总结一下推导求根公式的基本步骤吗?推导过 程中要注意那些问题?
当 时,方程有两个不相等的实根; 当 时,方程有两个相等的实根; 当 时,方程没有实根.
2.推导求根公式
b 2 - 4ac>0
b 2 - 4ac = 0
b 2 - 4ac<0
例1 用公式法解下列方程: (1) x 2 - 4x - 7 = 0; (2) ;
(3)5x 2 - 3x = x + 1;
(4)x 2 + 17 = 8x.
3.归纳公式法解方程的步骤
问题4:你能总结用公式法解一元二次方程的步骤 吗?应用公式时要注意什么问题?
3.归纳公式法解方程的步骤
回到本章引言中的问题,雕像下部高度 x(m)满 足方程
x 2 + 2x - 4 = 0.
用公式法解这个方程:
4.练习巩固公式法
(1)如果雕像的高度设计为 3 m,那雕像的下部 应是多少?4 m 呢?
(2)进而把问题一般化,这个高度比是多少?
问题5:请大家思考并回答以下问题:
(1)本节课学了哪些内容?
(2)我们是用什么方法推导求根公式的?
(3)你认为判别式有哪些作用?
(4)应用公式法解一元二次方程的步骤是什么?
5.归纳小结
问题1 根据物理学规律,如果把一个物体从地面 以 10 m/s 的速度竖直上抛,那么经过 x s 物体离地面的 高度(单位:m)为
10x - 4.9x 2.
你能根据上述规律求出物体经过多少秒落回地面吗(精确到 0.01 s)?
1.探究因式分解法
你认为该如何解决这个问题?你想用哪种方法解这 个方程?
配方法
公式法
降次
?
1.探究因式分解法
10x - 4.9x 2 = 0
x 1 = 0,x 2 =
问题3 观察方程 10x - 4.9x 2 = 0,它有什么特点? 你能根据它的特点找到更简便的方法吗?
两个因式的积等于零
至少有一个因式为零
1.探究因式分解法
10x - 4.9x 2 = 0
x 1 = 0,x 2 =
x = 0
或 10 - 4.9x = 0
x 10 - 4.9x = 0
( )
例 解下列方程: (1)
(2)
2.应用举例
归纳因式分解法解一元二次方程的步骤:
(1)化方程为一般形式;
(2)将方程左边因式分解;
(3)至少有一个因式为零,得到两个一元一次方 程;
(4)两个一元一次方程的解就是原方程的解.
x x - 2 + x - 2 = 0
( )
问题4 请回答以下问题:
(1)因式分解法的依据是什么?解题步骤是什么?
(2)回顾配方法、公式法和因式分解法,你能说 出它们各自的特点吗?
4.归纳小结
教科书习题 21.2
5.布置作业
21.2 解一元二次方程
学习目标: 1.会用直接开平方法解一元二次方程,理解配方的 基本过程,会用配方法解一元二次方程; 2.会用公式法解一元二次方程,理解用根的判别式 判别根的情况; 3.会选择合适的方法进行因式分解,并解一元二次方程;
学习重点: 解一元二次方程.
问题1 在设计人体雕像时,使雕像的上部(腰以 上)与下部(腰以下)的高度比,等于下部与全部(全 身)的高度比,可以增加视觉美感.按此比例,如果雕 像的高为 2 m,那么它的下部应设计为多高?
解:设雕像的下部高为 x m,
据题意,列方程得
整理得 x 2 + 2x - 4 = 0.
A
C
B
1.创设情境,导入新知
x 2 = 2 2 - x ,
( )
你会解哪些方程,如何解的?
二元、三元一次方程组
一元一次方程
一元二次方程
消元
降次
思考:如何解一元二次方程.
1.创设情境,导入新知
问题2 解方程 x 2 = 25,依据是什么?
解得 x 1 = 5,x 2 = - 5.
平方根的意义
请解下列方程: x 2 = 3,2x 2 - 8=0,x 2 = 0,x 2 = - 2… 这些方程有什么共同的特征?
结构特征:方程可化成 x 2 = p 的形式,
平方根的意义
降次
(当 p≥0 时)
问题3 解方程:(x + 3)= 5.
2
2.推导求根公式
问题4 怎样解方程 x 2 + 6x + 4 = 0 ①?
x 2 + 6x + 9 = 5 ②
(x + 3)= 5
2
2.推导求根公式
试一试:与方程 x2 + 6x + 9 = 5 ② 比较,
怎样解方程 x2 + 6x + 4 = 0 ① ?
怎样把方程①化成方程②的形式呢?
怎样保证变形的正确性呢?
即
由此可得…
解:
左边写成平方形式
移项
x2 + 6x = -4 ③
两边加 9
= -4 + 9
x2 + 6x + 9
2.推导求根公式
(x + 3)= 5
2
回顾解方程过程:
两边加 9,左边 配成完全平方式
移项
左边写成完全 平方形式
降次
解一次方程
x2 + 6x + 4 = 0
x2 + 6x = -4
x2 + 6x + 9 = -4 + 9
,或
,
2.推导求根公式
(x + 3)= 5
2
想一想:以上解法中,为什么在方程③两边加 9? 加其他数可以吗?如果不可以,说明理由.
两边加 9
一般地,当二次项系数为 1 时,二次式加上一次项系数一半的平方,二次式就可以写成完全平方的形式.
x2 + 6x = -4 ③
x2 + 6x + 9 = -4 + 9
2.推导求根公式
(x + 3)= 5
2
9,即 2 = 3 2 = 9
( )
议一议:结合方程①的解答过程,说出解一般二次 项系数为 1 的一元二次方程的基本思路是什么?具体步 骤是什么?
配成完全平方形式
通过 来解一元二次方程的方法, 叫做配方法.
配方
具体步骤:
(1)移项;
(2)在方程两边都加上一次项系数一半的平方.
2.推导求根公式
平方根的意义
降次
(当 p≥0 时)
问题5 通过解方程 x 2 + 6x + 4=0 ,请归纳这类方程是怎样解的?
3.归纳配方法解方程的步骤
结构特征:方程可化成 的形式,
(x + n)= p
2
(2)配方法解一元二次方程的一般步骤有哪些
3.归纳配方法解方程的步骤
(1)用配方法解一元二次方程的基本思路是什么? 把方程配方为 的形式,运用开平方法, 降次求解.
(x + n)= p
2
解一元二次方程的一般步骤:
两边加 9,左边 配成完全平方式
移项
左边写成完全 平方形式
降次
x2 + 6x + 4 = 0
x2 + 6x = -4
x2 + 6x + 9 = -4 + 9
,或
3.归纳配方法解方程的步骤
(x + 3)= 5
2
解一次方程
,
4.归纳小结
(2)配方法解一元二次方程的一般步骤有哪些
(3)在配方法解一元二次方程的过程中应该注意 哪些问题
(1)用配方法解一元二次方程的基本思路是什么? 把方程配方为 的形式,运用开平方法, 降次求解.
(x + n)= p
2
1.复习配方法,引入公式法
问题1 什么叫配方法?配方法的基本步骤是什么?
(1)将方程二次项系数化成 1;
(2)移项;
(3)配方;
(4)化为(x + n)= p(n,p 是常数,p≥0)的形 式;
(5)用直接开平方法求得方程的解.
2
问题2 能否用公式法解决一元二次方程的求根问 题呢?
问题3 我们知道,任意一个一元二次方程都可以 转化为一般形式
ax 2 + bx + c = 0 (a≠0)
你能用配方法得出它的解吗?
2.推导求根公式
此时可以用开平方法求解吗?
2.推导求根公式
一般地,一元二次方程 ax 2 + bx + c = 0(a≠0)的根 由方程的系数 a,b,c 确定.将 a,b,c 代入式子就得 到方程的根:
利用它解一元二次方程的方法叫做公式法.
2.推导求根公式
你能总结一下推导求根公式的基本步骤吗?推导过 程中要注意那些问题?
当 时,方程有两个不相等的实根; 当 时,方程有两个相等的实根; 当 时,方程没有实根.
2.推导求根公式
b 2 - 4ac>0
b 2 - 4ac = 0
b 2 - 4ac<0
例1 用公式法解下列方程: (1) x 2 - 4x - 7 = 0; (2) ;
(3)5x 2 - 3x = x + 1;
(4)x 2 + 17 = 8x.
3.归纳公式法解方程的步骤
问题4:你能总结用公式法解一元二次方程的步骤 吗?应用公式时要注意什么问题?
3.归纳公式法解方程的步骤
回到本章引言中的问题,雕像下部高度 x(m)满 足方程
x 2 + 2x - 4 = 0.
用公式法解这个方程:
4.练习巩固公式法
(1)如果雕像的高度设计为 3 m,那雕像的下部 应是多少?4 m 呢?
(2)进而把问题一般化,这个高度比是多少?
问题5:请大家思考并回答以下问题:
(1)本节课学了哪些内容?
(2)我们是用什么方法推导求根公式的?
(3)你认为判别式有哪些作用?
(4)应用公式法解一元二次方程的步骤是什么?
5.归纳小结
问题1 根据物理学规律,如果把一个物体从地面 以 10 m/s 的速度竖直上抛,那么经过 x s 物体离地面的 高度(单位:m)为
10x - 4.9x 2.
你能根据上述规律求出物体经过多少秒落回地面吗(精确到 0.01 s)?
1.探究因式分解法
你认为该如何解决这个问题?你想用哪种方法解这 个方程?
配方法
公式法
降次
?
1.探究因式分解法
10x - 4.9x 2 = 0
x 1 = 0,x 2 =
问题3 观察方程 10x - 4.9x 2 = 0,它有什么特点? 你能根据它的特点找到更简便的方法吗?
两个因式的积等于零
至少有一个因式为零
1.探究因式分解法
10x - 4.9x 2 = 0
x 1 = 0,x 2 =
x = 0
或 10 - 4.9x = 0
x 10 - 4.9x = 0
( )
例 解下列方程: (1)
(2)
2.应用举例
归纳因式分解法解一元二次方程的步骤:
(1)化方程为一般形式;
(2)将方程左边因式分解;
(3)至少有一个因式为零,得到两个一元一次方 程;
(4)两个一元一次方程的解就是原方程的解.
x x - 2 + x - 2 = 0
( )
问题4 请回答以下问题:
(1)因式分解法的依据是什么?解题步骤是什么?
(2)回顾配方法、公式法和因式分解法,你能说 出它们各自的特点吗?
4.归纳小结
教科书习题 21.2
5.布置作业
同课章节目录
