苏教版必修第二册 第14章 统计 章末检测试卷(Word版含解析)
文档属性
| 名称 | 苏教版必修第二册 第14章 统计 章末检测试卷(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 553.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-20 08:54:13 | ||
图片预览


文档简介
章末检测试卷六(第14章)
(时间:120分钟 满分:150分)
一、单项选择题(本大题共8小题,每小题5分,共40分)
1.为了了解所加工的一批零件的长度,抽测了其中200个零件的长度,在这个问题中,200个零件的长度是( )
A.总体 B.个体
C.总体的一个样本 D.样本容量
2.①一次数学考试中,某班有10人的成绩在100分以上,32人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人了解有关情况;②运动会的工作人员为参加4×100 m接力赛的6支队伍安排跑道.针对这两件事,恰当的抽样方法分别为( )
A.分层抽样,简单随机抽样
B.简单随机抽样,简单随机抽样
C.简单随机抽样,分层抽样
D.分层抽样,分层抽样
3.为了调查学生每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.样本容量为1 000的频率直方图如图所示,则样本数据落在[6,14)内的频数为( )
A.780 B.680 C.648 D.460
4.某校高二年级有50人参加2021“希望杯”数学竞赛,他们竞赛的成绩制成了如下的频率分布表,根据该表估计该校学生数学竞赛成绩的平均分为( )
分组 [60,70) [70,80) [80,90) [90,100]
频率 0.2 0.4 0.3 0.1
A.70 B.73 C.78 D.81.5
5.我国古代数学专著《九章算术》中有一衰分问题:今有北乡八千一百人,西乡七千四百八十八人,南乡六千九百一十二人,凡三乡,发役三百人,则北乡遣( )
A.104人 B.108人 C.112人 D.120人
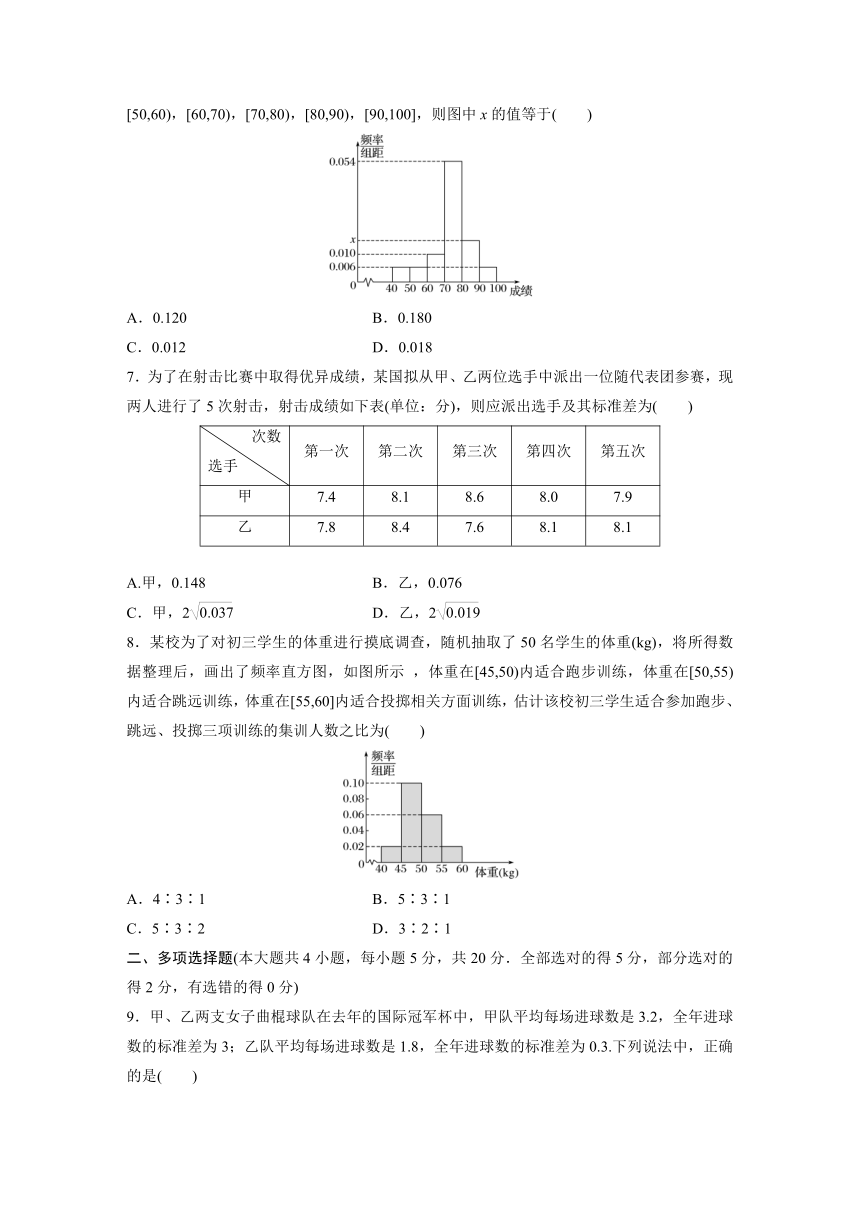
6.如图是某班50名学生期中考试数学成绩的频率直方图,其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],则图中x的值等于( )
A.0.120 B.0.180
C.0.012 D.0.018
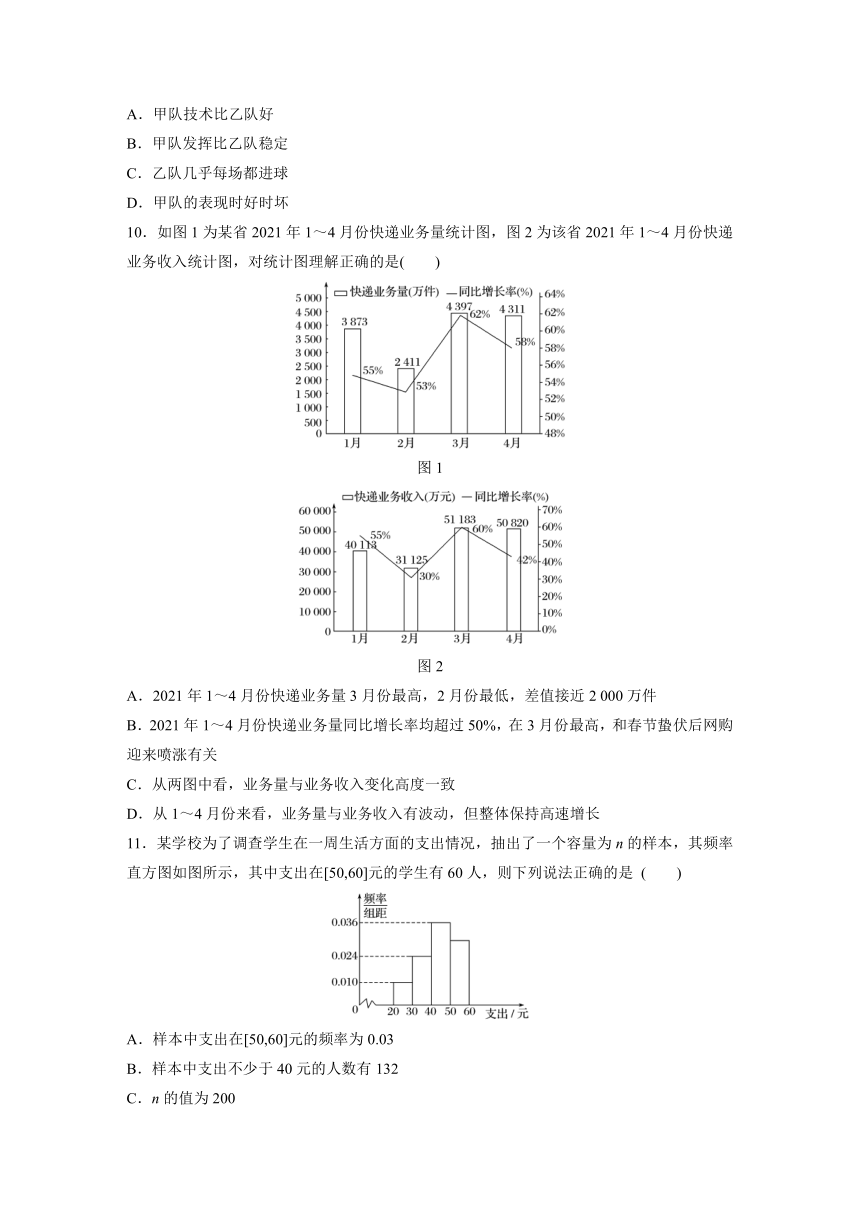
7.为了在射击比赛中取得优异成绩,某国拟从甲、乙两位选手中派出一位随代表团参赛,现两人进行了5次射击,射击成绩如下表(单位:分),则应派出选手及其标准差为( )
次数 选手 第一次 第二次 第三次 第四次 第五次
甲 7.4 8.1 8.6 8.0 7.9
乙 7.8 8.4 7.6 8.1 8.1
A.甲,0.148 B.乙,0.076
C.甲,2 D.乙,2
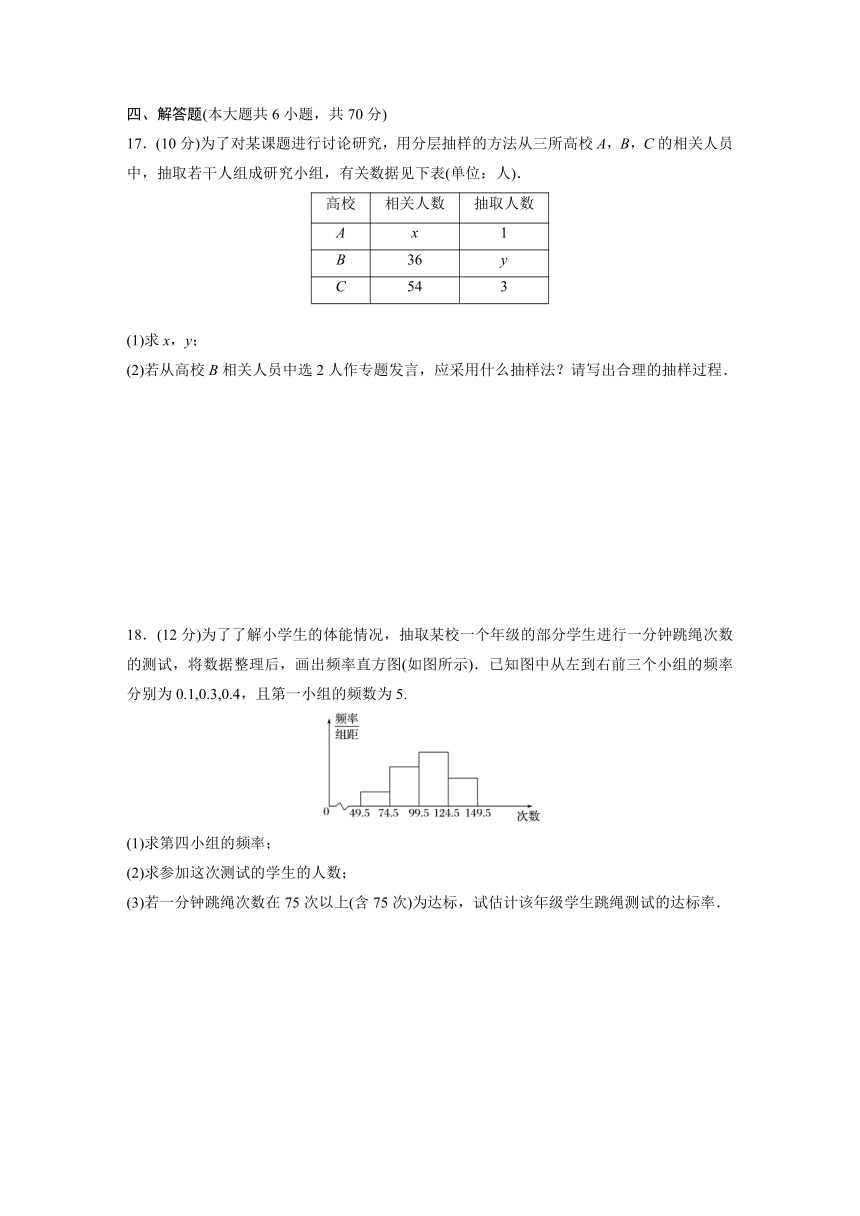
8.某校为了对初三学生的体重进行摸底调查,随机抽取了50名学生的体重(kg),将所得数据整理后,画出了频率直方图,如图所示 ,体重在[45,50)内适合跑步训练,体重在[50,55)内适合跳远训练,体重在[55,60]内适合投掷相关方面训练,估计该校初三学生适合参加跑步、跳远、投掷三项训练的集训人数之比为( )
A.4∶3∶1 B.5∶3∶1
C.5∶3∶2 D.3∶2∶1
二、多项选择题(本大题共4小题,每小题5分,共20分.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.甲、乙两支女子曲棍球队在去年的国际冠军杯中,甲队平均每场进球数是3.2,全年进球数的标准差为3;乙队平均每场进球数是1.8,全年进球数的标准差为0.3.下列说法中,正确的是( )
A.甲队技术比乙队好
B.甲队发挥比乙队稳定
C.乙队几乎每场都进球
D.甲队的表现时好时坏
10.如图1为某省2021年1~4月份快递业务量统计图,图2为该省2021年1~4月份快递业务收入统计图,对统计图理解正确的是( )
图1
图2
A.2021年1~4月份快递业务量3月份最高,2月份最低,差值接近2 000万件
B.2021年1~4月份快递业务量同比增长率均超过50%,在3月份最高,和春节蛰伏后网购迎来喷涨有关
C.从两图中看,业务量与业务收入变化高度一致
D.从1~4月份来看,业务量与业务收入有波动,但整体保持高速增长
11.某学校为了调查学生在一周生活方面的支出情况,抽出了一个容量为n的样本,其频率直方图如图所示,其中支出在[50,60]元的学生有60人,则下列说法正确的是 ( )
A.样本中支出在[50,60]元的频率为0.03
B.样本中支出不少于40元的人数有132
C.n的值为200
D.若该校有2 000名学生,则一定有600人支出在[50,60]元
12.某赛季甲、乙两名篮球运动员各6场比赛得分情况记录如下,
甲:18,20,35,33,47,41;
乙:17,26,19,27,19,29.
则下列四个结论中,正确的是( )
A.甲运动员得分的极差大于乙运动员得分的极差
B.甲运动员得分的中位数大于乙运动员得分的中位数
C.甲运动员得分的平均数大于乙运动员得分的平均数
D.甲运动员的成绩比乙运动员的成绩稳定
三、填空题(本大题共4小题,每小题5分,共20分)
13.一个总体容量为60,其中的个体编号为00,01,02,…,59.现需从中抽取一个容量为7的样本,请从随机数表的倒数第5行(下表为随机数表的最后5行)第11~12列的18开始,依次向下,到最后一行后向右,直到取足样本,则抽取样本的号码是________.
95 33 95 22 00 18 74 72 00 18 46 40 62 98 80 54 97 20 56 95
38 79 58 69 32 81 76 80 26 92 15 74 80 08 32 16 46 70 50 80
82 80 84 25 39 90 84 60 79 80 67 72 16 42 79 71 59 73 05 50
24 36 59 87 38 82 07 53 89 35 08 22 23 71 77 91 01 93 20 49
96 35 23 79 18 05 98 90 07 35 82 96 59 26 94 66 39 67 98 60
14.如图所示是一次考试结果的频率直方图,则据此估计这次考试的平均分为________分.
15.数据3.2,3.6,4.5,2.4,4.6,6.4,7.8,7.9,8.0,8.1,8.4,8.6的50百分位数是________,75百分位数是________.
16.学校开展“书香校园”活动以来,受到同学们的广泛关注.学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计图表.
若该组数的平均数、众数、中位数依次为a,b,c,则a,b,c的大小关系为________.
四、解答题(本大题共6小题,共70分)
17.(10分)为了对某课题进行讨论研究,用分层抽样的方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人).
高校 相关人数 抽取人数
A x 1
B 36 y
C 54 3
(1)求x,y;
(2)若从高校B相关人员中选2人作专题发言,应采用什么抽样法?请写出合理的抽样过程.
18.(12分)为了了解小学生的体能情况,抽取某校一个年级的部分学生进行一分钟跳绳次数的测试,将数据整理后,画出频率直方图(如图所示).已知图中从左到右前三个小组的频率分别为0.1,0.3,0.4,且第一小组的频数为5.
(1)求第四小组的频率;
(2)求参加这次测试的学生的人数;
(3)若一分钟跳绳次数在75次以上(含75次)为达标,试估计该年级学生跳绳测试的达标率.
19.(12分)某公司共有员工120人,用简单随机抽样任意抽取12人,得到这12人的月工资(单位:千元)如下:
7.5,6.8,8.6,6.2,7.8,8.9,7.8,8.0,8.5,8.2,7.2,8.0,试估计该公司员工工资的25,50,90百分位数.
20.(12分)甲、乙两位同学进行投篮比赛,每人玩5局,每局在指定线外投篮,若第一次不进,再投第二次,依此类推,但最多只能投6次.当投进时,该局结束,并记下投篮的次数.当6次投不进,该局也结束,记为“×”.第一次投进得6分,第二次投进得5分,第三次投进得4分,依此类推,第6次投不进,得0分.两人的投篮情况如下:
第1局 第2局 第3局 第4局 第5局
甲 5次 × 4次 5次 1次
乙 × 2次 4次 2次 ×
请通过计算,判断哪位同学投篮的水平高.
21.(12分)为了了解某市参加2021年全国高中数学联赛的学生考试结果情况,从中选取60名同学将其成绩(百分制,均为正数)分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组后,得到部分频率直方图(如图),观察图形,回答下列问题:
(1)求分数在[70,80)内的频率,并补全这个频率直方图;
(2)根据频率直方图,估计本次考试成绩的众数、平均数;
(3)根据评奖规则,排名靠前10%的同学可以获奖,请你估计获奖的同学至少需要多少分?
22.(12分)某初级中学共有学生2 000名,各年级男、女生人数如下表:
初一年级 初二年级 初三年级
女生 373 x y
男生 377 370 z
已知在全校学生中随机抽取1名,抽到初二年级女生的频率是0.19.
(1)求x的值;
(2)现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
(3)在(2)中,若所抽取的初一年级、初二年级、初三年级三个年级学生的体重的平均数分别是40 kg,50 kg,60 kg,方差分别是1,2,3,估计该校所有学生体重的平均数和方差.
章末检测试卷六(第14章)
(时间:120分钟 满分:150分)
一、单项选择题(本大题共8小题,每小题5分,共40分)
1.为了了解所加工的一批零件的长度,抽测了其中200个零件的长度,在这个问题中,200个零件的长度是( )
A.总体 B.个体
C.总体的一个样本 D.样本容量
答案 C
解析 总体是这批零件的长度,个体是这批零件中每个零件的长度,样本是抽取的200个零件的长度,样本容量是200.
2.①一次数学考试中,某班有10人的成绩在100分以上,32人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人了解有关情况;②运动会的工作人员为参加4×100 m接力赛的6支队伍安排跑道.针对这两件事,恰当的抽样方法分别为( )
A.分层抽样,简单随机抽样
B.简单随机抽样,简单随机抽样
C.简单随机抽样,分层抽样
D.分层抽样,分层抽样
答案 A
解析 ①中,考试成绩在不同分数段之间的同学有明显的差异,用分层抽样比较恰当;②中,总体包含的个体较少,用简单随机抽样比较恰当.
3.为了调查学生每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.样本容量为1 000的频率直方图如图所示,则样本数据落在[6,14)内的频数为( )
A.780 B.680 C.648 D.460
答案 B
解析 频率直方图中每个小长方形的面积就是相应的频率,所以1 000-(0.02×4+0.03×4×2)×1 000=680.
4.某校高二年级有50人参加2021“希望杯”数学竞赛,他们竞赛的成绩制成了如下的频率分布表,根据该表估计该校学生数学竞赛成绩的平均分为( )
分组 [60,70) [70,80) [80,90) [90,100]
频率 0.2 0.4 0.3 0.1
A.70 B.73 C.78 D.81.5
答案 C
解析 估计该校学生数学竞赛成绩的平均分=65×0.2+75×0.4+85×0.3+95×0.1=78,故选C.
5.我国古代数学专著《九章算术》中有一衰分问题:今有北乡八千一百人,西乡七千四百八十八人,南乡六千九百一十二人,凡三乡,发役三百人,则北乡遣( )
A.104人 B.108人 C.112人 D.120人
答案 B
解析 由题意可知,这是一个分层抽样的问题,其中北乡可抽取的人数为300×=300×=108,故选B.
6.如图是某班50名学生期中考试数学成绩的频率直方图,其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],则图中x的值等于( )
A.0.120 B.0.180
C.0.012 D.0.018
答案 D
解析 由题图可知纵坐标表示.
故x=0.1-0.054-0.010-0.006-0.006-0.006=0.018.
7.为了在射击比赛中取得优异成绩,某国拟从甲、乙两位选手中派出一位随代表团参赛,现两人进行了5次射击,射击成绩如下表(单位:分),则应派出选手及其标准差为( )
次数 选手 第一次 第二次 第三次 第四次 第五次
甲 7.4 8.1 8.6 8.0 7.9
乙 7.8 8.4 7.6 8.1 8.1
A.甲,0.148 B.乙,0.076
C.甲,2 D.乙,2
答案 D
解析 甲选手成绩的平均数为=8.0,
方差为[(7.4-8)2+(8.1-8)2+(8.6-8)2+(8-8)2+(7.9-8)2]=0.148,
乙选手成绩的平均数为=8.0,
方差为[(7.8-8)2+(8.4-8)2+(7.6-8)2+(8.1-8)2+(8.1-8)2]=0.076,
甲、乙成绩的平均数相同,但乙方差较小,故乙的成绩较稳定,
应选乙,其标准差为=2,故选D.
8.某校为了对初三学生的体重进行摸底调查,随机抽取了50名学生的体重(kg),将所得数据整理后,画出了频率直方图,如图所示 ,体重在[45,50)内适合跑步训练,体重在[50,55)内适合跳远训练,体重在[55,60]内适合投掷相关方面训练,估计该校初三学生适合参加跑步、跳远、投掷三项训练的集训人数之比为( )
A.4∶3∶1 B.5∶3∶1
C.5∶3∶2 D.3∶2∶1
答案 B
解析 体重在[45,50)内的频率为0.1×5=0.5,体重在[50,55)内的频率为0.06×5=0.3,体重在[55,60]内的频率为0.02×5=0.1,
∵0.5∶0.3∶0.1=5∶3∶1,
∴可估计该校初三学生适合参加跑步、跳远、投掷三项训练的集训人数之比为5∶3∶1,故选B.
二、多项选择题(本大题共4小题,每小题5分,共20分.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.甲、乙两支女子曲棍球队在去年的国际冠军杯中,甲队平均每场进球数是3.2,全年进球数的标准差为3;乙队平均每场进球数是1.8,全年进球数的标准差为0.3.下列说法中,正确的是( )
A.甲队技术比乙队好
B.甲队发挥比乙队稳定
C.乙队几乎每场都进球
D.甲队的表现时好时坏
答案 ACD
解析 因为甲队的平均进球数比乙队多,所以甲队技术较好,A正确;乙队的标准差比甲队小,标准差越小越稳定,所以乙队发挥稳定,B错误;乙队平均每场进球数为1.8,且乙队全年进球数的标准差较小,所以乙队几乎每场都进球,C正确;由于s甲=3,s乙=0.3,所以甲队与乙队相比,不稳定,所以甲队的表现时好时坏,D正确.
10.如图1为某省2021年1~4月份快递业务量统计图,图2为该省2021年1~4月份快递业务收入统计图,对统计图理解正确的是( )
图1
图2
A.2021年1~4月份快递业务量3月份最高,2月份最低,差值接近2 000万件
B.2021年1~4月份快递业务量同比增长率均超过50%,在3月份最高,和春节蛰伏后网购迎来喷涨有关
C.从两图中看,业务量与业务收入变化高度一致
D.从1~4月份来看,业务量与业务收入有波动,但整体保持高速增长
答案 ABC
解析 由图1可知快递业务量3月份为4 397万件,2月份为2 411万件,差值为4 397-2 411=1 986(万件),故A正确;由图1可知B也正确;对于C,由两图易知业务量从高到低变化是3月→4月→1月→2月,业务收入从高到低变化是3月→4月→1月→2月,保持高度一致,所以C正确;对于D,由图知业务收入2月比1月减少,4月比3月减少,整体不具备高速增长之说,所以D不正确.
11.某学校为了调查学生在一周生活方面的支出情况,抽出了一个容量为n的样本,其频率直方图如图所示,其中支出在[50,60]元的学生有60人,则下列说法正确的是 ( )
A.样本中支出在[50,60]元的频率为0.03
B.样本中支出不少于40元的人数有132
C.n的值为200
D.若该校有2 000名学生,则一定有600人支出在[50,60]元
答案 BC
解析 由频率直方图得,
在A中,样本中支出在[50,60]元的频率为1-(0.01+0.024+0.036)×10=0.3,故A错误;
在B中,样本中支出不少于40元的人数有×0.36+60=132,故B正确;
在C中,n==200,故n的值为200,故C正确;
D.若该校有2 000名学生,则可能有600人支出在[50,60]元,故D错误.
12.某赛季甲、乙两名篮球运动员各6场比赛得分情况记录如下,
甲:18,20,35,33,47,41;
乙:17,26,19,27,19,29.
则下列四个结论中,正确的是( )
A.甲运动员得分的极差大于乙运动员得分的极差
B.甲运动员得分的中位数大于乙运动员得分的中位数
C.甲运动员得分的平均数大于乙运动员得分的平均数
D.甲运动员的成绩比乙运动员的成绩稳定
答案 ABC
解析 对于A,甲运动员得分的极差为47-18=29,乙运动员得分的极差为29-17=12,甲运动员得分的极差大于乙运动员得分的极差,因此A正确;
对于B,甲的数据从小到大排列后,处于中间的数是33,35,所以甲运动员得分的中位数是34,同理求得乙运动员得分的中位数是22.5,因此甲运动员得分的中位数大于乙运动员得分的中位数,故B正确;
对于C,甲运动员得分的平均数为≈32.33,乙运动员得分的平均数为≈22.83,因此甲运动员得分的平均数大于乙运动员得分的平均数,故C正确;
对于D,分别计算甲、乙两个运动员得分的方差,方差小的成绩更稳定.可以算出甲的方差为s≈109.22,乙的方差为s≈21.47,因为乙的方差小于甲的方差,所以乙运动员的成绩比甲运动员的成绩稳定,故D不正确.
三、填空题(本大题共4小题,每小题5分,共20分)
13.一个总体容量为60,其中的个体编号为00,01,02,…,59.现需从中抽取一个容量为7的样本,请从随机数表的倒数第5行(下表为随机数表的最后5行)第11~12列的18开始,依次向下,到最后一行后向右,直到取足样本,则抽取样本的号码是________.
95 33 95 22 00 18 74 72 00 18 46 40 62 98 80 54 97 20 56 95
38 79 58 69 32 81 76 80 26 92 15 74 80 08 32 16 46 70 50 80
82 80 84 25 39 90 84 60 79 80 67 72 16 42 79 71 59 73 05 50
24 36 59 87 38 82 07 53 89 35 08 22 23 71 77 91 01 93 20 49
96 35 23 79 18 05 98 90 07 35 82 96 59 26 94 66 39 67 98 60
答案 18,05,07,35,59,26,39.
解析 根据题意,60个个体编号为00,01,…,59,现从中抽取一个容量为7的样本,
从随机数表的倒数第5行第11~12列开始,向下读取,到最后一行后向右18,81(舍去),90(舍去),82(舍去),05,98(舍去),90(舍去),07,35,82(舍去),96(舍去),59,26,94(舍去),66(舍去),39共7个;
所以抽取样本的号码是18,05,07,35,59,26,39.
14.如图所示是一次考试结果的频率直方图,则据此估计这次考试的平均分为________分.
答案 75
解析 利用组中值估算平均分,则有=55×0.1+65×0.2+75×0.4+85×0.2+95×0.1=75,故估计这次考试的平均分为75分.
15.数据3.2,3.6,4.5,2.4,4.6,6.4,7.8,7.9,8.0,8.1,8.4,8.6的50百分位数是________,75百分位数是________.
答案 7.1 8.05
解析 把这组数据从小到大排列得2.4,3.2,3.6,4.5,4.6,6.4,7.8,7.9,8.0,8.1,8.4,8.6,
∵50×=6,75×=9,
∴这组数据的50百分位数是=7.1,
75百分位数是=8.05.
16.学校开展“书香校园”活动以来,受到同学们的广泛关注.学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计图表.
若该组数的平均数、众数、中位数依次为a,b,c,则a,b,c的大小关系为________.
答案 a解析 依题意有
次数 0次 1次 2次 3次 4次
人数 7人 13人 17人 10人 3人
共统计了50人,众数为2,中位数为2,
∴平均数为=<2,
∴a四、解答题(本大题共6小题,共70分)
17.(10分)为了对某课题进行讨论研究,用分层抽样的方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人).
高校 相关人数 抽取人数
A x 1
B 36 y
C 54 3
(1)求x,y;
(2)若从高校B相关人员中选2人作专题发言,应采用什么抽样法?请写出合理的抽样过程.
解 (1)分层抽样是按各层相关人数和抽取人数的比例进行的,所以由=得x=18,=得y=2.故x=18,y=2.
(2)总体容量和样本容量较小,所以应采用抽签法,过程如下:
第一步,将36人随机编号,号码为1,2,3,…,36;
第二步,将号码分别写在相同的纸片上,揉成团,制成号签;
第三步,将号签放入一个不透明的容器中,充分搅拌,依次不放回地抽取2个号码,并记录上面的编号;
第四步,把与号码相对应的人选出,即可得到所要的样本.
18.(12分)为了了解小学生的体能情况,抽取某校一个年级的部分学生进行一分钟跳绳次数的测试,将数据整理后,画出频率直方图(如图所示).已知图中从左到右前三个小组的频率分别为0.1,0.3,0.4,且第一小组的频数为5.
(1)求第四小组的频率;
(2)求参加这次测试的学生的人数;
(3)若一分钟跳绳次数在75次以上(含75次)为达标,试估计该年级学生跳绳测试的达标率.
解 (1)第四小组的频率为1-0.1-0.3-0.4=0.2.
(2)设参加这次测试的学生有x人,则0.1x=5,
∴x=50,故参加这次测试的学生有50人.
(3)由题意,样本的达标率约为0.3+0.4+0.2=0.9,
∴估计该年级学生跳绳测试的达标率为90%.
19.(12分)某公司共有员工120人,用简单随机抽样任意抽取12人,得到这12人的月工资(单位:千元)如下:
7.5,6.8,8.6,6.2,7.8,8.9,7.8,8.0,8.5,8.2,7.2,8.0,试估计该公司员工工资的25,50,90百分位数.
解 将所有数据从小到大排列,得6.2,6.8,7.2,7.5,7.8,7.8,8.0,8.0,8.2,8.5,8.6,8.9,
因为有12个数据,
所以25×=3,50×=6,90×=10.8.
所以25百分位数为=7.35,
50百分位数为=7.9,
90百分位数为8.6.
所以估计该公司员工工资的25,50,90百分位数分别为7.35,7.9,8.6.
20.(12分)甲、乙两位同学进行投篮比赛,每人玩5局,每局在指定线外投篮,若第一次不进,再投第二次,依此类推,但最多只能投6次.当投进时,该局结束,并记下投篮的次数.当6次投不进,该局也结束,记为“×”.第一次投进得6分,第二次投进得5分,第三次投进得4分,依此类推,第6次投不进,得0分.两人的投篮情况如下:
第1局 第2局 第3局 第4局 第5局
甲 5次 × 4次 5次 1次
乙 × 2次 4次 2次 ×
请通过计算,判断哪位同学投篮的水平高.
解 依题意,甲、乙的得分情况如下表:
第1局 第2局 第3局 第4局 第5局
甲 2 0 3 2 6
乙 0 5 3 5 0
甲=×(2+0+3+2+6)=2.6,
s甲=≈1.96,
乙=×(0+5+3+5+0)=2.6,
s乙=≈2.24,
因为甲得分的平均数与乙得分的平均数相等,
甲得分的标准差小于乙得分的标准差,甲投篮得分比乙稳定,故甲投篮的水平高.
21.(12分)为了了解某市参加2021年全国高中数学联赛的学生考试结果情况,从中选取60名同学将其成绩(百分制,均为正数)分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组后,得到部分频率直方图(如图),观察图形,回答下列问题:
(1)求分数在[70,80)内的频率,并补全这个频率直方图;
(2)根据频率直方图,估计本次考试成绩的众数、平均数;
(3)根据评奖规则,排名靠前10%的同学可以获奖,请你估计获奖的同学至少需要多少分?
解 (1)设分数在[70,80)内的频率为x,根据频率直方图,则有(0.01+0.015+0.02+0.025+0.005)×10+x=1,可得x=0.25,
∴分数在[70,80)内的频率为0.25.
补全频率直方图为:
(2)由图知,众数为75和85,
平均数为45×0.10+55×0.15+65×0.2+75×0.25+85×0.25+95×0.05=70.5.
(3)因为分数在[80,90)内的频率为0.25,[90,100]内的频率为0.05,
而0.05<10%<(0.25+0.05),
所以得分前10%的分界点应在80至90之间.
设所求的分界点为90-x,
则0.025x+0.005×10=10%,解得x=2.
所以得分前10%的分界点为88,即获奖的同学至少需要88分.
22.(12分)某初级中学共有学生2 000名,各年级男、女生人数如下表:
初一年级 初二年级 初三年级
女生 373 x y
男生 377 370 z
已知在全校学生中随机抽取1名,抽到初二年级女生的频率是0.19.
(1)求x的值;
(2)现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
(3)在(2)中,若所抽取的初一年级、初二年级、初三年级三个年级学生的体重的平均数分别是40 kg,50 kg,60 kg,方差分别是1,2,3,估计该校所有学生体重的平均数和方差.
解 (1)∵=0.19,∴x=380.
(2)初三年级人数为y+z=2 000-(373+377+380+370)=500,现用分层抽样的方法在全校抽取48名学生,应在初三年级抽取的人数为×500=12.
(3)初一年级应抽取学生的人数为×750=18,
初二年级应抽取学生的人数为×750=18,
∴该校所有学生体重的平均数约为=×40+×50+×60=48.75(kg),
该校所有学生体重的方差约为
s2=×[1+(40-48.75)2]+×[2+(50-48.75)2]+×[3+(60-48.75)2]=62.812 5.
(时间:120分钟 满分:150分)
一、单项选择题(本大题共8小题,每小题5分,共40分)
1.为了了解所加工的一批零件的长度,抽测了其中200个零件的长度,在这个问题中,200个零件的长度是( )
A.总体 B.个体
C.总体的一个样本 D.样本容量
2.①一次数学考试中,某班有10人的成绩在100分以上,32人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人了解有关情况;②运动会的工作人员为参加4×100 m接力赛的6支队伍安排跑道.针对这两件事,恰当的抽样方法分别为( )
A.分层抽样,简单随机抽样
B.简单随机抽样,简单随机抽样
C.简单随机抽样,分层抽样
D.分层抽样,分层抽样
3.为了调查学生每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.样本容量为1 000的频率直方图如图所示,则样本数据落在[6,14)内的频数为( )
A.780 B.680 C.648 D.460
4.某校高二年级有50人参加2021“希望杯”数学竞赛,他们竞赛的成绩制成了如下的频率分布表,根据该表估计该校学生数学竞赛成绩的平均分为( )
分组 [60,70) [70,80) [80,90) [90,100]
频率 0.2 0.4 0.3 0.1
A.70 B.73 C.78 D.81.5
5.我国古代数学专著《九章算术》中有一衰分问题:今有北乡八千一百人,西乡七千四百八十八人,南乡六千九百一十二人,凡三乡,发役三百人,则北乡遣( )
A.104人 B.108人 C.112人 D.120人
6.如图是某班50名学生期中考试数学成绩的频率直方图,其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],则图中x的值等于( )
A.0.120 B.0.180
C.0.012 D.0.018
7.为了在射击比赛中取得优异成绩,某国拟从甲、乙两位选手中派出一位随代表团参赛,现两人进行了5次射击,射击成绩如下表(单位:分),则应派出选手及其标准差为( )
次数 选手 第一次 第二次 第三次 第四次 第五次
甲 7.4 8.1 8.6 8.0 7.9
乙 7.8 8.4 7.6 8.1 8.1
A.甲,0.148 B.乙,0.076
C.甲,2 D.乙,2
8.某校为了对初三学生的体重进行摸底调查,随机抽取了50名学生的体重(kg),将所得数据整理后,画出了频率直方图,如图所示 ,体重在[45,50)内适合跑步训练,体重在[50,55)内适合跳远训练,体重在[55,60]内适合投掷相关方面训练,估计该校初三学生适合参加跑步、跳远、投掷三项训练的集训人数之比为( )
A.4∶3∶1 B.5∶3∶1
C.5∶3∶2 D.3∶2∶1
二、多项选择题(本大题共4小题,每小题5分,共20分.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.甲、乙两支女子曲棍球队在去年的国际冠军杯中,甲队平均每场进球数是3.2,全年进球数的标准差为3;乙队平均每场进球数是1.8,全年进球数的标准差为0.3.下列说法中,正确的是( )
A.甲队技术比乙队好
B.甲队发挥比乙队稳定
C.乙队几乎每场都进球
D.甲队的表现时好时坏
10.如图1为某省2021年1~4月份快递业务量统计图,图2为该省2021年1~4月份快递业务收入统计图,对统计图理解正确的是( )
图1
图2
A.2021年1~4月份快递业务量3月份最高,2月份最低,差值接近2 000万件
B.2021年1~4月份快递业务量同比增长率均超过50%,在3月份最高,和春节蛰伏后网购迎来喷涨有关
C.从两图中看,业务量与业务收入变化高度一致
D.从1~4月份来看,业务量与业务收入有波动,但整体保持高速增长
11.某学校为了调查学生在一周生活方面的支出情况,抽出了一个容量为n的样本,其频率直方图如图所示,其中支出在[50,60]元的学生有60人,则下列说法正确的是 ( )
A.样本中支出在[50,60]元的频率为0.03
B.样本中支出不少于40元的人数有132
C.n的值为200
D.若该校有2 000名学生,则一定有600人支出在[50,60]元
12.某赛季甲、乙两名篮球运动员各6场比赛得分情况记录如下,
甲:18,20,35,33,47,41;
乙:17,26,19,27,19,29.
则下列四个结论中,正确的是( )
A.甲运动员得分的极差大于乙运动员得分的极差
B.甲运动员得分的中位数大于乙运动员得分的中位数
C.甲运动员得分的平均数大于乙运动员得分的平均数
D.甲运动员的成绩比乙运动员的成绩稳定
三、填空题(本大题共4小题,每小题5分,共20分)
13.一个总体容量为60,其中的个体编号为00,01,02,…,59.现需从中抽取一个容量为7的样本,请从随机数表的倒数第5行(下表为随机数表的最后5行)第11~12列的18开始,依次向下,到最后一行后向右,直到取足样本,则抽取样本的号码是________.
95 33 95 22 00 18 74 72 00 18 46 40 62 98 80 54 97 20 56 95
38 79 58 69 32 81 76 80 26 92 15 74 80 08 32 16 46 70 50 80
82 80 84 25 39 90 84 60 79 80 67 72 16 42 79 71 59 73 05 50
24 36 59 87 38 82 07 53 89 35 08 22 23 71 77 91 01 93 20 49
96 35 23 79 18 05 98 90 07 35 82 96 59 26 94 66 39 67 98 60
14.如图所示是一次考试结果的频率直方图,则据此估计这次考试的平均分为________分.
15.数据3.2,3.6,4.5,2.4,4.6,6.4,7.8,7.9,8.0,8.1,8.4,8.6的50百分位数是________,75百分位数是________.
16.学校开展“书香校园”活动以来,受到同学们的广泛关注.学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计图表.
若该组数的平均数、众数、中位数依次为a,b,c,则a,b,c的大小关系为________.
四、解答题(本大题共6小题,共70分)
17.(10分)为了对某课题进行讨论研究,用分层抽样的方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人).
高校 相关人数 抽取人数
A x 1
B 36 y
C 54 3
(1)求x,y;
(2)若从高校B相关人员中选2人作专题发言,应采用什么抽样法?请写出合理的抽样过程.
18.(12分)为了了解小学生的体能情况,抽取某校一个年级的部分学生进行一分钟跳绳次数的测试,将数据整理后,画出频率直方图(如图所示).已知图中从左到右前三个小组的频率分别为0.1,0.3,0.4,且第一小组的频数为5.
(1)求第四小组的频率;
(2)求参加这次测试的学生的人数;
(3)若一分钟跳绳次数在75次以上(含75次)为达标,试估计该年级学生跳绳测试的达标率.
19.(12分)某公司共有员工120人,用简单随机抽样任意抽取12人,得到这12人的月工资(单位:千元)如下:
7.5,6.8,8.6,6.2,7.8,8.9,7.8,8.0,8.5,8.2,7.2,8.0,试估计该公司员工工资的25,50,90百分位数.
20.(12分)甲、乙两位同学进行投篮比赛,每人玩5局,每局在指定线外投篮,若第一次不进,再投第二次,依此类推,但最多只能投6次.当投进时,该局结束,并记下投篮的次数.当6次投不进,该局也结束,记为“×”.第一次投进得6分,第二次投进得5分,第三次投进得4分,依此类推,第6次投不进,得0分.两人的投篮情况如下:
第1局 第2局 第3局 第4局 第5局
甲 5次 × 4次 5次 1次
乙 × 2次 4次 2次 ×
请通过计算,判断哪位同学投篮的水平高.
21.(12分)为了了解某市参加2021年全国高中数学联赛的学生考试结果情况,从中选取60名同学将其成绩(百分制,均为正数)分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组后,得到部分频率直方图(如图),观察图形,回答下列问题:
(1)求分数在[70,80)内的频率,并补全这个频率直方图;
(2)根据频率直方图,估计本次考试成绩的众数、平均数;
(3)根据评奖规则,排名靠前10%的同学可以获奖,请你估计获奖的同学至少需要多少分?
22.(12分)某初级中学共有学生2 000名,各年级男、女生人数如下表:
初一年级 初二年级 初三年级
女生 373 x y
男生 377 370 z
已知在全校学生中随机抽取1名,抽到初二年级女生的频率是0.19.
(1)求x的值;
(2)现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
(3)在(2)中,若所抽取的初一年级、初二年级、初三年级三个年级学生的体重的平均数分别是40 kg,50 kg,60 kg,方差分别是1,2,3,估计该校所有学生体重的平均数和方差.
章末检测试卷六(第14章)
(时间:120分钟 满分:150分)
一、单项选择题(本大题共8小题,每小题5分,共40分)
1.为了了解所加工的一批零件的长度,抽测了其中200个零件的长度,在这个问题中,200个零件的长度是( )
A.总体 B.个体
C.总体的一个样本 D.样本容量
答案 C
解析 总体是这批零件的长度,个体是这批零件中每个零件的长度,样本是抽取的200个零件的长度,样本容量是200.
2.①一次数学考试中,某班有10人的成绩在100分以上,32人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人了解有关情况;②运动会的工作人员为参加4×100 m接力赛的6支队伍安排跑道.针对这两件事,恰当的抽样方法分别为( )
A.分层抽样,简单随机抽样
B.简单随机抽样,简单随机抽样
C.简单随机抽样,分层抽样
D.分层抽样,分层抽样
答案 A
解析 ①中,考试成绩在不同分数段之间的同学有明显的差异,用分层抽样比较恰当;②中,总体包含的个体较少,用简单随机抽样比较恰当.
3.为了调查学生每天零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.样本容量为1 000的频率直方图如图所示,则样本数据落在[6,14)内的频数为( )
A.780 B.680 C.648 D.460
答案 B
解析 频率直方图中每个小长方形的面积就是相应的频率,所以1 000-(0.02×4+0.03×4×2)×1 000=680.
4.某校高二年级有50人参加2021“希望杯”数学竞赛,他们竞赛的成绩制成了如下的频率分布表,根据该表估计该校学生数学竞赛成绩的平均分为( )
分组 [60,70) [70,80) [80,90) [90,100]
频率 0.2 0.4 0.3 0.1
A.70 B.73 C.78 D.81.5
答案 C
解析 估计该校学生数学竞赛成绩的平均分=65×0.2+75×0.4+85×0.3+95×0.1=78,故选C.
5.我国古代数学专著《九章算术》中有一衰分问题:今有北乡八千一百人,西乡七千四百八十八人,南乡六千九百一十二人,凡三乡,发役三百人,则北乡遣( )
A.104人 B.108人 C.112人 D.120人
答案 B
解析 由题意可知,这是一个分层抽样的问题,其中北乡可抽取的人数为300×=300×=108,故选B.
6.如图是某班50名学生期中考试数学成绩的频率直方图,其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],则图中x的值等于( )
A.0.120 B.0.180
C.0.012 D.0.018
答案 D
解析 由题图可知纵坐标表示.
故x=0.1-0.054-0.010-0.006-0.006-0.006=0.018.
7.为了在射击比赛中取得优异成绩,某国拟从甲、乙两位选手中派出一位随代表团参赛,现两人进行了5次射击,射击成绩如下表(单位:分),则应派出选手及其标准差为( )
次数 选手 第一次 第二次 第三次 第四次 第五次
甲 7.4 8.1 8.6 8.0 7.9
乙 7.8 8.4 7.6 8.1 8.1
A.甲,0.148 B.乙,0.076
C.甲,2 D.乙,2
答案 D
解析 甲选手成绩的平均数为=8.0,
方差为[(7.4-8)2+(8.1-8)2+(8.6-8)2+(8-8)2+(7.9-8)2]=0.148,
乙选手成绩的平均数为=8.0,
方差为[(7.8-8)2+(8.4-8)2+(7.6-8)2+(8.1-8)2+(8.1-8)2]=0.076,
甲、乙成绩的平均数相同,但乙方差较小,故乙的成绩较稳定,
应选乙,其标准差为=2,故选D.
8.某校为了对初三学生的体重进行摸底调查,随机抽取了50名学生的体重(kg),将所得数据整理后,画出了频率直方图,如图所示 ,体重在[45,50)内适合跑步训练,体重在[50,55)内适合跳远训练,体重在[55,60]内适合投掷相关方面训练,估计该校初三学生适合参加跑步、跳远、投掷三项训练的集训人数之比为( )
A.4∶3∶1 B.5∶3∶1
C.5∶3∶2 D.3∶2∶1
答案 B
解析 体重在[45,50)内的频率为0.1×5=0.5,体重在[50,55)内的频率为0.06×5=0.3,体重在[55,60]内的频率为0.02×5=0.1,
∵0.5∶0.3∶0.1=5∶3∶1,
∴可估计该校初三学生适合参加跑步、跳远、投掷三项训练的集训人数之比为5∶3∶1,故选B.
二、多项选择题(本大题共4小题,每小题5分,共20分.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.甲、乙两支女子曲棍球队在去年的国际冠军杯中,甲队平均每场进球数是3.2,全年进球数的标准差为3;乙队平均每场进球数是1.8,全年进球数的标准差为0.3.下列说法中,正确的是( )
A.甲队技术比乙队好
B.甲队发挥比乙队稳定
C.乙队几乎每场都进球
D.甲队的表现时好时坏
答案 ACD
解析 因为甲队的平均进球数比乙队多,所以甲队技术较好,A正确;乙队的标准差比甲队小,标准差越小越稳定,所以乙队发挥稳定,B错误;乙队平均每场进球数为1.8,且乙队全年进球数的标准差较小,所以乙队几乎每场都进球,C正确;由于s甲=3,s乙=0.3,所以甲队与乙队相比,不稳定,所以甲队的表现时好时坏,D正确.
10.如图1为某省2021年1~4月份快递业务量统计图,图2为该省2021年1~4月份快递业务收入统计图,对统计图理解正确的是( )
图1
图2
A.2021年1~4月份快递业务量3月份最高,2月份最低,差值接近2 000万件
B.2021年1~4月份快递业务量同比增长率均超过50%,在3月份最高,和春节蛰伏后网购迎来喷涨有关
C.从两图中看,业务量与业务收入变化高度一致
D.从1~4月份来看,业务量与业务收入有波动,但整体保持高速增长
答案 ABC
解析 由图1可知快递业务量3月份为4 397万件,2月份为2 411万件,差值为4 397-2 411=1 986(万件),故A正确;由图1可知B也正确;对于C,由两图易知业务量从高到低变化是3月→4月→1月→2月,业务收入从高到低变化是3月→4月→1月→2月,保持高度一致,所以C正确;对于D,由图知业务收入2月比1月减少,4月比3月减少,整体不具备高速增长之说,所以D不正确.
11.某学校为了调查学生在一周生活方面的支出情况,抽出了一个容量为n的样本,其频率直方图如图所示,其中支出在[50,60]元的学生有60人,则下列说法正确的是 ( )
A.样本中支出在[50,60]元的频率为0.03
B.样本中支出不少于40元的人数有132
C.n的值为200
D.若该校有2 000名学生,则一定有600人支出在[50,60]元
答案 BC
解析 由频率直方图得,
在A中,样本中支出在[50,60]元的频率为1-(0.01+0.024+0.036)×10=0.3,故A错误;
在B中,样本中支出不少于40元的人数有×0.36+60=132,故B正确;
在C中,n==200,故n的值为200,故C正确;
D.若该校有2 000名学生,则可能有600人支出在[50,60]元,故D错误.
12.某赛季甲、乙两名篮球运动员各6场比赛得分情况记录如下,
甲:18,20,35,33,47,41;
乙:17,26,19,27,19,29.
则下列四个结论中,正确的是( )
A.甲运动员得分的极差大于乙运动员得分的极差
B.甲运动员得分的中位数大于乙运动员得分的中位数
C.甲运动员得分的平均数大于乙运动员得分的平均数
D.甲运动员的成绩比乙运动员的成绩稳定
答案 ABC
解析 对于A,甲运动员得分的极差为47-18=29,乙运动员得分的极差为29-17=12,甲运动员得分的极差大于乙运动员得分的极差,因此A正确;
对于B,甲的数据从小到大排列后,处于中间的数是33,35,所以甲运动员得分的中位数是34,同理求得乙运动员得分的中位数是22.5,因此甲运动员得分的中位数大于乙运动员得分的中位数,故B正确;
对于C,甲运动员得分的平均数为≈32.33,乙运动员得分的平均数为≈22.83,因此甲运动员得分的平均数大于乙运动员得分的平均数,故C正确;
对于D,分别计算甲、乙两个运动员得分的方差,方差小的成绩更稳定.可以算出甲的方差为s≈109.22,乙的方差为s≈21.47,因为乙的方差小于甲的方差,所以乙运动员的成绩比甲运动员的成绩稳定,故D不正确.
三、填空题(本大题共4小题,每小题5分,共20分)
13.一个总体容量为60,其中的个体编号为00,01,02,…,59.现需从中抽取一个容量为7的样本,请从随机数表的倒数第5行(下表为随机数表的最后5行)第11~12列的18开始,依次向下,到最后一行后向右,直到取足样本,则抽取样本的号码是________.
95 33 95 22 00 18 74 72 00 18 46 40 62 98 80 54 97 20 56 95
38 79 58 69 32 81 76 80 26 92 15 74 80 08 32 16 46 70 50 80
82 80 84 25 39 90 84 60 79 80 67 72 16 42 79 71 59 73 05 50
24 36 59 87 38 82 07 53 89 35 08 22 23 71 77 91 01 93 20 49
96 35 23 79 18 05 98 90 07 35 82 96 59 26 94 66 39 67 98 60
答案 18,05,07,35,59,26,39.
解析 根据题意,60个个体编号为00,01,…,59,现从中抽取一个容量为7的样本,
从随机数表的倒数第5行第11~12列开始,向下读取,到最后一行后向右18,81(舍去),90(舍去),82(舍去),05,98(舍去),90(舍去),07,35,82(舍去),96(舍去),59,26,94(舍去),66(舍去),39共7个;
所以抽取样本的号码是18,05,07,35,59,26,39.
14.如图所示是一次考试结果的频率直方图,则据此估计这次考试的平均分为________分.
答案 75
解析 利用组中值估算平均分,则有=55×0.1+65×0.2+75×0.4+85×0.2+95×0.1=75,故估计这次考试的平均分为75分.
15.数据3.2,3.6,4.5,2.4,4.6,6.4,7.8,7.9,8.0,8.1,8.4,8.6的50百分位数是________,75百分位数是________.
答案 7.1 8.05
解析 把这组数据从小到大排列得2.4,3.2,3.6,4.5,4.6,6.4,7.8,7.9,8.0,8.1,8.4,8.6,
∵50×=6,75×=9,
∴这组数据的50百分位数是=7.1,
75百分位数是=8.05.
16.学校开展“书香校园”活动以来,受到同学们的广泛关注.学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计图表.
若该组数的平均数、众数、中位数依次为a,b,c,则a,b,c的大小关系为________.
答案 a
次数 0次 1次 2次 3次 4次
人数 7人 13人 17人 10人 3人
共统计了50人,众数为2,中位数为2,
∴平均数为=<2,
∴a
17.(10分)为了对某课题进行讨论研究,用分层抽样的方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人).
高校 相关人数 抽取人数
A x 1
B 36 y
C 54 3
(1)求x,y;
(2)若从高校B相关人员中选2人作专题发言,应采用什么抽样法?请写出合理的抽样过程.
解 (1)分层抽样是按各层相关人数和抽取人数的比例进行的,所以由=得x=18,=得y=2.故x=18,y=2.
(2)总体容量和样本容量较小,所以应采用抽签法,过程如下:
第一步,将36人随机编号,号码为1,2,3,…,36;
第二步,将号码分别写在相同的纸片上,揉成团,制成号签;
第三步,将号签放入一个不透明的容器中,充分搅拌,依次不放回地抽取2个号码,并记录上面的编号;
第四步,把与号码相对应的人选出,即可得到所要的样本.
18.(12分)为了了解小学生的体能情况,抽取某校一个年级的部分学生进行一分钟跳绳次数的测试,将数据整理后,画出频率直方图(如图所示).已知图中从左到右前三个小组的频率分别为0.1,0.3,0.4,且第一小组的频数为5.
(1)求第四小组的频率;
(2)求参加这次测试的学生的人数;
(3)若一分钟跳绳次数在75次以上(含75次)为达标,试估计该年级学生跳绳测试的达标率.
解 (1)第四小组的频率为1-0.1-0.3-0.4=0.2.
(2)设参加这次测试的学生有x人,则0.1x=5,
∴x=50,故参加这次测试的学生有50人.
(3)由题意,样本的达标率约为0.3+0.4+0.2=0.9,
∴估计该年级学生跳绳测试的达标率为90%.
19.(12分)某公司共有员工120人,用简单随机抽样任意抽取12人,得到这12人的月工资(单位:千元)如下:
7.5,6.8,8.6,6.2,7.8,8.9,7.8,8.0,8.5,8.2,7.2,8.0,试估计该公司员工工资的25,50,90百分位数.
解 将所有数据从小到大排列,得6.2,6.8,7.2,7.5,7.8,7.8,8.0,8.0,8.2,8.5,8.6,8.9,
因为有12个数据,
所以25×=3,50×=6,90×=10.8.
所以25百分位数为=7.35,
50百分位数为=7.9,
90百分位数为8.6.
所以估计该公司员工工资的25,50,90百分位数分别为7.35,7.9,8.6.
20.(12分)甲、乙两位同学进行投篮比赛,每人玩5局,每局在指定线外投篮,若第一次不进,再投第二次,依此类推,但最多只能投6次.当投进时,该局结束,并记下投篮的次数.当6次投不进,该局也结束,记为“×”.第一次投进得6分,第二次投进得5分,第三次投进得4分,依此类推,第6次投不进,得0分.两人的投篮情况如下:
第1局 第2局 第3局 第4局 第5局
甲 5次 × 4次 5次 1次
乙 × 2次 4次 2次 ×
请通过计算,判断哪位同学投篮的水平高.
解 依题意,甲、乙的得分情况如下表:
第1局 第2局 第3局 第4局 第5局
甲 2 0 3 2 6
乙 0 5 3 5 0
甲=×(2+0+3+2+6)=2.6,
s甲=≈1.96,
乙=×(0+5+3+5+0)=2.6,
s乙=≈2.24,
因为甲得分的平均数与乙得分的平均数相等,
甲得分的标准差小于乙得分的标准差,甲投篮得分比乙稳定,故甲投篮的水平高.
21.(12分)为了了解某市参加2021年全国高中数学联赛的学生考试结果情况,从中选取60名同学将其成绩(百分制,均为正数)分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组后,得到部分频率直方图(如图),观察图形,回答下列问题:
(1)求分数在[70,80)内的频率,并补全这个频率直方图;
(2)根据频率直方图,估计本次考试成绩的众数、平均数;
(3)根据评奖规则,排名靠前10%的同学可以获奖,请你估计获奖的同学至少需要多少分?
解 (1)设分数在[70,80)内的频率为x,根据频率直方图,则有(0.01+0.015+0.02+0.025+0.005)×10+x=1,可得x=0.25,
∴分数在[70,80)内的频率为0.25.
补全频率直方图为:
(2)由图知,众数为75和85,
平均数为45×0.10+55×0.15+65×0.2+75×0.25+85×0.25+95×0.05=70.5.
(3)因为分数在[80,90)内的频率为0.25,[90,100]内的频率为0.05,
而0.05<10%<(0.25+0.05),
所以得分前10%的分界点应在80至90之间.
设所求的分界点为90-x,
则0.025x+0.005×10=10%,解得x=2.
所以得分前10%的分界点为88,即获奖的同学至少需要88分.
22.(12分)某初级中学共有学生2 000名,各年级男、女生人数如下表:
初一年级 初二年级 初三年级
女生 373 x y
男生 377 370 z
已知在全校学生中随机抽取1名,抽到初二年级女生的频率是0.19.
(1)求x的值;
(2)现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
(3)在(2)中,若所抽取的初一年级、初二年级、初三年级三个年级学生的体重的平均数分别是40 kg,50 kg,60 kg,方差分别是1,2,3,估计该校所有学生体重的平均数和方差.
解 (1)∵=0.19,∴x=380.
(2)初三年级人数为y+z=2 000-(373+377+380+370)=500,现用分层抽样的方法在全校抽取48名学生,应在初三年级抽取的人数为×500=12.
(3)初一年级应抽取学生的人数为×750=18,
初二年级应抽取学生的人数为×750=18,
∴该校所有学生体重的平均数约为=×40+×50+×60=48.75(kg),
该校所有学生体重的方差约为
s2=×[1+(40-48.75)2]+×[2+(50-48.75)2]+×[3+(60-48.75)2]=62.812 5.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
