青岛版八年级上册数学 5.6《几何证明举例》(第1课时)课件(18张PPT)
文档属性
| 名称 | 青岛版八年级上册数学 5.6《几何证明举例》(第1课时)课件(18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 297.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-20 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
5.6几何证明举例
(第1课时)
在已学过的几何命题中,以下命题作为基本事实
1.两点确定一条直线.
2.两点之间线段最短
3.过一点有且只有一条直线与这条直线垂直;
4.两条直线被第三条直线所截,如果同位角相等,那么 两直线平行.
5.经过直线外一点有且只有一条直线与已知直线平行
6.两边及其夹角分别相等的两个三角形全等;
7.两角及其夹边分别相等的两个三角形全等;
8.三边分别相等的两个三角形全等;
SAS
ASA
SSS
1.在全等三角形的判定方法中是基本事实的有
第一关:基础知识关
2.你能证明不是基本事实的判定方法AAS 的
正确性吗?
(1)SAS、(2)ASA、(4)SSS
两角分别相等且其中一组等角的对边也相等的两个三角形全等
(1)根据题意,画出图形;
几何证明的过程一般包括三个步骤:
(2)结合图形,根据条件、结论,写出已知、求证
(3)找出由已知推出求证的途径,写出证明。
推理的依据只能是命题给出的已知条件、已经学过的定义、基本事实和已经证明过得定理
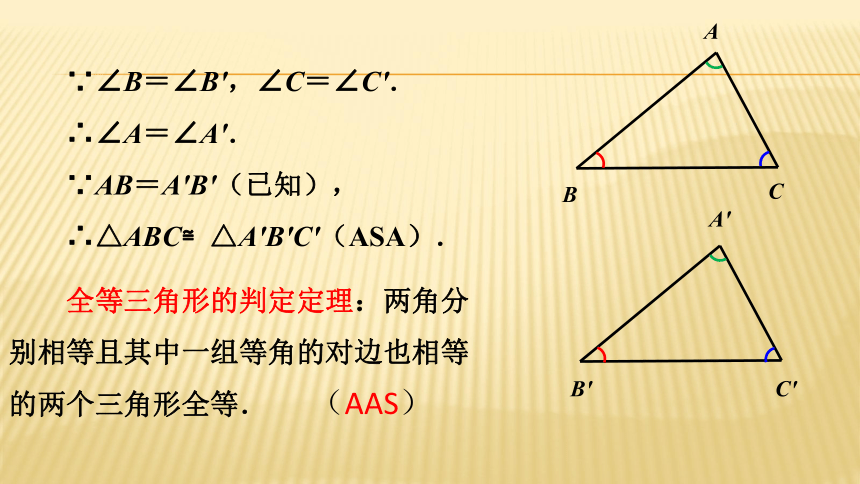
证明:在△ABC和△A'B'C'中,
∵∠A+∠B+∠C=180°,
∠A'+∠B'+∠C'=180°.
∴∠A=180°―∠B―∠C,∠A'=180°―∠B'―∠C'.
1.求证:两角分别相等且其中一组等 角的对边也相等的两个三角形全等.
第二关:知识应用关
已知:如图,在△ABC和△A'B'C'中,AB=A'B',∠B=∠B',∠C=∠C'
求证:△ABC≌△A'B'C'.
∵∠B=∠B',∠C=∠C'.
∴∠A=∠A'.
∵AB=A'B'(已知),
∴△ABC≌△A'B'C'(ASA).
A
B
C
A'
B'
C'
全等三角形的判定定理:两角分别相等且其中一组等角的对边也相等的两个三角形全等.
(AAS)
(1)判定两个三角形全等的方法?
(2)证明两个三角形全等的作用是什么?
用来证明线段相等或者角相等.
思考:
基本事实:SSS,SAS,ASA;
判定定理:AAS.
例1.已知:如图所示,AB=CB,AD=CD.
求证:∠A=∠C.
证明:连接DB.
∵AB=CD,AD=CD(已知),BD=BD(公共边),
∴△ABD≌△CBD(SSS),
∴∠A=∠C(全等三角形对应角的定义).
D
C
B
A
知识应用关
在△ABD和△CBD中,
证明两个角相等的方法:
(1)如果两个角在两个三角形中:证这两个角所在的三角形全等.
(2)如果这两个角不在两个三角形中,可通过添加辅助线的方法,构造两个全等三角形.
类比证明角相等的方法,如何证明两条线段相等呢?让我们进行“挑战自我”
作出两个全等三角形,你发现它们对应角的平分线有什么性质?对应边上的中线、对应边上的高有什么性质?证明你的结论.
第三关:知识拓展关
证明:∵△ABC≌△A'B'C'(已知),
∴AB=A'B'(全等三角形的对应边相等),
∠B=∠B',∠BAC=∠B'A'C'(全等三角形的对应角相等),
∵AD、A'D'分别平分∠BAC,∠B'A'C'(已知),
(1)求证:全等三角形的对应角的平分线相等.
已知:△ABC≌△A'B'C', AD、A'D'分别平分∠BAC,∠B'A'C',
求证:AD=A'D'.
知识拓展关
C
B
D
A
∴ AD=A'D' (全等三角形的对应边相等).
(1)求证:全等三角形的对应角的平分线相等.
已知:△ABC≌△A'B'C', AD、A'D'分别平分∠BAC,∠B'A'C',
求证:AD=A'D'.
知识拓展关
C
B
D
A
∴∠BAD= ∠BAC,
∠B'A'D'= ∠BAC(角平分线的定义),
∴∠BAD=∠B'A'D'(等量代换).
∴△ABD≌△A'B'D'(ASA).
求证:(2)全等三角形的对应边上的中线相等
已知:△ABC≌△A'B'C',AD、A'D'分别是△ABC和△A'B'C'的中线.
求证:AD=A'D'
知识拓展关
C
B
D
A
(3)求证:全等三角形的对应边上的高相等
已知:△ABC≌△A'B'C',AD、A'D'分别是△ABC和△A'B'C'的高.
求证:AD=A'D'.
知识拓展关
A
B
D
C
思考:怎样添加辅助线才能使∠A与∠C存在于两个全等三角形中而且是两个三角形的对应角呢?
第四关:自我检测关
已知:如图,AB=CD,AD=BC ,
求证: ∠A= ∠C
已知:如图AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,
求证: DE=DF
第五关:链接中考关
第六关:课堂总结关
这节课,你学会什么?有什么收获?说说看!
1.全等三角形的判定方法:
SAS
ASA
AAS
SSS
2.在证明两个角相等或两条线段相等时,可考察它们是否在给出的两个全等三角形中。如果不在,可以尝试添加辅助线,构造两个全等三角形。
作业:
教材P187习题5.6 1、 2、 3 、4
5.6几何证明举例
(第1课时)
在已学过的几何命题中,以下命题作为基本事实
1.两点确定一条直线.
2.两点之间线段最短
3.过一点有且只有一条直线与这条直线垂直;
4.两条直线被第三条直线所截,如果同位角相等,那么 两直线平行.
5.经过直线外一点有且只有一条直线与已知直线平行
6.两边及其夹角分别相等的两个三角形全等;
7.两角及其夹边分别相等的两个三角形全等;
8.三边分别相等的两个三角形全等;
SAS
ASA
SSS
1.在全等三角形的判定方法中是基本事实的有
第一关:基础知识关
2.你能证明不是基本事实的判定方法AAS 的
正确性吗?
(1)SAS、(2)ASA、(4)SSS
两角分别相等且其中一组等角的对边也相等的两个三角形全等
(1)根据题意,画出图形;
几何证明的过程一般包括三个步骤:
(2)结合图形,根据条件、结论,写出已知、求证
(3)找出由已知推出求证的途径,写出证明。
推理的依据只能是命题给出的已知条件、已经学过的定义、基本事实和已经证明过得定理
证明:在△ABC和△A'B'C'中,
∵∠A+∠B+∠C=180°,
∠A'+∠B'+∠C'=180°.
∴∠A=180°―∠B―∠C,∠A'=180°―∠B'―∠C'.
1.求证:两角分别相等且其中一组等 角的对边也相等的两个三角形全等.
第二关:知识应用关
已知:如图,在△ABC和△A'B'C'中,AB=A'B',∠B=∠B',∠C=∠C'
求证:△ABC≌△A'B'C'.
∵∠B=∠B',∠C=∠C'.
∴∠A=∠A'.
∵AB=A'B'(已知),
∴△ABC≌△A'B'C'(ASA).
A
B
C
A'
B'
C'
全等三角形的判定定理:两角分别相等且其中一组等角的对边也相等的两个三角形全等.
(AAS)
(1)判定两个三角形全等的方法?
(2)证明两个三角形全等的作用是什么?
用来证明线段相等或者角相等.
思考:
基本事实:SSS,SAS,ASA;
判定定理:AAS.
例1.已知:如图所示,AB=CB,AD=CD.
求证:∠A=∠C.
证明:连接DB.
∵AB=CD,AD=CD(已知),BD=BD(公共边),
∴△ABD≌△CBD(SSS),
∴∠A=∠C(全等三角形对应角的定义).
D
C
B
A
知识应用关
在△ABD和△CBD中,
证明两个角相等的方法:
(1)如果两个角在两个三角形中:证这两个角所在的三角形全等.
(2)如果这两个角不在两个三角形中,可通过添加辅助线的方法,构造两个全等三角形.
类比证明角相等的方法,如何证明两条线段相等呢?让我们进行“挑战自我”
作出两个全等三角形,你发现它们对应角的平分线有什么性质?对应边上的中线、对应边上的高有什么性质?证明你的结论.
第三关:知识拓展关
证明:∵△ABC≌△A'B'C'(已知),
∴AB=A'B'(全等三角形的对应边相等),
∠B=∠B',∠BAC=∠B'A'C'(全等三角形的对应角相等),
∵AD、A'D'分别平分∠BAC,∠B'A'C'(已知),
(1)求证:全等三角形的对应角的平分线相等.
已知:△ABC≌△A'B'C', AD、A'D'分别平分∠BAC,∠B'A'C',
求证:AD=A'D'.
知识拓展关
C
B
D
A
∴ AD=A'D' (全等三角形的对应边相等).
(1)求证:全等三角形的对应角的平分线相等.
已知:△ABC≌△A'B'C', AD、A'D'分别平分∠BAC,∠B'A'C',
求证:AD=A'D'.
知识拓展关
C
B
D
A
∴∠BAD= ∠BAC,
∠B'A'D'= ∠BAC(角平分线的定义),
∴∠BAD=∠B'A'D'(等量代换).
∴△ABD≌△A'B'D'(ASA).
求证:(2)全等三角形的对应边上的中线相等
已知:△ABC≌△A'B'C',AD、A'D'分别是△ABC和△A'B'C'的中线.
求证:AD=A'D'
知识拓展关
C
B
D
A
(3)求证:全等三角形的对应边上的高相等
已知:△ABC≌△A'B'C',AD、A'D'分别是△ABC和△A'B'C'的高.
求证:AD=A'D'.
知识拓展关
A
B
D
C
思考:怎样添加辅助线才能使∠A与∠C存在于两个全等三角形中而且是两个三角形的对应角呢?
第四关:自我检测关
已知:如图,AB=CD,AD=BC ,
求证: ∠A= ∠C
已知:如图AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,
求证: DE=DF
第五关:链接中考关
第六关:课堂总结关
这节课,你学会什么?有什么收获?说说看!
1.全等三角形的判定方法:
SAS
ASA
AAS
SSS
2.在证明两个角相等或两条线段相等时,可考察它们是否在给出的两个全等三角形中。如果不在,可以尝试添加辅助线,构造两个全等三角形。
作业:
教材P187习题5.6 1、 2、 3 、4
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
