人教新课标数学七年级下6.1平方根
文档属性
| 名称 | 人教新课标数学七年级下6.1平方根 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-08-03 00:00:00 | ||
图片预览










文档简介
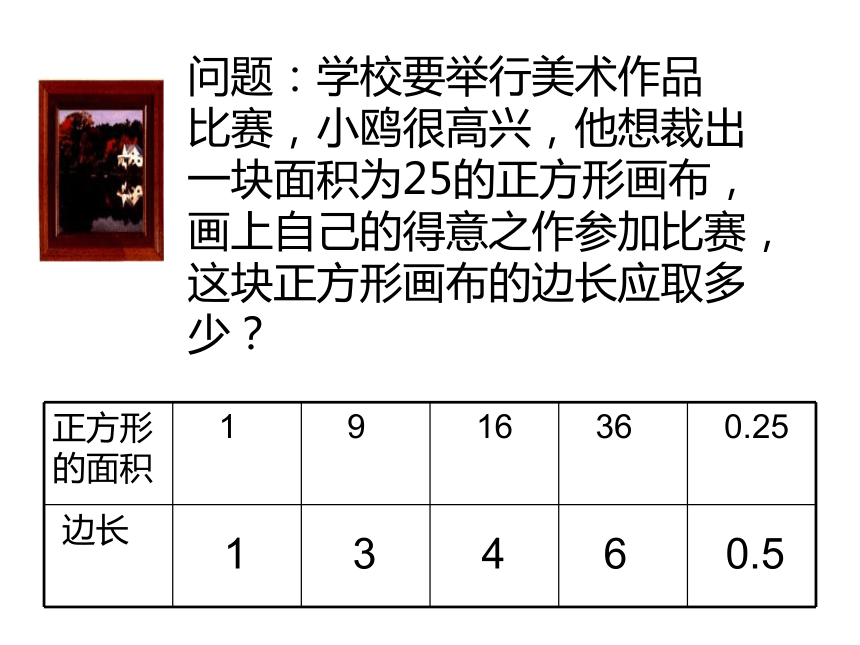
课件68张PPT。人教新课标 七年级下数学课件人教版七年级(下册)第六章实数6.1平方根(第一课时)问题:学校要举行美术作品
比赛,小鸥很高兴,他想裁出
一块面积为25的正方形画布,
画上自己的得意之作参加比赛,
这块正方形画布的边长应取多
少? 13460.5在括号里填上适当的正数.提示: 已知一个正数的平方,求这个正数的问题。120.8107 一般地,一个正数x的平方等于a,即 , 那么,这个正数x就叫做a的算术平方根.
记作: 读作:“根号a”
其中,a 叫做被开方数;
**规定:0的算术平方根为0 是一种运算符号 ,表示求一个数的算术平方根;算术平方根的概念:判断:
(1)5是25的算术平方根;
(2)-6是 36 的算术平方根;
(3)0的算术平方根是0;
(4)0.01是0.1的算术平方根;
(5)-5是-25的算术平方根。讨论:
1、负数有算术平方根吗?
2、 是什么数?
3, 中的a可以取任何数吗? *被开方数a是非负数,即 * 是非负数, 即负数没有平方根,因为没有一个正数的平方等于负数,
如: 无意义 记得做笔记哦!**也就是说,非负数的“算术”平方根是非负数。
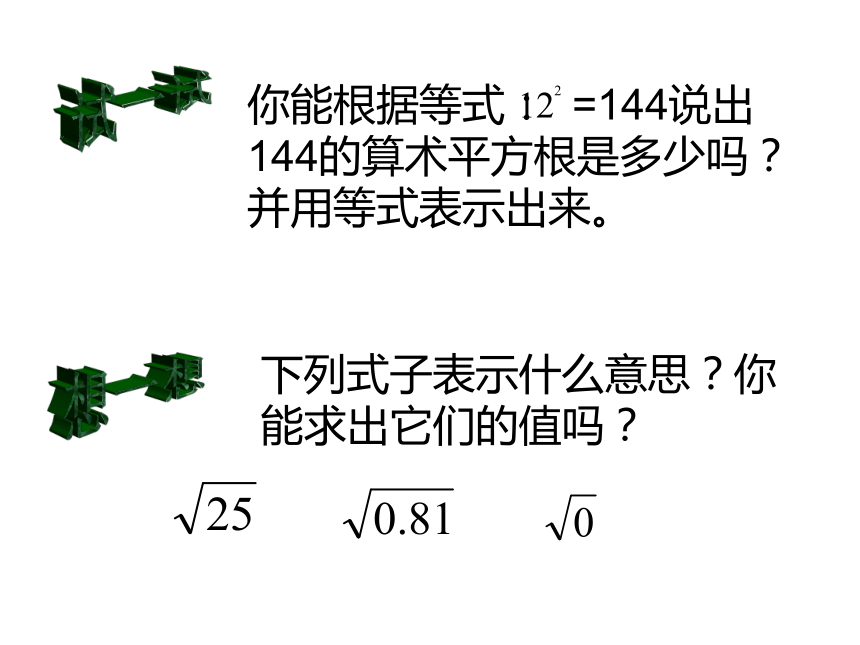
负数不存在算术平方根,即当 时, 无意义下列式子表示什么意思?试一试:你能根据等式122=144,说出144的算术平方根是多少吗?并用等式表示出来。练习:下列各式中哪些有意义?哪些无意义?为什么? 答:有意义的是无意义的是探究
1、a可以取任何数吗?
2、 是什么数?(1)被开方数a是非负数,即(2) 是非负数,即 也就是说,非负数的“算术”平方根是非负数。负数不存在算术平方根,即当 时, 无意义。如: 无意义 ; 8是64的算术平方根或 。(3) 是算术平方根的运算符号例1 求下列各数的算术平方根:
(1)100 (2) (3)0.0001解:(1)因为 =100,所以100的算术平方根为10,
即 =10。(2)因为 = ,所以 的算术平方根是
,即 =
(3)因为 =0.0001,所以0.0001的算术平方
根为0.01,即 =0.01。思考:1.下列各式哪些有意义,哪些没
有意义?
(1)- (2)
(3) (4)练习: 一、填空题:
(1)121的算术平方根是 ;
0.25的算术平方根是 ;
的算术平方根是 ;
0 的算术平方根是 ;
10-4的算术平方根是 ;
(2)100的算术平方根是 ; 的算术平方根是 ;
的算术平方根是 ;0.81的算术平方根是 ;110(3) 的算术平方根是 ;
0.0081 的算术平方根是 ;
2a 算术平方根是 ; 二、说下列各式所表示的意义,并分别求出它们的值。 :表示100的算术平方根,等于 ;:表示 的算术平方根,等于 ;0.09……请谈谈你的收获课本P69练习第1题、第2题.
今 日 作 业人教版七年级(下册)第六章实数6.1平方根(第二课时)复习1、 的算术平方根是( )
A 4 B ±16
C 16 D ±42、 的算术平方根是( )
A B
C D 复习3、面积为9的正方形的边长是 。5、如果 ,那么x = 。4、如果 ,那么x = 。探究 怎样将一个面积为1的小正方形拼
成一个面积为2的大正方形?面积为1边长为1面积为1面积为2边长为1边长为多少?设大正方形的边长为x,则
x2=2
由算术平方根的定义可知
x =
∴大正方形的边长是问题面积为2边长为思考: 究竟有多大?探究 的大小,可用估算的方法。探究用估算法探究 的大小∵ ,∴∴∵ ,∴∵ ,∴归纳无限不循环小数有限小数无限不循环小数无限不循环小数有限小数巩固 你能举出一些无限不循环小数
的例子吗? 下列各数是无限不循环小数吗?有限小数探究1、观察下列各式:小数点移位法则:被开方数小数点每向
右移动两位,结果小数点就向相同的方
向移动一位。探究2、观察下列各式:小数点移位法则:被开方数小数点每向
左移动两位,结果小数点就向相同的方
向移动一位。归纳小数点移位法则:被开方数小数点每向
左(右)移动两位,结果小数点就向相同
的方向移动一位。左移
两位左移
一位右移
两位右移
一位范例例1、已知 ,求:
(1) (2)
(3)根据小数点移位法则 巩固5、已知 , ,
求 、 的值。探究你能比较下列两个数的大小吗?与与化根号法估算法巩固6、估算大小:(1) 与(2) 与 小丽想用一块面积为 400cm2
正方形纸片,沿着边的方向裁出一块
面积为300cm2的长方形纸片用来绘
画,使它的长宽之比为3:2, 不知能否裁出来,正在发愁。小明见了说“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片”,你同意小明的说法吗? 小丽能用这块纸片裁出符合要求的纸片吗?例:小丽想用一块面积为400cm2的正方形纸片沿着边的方向裁出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2,不知能否裁出来,正在发愁,小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片”,你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?解:设长方形纸片的长为3x cm,宽为2x cm. 根据边长与面积的关系,得已知正方形纸片的边长只有20cm,这样,长方形纸片的长将大于正方形纸片的边长.答:不能同意小明的说法.小丽不能用这块正方形纸片裁出符合要求的长方形纸片.巩固7、一个正方形的展厅,它的面积为64
平方米,求它的周长。……请谈谈你的收获小结1、本节课你学了什么知识?2、你有什么体会?小数点移位法则数的大小比较方法 化根号法与估算法 利用算术平方根解决实际问题请同学们完成后面的作业。 今 日 作 业作业1、比较大小: (1) 与 (2) 与作业2、已知 , ,
求 、 、 、
的值。作业3、物体在自由落体运动中, ( g
是重力加速度,它的值约为10米/秒),
若物体降落高度h=125米,那么它降落
的时间是多少?人教版七年级(下册)第六章实数6.1平方根(第三课时)若x2=a(x≥0),那么x叫做a的算术平方根。
记作:x=一般地,如果一个数的平方等于a,
那么这个数叫做a的平方根或二次方根。即:若x2=a,那么x叫做a的平方根。
记作:x=求一个数a的平方根的运算,叫做开平方。149+1-1+2-2+3-3149+1-1+2-2+3-3开平方平方例如:∵∴5 和 -5 都是25的平方根。∵∴ 和 - 都是 的平方根。∴ 25的平方根是±5。±63±2试一试:(1)144的平方根是什么? (2)0的平方根是什么? (3) 的平方根是什么?
(4)-4的平方根是什么?为什么?从上面的回答中,你发现了什么?练习:下列说法中不正确的个数有 ( )
①0.25的平方根是0.5
②-0.5的平方 根是-0.25
③只有正数才有平方根
④0的平方根是0CA. 1个 B. 2个. C. 3个 D. 4个正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。a的一个平方根是3,则另一个平方根是 ,a= 。-393a-22和2a-3是m的两个平方根,
试求m的值。正数a的正的平方根叫做a的算术平方根。正数a的算术平方根记作:它的另一个平方根记作:一个正数a的平方根表示为:0的算术平方根还是0说明:这样求一个正数的平方根,只要求出它的算术平方根后,就可以写出它的平方根了。想一想 “负数没有平方根”与“一个数的平方根不能为负数”意义是否一样? 求一个数的平方根(二次方根)的运算,叫做开平方,开平方运算的结果就是平方根。平方与开平方是互为逆运算.举一个实际例子吧!5 的平方根,可以记作 和- ,或± 注意:因为负数没有平方根,所以在式子
中的被开方数 a ≥0 ,否则式子 没有意义。即式子 中的 a 是一个非负数。 例1:判断下列各数有没有平方根,如果有平方根,试求出它的平方根;如果没有平方根,说明理由。(1)81;
(2)-81;
(3)0;
(4) ;
(5) 。 例2:求下列各数的平方根。(1)100;(2)1.44;(3) ;(4)解: (1)∴100的平方根是±10即注意:不能写成请你妨照上面的例子完成其余三个小题。……请谈谈你的收获学习小结:本节课我们学习了哪些内容,你能回答吗?1.平方根的概念:一个数的平方等于a,这个数叫做a的平方根.2.平方根的性质:一个正数的平方根有两个,它们互为相反数.0的平方根还是0.负数没有平方根.3.平方根的表示法:4.算术平方根的概念:正数a的正的平方根叫做a的算术平方根比一比看谁最聪明?如图,求左圈和右圈中的表示的数:?练一练:
求出下列各数的平方根(1)225(2)(3)6.25(4)用计算器求下列各数的算术平方根(1) 529; (2)1225; (3)44.81思考: 你能求出下列各式中的未知数x吗?
(1) x2=49
(2)(x-1)2=25想一想判断下列说法是否正确.1. 的平方根是±16. ( ) 2. 一定是正数. ( )3.a2的算术平方根是a. ( )4.若 ,则a=-5. ( )5. . ( )6.-6是(-6)2的平方根. ( )7.若x2=36,则x= ( ) 8.如果两个数平方后相等,那么它们的也相等×××××√√例2. 已知 有意义,则x一定是 ( )
A.正数 B. 负数 C. 非负数 D. 非正数例3.求下列各式的值例3. 求使 有意义x的取值范围.例4.已知a、b满足等式 +︱b+5︱=0, 求a2-12b的算术平方根.X≤0补充练习;213256≥0-5互为相反数我们已学习了3种非负数,即绝对值、偶数次方、算术平方根。几个非负数的和为零,它们就同时为零,然后转化为方程(或方程组)来解。补充练习:练习:国际比赛的足球场的长在100m到110m之间,宽在64m到75m之间,现有一个长方形的足球场其长是宽的1.5倍,面积为7560m2,问:这个足球场能用作国际比赛吗?课本P76习题13.1第9题、第10题.
今 日 作 业
比赛,小鸥很高兴,他想裁出
一块面积为25的正方形画布,
画上自己的得意之作参加比赛,
这块正方形画布的边长应取多
少? 13460.5在括号里填上适当的正数.提示: 已知一个正数的平方,求这个正数的问题。120.8107 一般地,一个正数x的平方等于a,即 , 那么,这个正数x就叫做a的算术平方根.
记作: 读作:“根号a”
其中,a 叫做被开方数;
**规定:0的算术平方根为0 是一种运算符号 ,表示求一个数的算术平方根;算术平方根的概念:判断:
(1)5是25的算术平方根;
(2)-6是 36 的算术平方根;
(3)0的算术平方根是0;
(4)0.01是0.1的算术平方根;
(5)-5是-25的算术平方根。讨论:
1、负数有算术平方根吗?
2、 是什么数?
3, 中的a可以取任何数吗? *被开方数a是非负数,即 * 是非负数, 即负数没有平方根,因为没有一个正数的平方等于负数,
如: 无意义 记得做笔记哦!**也就是说,非负数的“算术”平方根是非负数。
负数不存在算术平方根,即当 时, 无意义下列式子表示什么意思?试一试:你能根据等式122=144,说出144的算术平方根是多少吗?并用等式表示出来。练习:下列各式中哪些有意义?哪些无意义?为什么? 答:有意义的是无意义的是探究
1、a可以取任何数吗?
2、 是什么数?(1)被开方数a是非负数,即(2) 是非负数,即 也就是说,非负数的“算术”平方根是非负数。负数不存在算术平方根,即当 时, 无意义。如: 无意义 ; 8是64的算术平方根或 。(3) 是算术平方根的运算符号例1 求下列各数的算术平方根:
(1)100 (2) (3)0.0001解:(1)因为 =100,所以100的算术平方根为10,
即 =10。(2)因为 = ,所以 的算术平方根是
,即 =
(3)因为 =0.0001,所以0.0001的算术平方
根为0.01,即 =0.01。思考:1.下列各式哪些有意义,哪些没
有意义?
(1)- (2)
(3) (4)练习: 一、填空题:
(1)121的算术平方根是 ;
0.25的算术平方根是 ;
的算术平方根是 ;
0 的算术平方根是 ;
10-4的算术平方根是 ;
(2)100的算术平方根是 ; 的算术平方根是 ;
的算术平方根是 ;0.81的算术平方根是 ;110(3) 的算术平方根是 ;
0.0081 的算术平方根是 ;
2a 算术平方根是 ; 二、说下列各式所表示的意义,并分别求出它们的值。 :表示100的算术平方根,等于 ;:表示 的算术平方根,等于 ;0.09……请谈谈你的收获课本P69练习第1题、第2题.
今 日 作 业人教版七年级(下册)第六章实数6.1平方根(第二课时)复习1、 的算术平方根是( )
A 4 B ±16
C 16 D ±42、 的算术平方根是( )
A B
C D 复习3、面积为9的正方形的边长是 。5、如果 ,那么x = 。4、如果 ,那么x = 。探究 怎样将一个面积为1的小正方形拼
成一个面积为2的大正方形?面积为1边长为1面积为1面积为2边长为1边长为多少?设大正方形的边长为x,则
x2=2
由算术平方根的定义可知
x =
∴大正方形的边长是问题面积为2边长为思考: 究竟有多大?探究 的大小,可用估算的方法。探究用估算法探究 的大小∵ ,∴∴∵ ,∴∵ ,∴归纳无限不循环小数有限小数无限不循环小数无限不循环小数有限小数巩固 你能举出一些无限不循环小数
的例子吗? 下列各数是无限不循环小数吗?有限小数探究1、观察下列各式:小数点移位法则:被开方数小数点每向
右移动两位,结果小数点就向相同的方
向移动一位。探究2、观察下列各式:小数点移位法则:被开方数小数点每向
左移动两位,结果小数点就向相同的方
向移动一位。归纳小数点移位法则:被开方数小数点每向
左(右)移动两位,结果小数点就向相同
的方向移动一位。左移
两位左移
一位右移
两位右移
一位范例例1、已知 ,求:
(1) (2)
(3)根据小数点移位法则 巩固5、已知 , ,
求 、 的值。探究你能比较下列两个数的大小吗?与与化根号法估算法巩固6、估算大小:(1) 与(2) 与 小丽想用一块面积为 400cm2
正方形纸片,沿着边的方向裁出一块
面积为300cm2的长方形纸片用来绘
画,使它的长宽之比为3:2, 不知能否裁出来,正在发愁。小明见了说“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片”,你同意小明的说法吗? 小丽能用这块纸片裁出符合要求的纸片吗?例:小丽想用一块面积为400cm2的正方形纸片沿着边的方向裁出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2,不知能否裁出来,正在发愁,小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片”,你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?解:设长方形纸片的长为3x cm,宽为2x cm. 根据边长与面积的关系,得已知正方形纸片的边长只有20cm,这样,长方形纸片的长将大于正方形纸片的边长.答:不能同意小明的说法.小丽不能用这块正方形纸片裁出符合要求的长方形纸片.巩固7、一个正方形的展厅,它的面积为64
平方米,求它的周长。……请谈谈你的收获小结1、本节课你学了什么知识?2、你有什么体会?小数点移位法则数的大小比较方法 化根号法与估算法 利用算术平方根解决实际问题请同学们完成后面的作业。 今 日 作 业作业1、比较大小: (1) 与 (2) 与作业2、已知 , ,
求 、 、 、
的值。作业3、物体在自由落体运动中, ( g
是重力加速度,它的值约为10米/秒),
若物体降落高度h=125米,那么它降落
的时间是多少?人教版七年级(下册)第六章实数6.1平方根(第三课时)若x2=a(x≥0),那么x叫做a的算术平方根。
记作:x=一般地,如果一个数的平方等于a,
那么这个数叫做a的平方根或二次方根。即:若x2=a,那么x叫做a的平方根。
记作:x=求一个数a的平方根的运算,叫做开平方。149+1-1+2-2+3-3149+1-1+2-2+3-3开平方平方例如:∵∴5 和 -5 都是25的平方根。∵∴ 和 - 都是 的平方根。∴ 25的平方根是±5。±63±2试一试:(1)144的平方根是什么? (2)0的平方根是什么? (3) 的平方根是什么?
(4)-4的平方根是什么?为什么?从上面的回答中,你发现了什么?练习:下列说法中不正确的个数有 ( )
①0.25的平方根是0.5
②-0.5的平方 根是-0.25
③只有正数才有平方根
④0的平方根是0CA. 1个 B. 2个. C. 3个 D. 4个正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。a的一个平方根是3,则另一个平方根是 ,a= 。-393a-22和2a-3是m的两个平方根,
试求m的值。正数a的正的平方根叫做a的算术平方根。正数a的算术平方根记作:它的另一个平方根记作:一个正数a的平方根表示为:0的算术平方根还是0说明:这样求一个正数的平方根,只要求出它的算术平方根后,就可以写出它的平方根了。想一想 “负数没有平方根”与“一个数的平方根不能为负数”意义是否一样? 求一个数的平方根(二次方根)的运算,叫做开平方,开平方运算的结果就是平方根。平方与开平方是互为逆运算.举一个实际例子吧!5 的平方根,可以记作 和- ,或± 注意:因为负数没有平方根,所以在式子
中的被开方数 a ≥0 ,否则式子 没有意义。即式子 中的 a 是一个非负数。 例1:判断下列各数有没有平方根,如果有平方根,试求出它的平方根;如果没有平方根,说明理由。(1)81;
(2)-81;
(3)0;
(4) ;
(5) 。 例2:求下列各数的平方根。(1)100;(2)1.44;(3) ;(4)解: (1)∴100的平方根是±10即注意:不能写成请你妨照上面的例子完成其余三个小题。……请谈谈你的收获学习小结:本节课我们学习了哪些内容,你能回答吗?1.平方根的概念:一个数的平方等于a,这个数叫做a的平方根.2.平方根的性质:一个正数的平方根有两个,它们互为相反数.0的平方根还是0.负数没有平方根.3.平方根的表示法:4.算术平方根的概念:正数a的正的平方根叫做a的算术平方根比一比看谁最聪明?如图,求左圈和右圈中的表示的数:?练一练:
求出下列各数的平方根(1)225(2)(3)6.25(4)用计算器求下列各数的算术平方根(1) 529; (2)1225; (3)44.81思考: 你能求出下列各式中的未知数x吗?
(1) x2=49
(2)(x-1)2=25想一想判断下列说法是否正确.1. 的平方根是±16. ( ) 2. 一定是正数. ( )3.a2的算术平方根是a. ( )4.若 ,则a=-5. ( )5. . ( )6.-6是(-6)2的平方根. ( )7.若x2=36,则x= ( ) 8.如果两个数平方后相等,那么它们的也相等×××××√√例2. 已知 有意义,则x一定是 ( )
A.正数 B. 负数 C. 非负数 D. 非正数例3.求下列各式的值例3. 求使 有意义x的取值范围.例4.已知a、b满足等式 +︱b+5︱=0, 求a2-12b的算术平方根.X≤0补充练习;213256≥0-5互为相反数我们已学习了3种非负数,即绝对值、偶数次方、算术平方根。几个非负数的和为零,它们就同时为零,然后转化为方程(或方程组)来解。补充练习:练习:国际比赛的足球场的长在100m到110m之间,宽在64m到75m之间,现有一个长方形的足球场其长是宽的1.5倍,面积为7560m2,问:这个足球场能用作国际比赛吗?课本P76习题13.1第9题、第10题.
今 日 作 业
