2022-2023学年北师大版七年级数学上册4.2比较线段的长短 教案
文档属性
| 名称 | 2022-2023学年北师大版七年级数学上册4.2比较线段的长短 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-21 00:00:00 | ||
图片预览


文档简介
第四章 基本平面图形
2 比较线段的长短
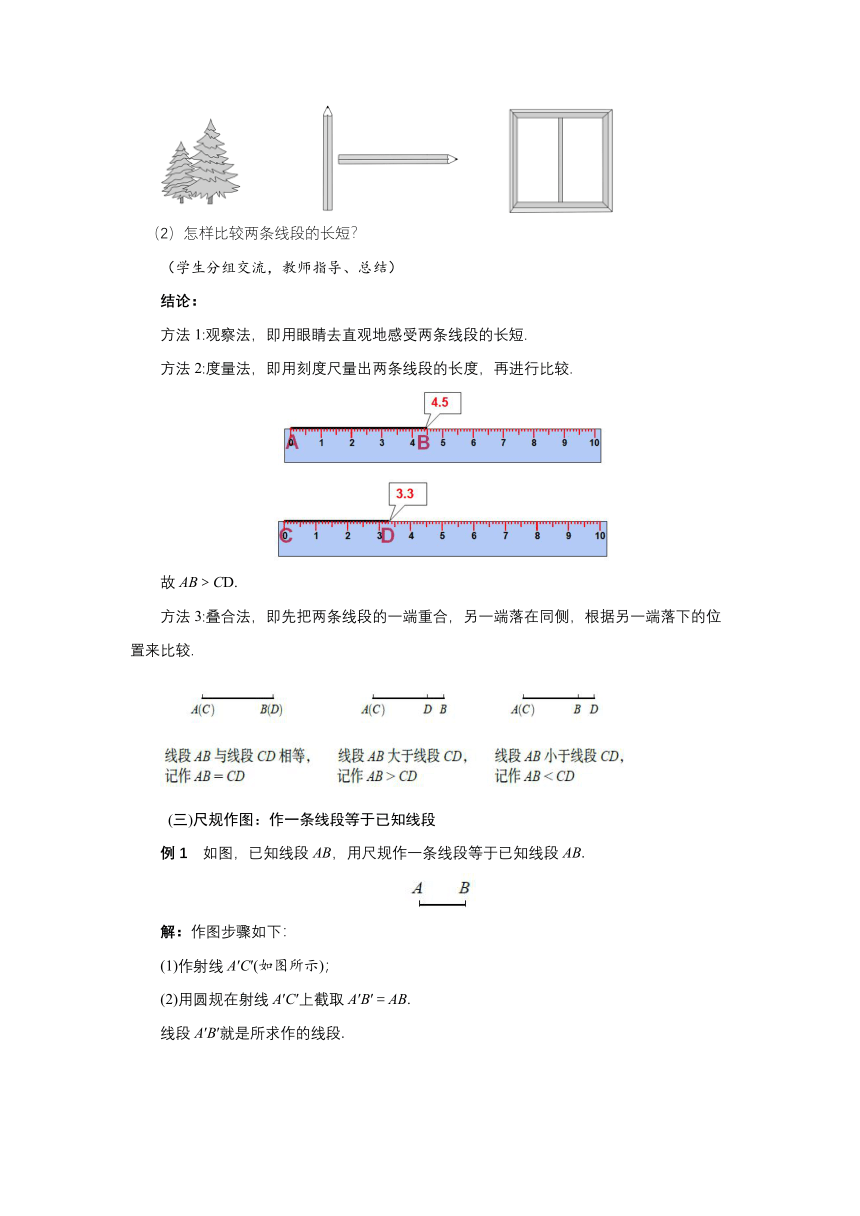
教学目标 1.借助具体情境,了解“两点之间的所有连线中,线段最短”的性质. 2.能借助直尺、圆规等工具比较两条线段的长短. 3.能用直尺和圆规作一条线段等于已知线段. 教学重难点 重点:线段长短的比较方法,线段中点. 难点:线段的中点及线段长短的比较. 教学过程 导入新课 猜测:从A到C有四条道路,哪条路最近? 探究新知 (一) 线段的性质 问题:对于引入问题,根据生活经验可知沿着线段AC走最近.这说明了什么道理? 结论:两点之间的所有连线中,线段最短. 这一事实可以简述为:两点之间,线段最短. 我们把两点之间线段的长度,叫做这两点之间的距离. 说明:线段是一个几何图形,而距离是长度,为非负数. (二)线段的比较 探究:(1)下图中哪棵树高?哪支铅笔长?窗框相邻的两条边哪条边长?你是怎么比较的? (2)怎样比较两条线段的长短? (学生分组交流,教师指导、总结) 结论: 方法1:观察法,即用眼睛去直观地感受两条线段的长短. 方法2:度量法,即用刻度尺量出两条线段的长度,再进行比较. 故AB>CD. 方法3:叠合法,即先把两条线段的一端重合,另一端落在同侧,根据另一端落下的位置来比较. (三)尺规作图:作一条线段等于已知线段 例1 如图,已知线段AB,用尺规作一条线段等于已知线段AB. 解:作图步骤如下: (1)作射线A′C′(如图所示); (2)用圆规在射线A′C′上截取A′B′=AB. 线段A′B′就是所求作的线段. (四)线段中点及其运用 如图,点M把线段AB分成相等的两条线段AM与MB,点M叫做线段AB的中点. 探究:如图,点M为线段AB的中点,则线段AM、BM、AB间有哪些等量关系 线段中点的几何表示方法: ∵ M为线段AB的中点,∴ AMAB或AB=2AM=2MB. 例2 如图,点C在线段AB上,线段AC8 cm,BC4 cm,M,N分别是AC,BC的中点. (1)求线段MN的长度. (2)设ACBCa cm,其他条件不变,你能猜测出MN的长度吗 请证明你的猜测. 解:(1)∵ M,N分别是AC,BC的中点, ∴ CMAC4 cm,CNBC2 cm, ∴ MNCMCN426(cm). (2)猜测MN = a cm. ∵ M,N分别是AC,BC的中点,∴ CMAC,CNBC, ∴ MNCMCN(ACBC)a cm. 说明:与线段的和、差、中点有关的计算题,应注意数形结合,根据已知条件画出图形再加以分析. 课堂练习 1.下列四个生活现象: ①上体育课时,老师检查队伍是不是一条直线,只要看第一个学生就可以了; ②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线; ③从A地到B地架设电线,总是尽可能沿着线段AB架设; ④把弯曲的公路改直,就能缩短路程. 其中可用“两点之间,线段最短”来解释的现象是( ) A.①② B.①③ C.②④ D.③④ 2.如图,一支水笔正好与一把直尺平靠放在一起,小明发现:水笔的笔尖端(A点)对着直尺的刻度约为5.6 cm,另一端(B点)对着直尺的刻度约为20.6 cm,则水笔的中点位置对着直尺的刻度约为( ) A.15 cm B.7.5 cm C.13.1 cm D.12.1 cm 3.如图,下列说法不能判定点C是线段AB的中点的是( ) A.ACCB B.AB2AC C.ACCBAB D.CBAB 4.如图,延长线段AB到C,使BC=4,若AB=8,则线段AC的长是BC的________倍. 5. 如图,已知B是AC的中点,C是BD的中点,若 BC=2 cm,则AD=________cm. 6.已知线段AB=4 cm,在直线AB上画线段BC3 cm,求AC的长. 参考答案 1.D 2.C 3.C 4.3 5.6 6.解:在“直线AB上画线段BC” ,这意味着要以B为所画线段的一个端点,另一个端点既可能在线段AB上,也可能在线段AB的延长线上. (1)当C在线段AB的延长线上时,ACABBC437(cm); (2)当C在线段AB上时,ACABBC431(cm). 所以AC的长为7 cm或1 cm. 课堂小结 布置作业 完成教材习题4.2. 板书设计 第四章 基本平面图形 2 比较线段的长短 (一)线段的性质 (二)线段的比较 (三)尺规作图:作一条线段等于已知线段 (四)线段中点及其运用 例1 如图,已知线段AB,用尺规作一条线段等于已知线段AB. 例2 如图,点C在线段AB上,线段AC8 cm,BC4 cm,M,N分别是AC,BC的中点. (1)求线段MN的长度. (2)设ACBCa cm,其他条件不变,你能猜测出MN的长度吗 请证明你的猜测.
2 比较线段的长短
教学目标 1.借助具体情境,了解“两点之间的所有连线中,线段最短”的性质. 2.能借助直尺、圆规等工具比较两条线段的长短. 3.能用直尺和圆规作一条线段等于已知线段. 教学重难点 重点:线段长短的比较方法,线段中点. 难点:线段的中点及线段长短的比较. 教学过程 导入新课 猜测:从A到C有四条道路,哪条路最近? 探究新知 (一) 线段的性质 问题:对于引入问题,根据生活经验可知沿着线段AC走最近.这说明了什么道理? 结论:两点之间的所有连线中,线段最短. 这一事实可以简述为:两点之间,线段最短. 我们把两点之间线段的长度,叫做这两点之间的距离. 说明:线段是一个几何图形,而距离是长度,为非负数. (二)线段的比较 探究:(1)下图中哪棵树高?哪支铅笔长?窗框相邻的两条边哪条边长?你是怎么比较的? (2)怎样比较两条线段的长短? (学生分组交流,教师指导、总结) 结论: 方法1:观察法,即用眼睛去直观地感受两条线段的长短. 方法2:度量法,即用刻度尺量出两条线段的长度,再进行比较. 故AB>CD. 方法3:叠合法,即先把两条线段的一端重合,另一端落在同侧,根据另一端落下的位置来比较. (三)尺规作图:作一条线段等于已知线段 例1 如图,已知线段AB,用尺规作一条线段等于已知线段AB. 解:作图步骤如下: (1)作射线A′C′(如图所示); (2)用圆规在射线A′C′上截取A′B′=AB. 线段A′B′就是所求作的线段. (四)线段中点及其运用 如图,点M把线段AB分成相等的两条线段AM与MB,点M叫做线段AB的中点. 探究:如图,点M为线段AB的中点,则线段AM、BM、AB间有哪些等量关系 线段中点的几何表示方法: ∵ M为线段AB的中点,∴ AMAB或AB=2AM=2MB. 例2 如图,点C在线段AB上,线段AC8 cm,BC4 cm,M,N分别是AC,BC的中点. (1)求线段MN的长度. (2)设ACBCa cm,其他条件不变,你能猜测出MN的长度吗 请证明你的猜测. 解:(1)∵ M,N分别是AC,BC的中点, ∴ CMAC4 cm,CNBC2 cm, ∴ MNCMCN426(cm). (2)猜测MN = a cm. ∵ M,N分别是AC,BC的中点,∴ CMAC,CNBC, ∴ MNCMCN(ACBC)a cm. 说明:与线段的和、差、中点有关的计算题,应注意数形结合,根据已知条件画出图形再加以分析. 课堂练习 1.下列四个生活现象: ①上体育课时,老师检查队伍是不是一条直线,只要看第一个学生就可以了; ②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线; ③从A地到B地架设电线,总是尽可能沿着线段AB架设; ④把弯曲的公路改直,就能缩短路程. 其中可用“两点之间,线段最短”来解释的现象是( ) A.①② B.①③ C.②④ D.③④ 2.如图,一支水笔正好与一把直尺平靠放在一起,小明发现:水笔的笔尖端(A点)对着直尺的刻度约为5.6 cm,另一端(B点)对着直尺的刻度约为20.6 cm,则水笔的中点位置对着直尺的刻度约为( ) A.15 cm B.7.5 cm C.13.1 cm D.12.1 cm 3.如图,下列说法不能判定点C是线段AB的中点的是( ) A.ACCB B.AB2AC C.ACCBAB D.CBAB 4.如图,延长线段AB到C,使BC=4,若AB=8,则线段AC的长是BC的________倍. 5. 如图,已知B是AC的中点,C是BD的中点,若 BC=2 cm,则AD=________cm. 6.已知线段AB=4 cm,在直线AB上画线段BC3 cm,求AC的长. 参考答案 1.D 2.C 3.C 4.3 5.6 6.解:在“直线AB上画线段BC” ,这意味着要以B为所画线段的一个端点,另一个端点既可能在线段AB上,也可能在线段AB的延长线上. (1)当C在线段AB的延长线上时,ACABBC437(cm); (2)当C在线段AB上时,ACABBC431(cm). 所以AC的长为7 cm或1 cm. 课堂小结 布置作业 完成教材习题4.2. 板书设计 第四章 基本平面图形 2 比较线段的长短 (一)线段的性质 (二)线段的比较 (三)尺规作图:作一条线段等于已知线段 (四)线段中点及其运用 例1 如图,已知线段AB,用尺规作一条线段等于已知线段AB. 例2 如图,点C在线段AB上,线段AC8 cm,BC4 cm,M,N分别是AC,BC的中点. (1)求线段MN的长度. (2)设ACBCa cm,其他条件不变,你能猜测出MN的长度吗 请证明你的猜测.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
