2022-2023学年北师大版七年级数学上册 4.3角 教案
文档属性
| 名称 | 2022-2023学年北师大版七年级数学上册 4.3角 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-21 20:22:31 | ||
图片预览



文档简介
第四章 基本平面图形
3 角
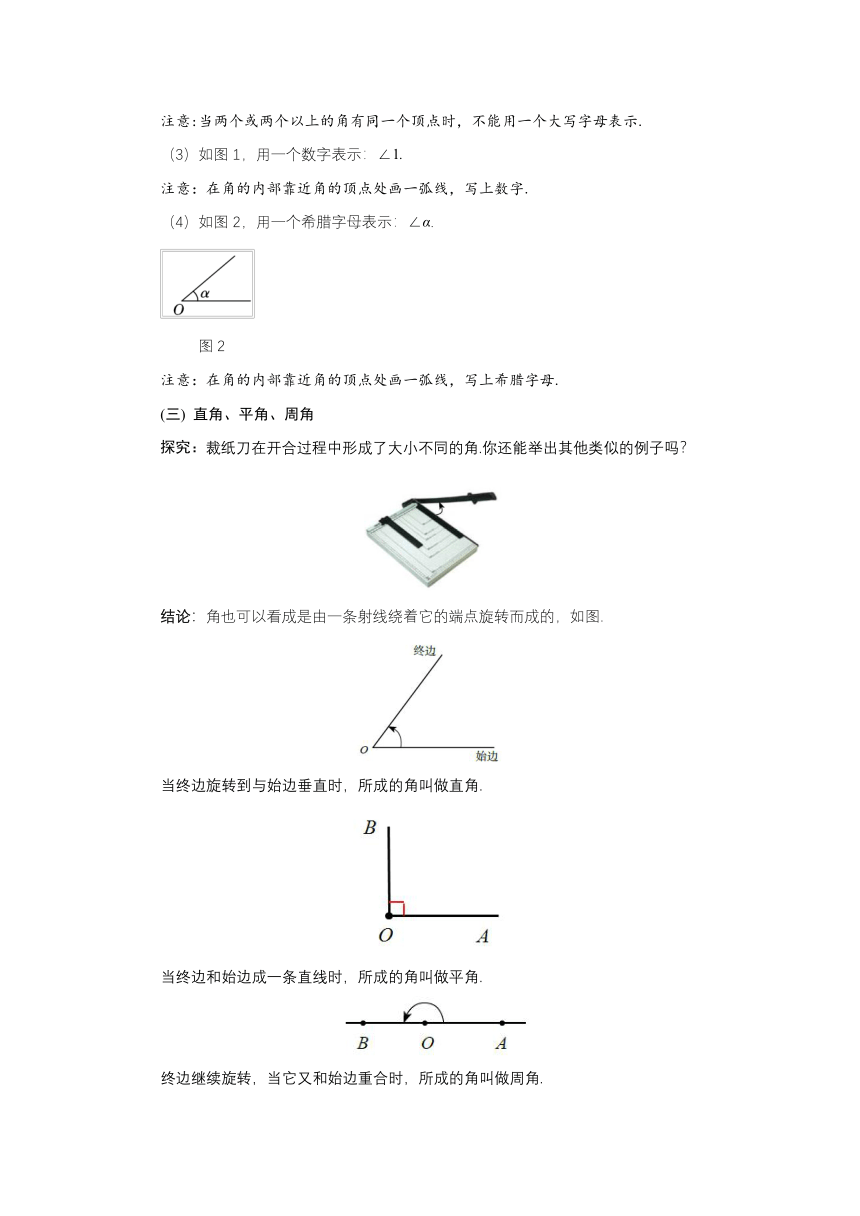
教学目标 1.让学生理解角的定义及有关概念. 2.让学生用运动的观点理解角、直角、平角、周角等概念. 3.使学生掌握角的表示方法. 4.让学生学会度、分、秒的转化和运算. 教学重难点 重点:角的定义及有关概念,角度的测量,以及度、分、秒的互化. 难点:度、分、秒的互化. 教学过程 导入新课 问题1:以前我们曾经认识过角,你们能从这些图形中指出角吗? 问题2:我们已经认识了射线,从一点可以引出多少条射线? 问题3:如果从一点出发任意取两条射线,那出现的是什么图形? (通过后面两个问题,使学生认识到几何图形都是由基本元素构成的,这是建模思想的初步渗透) 探究新知 (一) 角的定义 探究1:学生在练习本上画出一个角,并思考自己是怎样画成一个角的? (教师在黑板上同步演示角的画法,学生归纳、观察后给出角的定义1) 角的定义1:角由两条具有公共端点的射线组成. 探究2:教师拿出教学用的圆规演示角的动态形成过程,从而生成一个角.学生观察、归纳并总结出角的定义2. 角的定义2:角也可以看成是一条射线绕着它的端点旋转而成的. 起始位置的射线叫做这个角的始边; 终止位置的射线叫做这个角的终边. (二)角的表示 探究:如图,(1)用适当的方式分别表示图中的每个角. (2)∠BAC,∠CAD 和 ∠BAD 能用 ∠A 来表示吗? (学生通过观察、分析,进一步掌握角的表示方法) 结论:一个角可以有以下表示方法: 图1 (1)如图1,用三个大写字母表示:∠AOB 或∠BOA . 注意:顶点的字母必须写在中间. (2)如图1,用一个大写字母表示:∠O . 注意:当两个或两个以上的角有同一个顶点时,不能用一个大写字母表示. (3)如图1,用一个数字表示:∠1. 注意:在角的内部靠近角的顶点处画一弧线,写上数字. (4)如图2,用一个希腊字母表示:∠α. 图2 注意:在角的内部靠近角的顶点处画一弧线,写上希腊字母. (三) 直角、平角、周角 探究:裁纸刀在开合过程中形成了大小不同的角.你还能举出其他类似的例子吗? 结论:角也可以看成是由一条射线绕着它的端点旋转而成的,如图. 当终边旋转到与始边垂直时,所成的角叫做直角. 当终边和始边成一条直线时,所成的角叫做平角. 终边继续旋转,当它又和始边重合时,所成的角叫做周角. 一个直角90°,一个平角180°, 一个周角360°. 例1 下列说法正确的是 ( ) A.平角就是一条直线 B.周角就是一条射线 C.小于平角的角是钝角 D.一个周角的度数等于四个直角的度数和 解析:平角不是一条直线,故A错;角和射线不是一个概念,故B错;小于平角的角不一定是钝角,还可能是直角和锐角,故C错;一个周角360°,一个直角90°,故D正确. 答案:D (四) 角度的换算 把一个周角分成360等份,每一份就是1度的角,记作1°. 把1°的角分成60等份,每一份叫做1分的角,记作1′. 把1′ 的角分成60等份,每一份叫做1秒的角,记作1″. 所以,角的度、分、秒是60进制的,这和时间的时、分、秒是一样的. 1°的 为1分,记作1′,1°=60′. 1′的为1秒,记作1″,即1′=60″. 例2 (1)把25.72°用度、分、秒表示; (2)把45°12′30″化成度. 解: (1)0.72°0.72×60′43.2′,0.2′0.2×60″12″, ∴ 25.72°25°43′12″. (2)30″30×′0.5′,12.5′12.5×°≈0.21°, ∴ 45°12′30″45.21°. 总结:(1)是由高级单位向低级单位化;(2)是由低级单位向高级单位化.它们都必须是逐级进行的,“越级”化单位容易出错,转化时,要熟记它们之间的换算关系,将度、分、秒化为度的一般公式为a°b′c″°. (五) 角的度量 阅读并完成课本第116页做一做. (学生自主完成,教师指导总结) 角的度量步骤: (1)对中:顶点对中心. (2)对线:一边与刻度尺的零度线重合. (3)读数. 课堂练习 1.下列语句正确的是( ) A.两条直线相交,组成的图形叫做角 B.两条有公共端点的线段组成的图形叫角 C.两条有公共点的射线组成的图形叫角 D.从同一点引出的两条射线组成的图形叫角 2.下列说法正确的是( ) A.平角是一条直线 B.一条射线是一个周角 C.两条射线组成的图形叫做角 D.两边成一直线的角是平角 3. 下列四个图中,能用∠1、∠AOB、∠O三种方法表示同一个角的是( ) A B C D 4.(1)131°28′﹣51°32′15″ . (2)58°38′27″47°42′40″ . 5.(1)用度、分、秒表示48.26°; (2)用度表示37°24′36″; (3)42°16′18°23′×2; (4)90°19°12′÷6. 6. 某火车站的钟楼上装有一个电子报时钟,在钟面的边界上,每一分钟的刻度处都装有一只小彩灯. (1)晚上9时30分时,时针与分针所夹的角内有多少只小彩灯(包括分针处的彩灯) (2)晚上9时35分20秒,时针与分针所夹的角内有多少只小彩灯 参考答案 1.D 2.D 3.D 4.(1)79°55′45″ (2)106°21′7″ 5. 解:(1)48.26° 48°0.26×60′ 48°15′0.6×60″ 48°15′36″; (2)根据1°60′,1′60″得, 36″÷600.6′,24.6′÷600.41°, 所以37°24′36″用度来表示为37.41°; (3)42°16′18°23′×2 42°16′36°46′ 78°62′ 79°2′; (4)90°19°12′÷6 90°18°72′÷6 90°3°12′ 86°48′. 6. 解:(1)晚上9时30分时,时针与分针之间有3017.5(个)小格,中间有17个分钟刻度,而每一个分钟刻度处装有一只小彩灯,连同分针处的彩灯,时针与分针所夹的角内共有18只小彩灯. (2)晚上9时35分20秒,时针与分针之间有(个)小格,中间有12个分钟刻度,而每一个分钟刻度处装有一只小彩灯,所以晚上9时35分20秒时,时针与分针所夹的角内有12只小彩灯. 课堂小结 布置作业 完成教材习题4.3. 板书设计 第四章 基本平面图形 3 角 (一) 角的定义 角的定义1:角是两条具有公共端点的射线所组成的图形 角的定义2:角也可以看成是由一条射线绕着它的端点旋转而成的图形 (二)角的表示 (1)用三个大写字母表示; (2)用一个大写字母表示; (3)用一个数字表示; (4)用一个希腊字母表示. (三) 直角、平角、周角 (四) 角度的换算 1°的 为1分,记作1′,即1°=60′. 1′的为1秒,记作1″,即1′=60″. (五) 角的度量
3 角
教学目标 1.让学生理解角的定义及有关概念. 2.让学生用运动的观点理解角、直角、平角、周角等概念. 3.使学生掌握角的表示方法. 4.让学生学会度、分、秒的转化和运算. 教学重难点 重点:角的定义及有关概念,角度的测量,以及度、分、秒的互化. 难点:度、分、秒的互化. 教学过程 导入新课 问题1:以前我们曾经认识过角,你们能从这些图形中指出角吗? 问题2:我们已经认识了射线,从一点可以引出多少条射线? 问题3:如果从一点出发任意取两条射线,那出现的是什么图形? (通过后面两个问题,使学生认识到几何图形都是由基本元素构成的,这是建模思想的初步渗透) 探究新知 (一) 角的定义 探究1:学生在练习本上画出一个角,并思考自己是怎样画成一个角的? (教师在黑板上同步演示角的画法,学生归纳、观察后给出角的定义1) 角的定义1:角由两条具有公共端点的射线组成. 探究2:教师拿出教学用的圆规演示角的动态形成过程,从而生成一个角.学生观察、归纳并总结出角的定义2. 角的定义2:角也可以看成是一条射线绕着它的端点旋转而成的. 起始位置的射线叫做这个角的始边; 终止位置的射线叫做这个角的终边. (二)角的表示 探究:如图,(1)用适当的方式分别表示图中的每个角. (2)∠BAC,∠CAD 和 ∠BAD 能用 ∠A 来表示吗? (学生通过观察、分析,进一步掌握角的表示方法) 结论:一个角可以有以下表示方法: 图1 (1)如图1,用三个大写字母表示:∠AOB 或∠BOA . 注意:顶点的字母必须写在中间. (2)如图1,用一个大写字母表示:∠O . 注意:当两个或两个以上的角有同一个顶点时,不能用一个大写字母表示. (3)如图1,用一个数字表示:∠1. 注意:在角的内部靠近角的顶点处画一弧线,写上数字. (4)如图2,用一个希腊字母表示:∠α. 图2 注意:在角的内部靠近角的顶点处画一弧线,写上希腊字母. (三) 直角、平角、周角 探究:裁纸刀在开合过程中形成了大小不同的角.你还能举出其他类似的例子吗? 结论:角也可以看成是由一条射线绕着它的端点旋转而成的,如图. 当终边旋转到与始边垂直时,所成的角叫做直角. 当终边和始边成一条直线时,所成的角叫做平角. 终边继续旋转,当它又和始边重合时,所成的角叫做周角. 一个直角90°,一个平角180°, 一个周角360°. 例1 下列说法正确的是 ( ) A.平角就是一条直线 B.周角就是一条射线 C.小于平角的角是钝角 D.一个周角的度数等于四个直角的度数和 解析:平角不是一条直线,故A错;角和射线不是一个概念,故B错;小于平角的角不一定是钝角,还可能是直角和锐角,故C错;一个周角360°,一个直角90°,故D正确. 答案:D (四) 角度的换算 把一个周角分成360等份,每一份就是1度的角,记作1°. 把1°的角分成60等份,每一份叫做1分的角,记作1′. 把1′ 的角分成60等份,每一份叫做1秒的角,记作1″. 所以,角的度、分、秒是60进制的,这和时间的时、分、秒是一样的. 1°的 为1分,记作1′,1°=60′. 1′的为1秒,记作1″,即1′=60″. 例2 (1)把25.72°用度、分、秒表示; (2)把45°12′30″化成度. 解: (1)0.72°0.72×60′43.2′,0.2′0.2×60″12″, ∴ 25.72°25°43′12″. (2)30″30×′0.5′,12.5′12.5×°≈0.21°, ∴ 45°12′30″45.21°. 总结:(1)是由高级单位向低级单位化;(2)是由低级单位向高级单位化.它们都必须是逐级进行的,“越级”化单位容易出错,转化时,要熟记它们之间的换算关系,将度、分、秒化为度的一般公式为a°b′c″°. (五) 角的度量 阅读并完成课本第116页做一做. (学生自主完成,教师指导总结) 角的度量步骤: (1)对中:顶点对中心. (2)对线:一边与刻度尺的零度线重合. (3)读数. 课堂练习 1.下列语句正确的是( ) A.两条直线相交,组成的图形叫做角 B.两条有公共端点的线段组成的图形叫角 C.两条有公共点的射线组成的图形叫角 D.从同一点引出的两条射线组成的图形叫角 2.下列说法正确的是( ) A.平角是一条直线 B.一条射线是一个周角 C.两条射线组成的图形叫做角 D.两边成一直线的角是平角 3. 下列四个图中,能用∠1、∠AOB、∠O三种方法表示同一个角的是( ) A B C D 4.(1)131°28′﹣51°32′15″ . (2)58°38′27″47°42′40″ . 5.(1)用度、分、秒表示48.26°; (2)用度表示37°24′36″; (3)42°16′18°23′×2; (4)90°19°12′÷6. 6. 某火车站的钟楼上装有一个电子报时钟,在钟面的边界上,每一分钟的刻度处都装有一只小彩灯. (1)晚上9时30分时,时针与分针所夹的角内有多少只小彩灯(包括分针处的彩灯) (2)晚上9时35分20秒,时针与分针所夹的角内有多少只小彩灯 参考答案 1.D 2.D 3.D 4.(1)79°55′45″ (2)106°21′7″ 5. 解:(1)48.26° 48°0.26×60′ 48°15′0.6×60″ 48°15′36″; (2)根据1°60′,1′60″得, 36″÷600.6′,24.6′÷600.41°, 所以37°24′36″用度来表示为37.41°; (3)42°16′18°23′×2 42°16′36°46′ 78°62′ 79°2′; (4)90°19°12′÷6 90°18°72′÷6 90°3°12′ 86°48′. 6. 解:(1)晚上9时30分时,时针与分针之间有3017.5(个)小格,中间有17个分钟刻度,而每一个分钟刻度处装有一只小彩灯,连同分针处的彩灯,时针与分针所夹的角内共有18只小彩灯. (2)晚上9时35分20秒,时针与分针之间有(个)小格,中间有12个分钟刻度,而每一个分钟刻度处装有一只小彩灯,所以晚上9时35分20秒时,时针与分针所夹的角内有12只小彩灯. 课堂小结 布置作业 完成教材习题4.3. 板书设计 第四章 基本平面图形 3 角 (一) 角的定义 角的定义1:角是两条具有公共端点的射线所组成的图形 角的定义2:角也可以看成是由一条射线绕着它的端点旋转而成的图形 (二)角的表示 (1)用三个大写字母表示; (2)用一个大写字母表示; (3)用一个数字表示; (4)用一个希腊字母表示. (三) 直角、平角、周角 (四) 角度的换算 1°的 为1分,记作1′,即1°=60′. 1′的为1秒,记作1″,即1′=60″. (五) 角的度量
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
