24.2.1点和圆的位置关系(1) 课件(共28张PPT)
文档属性
| 名称 | 24.2.1点和圆的位置关系(1) 课件(共28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-20 18:16:56 | ||
图片预览



文档简介
(共28张PPT)
人教版 九年级上册
24.2.1点和圆的位置关系(1)
点和圆、直线和圆、圆和圆的位置关系是学习圆的重要内容之一,它们都是在学习了圆的有关概念和性质后,进一步研究两个图形之间的位置关系.在研究点和圆的位置关系时,是从其几何特征(交点个数)和代数特性(点到圆心的距离与半径的关系)两个角度刻画的.因此,在与圆有关的位置中,点和圆的位置关系是基础.
对于经过不在同一直线上的三点作圆的问题,可以从过一点、过两点开始探究,其中体现了转化的思想.同时,对过一点、过两点、过不同直线上的三点作圆的探究,其核心都是要明确确定圆的要素——确定圆心和半径.
课件说明
学习目标: 1.理解点和圆的三种位置关系,并会运用它解决一 些实际问题; 2.会过不在同一直线上的三个点作圆,理解三角形
的外心和外接圆的概念; 3.结合本节内容的学习,体会数形结合、分类讨论 的数学思想.
学习重点: 点和圆的位置关系.
课件说明
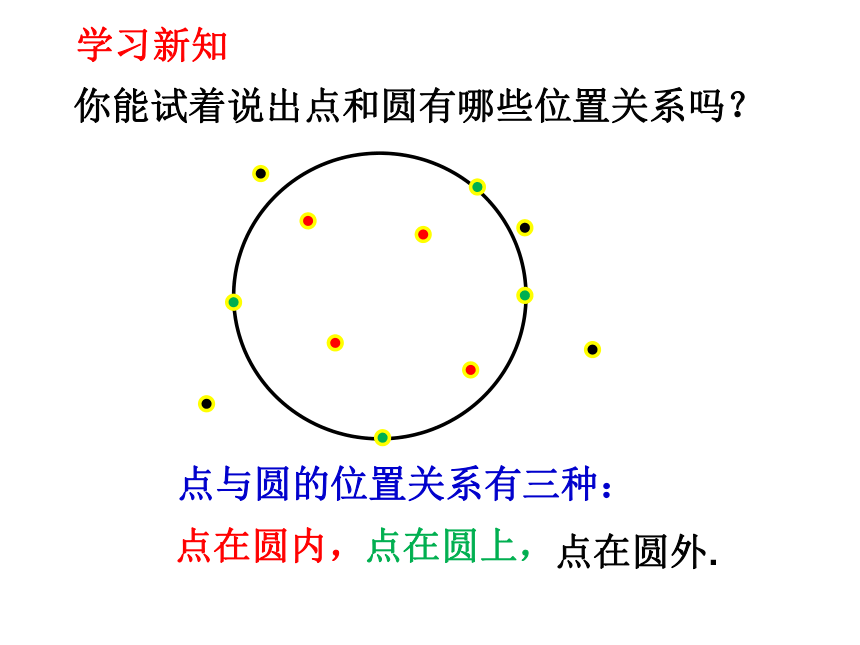
点与圆的位置关系有三种:
你能试着说出点和圆有哪些位置关系吗?
点在圆内,
点在圆上,
点在圆外.
学习新知
如图,设⊙O 的半径为r,
OC>r.
A
B
C
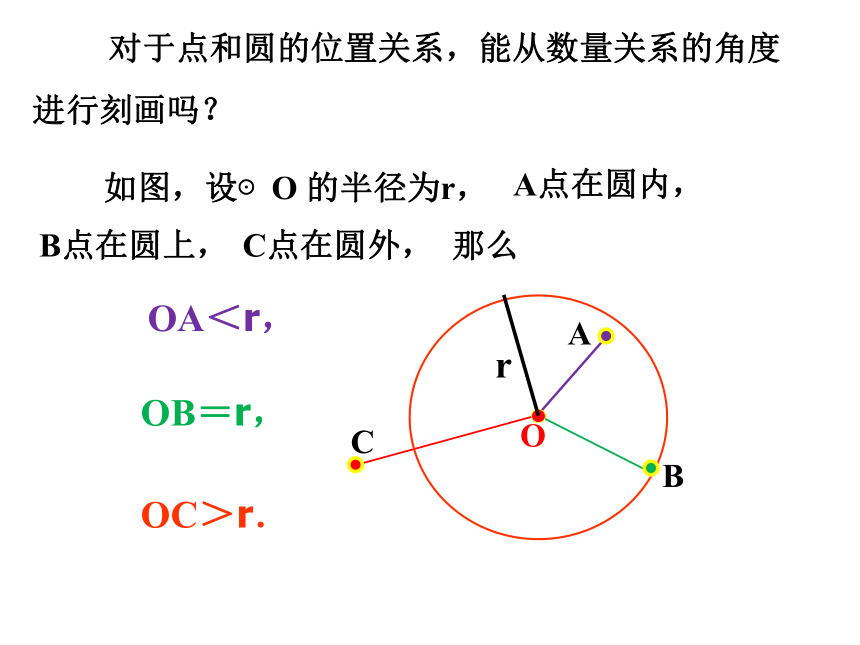
对于点和圆的位置关系,能从数量关系的角度进行刻画吗?
OA<r,
OB=r,
r
A点在圆内,
B点在圆上,
C点在圆外,
那么
O
如图,设⊙O 的半径为r.
OC>r.
A
B
C
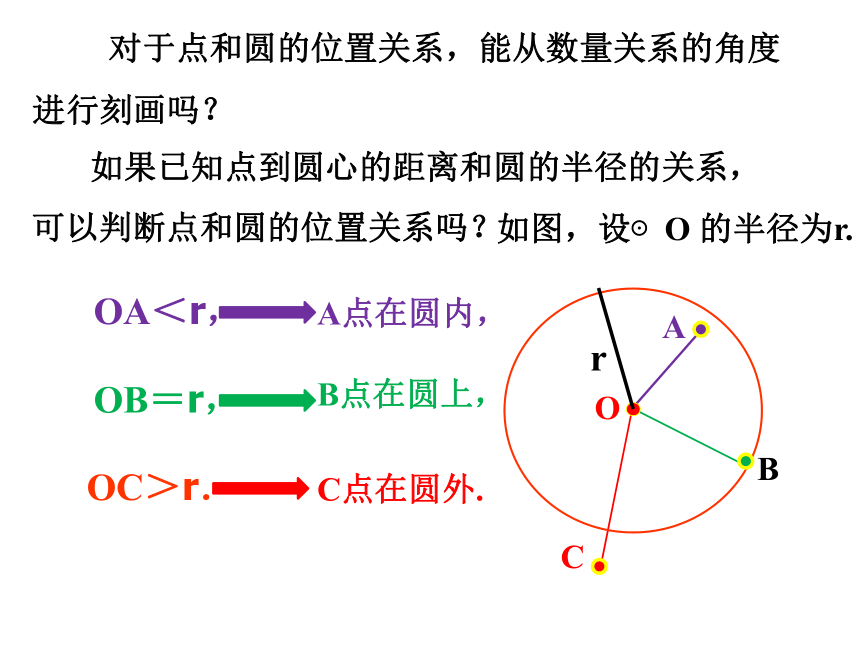
对于点和圆的位置关系,能从数量关系的角度进行刻画吗?
OA<r,
OB=r,
r
A点在圆内,
B点在圆上,
C点在圆外.
如果已知点到圆心的距离和圆的半径的关系,可以判断点和圆的位置关系吗?
O
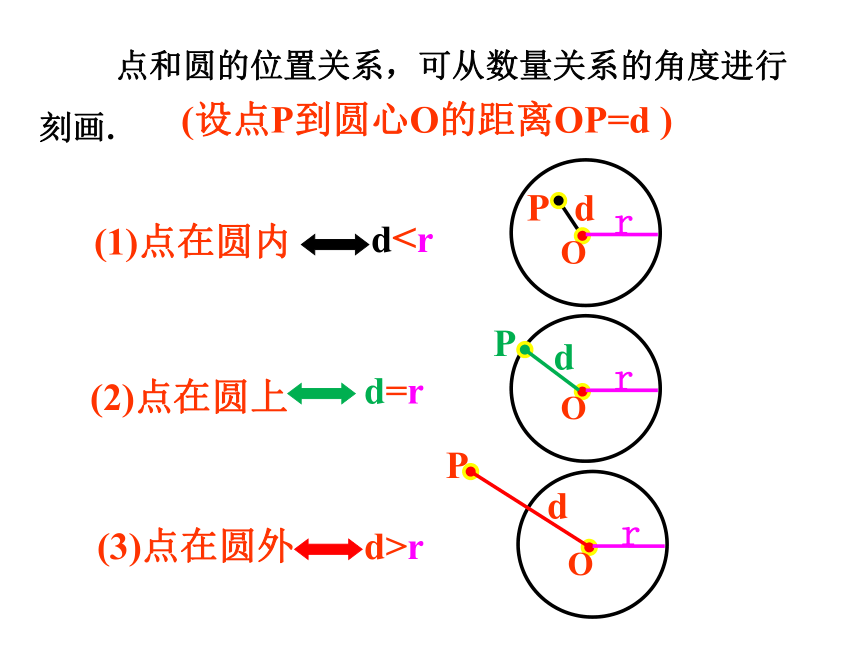
点和圆的位置关系,可从数量关系的角度进行刻画.
dd=r
d>r
(1)点在圆内
(2)点在圆上
(3)点在圆外
(设点P到圆心O的距离OP=d )
O
r
P
d
O
r
O
r
P
d
P
d
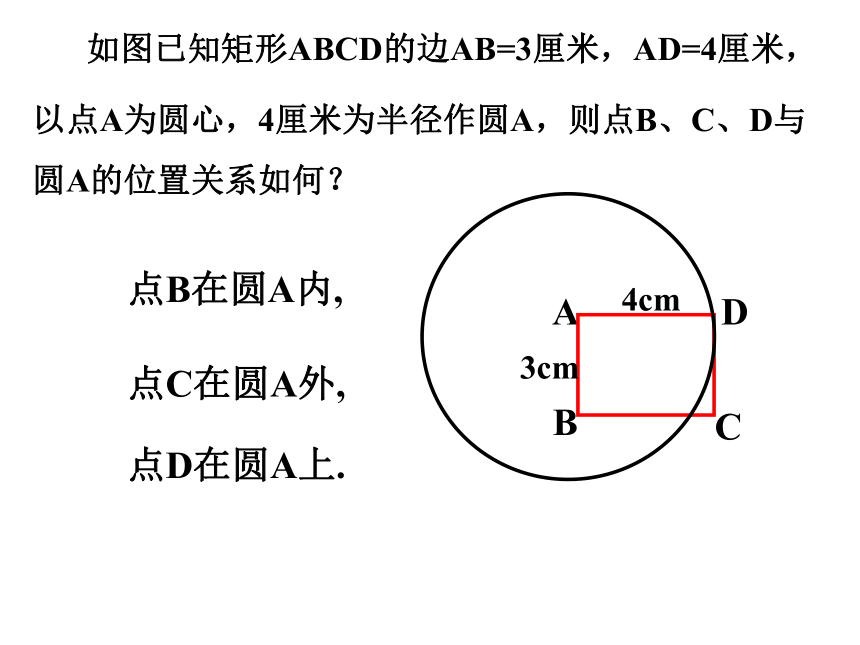
如图已知矩形ABCD的边AB=3厘米,AD=4厘米,
A
D
C
B
以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
点B在圆A内,
点C在圆A外,
点D在圆A上.
3cm
4cm
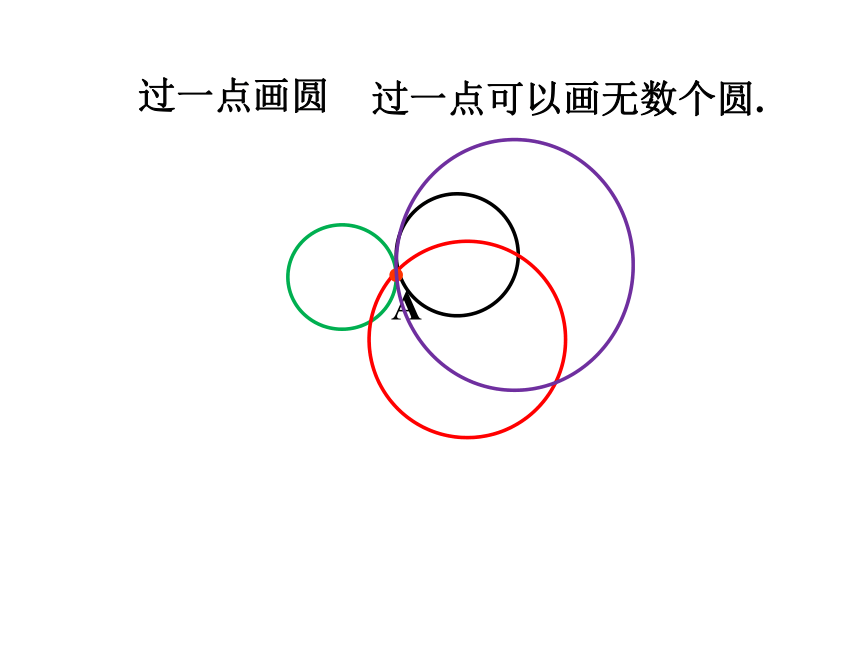
过一点画圆
A
过一点可以画无数个圆.
A
B
所有经A,B两点的圆的圆心都在线段AB的垂直平分线上.
l
过两点画圆
过两点可以画无数个圆.
A
B
C
已知点 A、B、C
已知三点共线
已知三点不共线
过三点画圆
A
B
C
┓
●
●C
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
┏
●
经过A,B,C三点的圆的圆心应该这两条垂直平分线的交点O的位置.
●
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
过不在同一直线上三点画圆
O
A
B
② 分别作线段 AB、BC 的垂直平分线DE 和 FG,DE 和FG 相交于点 O;
① 连接 AB、BC;
O
A
B
C
D
E
F
G
如何经过不在同一条直线上的三个点 A、B、C 作圆?
③ 以点O 为圆心,
OA 为半径作圆.
⊙O 就是所要求作的圆.
A
A
B
C
经过三角形三个顶点可以画一个圆,并且只能画一个.
经过在三角形三个顶点的圆叫做三角形的外接圆.
三角形外接圆的圆心叫做三角形的外心.
这个三角形叫做这个圆的内接三角形.
三角形的外心就是三角形三条边垂直平分线的交点.
O
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
锐角三角形的外心位于三角形内,
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
1.经过三个点一定可以作圆.
2.任意一个三角形一定有一个外接圆.
3.任意一个圆一定有一内接三角形,并且只有一个内接三角形.
4.三角形的外心到三角形各个顶点的距离都相等.
判断正误
(1)点和圆的位置关系:
设⊙O 的半径为 r,点 P 到圆心的距离为 d,则
点 P 在圆外 d>r;
点 P 在圆上 d=r;
点 P 在圆内 d<r.
(2)不在同一条直线上的三个点确定一个圆.
(3)理解三角形外接圆和三角形外心的概念.
小结
1.已知⊙O的半径是4cm,点A 到圆心 O的距离
OA=3cm ,则点 A与⊙O的位置关系是 ( ).
A.点 A在⊙O上 B.点A 在⊙O内
C.点A 在⊙O 外 D.点 A与圆心O 重合
B
巩固新知
2.已知⊙O的半径是 6cm,点P为线段OA的中
点 ,若点 P在⊙O上,则OA的长是 ( ).
A. 等于6cm B.等于12cm
C.大于12cm D.小于6cm
B
3.已知点P到⊙O上的的点的最大距离是7cm,
最小距离是1cm,则⊙O的半径是 ( ).
A. 4cm B.3cm
C.4cm或 3cm D.6cm或3cm
直径是圆中最长的弦
●O
P
A
B
●O
P
A
B
①当点P在⊙O内时
②当点P在⊙O外时
C
y
x
O
4.在平面直角坐标系中,有三个点A (1, -3),
B (0, -3),C(2, -3),这三个点 确
定一个圆 .(填“能”或“不能”)
A (1, -3)
B (0, -3)
C (2, -3)
不能
y
x
O
5.在平面直角坐标系中,有三个点A (0, 3),
B (4, 3),C(0, -1),这△ ABC外接圆的
圆心坐标为 .
A (0, 3)
B (4, 3)
C (0, -1)
D (2, 1)
(2, 1)
6.有一残破的圆形轮片,现要修复它,必须找出它所在圆的圆心,请你用尺规作出圆心.
C
O
① 连接 AB;
② 作线段 AB的垂直
平分线CD 交轮片于点 C;
D
③ 连接 BC;
④作线段 BC的垂直平分线MN交CD 于点 O;
M
N
⑤ 点O 就是轮片所在圆的圆心.
A
B
C
7.如图,A、B、C三个点分别表示三个村庄,要建一个5G基站,使三个村庄到5G基站距离相等,则5G基站应建在何处?
O
① 连接 AB、BC;
② 分别作线段 AB、BC
的垂直平分线DE 和 FG,
DE 和FG 相交于点 O;
③ 点O 就是5G基站所建的位置.
D
E
F
G
据说是微软公司面试试题之一
已知:如图,求直角三角形ABC的面积.
D
B
C
A
AB=10
CD=6
S△ ABC =
1
2
AB · CD
=30.
×
这样的直角三角形不存在.
数学花絮
顶点C点到圆心的距离大于半径5,
顶点C点不在圆上
今天作业
课本P102页第8、9题
课本P101页第1题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 九年级上册
24.2.1点和圆的位置关系(1)
点和圆、直线和圆、圆和圆的位置关系是学习圆的重要内容之一,它们都是在学习了圆的有关概念和性质后,进一步研究两个图形之间的位置关系.在研究点和圆的位置关系时,是从其几何特征(交点个数)和代数特性(点到圆心的距离与半径的关系)两个角度刻画的.因此,在与圆有关的位置中,点和圆的位置关系是基础.
对于经过不在同一直线上的三点作圆的问题,可以从过一点、过两点开始探究,其中体现了转化的思想.同时,对过一点、过两点、过不同直线上的三点作圆的探究,其核心都是要明确确定圆的要素——确定圆心和半径.
课件说明
学习目标: 1.理解点和圆的三种位置关系,并会运用它解决一 些实际问题; 2.会过不在同一直线上的三个点作圆,理解三角形
的外心和外接圆的概念; 3.结合本节内容的学习,体会数形结合、分类讨论 的数学思想.
学习重点: 点和圆的位置关系.
课件说明
点与圆的位置关系有三种:
你能试着说出点和圆有哪些位置关系吗?
点在圆内,
点在圆上,
点在圆外.
学习新知
如图,设⊙O 的半径为r,
OC>r.
A
B
C
对于点和圆的位置关系,能从数量关系的角度进行刻画吗?
OA<r,
OB=r,
r
A点在圆内,
B点在圆上,
C点在圆外,
那么
O
如图,设⊙O 的半径为r.
OC>r.
A
B
C
对于点和圆的位置关系,能从数量关系的角度进行刻画吗?
OA<r,
OB=r,
r
A点在圆内,
B点在圆上,
C点在圆外.
如果已知点到圆心的距离和圆的半径的关系,可以判断点和圆的位置关系吗?
O
点和圆的位置关系,可从数量关系的角度进行刻画.
d
d>r
(1)点在圆内
(2)点在圆上
(3)点在圆外
(设点P到圆心O的距离OP=d )
O
r
P
d
O
r
O
r
P
d
P
d
如图已知矩形ABCD的边AB=3厘米,AD=4厘米,
A
D
C
B
以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
点B在圆A内,
点C在圆A外,
点D在圆A上.
3cm
4cm
过一点画圆
A
过一点可以画无数个圆.
A
B
所有经A,B两点的圆的圆心都在线段AB的垂直平分线上.
l
过两点画圆
过两点可以画无数个圆.
A
B
C
已知点 A、B、C
已知三点共线
已知三点不共线
过三点画圆
A
B
C
┓
●
●C
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
┏
●
经过A,B,C三点的圆的圆心应该这两条垂直平分线的交点O的位置.
●
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
过不在同一直线上三点画圆
O
A
B
② 分别作线段 AB、BC 的垂直平分线DE 和 FG,DE 和FG 相交于点 O;
① 连接 AB、BC;
O
A
B
C
D
E
F
G
如何经过不在同一条直线上的三个点 A、B、C 作圆?
③ 以点O 为圆心,
OA 为半径作圆.
⊙O 就是所要求作的圆.
A
A
B
C
经过三角形三个顶点可以画一个圆,并且只能画一个.
经过在三角形三个顶点的圆叫做三角形的外接圆.
三角形外接圆的圆心叫做三角形的外心.
这个三角形叫做这个圆的内接三角形.
三角形的外心就是三角形三条边垂直平分线的交点.
O
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
锐角三角形的外心位于三角形内,
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
1.经过三个点一定可以作圆.
2.任意一个三角形一定有一个外接圆.
3.任意一个圆一定有一内接三角形,并且只有一个内接三角形.
4.三角形的外心到三角形各个顶点的距离都相等.
判断正误
(1)点和圆的位置关系:
设⊙O 的半径为 r,点 P 到圆心的距离为 d,则
点 P 在圆外 d>r;
点 P 在圆上 d=r;
点 P 在圆内 d<r.
(2)不在同一条直线上的三个点确定一个圆.
(3)理解三角形外接圆和三角形外心的概念.
小结
1.已知⊙O的半径是4cm,点A 到圆心 O的距离
OA=3cm ,则点 A与⊙O的位置关系是 ( ).
A.点 A在⊙O上 B.点A 在⊙O内
C.点A 在⊙O 外 D.点 A与圆心O 重合
B
巩固新知
2.已知⊙O的半径是 6cm,点P为线段OA的中
点 ,若点 P在⊙O上,则OA的长是 ( ).
A. 等于6cm B.等于12cm
C.大于12cm D.小于6cm
B
3.已知点P到⊙O上的的点的最大距离是7cm,
最小距离是1cm,则⊙O的半径是 ( ).
A. 4cm B.3cm
C.4cm或 3cm D.6cm或3cm
直径是圆中最长的弦
●O
P
A
B
●O
P
A
B
①当点P在⊙O内时
②当点P在⊙O外时
C
y
x
O
4.在平面直角坐标系中,有三个点A (1, -3),
B (0, -3),C(2, -3),这三个点 确
定一个圆 .(填“能”或“不能”)
A (1, -3)
B (0, -3)
C (2, -3)
不能
y
x
O
5.在平面直角坐标系中,有三个点A (0, 3),
B (4, 3),C(0, -1),这△ ABC外接圆的
圆心坐标为 .
A (0, 3)
B (4, 3)
C (0, -1)
D (2, 1)
(2, 1)
6.有一残破的圆形轮片,现要修复它,必须找出它所在圆的圆心,请你用尺规作出圆心.
C
O
① 连接 AB;
② 作线段 AB的垂直
平分线CD 交轮片于点 C;
D
③ 连接 BC;
④作线段 BC的垂直平分线MN交CD 于点 O;
M
N
⑤ 点O 就是轮片所在圆的圆心.
A
B
C
7.如图,A、B、C三个点分别表示三个村庄,要建一个5G基站,使三个村庄到5G基站距离相等,则5G基站应建在何处?
O
① 连接 AB、BC;
② 分别作线段 AB、BC
的垂直平分线DE 和 FG,
DE 和FG 相交于点 O;
③ 点O 就是5G基站所建的位置.
D
E
F
G
据说是微软公司面试试题之一
已知:如图,求直角三角形ABC的面积.
D
B
C
A
AB=10
CD=6
S△ ABC =
1
2
AB · CD
=30.
×
这样的直角三角形不存在.
数学花絮
顶点C点到圆心的距离大于半径5,
顶点C点不在圆上
今天作业
课本P102页第8、9题
课本P101页第1题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
