24.3正多边形和圆(1)课件(共28张PPT)
文档属性
| 名称 | 24.3正多边形和圆(1)课件(共28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-20 18:22:18 | ||
图片预览





文档简介
(共36张PPT)
人教版 九年级上册
24.3正多边形和圆(1)
正多边形是生活中常见的图形,因此正多边形的有关计算在生活中经常用到.正多边形和圆关系密切,只要把圆分成相等的一些弧,就可以得到这个圆的内接正多边形.
课件说明
学习目标: 理解正多边形和圆的关系,知道把圆分成相等的 一些弧,就可以得到这个圆的内接正多边形; 学习重点:
正多边形的画法.
课件说明
1.等边三角形的边、角各有什么性质?
2.正方形的边、角各有什么性质?
3.什么是正多边形?
复习引入:
1.什么样的图形是正多边形?
各边相等,各角也相等的多边形是正多边形.
正n边形:如果一个正多边形有n条边,那么这个正多边形叫做正n边形.
观察这些图片,你能否看到正多边形?
如何画出一个正多边形呢?
你能否借助圆画出圆内接正三角形?
你能否借助圆画出圆内接正方形?
你能否借助圆画出圆内接正五边形?
你能否借助圆画出圆内接正五边形?
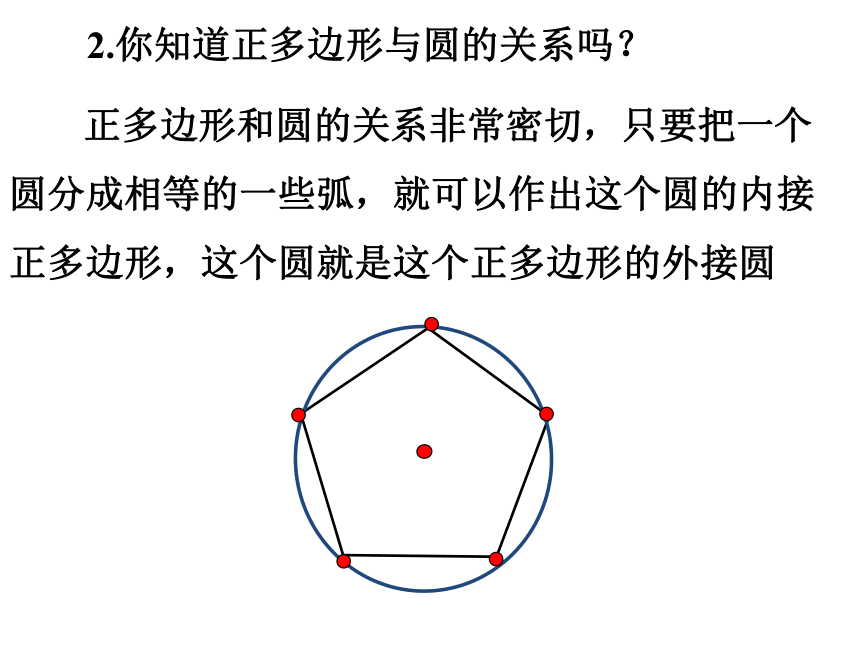
2.你知道正多边形与圆的关系吗?
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆
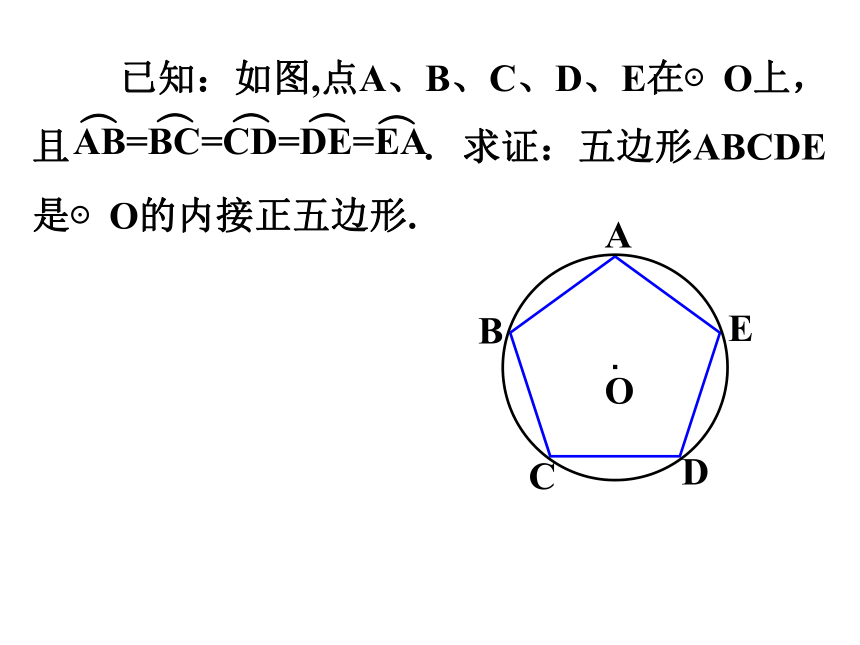
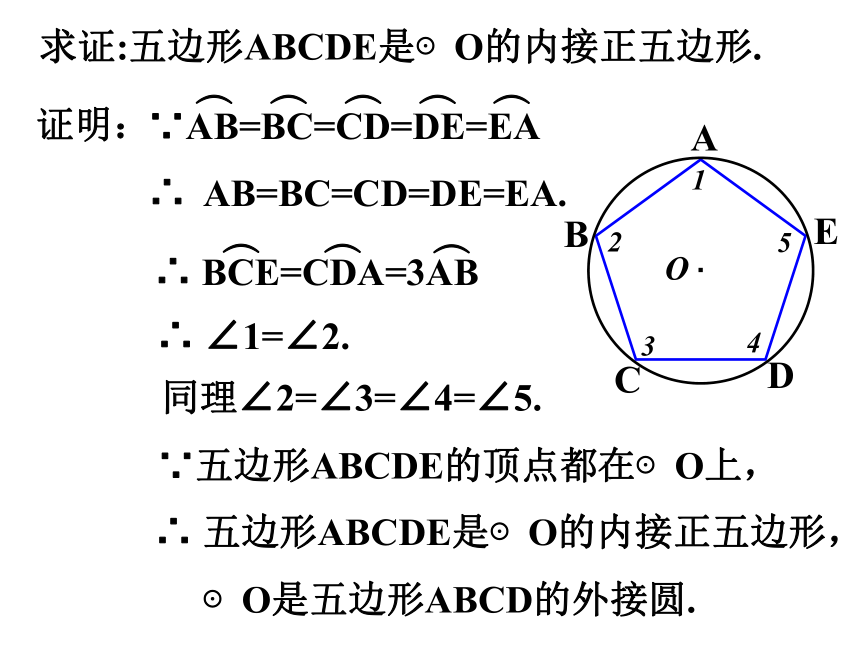
已知:如图,点A、B、C、D、E在⊙O上,且 . 求证:五边形ABCDE是⊙O的内接正五边形.
AB=BC=CD=DE=EA
︵
︵
︵
︵
︵
·
A
B
C
D
E
O
·
A
B
C
D
E
O
∴ AB=BC=CD=DE=EA.
∴ ∠1=∠2.
同理∠2=∠3=∠4=∠5.
∵五边形ABCDE的顶点都在⊙O上,
∴ 五边形ABCDE是⊙O的内接正五边形,
求证:五边形ABCDE是⊙O的内接正五边形.
∵AB=BC=CD=DE=EA
︵
︵
︵
︵
︵
证明:
∴ BCE=CDA=3AB
︵
︵
︵
3
2
1
5
4
⊙O是五边形ABCD的外接圆.
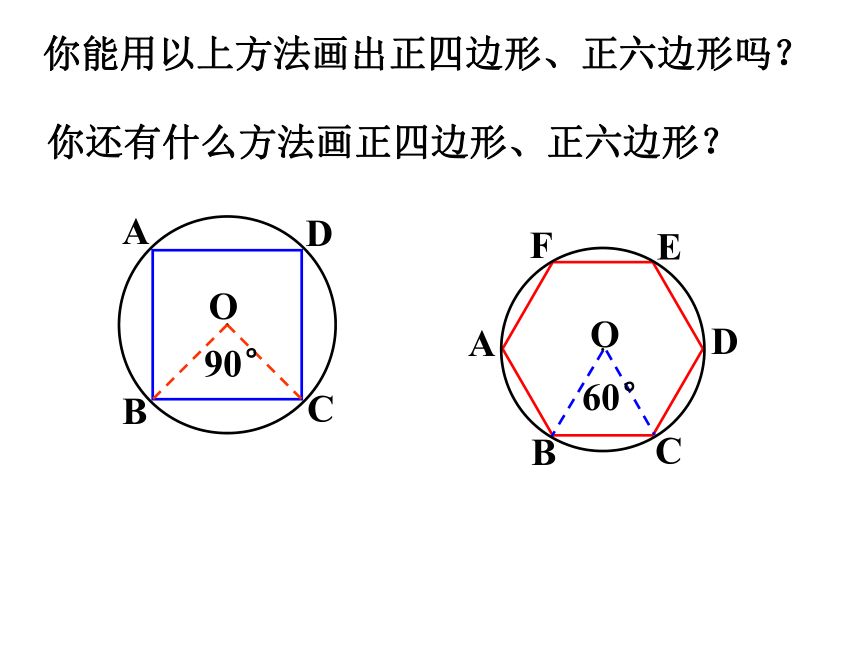
你能用以上方法画出正四边形、正六边形吗?
·
A
B
C
D
O
90°
D
O
A
B
C
E
F
·
60°
你还有什么方法画正四边形、正六边形?
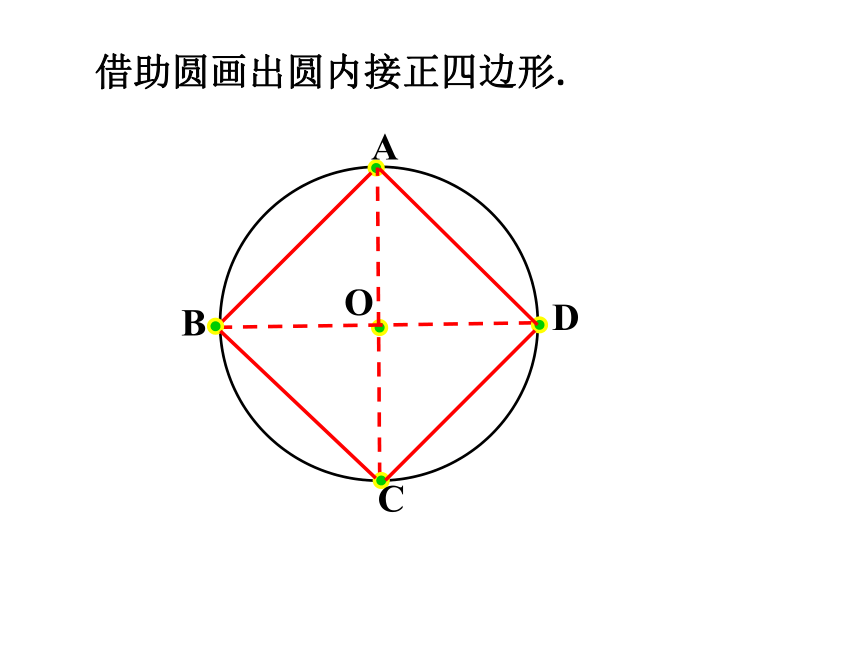
借助圆画出圆内接正四边形.
O
A
B
C
D
借助圆画出圆内接正八边形.
O
A
你能尺规作出正八边形吗?据此你还能作出哪些正多边形?
·
A
B
C
D
O
只要作出已知⊙O的互相垂直的直径即得圆内接正方形,再过圆心作各边的垂线与⊙O相交,或作各中心角的角平分线与⊙O相交,即得圆接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形……
借助圆画出圆内接正六边形.
O
A
B
C
E
D
F
借助圆画出圆内接正三边形.
O
A
B
C
借助圆画出圆内接正十二边形.
O
A
B
C
E
D
F
借助圆画出圆内接正十二边形.
O
A
B
C
E
D
F
G
H
I
K
L
J
你能尺规作出正六边形、正三角形、正十二边形吗?
以半径长在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形………
O
A
B
C
E
D
F
G
H
K
L
J
I
借助圆画出圆内接正五边形.
O
A
B
C
D
M
N
E
借助圆画出圆内接正五边形.
O
A
B
C
D
F
借助圆画出圆内接正五边形.
O
A
B
C
D
F
画出规整的五角星.
A
B
C
已知边长a作正三边形.
① 作线段 AB,使AB=a;
作法:
②分别以点A,B 为圆心,
a为半径作弧,两弧在
AB的同侧交于点C;
③连接 AC、BC, 则△ABC为所求.
B
C
D
已知边长a作正方形.
① 作Rt∠MAN,在AM上截取AD=a,在AN上截取AB=a;
②分别以点D,B 为圆心,
a为半径作弧,两弧在
AB的同侧交于点C;
③连接 DC、BC, 则四边形ABCD为所求.
A
M
N
③分别以点A,B 为圆心,AN为半
径作弧,两弧在交于点D;
C
D
E
A
B
M
N
已知边长a作正五边形.
① 作Rt∠MBA,使AB=a,MB= a;
②连接AM,延长AM至N,使MN=MB;
④分别以点B ,A为圆心,a为半
径作弧,两弧与前两弧交点
分别为C,E;
⑤顺次连接BC,CD,DE,EA,
则五边形ABCDE为所求.
1
2
画正多边形的方法
1.用量角器等分圆
2.尺规作图等分圆
(1)正四、正八边形的尺规作图
(2)正六、正三 、正十二边形的尺规作图
说说作正多边形的方法有哪些
(1)正多边形与圆有什么关系? (2)本节课学习了如何借助圆画正多边形.
小结
正七边形的近似作法
数学花絮
1.作圆O;
2.作直径与圆交于C、D两点;
3.以D为圆心,DO为半径作圆,交圆O于E、F两点;
4.连接E、F,交CD于G;
5.GF或GE就是该圆内接正七边形的边长.
正七边形的近似作法
正九边形的近似作法
1.作圆的垂直中心线AB , CD ;
2.以B 为圆心,BC为半径作圆弧与AB交于点G ;
3.以G为圆心, GC为半径作圆弧交AB于F点;
4.以B为圆心, BF为半径作圆弧交圆周于E点;
5.连接AE ,AE交圆弧CF于H点;
6.连接OH,OH即为内接正九边形的边长.
正九边形的近似作法
数学王子高斯与正十七边形
正十七边形的画法
1.作圆O。
2.作相互垂直的直径AB、CD。
3.作点E,使EO=1/4AO,连结CE。
4.作∠CEB的平分线EF。
5.作∠FEB的平分线EG,交CO于P。
6.作∠GEH=45°,交CD于Q。
7.以CQ为直径作圆,交OB于K。
8.以P为圆心,PK为半径作圆,交CD于L、M。
9.分别过M、L作CD的垂线,交圆O于N、R
10.作弧NR的中点S,以SN为半径将圆O分成17等份。
今天作业
课本P108页习题 24.3第1,6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 九年级上册
24.3正多边形和圆(1)
正多边形是生活中常见的图形,因此正多边形的有关计算在生活中经常用到.正多边形和圆关系密切,只要把圆分成相等的一些弧,就可以得到这个圆的内接正多边形.
课件说明
学习目标: 理解正多边形和圆的关系,知道把圆分成相等的 一些弧,就可以得到这个圆的内接正多边形; 学习重点:
正多边形的画法.
课件说明
1.等边三角形的边、角各有什么性质?
2.正方形的边、角各有什么性质?
3.什么是正多边形?
复习引入:
1.什么样的图形是正多边形?
各边相等,各角也相等的多边形是正多边形.
正n边形:如果一个正多边形有n条边,那么这个正多边形叫做正n边形.
观察这些图片,你能否看到正多边形?
如何画出一个正多边形呢?
你能否借助圆画出圆内接正三角形?
你能否借助圆画出圆内接正方形?
你能否借助圆画出圆内接正五边形?
你能否借助圆画出圆内接正五边形?
2.你知道正多边形与圆的关系吗?
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆
已知:如图,点A、B、C、D、E在⊙O上,且 . 求证:五边形ABCDE是⊙O的内接正五边形.
AB=BC=CD=DE=EA
︵
︵
︵
︵
︵
·
A
B
C
D
E
O
·
A
B
C
D
E
O
∴ AB=BC=CD=DE=EA.
∴ ∠1=∠2.
同理∠2=∠3=∠4=∠5.
∵五边形ABCDE的顶点都在⊙O上,
∴ 五边形ABCDE是⊙O的内接正五边形,
求证:五边形ABCDE是⊙O的内接正五边形.
∵AB=BC=CD=DE=EA
︵
︵
︵
︵
︵
证明:
∴ BCE=CDA=3AB
︵
︵
︵
3
2
1
5
4
⊙O是五边形ABCD的外接圆.
你能用以上方法画出正四边形、正六边形吗?
·
A
B
C
D
O
90°
D
O
A
B
C
E
F
·
60°
你还有什么方法画正四边形、正六边形?
借助圆画出圆内接正四边形.
O
A
B
C
D
借助圆画出圆内接正八边形.
O
A
你能尺规作出正八边形吗?据此你还能作出哪些正多边形?
·
A
B
C
D
O
只要作出已知⊙O的互相垂直的直径即得圆内接正方形,再过圆心作各边的垂线与⊙O相交,或作各中心角的角平分线与⊙O相交,即得圆接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形……
借助圆画出圆内接正六边形.
O
A
B
C
E
D
F
借助圆画出圆内接正三边形.
O
A
B
C
借助圆画出圆内接正十二边形.
O
A
B
C
E
D
F
借助圆画出圆内接正十二边形.
O
A
B
C
E
D
F
G
H
I
K
L
J
你能尺规作出正六边形、正三角形、正十二边形吗?
以半径长在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形………
O
A
B
C
E
D
F
G
H
K
L
J
I
借助圆画出圆内接正五边形.
O
A
B
C
D
M
N
E
借助圆画出圆内接正五边形.
O
A
B
C
D
F
借助圆画出圆内接正五边形.
O
A
B
C
D
F
画出规整的五角星.
A
B
C
已知边长a作正三边形.
① 作线段 AB,使AB=a;
作法:
②分别以点A,B 为圆心,
a为半径作弧,两弧在
AB的同侧交于点C;
③连接 AC、BC, 则△ABC为所求.
B
C
D
已知边长a作正方形.
① 作Rt∠MAN,在AM上截取AD=a,在AN上截取AB=a;
②分别以点D,B 为圆心,
a为半径作弧,两弧在
AB的同侧交于点C;
③连接 DC、BC, 则四边形ABCD为所求.
A
M
N
③分别以点A,B 为圆心,AN为半
径作弧,两弧在交于点D;
C
D
E
A
B
M
N
已知边长a作正五边形.
① 作Rt∠MBA,使AB=a,MB= a;
②连接AM,延长AM至N,使MN=MB;
④分别以点B ,A为圆心,a为半
径作弧,两弧与前两弧交点
分别为C,E;
⑤顺次连接BC,CD,DE,EA,
则五边形ABCDE为所求.
1
2
画正多边形的方法
1.用量角器等分圆
2.尺规作图等分圆
(1)正四、正八边形的尺规作图
(2)正六、正三 、正十二边形的尺规作图
说说作正多边形的方法有哪些
(1)正多边形与圆有什么关系? (2)本节课学习了如何借助圆画正多边形.
小结
正七边形的近似作法
数学花絮
1.作圆O;
2.作直径与圆交于C、D两点;
3.以D为圆心,DO为半径作圆,交圆O于E、F两点;
4.连接E、F,交CD于G;
5.GF或GE就是该圆内接正七边形的边长.
正七边形的近似作法
正九边形的近似作法
1.作圆的垂直中心线AB , CD ;
2.以B 为圆心,BC为半径作圆弧与AB交于点G ;
3.以G为圆心, GC为半径作圆弧交AB于F点;
4.以B为圆心, BF为半径作圆弧交圆周于E点;
5.连接AE ,AE交圆弧CF于H点;
6.连接OH,OH即为内接正九边形的边长.
正九边形的近似作法
数学王子高斯与正十七边形
正十七边形的画法
1.作圆O。
2.作相互垂直的直径AB、CD。
3.作点E,使EO=1/4AO,连结CE。
4.作∠CEB的平分线EF。
5.作∠FEB的平分线EG,交CO于P。
6.作∠GEH=45°,交CD于Q。
7.以CQ为直径作圆,交OB于K。
8.以P为圆心,PK为半径作圆,交CD于L、M。
9.分别过M、L作CD的垂线,交圆O于N、R
10.作弧NR的中点S,以SN为半径将圆O分成17等份。
今天作业
课本P108页习题 24.3第1,6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
