冀教版数学八年级上册同步课件:13.4 三角形的尺规作图(23张PPT)
文档属性
| 名称 | 冀教版数学八年级上册同步课件:13.4 三角形的尺规作图(23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 350.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-20 16:16:22 | ||
图片预览





文档简介
(共23张PPT)
第十三章 全等三角形
13.4 三角形的尺规作图
知识回顾
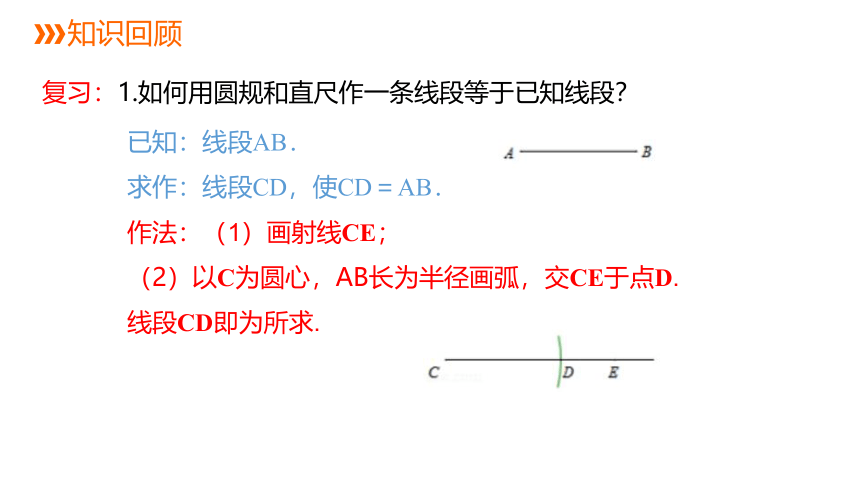
复习:1.如何用圆规和直尺作一条线段等于已知线段?
已知:线段AB.
求作:线段CD,使CD=AB.
作法:(1)画射线CE;
(2)以C为圆心,AB长为半径画弧,交CE于点D.
线段CD即为所求.
已知:∠AOB.
求作:∠A'O'B',使∠A'O'B'=∠AOB.
作法:(1)如图,以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)画一条射线O'A',以点O'为圆心,OC长为半径画弧,交O'A'于点C';
(3)以点C'为圆心,CD长为半径画弧与第二步中所画的弧交于点D′;
(4)过点D'画射线O'B',则∠A'O'B'=∠AOB.
2.如何用圆规和直尺作一个角等于已知角?
问题导入
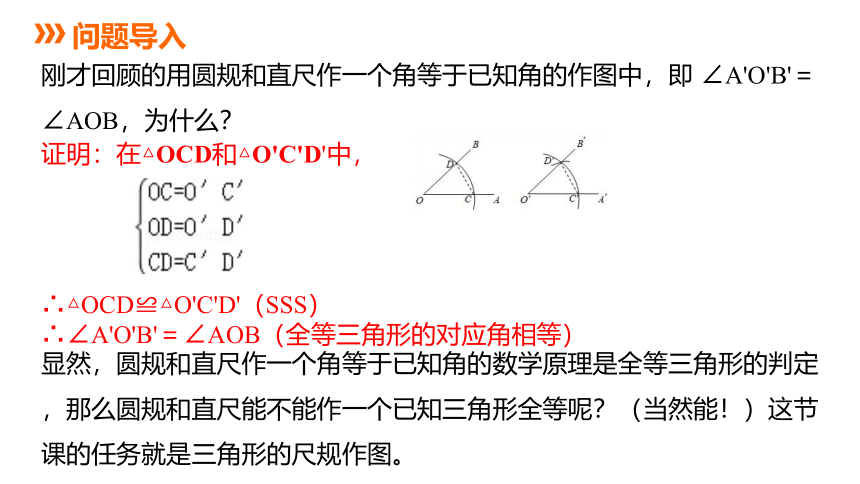
刚才回顾的用圆规和直尺作一个角等于已知角的作图中,即 ∠A'O'B'=∠AOB,为什么?
证明:在△OCD和△O'C'D'中,
∴△OCD≌△O'C'D'(SSS)
∴∠A'O'B'=∠AOB(全等三角形的对应角相等)
显然,圆规和直尺作一个角等于已知角的数学原理是全等三角形的判定,那么圆规和直尺能不能作一个已知三角形全等呢?(当然能!)这节课的任务就是三角形的尺规作图。
获取新知
尺规作图
只用直尺(没有刻度)和圆规也可以画出一些图形,这种画图方法被称为尺规作图.
知识点
概念学习:尺规作图
1
例1 下列作图属于尺规作图的是( )
A.用量角器画出∠AOB的平分线OC
B.借助直尺和圆规作∠AOB,使∠AOB=2∠α
C.画线段AB=3cm
D.用三角尺过点P作AB的垂线
B
例题讲解
解析:根据尺规作图的定义分析即可.
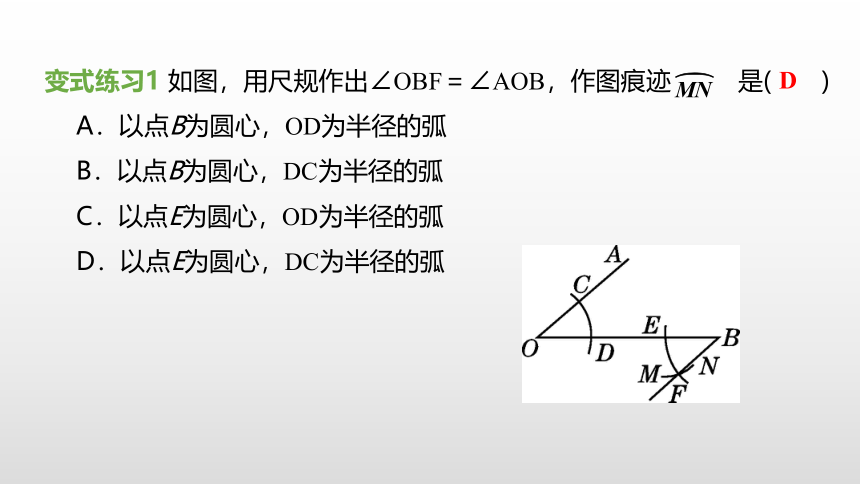
变式练习1 如图,用尺规作出∠OBF=∠AOB,作图痕迹 是( )
A.以点B为圆心,OD为半径的弧
B.以点B为圆心,DC为半径的弧
C.以点E为圆心,OD为半径的弧
D.以点E为圆心,DC为半径的弧
D
例1 如图,已知线段a,b,c.
求作:△ABC,使AB=c,BC=a,AC=b.
解析:由作一条线段等于已知线段,能够作出边AB,即A,B两点确定,而BC=a,AC=b,故以点A为圆心,b为半径画弧长,以点B为圆心,a为半径画弧,两弧的交点就是点C.
例题讲解
知识点
用尺规作三角形
2
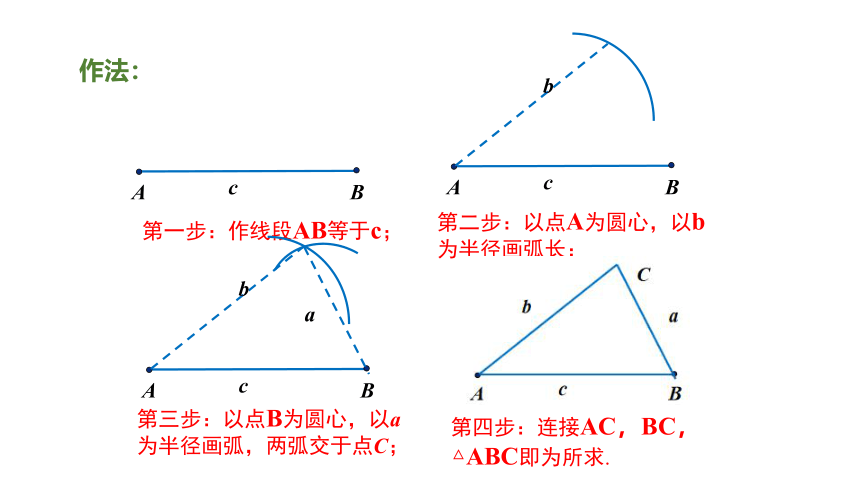
作法:
第一步:作线段AB等于c;
第二步:以点A为圆心,以b为半径画弧长;
第三步:以点B为圆心,以a为半径画弧,两弧交于点C;
第四步:连接AC,BC,△ABC即为所求.
c
B
A
c
B
A
b
c
B
A
b
a
操作:你所作的三角形与同伴所作的三角形比较,它们全等吗?为什么?
SSS:三边对应相等的两个三角形全等.
做一做 已知:两边及其夹角,线段a,c,∠α.
求作:△ABC,使BC=a,AB=c,∠ABC=∠α.(用尺规作图,保留作图痕迹,不写作法)
解析:先利用“SSS”作∠ABC=∠α,再分别截取BA=c,BC=a,从而得到△ABC,并且利用“SAS”可判断△ABC是唯一的.
操作:你所作的三角形与同伴所作的三角形比较,它们全等吗?为什么?
SAS:两边及夹角对应相等的两个三角形全等.
总结
由三角形全等判定可以知道,每一种判定两个三角形全等的条件(_____,_____,_____,_____),都只能作出唯一的三角形.
SSS
SAS
ASA
AAS
例题讲解
例2 如图,已知线段a,b,c,
求作:△ABC,使AB=a,AC=b,且BC边上中线AD=c.
温馨提示:在作较复杂的三角形时,先画草图,从中找出一个较容易作出的三角形,然后以它为基础作所求作的三角形.
作法:
(4)连接AC,△ABC即为所求.
(1)以a,b,2c为三边作△ABC,使得AB=a,BE=b,AE=2c;
(2)取AE的中点D;
(3)连接BD,并延长BD到点C,使DC=BD;
总结
复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
1.利用尺规不能唯一作出的三角形是( )
A、已知三边 B、已知两边及夹角
C、已知两角及夹边 D、已知两边及其中一边的对角
D
随堂演练
2.下列条件能作一个唯一三角形的是_________(填序号).
①∠A=65°,∠B=45°,∠C=90°;
②∠A=60°,∠B=60°,∠C=60°;
③AB=4cm,BC=3cm,AC=5cm;
④AB=2cm,BC=5cm,AC=3cm;
③
4
3.如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出 个.
解析:能画4个,分别是:
以D为圆心,AB为半径画圆;以E为圆心,AC为半径画圆.两圆相交于两点(DE上下各一个),分别于D,E连接后,可得到两个三角形.
以D为圆心,AC为半径画圆;以E为圆心,AB为半径画圆.两圆相交于两点(DE上下各一个),分别于D,E连接后,可得到两个三角形.
因此最多能画出4个.
4. 尺规作图:已知线段a,
求作:△ABC,使AB=BC=CA=a.(要求保留作图痕迹)
解析:先作AB=a,再分别以点A、B为圆心,a为半径画弧,两弧相交于点C,然后连接AC、BC即可得到△ABC.
解:如图,△ABC即为所求.
5.下面是小明设计的“已知两线段及一角作三角形”的尺规作图过程.
已知:线段m,n及∠O.
求作:△ABC,使得线段m,n及∠O分别是它的两边和一角.
作法:如图,①以点O为圆心,m长为半径画弧,
分别交∠O的两边于点M,N;
②画一条射线AP,以点A为圆心,m长为半径画弧,交AP于点B;
③以点B为圆心,MN长为半径画弧,与第②步中所画的弧相交于点D;
④画射线AD;
⑤以点A为圆心,n长为半径画弧,交AD于点C;
⑥连接BC,则△ABC即为所求作的三角形.
请回答:
(1)步骤③得到两条线段相等,即 = ;
(2)∠A=∠O的作图依据是: ;
(3)小红说小明的作图不全面,原因是: .
BD
MN
三边对应相等的两个三角形全等;全等三角形的对应角相等
小明没有对已知中的边和角的位置关系分类讨论
6.已知:△ABC,
求作:△DEF,使△DEF≌△ABC(尺规作图,保留作图痕迹).
作法:
(1)画线段EF=BC;
(2)分别以E、F为圆心,线段AB,AC为半径画弧,两弧交于点D;
(3)连接线段DE、DF.∴△DEF就是所求作的三角形.
作法不唯一,可以根据SSS来作,也可以根据SAS、ASA.
课堂小结
④已知两角和其中一角的对边作三角形
①已知三边作三角形
三角形的尺规作图
转化
②已知两边及其夹角作三角形
③已知两角及其夹边作三角形
第十三章 全等三角形
13.4 三角形的尺规作图
知识回顾
复习:1.如何用圆规和直尺作一条线段等于已知线段?
已知:线段AB.
求作:线段CD,使CD=AB.
作法:(1)画射线CE;
(2)以C为圆心,AB长为半径画弧,交CE于点D.
线段CD即为所求.
已知:∠AOB.
求作:∠A'O'B',使∠A'O'B'=∠AOB.
作法:(1)如图,以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
(2)画一条射线O'A',以点O'为圆心,OC长为半径画弧,交O'A'于点C';
(3)以点C'为圆心,CD长为半径画弧与第二步中所画的弧交于点D′;
(4)过点D'画射线O'B',则∠A'O'B'=∠AOB.
2.如何用圆规和直尺作一个角等于已知角?
问题导入
刚才回顾的用圆规和直尺作一个角等于已知角的作图中,即 ∠A'O'B'=∠AOB,为什么?
证明:在△OCD和△O'C'D'中,
∴△OCD≌△O'C'D'(SSS)
∴∠A'O'B'=∠AOB(全等三角形的对应角相等)
显然,圆规和直尺作一个角等于已知角的数学原理是全等三角形的判定,那么圆规和直尺能不能作一个已知三角形全等呢?(当然能!)这节课的任务就是三角形的尺规作图。
获取新知
尺规作图
只用直尺(没有刻度)和圆规也可以画出一些图形,这种画图方法被称为尺规作图.
知识点
概念学习:尺规作图
1
例1 下列作图属于尺规作图的是( )
A.用量角器画出∠AOB的平分线OC
B.借助直尺和圆规作∠AOB,使∠AOB=2∠α
C.画线段AB=3cm
D.用三角尺过点P作AB的垂线
B
例题讲解
解析:根据尺规作图的定义分析即可.
变式练习1 如图,用尺规作出∠OBF=∠AOB,作图痕迹 是( )
A.以点B为圆心,OD为半径的弧
B.以点B为圆心,DC为半径的弧
C.以点E为圆心,OD为半径的弧
D.以点E为圆心,DC为半径的弧
D
例1 如图,已知线段a,b,c.
求作:△ABC,使AB=c,BC=a,AC=b.
解析:由作一条线段等于已知线段,能够作出边AB,即A,B两点确定,而BC=a,AC=b,故以点A为圆心,b为半径画弧长,以点B为圆心,a为半径画弧,两弧的交点就是点C.
例题讲解
知识点
用尺规作三角形
2
作法:
第一步:作线段AB等于c;
第二步:以点A为圆心,以b为半径画弧长;
第三步:以点B为圆心,以a为半径画弧,两弧交于点C;
第四步:连接AC,BC,△ABC即为所求.
c
B
A
c
B
A
b
c
B
A
b
a
操作:你所作的三角形与同伴所作的三角形比较,它们全等吗?为什么?
SSS:三边对应相等的两个三角形全等.
做一做 已知:两边及其夹角,线段a,c,∠α.
求作:△ABC,使BC=a,AB=c,∠ABC=∠α.(用尺规作图,保留作图痕迹,不写作法)
解析:先利用“SSS”作∠ABC=∠α,再分别截取BA=c,BC=a,从而得到△ABC,并且利用“SAS”可判断△ABC是唯一的.
操作:你所作的三角形与同伴所作的三角形比较,它们全等吗?为什么?
SAS:两边及夹角对应相等的两个三角形全等.
总结
由三角形全等判定可以知道,每一种判定两个三角形全等的条件(_____,_____,_____,_____),都只能作出唯一的三角形.
SSS
SAS
ASA
AAS
例题讲解
例2 如图,已知线段a,b,c,
求作:△ABC,使AB=a,AC=b,且BC边上中线AD=c.
温馨提示:在作较复杂的三角形时,先画草图,从中找出一个较容易作出的三角形,然后以它为基础作所求作的三角形.
作法:
(4)连接AC,△ABC即为所求.
(1)以a,b,2c为三边作△ABC,使得AB=a,BE=b,AE=2c;
(2)取AE的中点D;
(3)连接BD,并延长BD到点C,使DC=BD;
总结
复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
1.利用尺规不能唯一作出的三角形是( )
A、已知三边 B、已知两边及夹角
C、已知两角及夹边 D、已知两边及其中一边的对角
D
随堂演练
2.下列条件能作一个唯一三角形的是_________(填序号).
①∠A=65°,∠B=45°,∠C=90°;
②∠A=60°,∠B=60°,∠C=60°;
③AB=4cm,BC=3cm,AC=5cm;
④AB=2cm,BC=5cm,AC=3cm;
③
4
3.如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出 个.
解析:能画4个,分别是:
以D为圆心,AB为半径画圆;以E为圆心,AC为半径画圆.两圆相交于两点(DE上下各一个),分别于D,E连接后,可得到两个三角形.
以D为圆心,AC为半径画圆;以E为圆心,AB为半径画圆.两圆相交于两点(DE上下各一个),分别于D,E连接后,可得到两个三角形.
因此最多能画出4个.
4. 尺规作图:已知线段a,
求作:△ABC,使AB=BC=CA=a.(要求保留作图痕迹)
解析:先作AB=a,再分别以点A、B为圆心,a为半径画弧,两弧相交于点C,然后连接AC、BC即可得到△ABC.
解:如图,△ABC即为所求.
5.下面是小明设计的“已知两线段及一角作三角形”的尺规作图过程.
已知:线段m,n及∠O.
求作:△ABC,使得线段m,n及∠O分别是它的两边和一角.
作法:如图,①以点O为圆心,m长为半径画弧,
分别交∠O的两边于点M,N;
②画一条射线AP,以点A为圆心,m长为半径画弧,交AP于点B;
③以点B为圆心,MN长为半径画弧,与第②步中所画的弧相交于点D;
④画射线AD;
⑤以点A为圆心,n长为半径画弧,交AD于点C;
⑥连接BC,则△ABC即为所求作的三角形.
请回答:
(1)步骤③得到两条线段相等,即 = ;
(2)∠A=∠O的作图依据是: ;
(3)小红说小明的作图不全面,原因是: .
BD
MN
三边对应相等的两个三角形全等;全等三角形的对应角相等
小明没有对已知中的边和角的位置关系分类讨论
6.已知:△ABC,
求作:△DEF,使△DEF≌△ABC(尺规作图,保留作图痕迹).
作法:
(1)画线段EF=BC;
(2)分别以E、F为圆心,线段AB,AC为半径画弧,两弧交于点D;
(3)连接线段DE、DF.∴△DEF就是所求作的三角形.
作法不唯一,可以根据SSS来作,也可以根据SAS、ASA.
课堂小结
④已知两角和其中一角的对边作三角形
①已知三边作三角形
三角形的尺规作图
转化
②已知两边及其夹角作三角形
③已知两角及其夹边作三角形
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
