第四章 几何图形初步综合提优卷(含解析)
文档属性
| 名称 | 第四章 几何图形初步综合提优卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 211.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-20 16:33:39 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
‘数学·七年级上册·RJ
第四章 综合提优卷
(考试时间90分钟,满分120分)
一、单选题(本大题共10小题,每小题3分,共30分)
1.下图中, 是正方体的展开图是( )
2.如图,点A、B在直线l上,点C是直线l外一点,可知CA+BC>AB,其依据是
A.两点之间,线段最短 B.两点确定一条直线
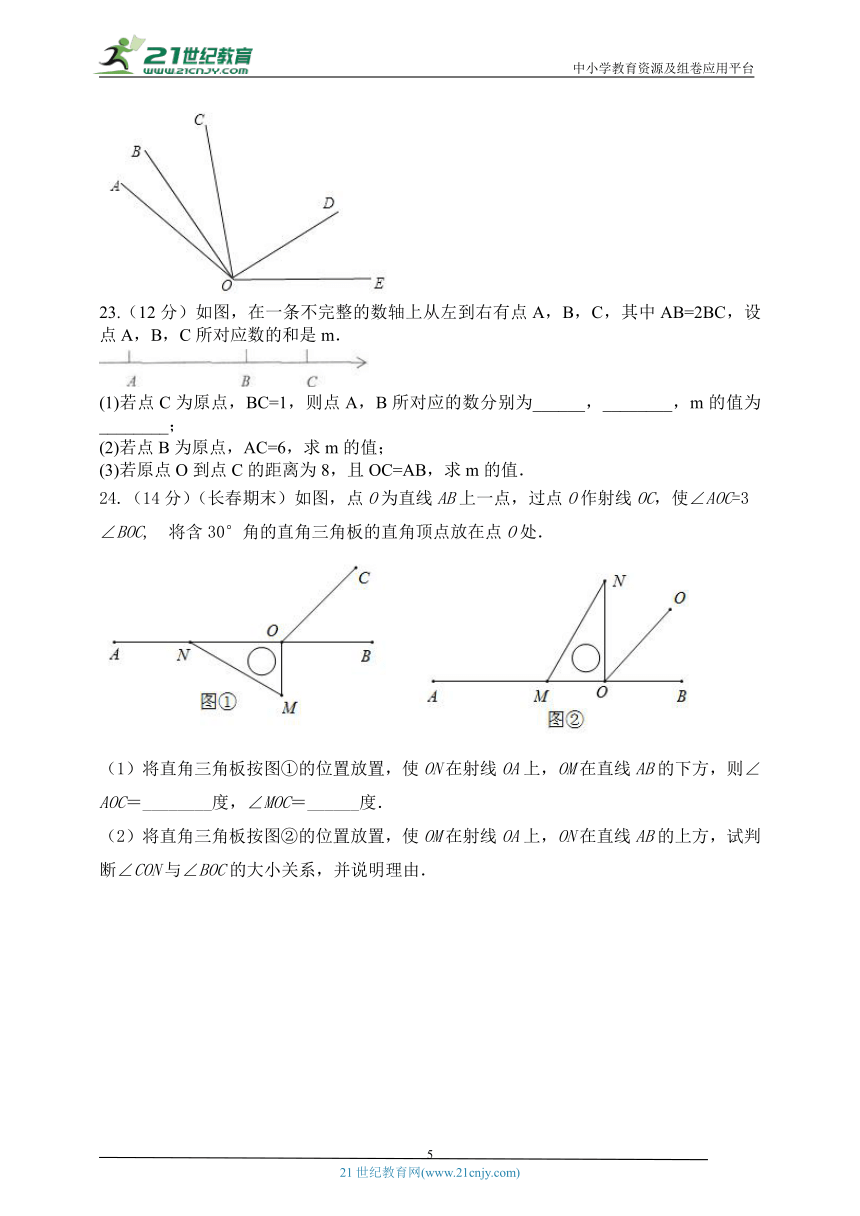
C.两点之间,直线最短 D.直线比线段长
3.若∠P=21°18′,∠Q=21.12°,∠R=21.3°,则( )
A. ∠P=∠Q B. ∠Q=∠R C. ∠P=∠R D. ∠P=∠Q=∠R
4.(成都中考)期末如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体的左面和右面所标数字相等,则x的值是( )
A. 6 B. 1 C. - D. 0
5.将选项中的四个正方体分别展开后,所得的平面展开图与如图不同的是( )
A. B. C. D.
6.(成都期末)如图,∠AOC和都∠BOD是直角,如果∠DOC=28°,那么∠AOB的度数是
A. 62° B. 152° C. 118° D. 无法确定
7已知线段AB=10cm,在直线AB上,若AC=8cm,若M,N分别为AB,AC的中点,那么M,N两点之间的距离为( )
A. 9 cm B. 1 cm C.9或1 cm D. 无法确定
8.(仁怀期末)如图用一副三角板可以画出15°的角,用它们还可以画出其它一些特殊角,不能利用这副三角板直接画出的角度是( )
A.55° B.75° C.105° D.135°
9.(东莞期末)将一副三角板按如图所示位置摆放,其中与一定互余的是
A. B.
C. D.
10.(山西太原期末)如图,∠AOB=60°,,射线OC平分∠AOB,以OC为一边作∠COP=15°,则∠BOP的度数为( )
A.15° B.45° C.15°或30° D.15°或45°
二.填空题(共8小题,每小题3分,共24分)
11.如图所示,若图中共有m条线段,n条射线,则n-m=______ .
12.如图,已知C,D两点在线段AB上,AB=10cm,CD=6cm,M,N分别是线段AC,BD的中点,则MN=________cm.
13.用棱长是的小正方体组成如图所示的几何体,把这个几何体放在桌子上,并把暴露的面涂上颜色,那么涂颜色面的面积之和是_____.
14.已知数轴上A、B两点所表示的数分别为-6和4,则AB中点表示的数是_____。
15.(哈尔滨月考)如图,OA的方向是北偏东15°,OB的方向是北偏西40°,若∠AOC=∠AOB,则OC的方向是_ _.
16.平面内,已知,,平分,平分,则 .
17.(成都武侯区月考)有一个正方体的六个面上分别标有数字1、2、3、4、5、6,从三个不同的角度观察这个正方体所得到的结果如图所示,如果标有数字6的面所对面上的数字记为a,2的面所对面上数字记为b,那么2a+3b的值为_______ .
18.(铜仁期末)在数轴上,点A表示的数是4,点B表示的数是-5,点A以每秒2个单位长度的速度向负方向移动,当A、B两点距离为1时,点A移动了 秒。
解答题(共66分)
19.(6分)(贵阳期末)如图是由9个小立方块搭成的几何体,请在下面方格纸中分别画出从正面、左面、上面看到的几何体的形状图.
20.(10分)如图所示,AB为一条直线,OC是∠AOD的平分线,OE在∠BOD内,∠DOE:∠BOD=2:5,∠COE=80°,求∠EOB的度数.
21.如图,已知点C为AB上一点,AC=12cm,CB=AC,D、E分别为AC,AB的中点,求DE的长.
22.(12分)如图,若∠AOE=150°,∠AOB:∠BOC=1:2,∠COD:∠DOE=2:1,求∠BOD的度数.
23.(12分)如图,在一条不完整的数轴上从左到右有点A,B,C,其中AB=2BC,设点A,B,C所对应数的和是m.
(1)若点C为原点,BC=1,则点A,B所对应的数分别为______,________,m的值为________;
(2)若点B为原点,AC=6,求m的值;
(3)若原点O到点C的距离为8,且OC=AB,求m的值.
24.(14分)(长春期末)如图,点O为直线AB上一点,过点O作射线OC,使∠AOC=3∠BOC, 将含30°角的直角三角板的直角顶点放在点O处.
(1)将直角三角板按图①的位置放置,使ON在射线OA上,OM在直线AB的下方,则∠AOC=________度,∠MOC=______度.
(2)将直角三角板按图②的位置放置,使OM在射线OA上,ON在直线AB的上方,试判断∠CON与∠BOC的大小关系,并说明理由.
第四章 综合提优卷
1.B 〖解析〗A、C、D均不是正方体表面展开图;
故答案为:B.
点拨:考查了几何体的展开图 ,正方体的展开图不能是凹字格、田字格
2.A 〖解析〗 根据两点之间,线段最短
故答案为:A
C 〖解析〗∵∠P=21°18′=21.3°,∠Q=21.12°=21°,∠R=21.3°
∴∠P=∠R
故选C.
点拨:本题考查了度、分、秒之间的换算,角的大小比较的应用,能理解度、分、秒之间的关系是解此题的关键.
4.C 〖解析〗:根据题意得x﹣3=3x﹣2,
解得x=﹣.
故选C.
点拨:考查了正方体及其表面展开图及特点,列出方程x﹣3=3x﹣2是关键。
5.B 〖解析〗观察图形可知,
将选项中的四个正方体分别展开后,所得的平面展开图与如图不同的选项B.
故选:B.
点拨:立体图形的侧面展开图,体现了平面图形与立体图形的联系.立体图形问题可以转化为平面图形问题解决.
6.B 〖解析〗 ∵∠AOC=90°,∠DOC=28°
∴∠AOD=90°-28°=62°
∴∠AOB=∠BOD+∠AOD=90°+62°=152°
故选:B
点拨:考查了角的和差,找到角的和差关系是关键。
C 〖解析〗(1)∵M为AB的中点,
∴MB=AB=5cm,
∵N为AC的中点,
∴NA=NC=4cm,
∴MN=MA-NA=1cm;
(2)∵M为AB的中点,
∴MB=AB=5cm,
∵N为BC的中点,
∴∵N为AC的中点,
∴NA=NC=4cm,,
∴MN=MA+AN=9cm.
故选C
点拨: 此类试题属于难度一般的试题,但是考生在解答此类试题时一定要学会区分情况去作答。
8.A 〖解析〗(1)55°不可以;
(2)45°+30°=75°可以;
(3)60°+45°=105°可以;
(4)90°+45°=135°可以;
故选A.
点拨:本题是数学上常见的知识,要记牢固.
9 .B 〖解析〗A.∠α与∠β相等,∠α与不∠β一定互余,故本选项错误;
B. ∠α+ ∠β=180°-90°=90°,正确;
C.∠α与∠β不互余,∠α与∠β互补,故本选项错误;
D.∠α与∠β不互余,故本选项错误.
故选B
点拨:本题考查了余角与补角和识图能力。
D 〖解析〗:当射线OP位于射线OA与OC之间时,
∠BOP=∠BOC+∠COP=30°+15°=45°
当射线OP位于射线OB与OC之间时,
∠BOP=∠BOC-∠COP=30°-15°=15°
故选D
点拨:本题用了分类讨论思想.画出正确的图形是解题的关键。
二、填空题
11. 6 〖解析〗 ∵n=16,m=10
∴n-m=16-10=6
故答案是:6
12.8 〖解析〗∵M、N分别是AC、BD的中点,
∴MC=AC, DN=DB
∴MC+DN=AC+DB
=(AC+BD)
=(AB-CD)
=(10-6)=2
∴MN=MC+DN+CD=2+6=8
故答案为:8.
点拨:本题考查了中点的定义及两点之间的距离的求法,准确识图是解题的关键.
13.30cm 〖解析〗 主视图中正方形有6个;
左视图中正方形有6个;
俯视图中正方形有6个.
则这个几何体中正方形的个数是:6×2+6×2+6×1=30个
故答案为:30cm2.
14.-1 〖解析〗数轴上两点的中点=(x1+x2)=(-6+4)=-1
15.70° 〖解析〗∵OA的方向是北偏东15°,OB的方向是北偏西40°
∴∠AOB=40°+15°=55°
∵∠AOC=∠AOB
∴OC的方向是北偏东15°+55°=70°.
故答案为:70°
16.35°或55° 〖解析〗 当OC在∠AOB内时,如图1,
;
当OC在外∠AOB时,如图2,
,
故答案为:35°或55°.
点拨:本题主要考查了角的和差,角平分线的定义,关键是分情况讨论.
17.18 〖解析〗从3个小立方体上的数可知,
与写有数字1的面相邻的面上数字是2,3,4,6,
所以数字1面对数字5,
同理,立方体面上数字3对6.
故立方体面上数字2对4.
则a=6,b=2,
那么2a+3b=18.
故答案为:18
点拨:本题考查的知识点是棱柱的结构特征,其中根据已知中的三个图形,分析出相对两面的三组数字,是解答本题的关键.
18. 4或5秒 〖解析〗 A表示的数是4,B表示的数是-5,
又因为A、B之间的距离为1,
所以A运动到-4或-6
当A运动到-4时,A 走过的路程为4-(-4)=8
所以A运动的时间为8÷2=4秒
当A运动到-6时,A 走过的路程为4-(-6)=10
所以A运动的时间为10÷2=5秒
故答案为:4或5秒
19.解:
20.解:如图,设∠DOE=2x
又因为∠DOE:∠BOD=2:5
则∠EOB=3x
又因为OC是∠AOD的平分线,∠COE=80°
所以∠AOC=∠COD=80°-2x
2×(80°-2x)+5x=180°
解得x=20°
所以∠BOE=3x=3×20°=60°
21.解:因为AC=12cm,CB=AC
所以CB=6cm
所以AB=AC+BC=12+6=18cm
因为D为AC的中点
所以DC=AD=6cm
因为E为AB的中点
所以AE=BE=9cm
所以DE=AE-AD=3cm
22.解:因为∠AOB:∠BOC=1:2,∠COD:∠DOE=2:1,
所以设∠AOB=x°,∠DOE=y°,则∠BOC=(2x)°,∠COD=(2y)°,
所以∠AOB+∠DOE=x°+y°,因为∠AOE=150°,
所以3x°+3y°=150°,
所以x°+y°=50°,
所以∠BOD=2x°+2y°,
=2×(x°+y°),
=2×50°,
=100°.
23.解:(1)-3,-1;-4;
(2)若以B为原点,AC=6,AB=2BC,
则AB=4,BC=2,
则点A所对应的数为-4,点B对应的数为0,点C对应的数为2,
此时m=-4+2+0=-2;
(3)根据题意知,
①当点O在点C的左侧时,
设BC=x,则OC=AB=2BC=2x,AO=OB=BC=x,
所以OC=8,
所以2x=8,
所以x=4,
所以点A、B、C对应的数为-4、4、8;
m的值为-4+4+8=8;
②当点O在点C的右侧时,
设BC=x,则OC=AB=2BC=2x,OA=5x,OB=3x,
所以OC=8
所以2x=8
所以x=4
所以点A、B、C对应的数为-20、-12、-8;
m的值为-20-12-8=-40.
综上,m的值为8或-40.
24.解:(1)因为∠AOC=3∠BOC,
所以∠AOC=×180°=135°,
所以∠BOC=×180°=45°,
所以∠MOC=∠BOM+∠BOC=90°+45°=135°.
故答案是:135,135;
(2)∠CON=∠BOC .
由(1)知,∠AOC=135°,∠BOC=45°,
因为∠CON=∠AOC-∠MON,
所以 ∠CON=135°-45°=45°,
所以∠CON=∠BOC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
‘数学·七年级上册·RJ
第四章 综合提优卷
(考试时间90分钟,满分120分)
一、单选题(本大题共10小题,每小题3分,共30分)
1.下图中, 是正方体的展开图是( )
2.如图,点A、B在直线l上,点C是直线l外一点,可知CA+BC>AB,其依据是
A.两点之间,线段最短 B.两点确定一条直线
C.两点之间,直线最短 D.直线比线段长
3.若∠P=21°18′,∠Q=21.12°,∠R=21.3°,则( )
A. ∠P=∠Q B. ∠Q=∠R C. ∠P=∠R D. ∠P=∠Q=∠R
4.(成都中考)期末如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体的左面和右面所标数字相等,则x的值是( )
A. 6 B. 1 C. - D. 0
5.将选项中的四个正方体分别展开后,所得的平面展开图与如图不同的是( )
A. B. C. D.
6.(成都期末)如图,∠AOC和都∠BOD是直角,如果∠DOC=28°,那么∠AOB的度数是
A. 62° B. 152° C. 118° D. 无法确定
7已知线段AB=10cm,在直线AB上,若AC=8cm,若M,N分别为AB,AC的中点,那么M,N两点之间的距离为( )
A. 9 cm B. 1 cm C.9或1 cm D. 无法确定
8.(仁怀期末)如图用一副三角板可以画出15°的角,用它们还可以画出其它一些特殊角,不能利用这副三角板直接画出的角度是( )
A.55° B.75° C.105° D.135°
9.(东莞期末)将一副三角板按如图所示位置摆放,其中与一定互余的是
A. B.
C. D.
10.(山西太原期末)如图,∠AOB=60°,,射线OC平分∠AOB,以OC为一边作∠COP=15°,则∠BOP的度数为( )
A.15° B.45° C.15°或30° D.15°或45°
二.填空题(共8小题,每小题3分,共24分)
11.如图所示,若图中共有m条线段,n条射线,则n-m=______ .
12.如图,已知C,D两点在线段AB上,AB=10cm,CD=6cm,M,N分别是线段AC,BD的中点,则MN=________cm.
13.用棱长是的小正方体组成如图所示的几何体,把这个几何体放在桌子上,并把暴露的面涂上颜色,那么涂颜色面的面积之和是_____.
14.已知数轴上A、B两点所表示的数分别为-6和4,则AB中点表示的数是_____。
15.(哈尔滨月考)如图,OA的方向是北偏东15°,OB的方向是北偏西40°,若∠AOC=∠AOB,则OC的方向是_ _.
16.平面内,已知,,平分,平分,则 .
17.(成都武侯区月考)有一个正方体的六个面上分别标有数字1、2、3、4、5、6,从三个不同的角度观察这个正方体所得到的结果如图所示,如果标有数字6的面所对面上的数字记为a,2的面所对面上数字记为b,那么2a+3b的值为_______ .
18.(铜仁期末)在数轴上,点A表示的数是4,点B表示的数是-5,点A以每秒2个单位长度的速度向负方向移动,当A、B两点距离为1时,点A移动了 秒。
解答题(共66分)
19.(6分)(贵阳期末)如图是由9个小立方块搭成的几何体,请在下面方格纸中分别画出从正面、左面、上面看到的几何体的形状图.
20.(10分)如图所示,AB为一条直线,OC是∠AOD的平分线,OE在∠BOD内,∠DOE:∠BOD=2:5,∠COE=80°,求∠EOB的度数.
21.如图,已知点C为AB上一点,AC=12cm,CB=AC,D、E分别为AC,AB的中点,求DE的长.
22.(12分)如图,若∠AOE=150°,∠AOB:∠BOC=1:2,∠COD:∠DOE=2:1,求∠BOD的度数.
23.(12分)如图,在一条不完整的数轴上从左到右有点A,B,C,其中AB=2BC,设点A,B,C所对应数的和是m.
(1)若点C为原点,BC=1,则点A,B所对应的数分别为______,________,m的值为________;
(2)若点B为原点,AC=6,求m的值;
(3)若原点O到点C的距离为8,且OC=AB,求m的值.
24.(14分)(长春期末)如图,点O为直线AB上一点,过点O作射线OC,使∠AOC=3∠BOC, 将含30°角的直角三角板的直角顶点放在点O处.
(1)将直角三角板按图①的位置放置,使ON在射线OA上,OM在直线AB的下方,则∠AOC=________度,∠MOC=______度.
(2)将直角三角板按图②的位置放置,使OM在射线OA上,ON在直线AB的上方,试判断∠CON与∠BOC的大小关系,并说明理由.
第四章 综合提优卷
1.B 〖解析〗A、C、D均不是正方体表面展开图;
故答案为:B.
点拨:考查了几何体的展开图 ,正方体的展开图不能是凹字格、田字格
2.A 〖解析〗 根据两点之间,线段最短
故答案为:A
C 〖解析〗∵∠P=21°18′=21.3°,∠Q=21.12°=21°,∠R=21.3°
∴∠P=∠R
故选C.
点拨:本题考查了度、分、秒之间的换算,角的大小比较的应用,能理解度、分、秒之间的关系是解此题的关键.
4.C 〖解析〗:根据题意得x﹣3=3x﹣2,
解得x=﹣.
故选C.
点拨:考查了正方体及其表面展开图及特点,列出方程x﹣3=3x﹣2是关键。
5.B 〖解析〗观察图形可知,
将选项中的四个正方体分别展开后,所得的平面展开图与如图不同的选项B.
故选:B.
点拨:立体图形的侧面展开图,体现了平面图形与立体图形的联系.立体图形问题可以转化为平面图形问题解决.
6.B 〖解析〗 ∵∠AOC=90°,∠DOC=28°
∴∠AOD=90°-28°=62°
∴∠AOB=∠BOD+∠AOD=90°+62°=152°
故选:B
点拨:考查了角的和差,找到角的和差关系是关键。
C 〖解析〗(1)∵M为AB的中点,
∴MB=AB=5cm,
∵N为AC的中点,
∴NA=NC=4cm,
∴MN=MA-NA=1cm;
(2)∵M为AB的中点,
∴MB=AB=5cm,
∵N为BC的中点,
∴∵N为AC的中点,
∴NA=NC=4cm,,
∴MN=MA+AN=9cm.
故选C
点拨: 此类试题属于难度一般的试题,但是考生在解答此类试题时一定要学会区分情况去作答。
8.A 〖解析〗(1)55°不可以;
(2)45°+30°=75°可以;
(3)60°+45°=105°可以;
(4)90°+45°=135°可以;
故选A.
点拨:本题是数学上常见的知识,要记牢固.
9 .B 〖解析〗A.∠α与∠β相等,∠α与不∠β一定互余,故本选项错误;
B. ∠α+ ∠β=180°-90°=90°,正确;
C.∠α与∠β不互余,∠α与∠β互补,故本选项错误;
D.∠α与∠β不互余,故本选项错误.
故选B
点拨:本题考查了余角与补角和识图能力。
D 〖解析〗:当射线OP位于射线OA与OC之间时,
∠BOP=∠BOC+∠COP=30°+15°=45°
当射线OP位于射线OB与OC之间时,
∠BOP=∠BOC-∠COP=30°-15°=15°
故选D
点拨:本题用了分类讨论思想.画出正确的图形是解题的关键。
二、填空题
11. 6 〖解析〗 ∵n=16,m=10
∴n-m=16-10=6
故答案是:6
12.8 〖解析〗∵M、N分别是AC、BD的中点,
∴MC=AC, DN=DB
∴MC+DN=AC+DB
=(AC+BD)
=(AB-CD)
=(10-6)=2
∴MN=MC+DN+CD=2+6=8
故答案为:8.
点拨:本题考查了中点的定义及两点之间的距离的求法,准确识图是解题的关键.
13.30cm 〖解析〗 主视图中正方形有6个;
左视图中正方形有6个;
俯视图中正方形有6个.
则这个几何体中正方形的个数是:6×2+6×2+6×1=30个
故答案为:30cm2.
14.-1 〖解析〗数轴上两点的中点=(x1+x2)=(-6+4)=-1
15.70° 〖解析〗∵OA的方向是北偏东15°,OB的方向是北偏西40°
∴∠AOB=40°+15°=55°
∵∠AOC=∠AOB
∴OC的方向是北偏东15°+55°=70°.
故答案为:70°
16.35°或55° 〖解析〗 当OC在∠AOB内时,如图1,
;
当OC在外∠AOB时,如图2,
,
故答案为:35°或55°.
点拨:本题主要考查了角的和差,角平分线的定义,关键是分情况讨论.
17.18 〖解析〗从3个小立方体上的数可知,
与写有数字1的面相邻的面上数字是2,3,4,6,
所以数字1面对数字5,
同理,立方体面上数字3对6.
故立方体面上数字2对4.
则a=6,b=2,
那么2a+3b=18.
故答案为:18
点拨:本题考查的知识点是棱柱的结构特征,其中根据已知中的三个图形,分析出相对两面的三组数字,是解答本题的关键.
18. 4或5秒 〖解析〗 A表示的数是4,B表示的数是-5,
又因为A、B之间的距离为1,
所以A运动到-4或-6
当A运动到-4时,A 走过的路程为4-(-4)=8
所以A运动的时间为8÷2=4秒
当A运动到-6时,A 走过的路程为4-(-6)=10
所以A运动的时间为10÷2=5秒
故答案为:4或5秒
19.解:
20.解:如图,设∠DOE=2x
又因为∠DOE:∠BOD=2:5
则∠EOB=3x
又因为OC是∠AOD的平分线,∠COE=80°
所以∠AOC=∠COD=80°-2x
2×(80°-2x)+5x=180°
解得x=20°
所以∠BOE=3x=3×20°=60°
21.解:因为AC=12cm,CB=AC
所以CB=6cm
所以AB=AC+BC=12+6=18cm
因为D为AC的中点
所以DC=AD=6cm
因为E为AB的中点
所以AE=BE=9cm
所以DE=AE-AD=3cm
22.解:因为∠AOB:∠BOC=1:2,∠COD:∠DOE=2:1,
所以设∠AOB=x°,∠DOE=y°,则∠BOC=(2x)°,∠COD=(2y)°,
所以∠AOB+∠DOE=x°+y°,因为∠AOE=150°,
所以3x°+3y°=150°,
所以x°+y°=50°,
所以∠BOD=2x°+2y°,
=2×(x°+y°),
=2×50°,
=100°.
23.解:(1)-3,-1;-4;
(2)若以B为原点,AC=6,AB=2BC,
则AB=4,BC=2,
则点A所对应的数为-4,点B对应的数为0,点C对应的数为2,
此时m=-4+2+0=-2;
(3)根据题意知,
①当点O在点C的左侧时,
设BC=x,则OC=AB=2BC=2x,AO=OB=BC=x,
所以OC=8,
所以2x=8,
所以x=4,
所以点A、B、C对应的数为-4、4、8;
m的值为-4+4+8=8;
②当点O在点C的右侧时,
设BC=x,则OC=AB=2BC=2x,OA=5x,OB=3x,
所以OC=8
所以2x=8
所以x=4
所以点A、B、C对应的数为-20、-12、-8;
m的值为-20-12-8=-40.
综上,m的值为8或-40.
24.解:(1)因为∠AOC=3∠BOC,
所以∠AOC=×180°=135°,
所以∠BOC=×180°=45°,
所以∠MOC=∠BOM+∠BOC=90°+45°=135°.
故答案是:135,135;
(2)∠CON=∠BOC .
由(1)知,∠AOC=135°,∠BOC=45°,
因为∠CON=∠AOC-∠MON,
所以 ∠CON=135°-45°=45°,
所以∠CON=∠BOC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
