人教A版(2019)选择性必修第一册2.1.2 两条直线平行和垂直的判定 课件(共16张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册2.1.2 两条直线平行和垂直的判定 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 307.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-21 08:41:27 | ||
图片预览



文档简介
(共16张PPT)
2.1.2 两条直线平行和垂直的判定
为了表示直线的倾斜程度,我们引入了直线倾斜角与斜率的概念,并导出了计算斜率的公式,即把几何问题转化为代数问题。
那么,我们能否通过直线l1、l2的斜率k1、k2来判断两条直线的位置关系呢?
我们约定:若没有特别说明,说“两条直线l1与l2”时,一般是指两条不重合的直线。
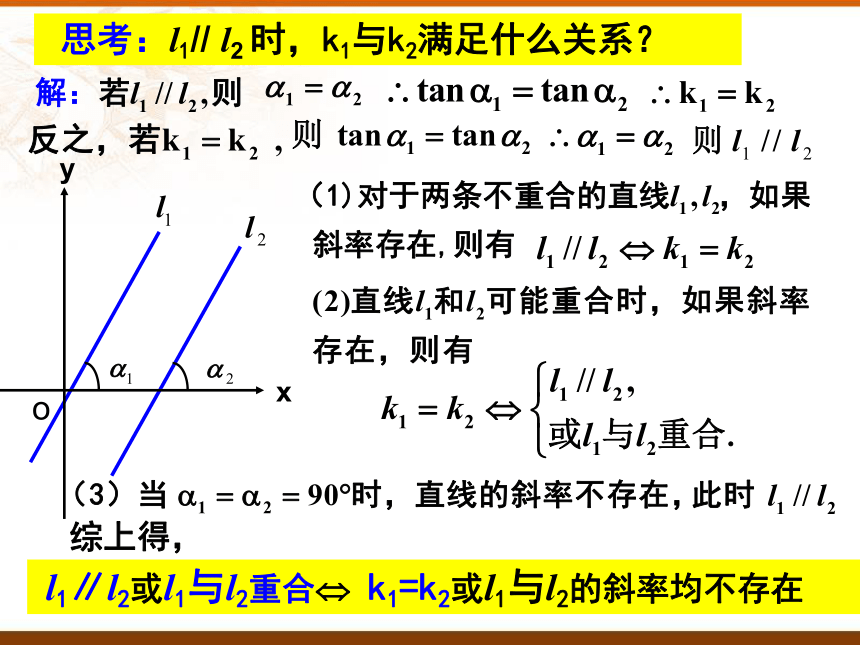
思考:l1// l2 时,k1与k2满足什么关系?
o
y
x
l1∥l2或l1与l2重合 k1=k2或l1与l2的斜率均不存在
综上得,
如果直线l1,l2的斜率为k1,k2. 那么:
*若两直线倾斜角都为90°,则两直线互相平行.
l1∥l2或l1与l2重合 k1=k2或l1与l2的斜率均不存在
综上得:
2.两直线的斜率都不存在时:
1.两直线不重合且斜率都存在时:
l1∥l2 k1=k2
一、两直线平行的判定
(用斜率证明三点共线时,常用这个结论)
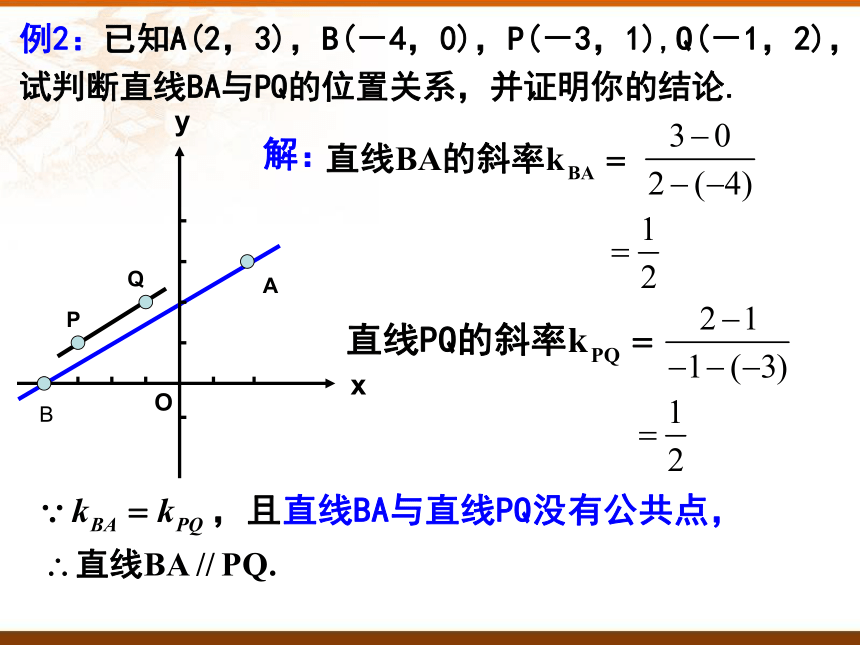
例2:已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线BA与PQ的位置关系,并证明你的结论.
x
y
O
B
A
P
Q
解:
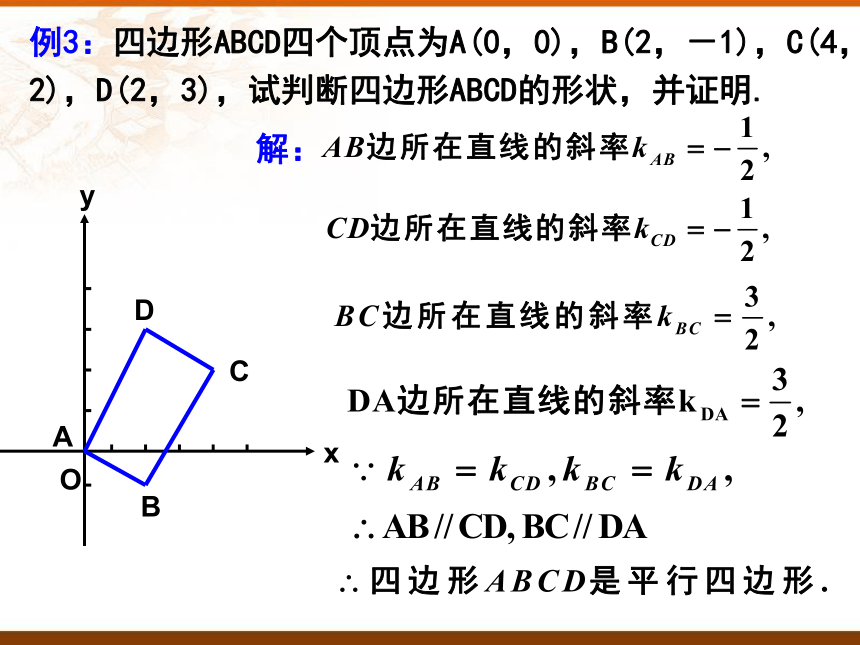
例3:四边形ABCD四个顶点为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并证明.
解:
x
y
O
A
B
C
D
解:
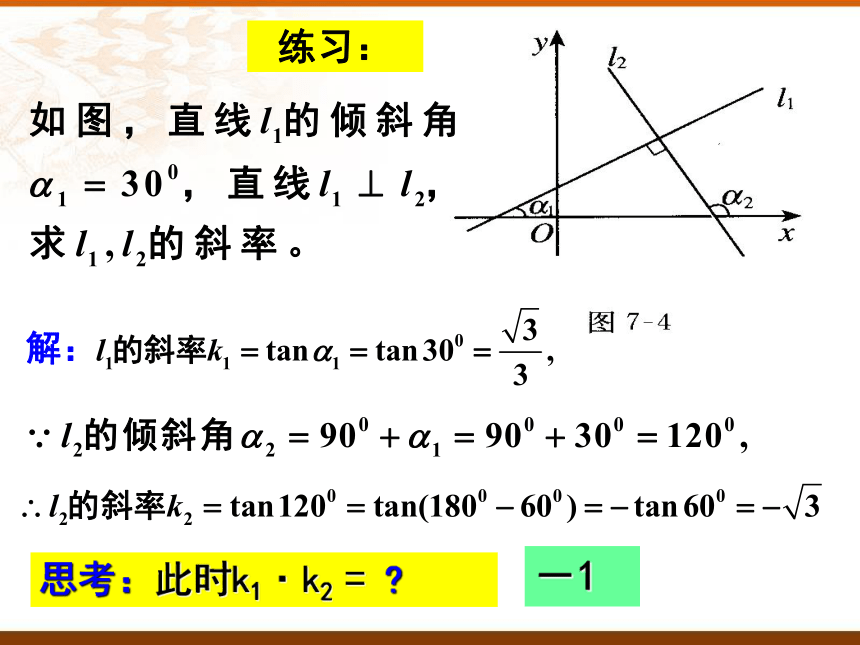
练习:
思考:此时k1·k2 =
-1
思考:当l1⊥l2时,它们的斜率除了不相等外,是否还有特殊的数量关系?
二、两直线垂直的判定
思考:当l1⊥l2时,它们的斜率除了不相等外,是否还有特殊的数量关系?
2.特殊情况下的两直线垂直:
若一条直线没有斜率,另一条直线的斜率为0,则两条直线互相垂直
综上得,
如果直线l1,l2的斜率为k1,k2 ,那么
1.两直线斜率都存在时:
二、两直线垂直的判定
例4:已知A(-6,0),B(3,6),P(0,3),Q(6,-6),试判断直线AB与PQ的位置关系.
解:
例题讲解:
例5:已知A(5,-1),B(1,1),C(2,3)三点,试判断三角形ABC的形状.
解:
x
y
O
A
B
C
例题讲解:
如果直线l1,l2的斜率为k1,k2. 那么:
*若两直线倾斜角都为90°,则两直线互相平行.
l1∥l2或l1与l2重合 k1=k2或l1与l2的斜率均不存在
综上得:
2.两直线的斜率都不存在时:
1.两直线不重合且斜率都存在时:
l1∥l2 k1=k2
(用斜率证明三点共线时,常用这个结论)
(一)两直线平行的判定
三、归纳小结
2.特殊情况下的两直线垂直:
若一条直线没有斜率,另一条直线的斜率为0,则两条直线互相垂直
综上得,
如果直线l1,l2的斜率为k1,k2 ,那么
1.两直线斜率都存在时:
(二)两直线垂直的判定
三、归纳小结:
请看课本P57:习题2.1 第3,7,8,9题
1、判断下列各对直线平行还是垂直:
(1)经过两点A(2,3),B(-1,0)的直线l1,与经过点P(1,0)且斜率为1的直线l2;
(2)经过两点C(3,1),D(- 2,0)的直线l3,与经过点M(1,-4)且斜率为-5的直线l4 。
2、试确定m的值,使过点A(m,1),B(-1,m)的直线与过点P(1,2),Q(-5,0)的直线:
(1)平行;
(2)垂直。
平行
垂直
m =-2
请看课本P57:练习
1.直线l1,l2的斜率k1,k2是关于k的方程 2k2-3k-b=0的两根,若l1⊥l2,则b=_____;若l1∥l2,则b=_______
学以致用:
2.直线l 的倾斜角为30°,点P(2,1)在直线l上,直线l 绕点P(2,1)按逆时针方向旋转30°后到达直线l1的位置,且直线l1与l2平行,l2是线段AB的垂直平分线,A(1,m-1),B(m,2),试求m的值.
2
2.1.2 两条直线平行和垂直的判定
为了表示直线的倾斜程度,我们引入了直线倾斜角与斜率的概念,并导出了计算斜率的公式,即把几何问题转化为代数问题。
那么,我们能否通过直线l1、l2的斜率k1、k2来判断两条直线的位置关系呢?
我们约定:若没有特别说明,说“两条直线l1与l2”时,一般是指两条不重合的直线。
思考:l1// l2 时,k1与k2满足什么关系?
o
y
x
l1∥l2或l1与l2重合 k1=k2或l1与l2的斜率均不存在
综上得,
如果直线l1,l2的斜率为k1,k2. 那么:
*若两直线倾斜角都为90°,则两直线互相平行.
l1∥l2或l1与l2重合 k1=k2或l1与l2的斜率均不存在
综上得:
2.两直线的斜率都不存在时:
1.两直线不重合且斜率都存在时:
l1∥l2 k1=k2
一、两直线平行的判定
(用斜率证明三点共线时,常用这个结论)
例2:已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线BA与PQ的位置关系,并证明你的结论.
x
y
O
B
A
P
Q
解:
例3:四边形ABCD四个顶点为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并证明.
解:
x
y
O
A
B
C
D
解:
练习:
思考:此时k1·k2 =
-1
思考:当l1⊥l2时,它们的斜率除了不相等外,是否还有特殊的数量关系?
二、两直线垂直的判定
思考:当l1⊥l2时,它们的斜率除了不相等外,是否还有特殊的数量关系?
2.特殊情况下的两直线垂直:
若一条直线没有斜率,另一条直线的斜率为0,则两条直线互相垂直
综上得,
如果直线l1,l2的斜率为k1,k2 ,那么
1.两直线斜率都存在时:
二、两直线垂直的判定
例4:已知A(-6,0),B(3,6),P(0,3),Q(6,-6),试判断直线AB与PQ的位置关系.
解:
例题讲解:
例5:已知A(5,-1),B(1,1),C(2,3)三点,试判断三角形ABC的形状.
解:
x
y
O
A
B
C
例题讲解:
如果直线l1,l2的斜率为k1,k2. 那么:
*若两直线倾斜角都为90°,则两直线互相平行.
l1∥l2或l1与l2重合 k1=k2或l1与l2的斜率均不存在
综上得:
2.两直线的斜率都不存在时:
1.两直线不重合且斜率都存在时:
l1∥l2 k1=k2
(用斜率证明三点共线时,常用这个结论)
(一)两直线平行的判定
三、归纳小结
2.特殊情况下的两直线垂直:
若一条直线没有斜率,另一条直线的斜率为0,则两条直线互相垂直
综上得,
如果直线l1,l2的斜率为k1,k2 ,那么
1.两直线斜率都存在时:
(二)两直线垂直的判定
三、归纳小结:
请看课本P57:习题2.1 第3,7,8,9题
1、判断下列各对直线平行还是垂直:
(1)经过两点A(2,3),B(-1,0)的直线l1,与经过点P(1,0)且斜率为1的直线l2;
(2)经过两点C(3,1),D(- 2,0)的直线l3,与经过点M(1,-4)且斜率为-5的直线l4 。
2、试确定m的值,使过点A(m,1),B(-1,m)的直线与过点P(1,2),Q(-5,0)的直线:
(1)平行;
(2)垂直。
平行
垂直
m =-2
请看课本P57:练习
1.直线l1,l2的斜率k1,k2是关于k的方程 2k2-3k-b=0的两根,若l1⊥l2,则b=_____;若l1∥l2,则b=_______
学以致用:
2.直线l 的倾斜角为30°,点P(2,1)在直线l上,直线l 绕点P(2,1)按逆时针方向旋转30°后到达直线l1的位置,且直线l1与l2平行,l2是线段AB的垂直平分线,A(1,m-1),B(m,2),试求m的值.
2
