数学人教A版(2019)选择性必修第一册2.2.1 直线的点斜式方程(共25张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.2.1 直线的点斜式方程(共25张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 573.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-21 18:29:34 | ||
图片预览



文档简介
(共25张PPT)
如果直线l1,l2的斜率为k1,k2. 那么:
*若两直线倾斜角都为90°,则两直线互相平行.
l1∥l2或l1与l2重合 k1=k2或l1与l2的斜率均不存在
综上得:
2.两直线的斜率都不存在时:
1.两直线不重合且斜率都存在时:
l1∥l2 k1=k2
(用斜率证明三点共线时,常用这个结论)
(一)两直线平行的判定
温故而知新
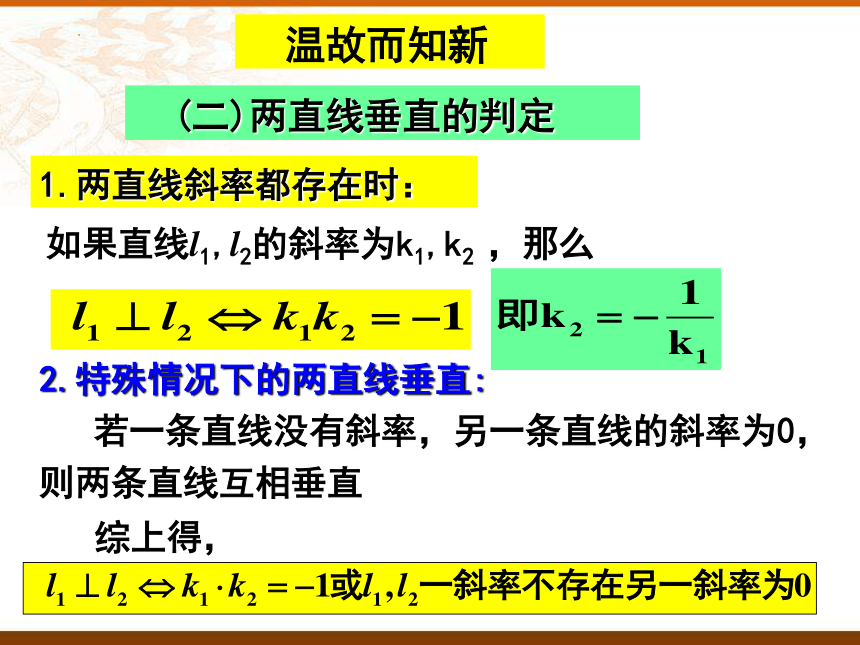
2.特殊情况下的两直线垂直:
若一条直线没有斜率,另一条直线的斜率为0,则两条直线互相垂直
综上得,
如果直线l1,l2的斜率为k1,k2 ,那么
1.两直线斜率都存在时:
(二)两直线垂直的判定
温故而知新
2.2.1 直线的点斜式方程
1.如何确定一条直线?
答:(1)已知两点可以确定一条直线。
(2)已知直线上的一点和直线的倾斜角(斜率)可以确定一条直线。
复习引入:
4.斜率公式:
3.直线的斜率定义:
2.直线的倾斜角定义及其范围:
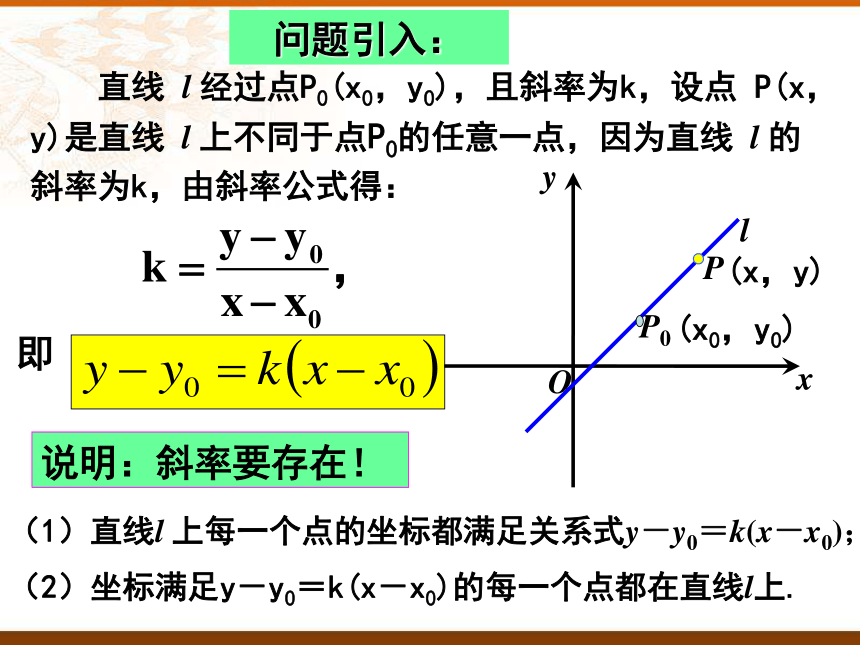
直线 l 经过点P0(x0,y0),且斜率为k,设点 P(x,y)是直线 l 上不同于点P0的任意一点,因为直线 l 的斜率为k,由斜率公式得:
即
x
y
O
l
P0
P
问题引入:
(1)直线l 上每一个点的坐标都满足关系式y-y0=k(x-x0);
(2)坐标满足y-y0=k(x-x0)的每一个点都在直线l上.
说明:斜率要存在!
(x0,y0)
(x,y)
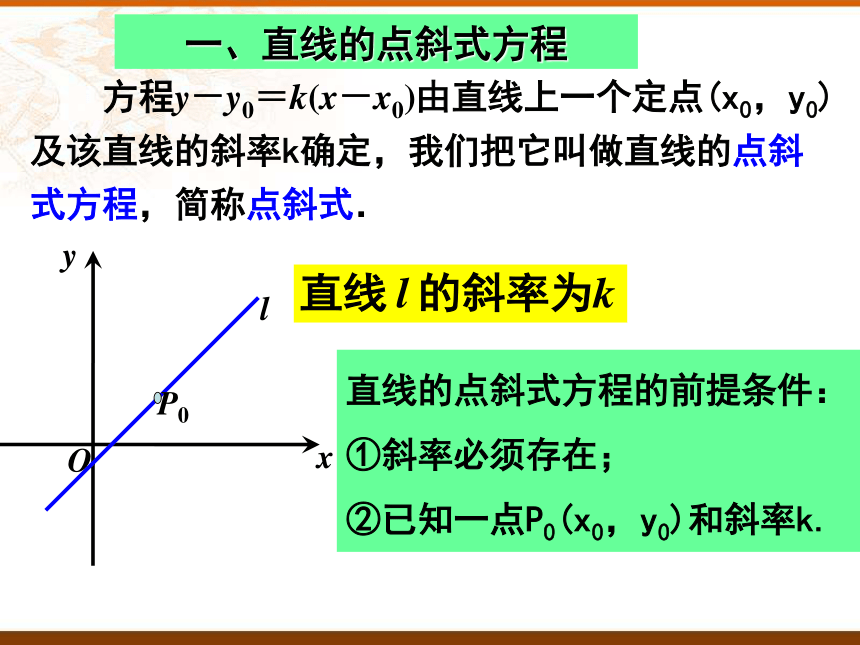
方程y-y0=k(x-x0)由直线上一个定点(x0,y0)及该直线的斜率k确定,我们把它叫做直线的点斜式方程,简称点斜式.
一、直线的点斜式方程
x
y
O
l
P0
直线的点斜式方程的前提条件:
①斜率必须存在;
②已知一点P0(x0,y0)和斜率k.
x
y
l
P0(x0 , y0)
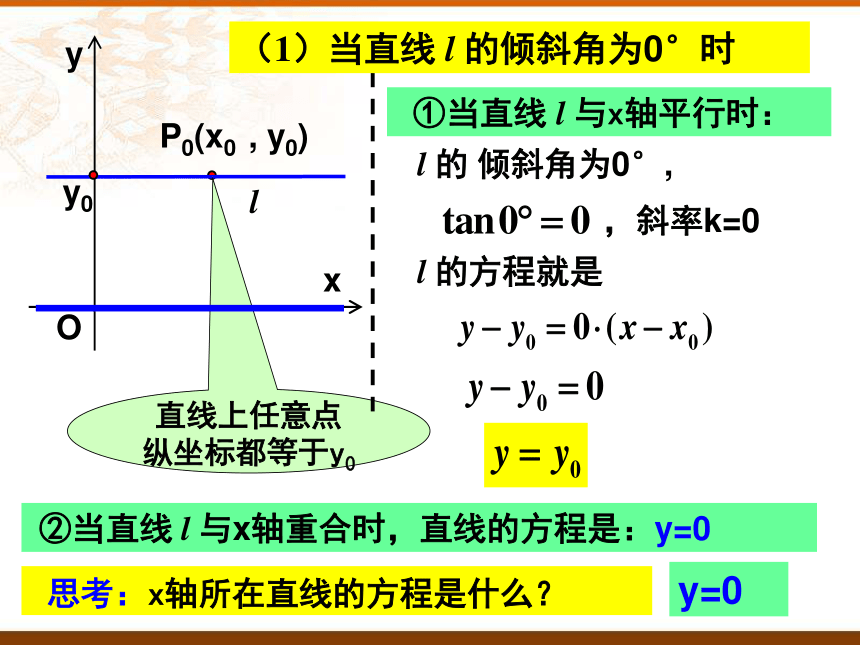
l 的 倾斜角为0°,
,斜率k=0
y0
直线上任意点
纵坐标都等于y0
O
l 的方程就是
思考:x轴所在直线的方程是什么?
②当直线 l 与x轴重合时,直线的方程是:y=0
y=0
①当直线 l 与x轴平行时:
(1)当直线 l 的倾斜角为0°时
x
y
l
P0(x0,y0)
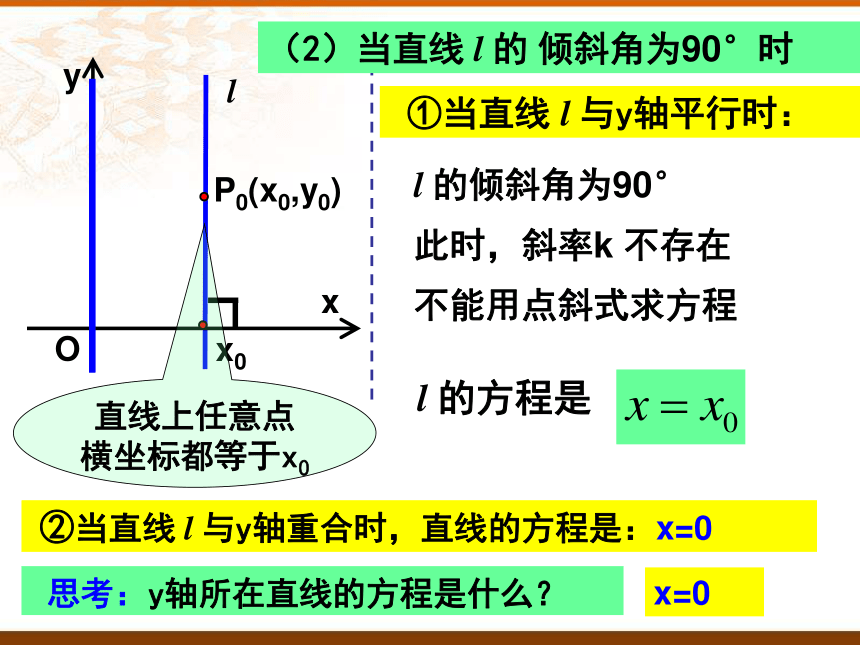
l 的倾斜角为90°
此时,斜率k 不存在
不能用点斜式求方程
x0
直线上任意点
横坐标都等于x0
O
l 的方程是
(2)当直线 l 的 倾斜角为90°时
思考:y轴所在直线的方程是什么?
x=0
②当直线 l 与y轴重合时,直线的方程是:x=0
①当直线 l 与y轴平行时:
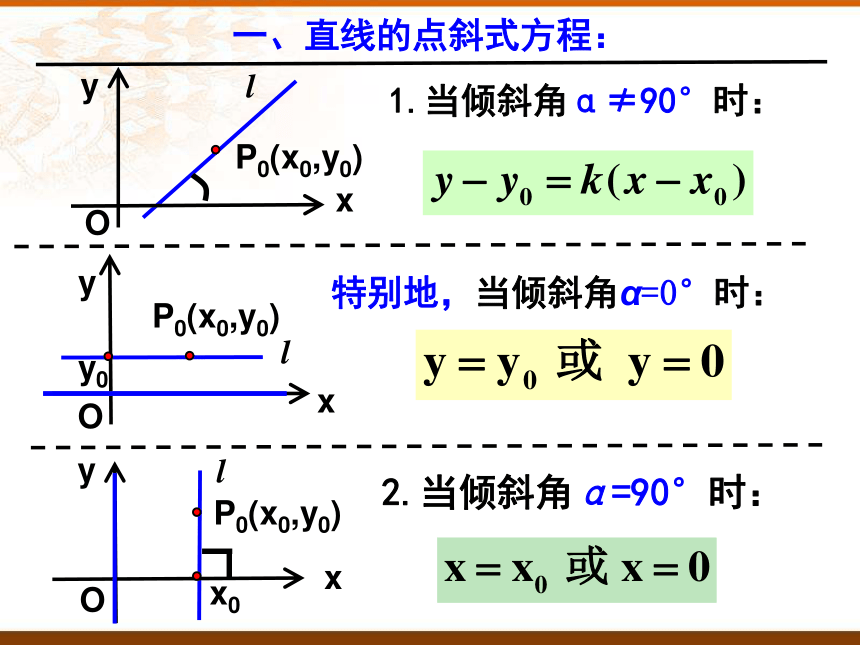
一、直线的点斜式方程:
x
y
l
x
y
l
x
y
l
O
1.当倾斜角α≠90°时:
特别地,当倾斜角α=0°时:
2.当倾斜角α=90°时:
y0
x0
P0(x0,y0)
P0(x0,y0)
P0(x0,y0)
O
O
2、填空题
(1)已知直线的点斜式方程是
,那么此直线的斜率是_______,倾斜角是__________。
(2)已知直线点斜式方程是
,那么此直线的斜率是_______,倾斜角是____________。
1
请看课本P62:练习2
例1:直线 l 过点 ,且倾斜角 ,求直线 l 的点斜式方程,并画出直线 l .
代入点斜式方程得: .
画图时,只需再找出直线 上的另一点 ,例如,取 ,得 的坐标为 ,过 的直线即为所求,如图示.
解:直线 l 经过点 ,斜率 ,
y
1
2
3
4
x
O
-1
-2
l
1、写出下列直线的点斜式方程:
(1)经过点A(3,-1),斜率是 ;
(2)经过点B( ,2),倾斜角是30°
(3)经过点C(0,3),倾斜角是0°
(4)经过点D(-4,-2),倾斜角是120°
你都作对了吗?
请看课本P61:练习1
2.2.1 直线的点斜式方程
第二课时
O
x
y
.
(0,b)
二、直线的斜截式方程:
已知直线 l 的斜率是k,与y轴的交点是P(0,b),求直线方程。
代入点斜式方程,得 l 的直线方程:
y-b = k(x-0)
即 y = kx+b
(2)
直线 l 与y轴交点(0,b)的纵坐标 b 叫做直线l 在y轴上的截距。
方程(2)是由直线的斜率k与它在y轴上的截距b确定,所以方程(2)叫做直线的斜截式方程,简称斜截式。
x
y
P0(0,b)
设直线经过点P0( 0 ,b),其斜率为k,求直线方程。
斜截式
斜率
截距
当知道斜率和截距时用斜截式
直线的斜截式方程
直线的斜截式方程:y = k x + b
其中,直线 l 与y轴交点(0,b)的纵坐标 b叫做直线 l 在y轴上的截距。
思考:截距是距离吗?
答:不是,截距可以是正数、负数或零,但距离只能是正数或零。例如直线y=2x-3在y轴上的截距是 -3。
3.写出下列直线的斜截式方程:
斜截式方程: y=kx+b 几何意义:k是直线的斜率,b是直线在y轴上的截距
请看课本P62:练习
直线的斜截式方程与一次函数的关系:
解析式相同,都是 y=kx+b
2.不同点:
(1)斜截式方程:k∈R
(2)一次函数:k≠0
1.相同点:
k的取值范围不同
例2:已知直线l1:y=k1x+b1,l2:y=k2x+b2 ,试讨论:
(1)l1 // l2 的条件是什么?
(2)l1⊥l2 的条件是什么?
1.点斜式方程:
当知道斜率k和一点坐标时用点斜式
3.斜截式方程:
当知道斜率k和截距b时用斜截式
2.特殊情况:
①直线和x轴平行时,倾斜角α=0°
②直线与x轴垂直时,倾斜角α=90°
三、小结
4、判断下列各对直线是否平行或垂直:
请看课本P62:练习
解:(1)平行;(2)垂直
1.在平面直角坐标系中,下列四个结论:
①每一条直线都有点斜式和斜截式方程;
②倾斜角是钝角的直线,斜率为负数;
③方程 与方程y+1=k(x-2)可表示同一条直线;
④直线过点P(x0,y0),倾斜角为90°,则其方程为x=x0
其中正确的个数为( )
A.1 B.2 C.3 D.4
B
学以致用:
3.已知直线 l1:y=2x+3a,l2:y=(a2+1)x+3,若 l1∥l2,则a=( )
A.0 B.-1 C.1 D.±1
A
B
4.已知直线 l 的方程为y-m=(m-1)(x+1),若 l 在y轴上的截距为7,则m=________.
4
学以致用:
5.直线l 的倾斜角为30°,点P(2,1)在直线l上,直线l 绕点P(2,1)按逆时针方向旋转30°后到达直线l1的位置,且直线l1与l2平行,l2是线段AB的垂直平分线,A(1,m-1),B(m,2),试求m的值.
如果直线l1,l2的斜率为k1,k2,那么
注:两直线不重合且斜率都存在时
1.l1∥l2 k1=k2
学以致用:
6.直线y=x+1绕其与y轴交点旋转90°的直线方程是______________
7.直线y=2x-4绕着它与x轴的交点逆时针旋转90°后,所得的直线方程为____________
y=-x+1
8.求下列直线的斜截式方程:
(2)在y轴上的截距为2,且与x轴平行;
(3)求倾斜角为150°,与y轴的交点到原点的距离为3的直线方程.
学以致用:
如果直线l1,l2的斜率为k1,k2. 那么:
*若两直线倾斜角都为90°,则两直线互相平行.
l1∥l2或l1与l2重合 k1=k2或l1与l2的斜率均不存在
综上得:
2.两直线的斜率都不存在时:
1.两直线不重合且斜率都存在时:
l1∥l2 k1=k2
(用斜率证明三点共线时,常用这个结论)
(一)两直线平行的判定
温故而知新
2.特殊情况下的两直线垂直:
若一条直线没有斜率,另一条直线的斜率为0,则两条直线互相垂直
综上得,
如果直线l1,l2的斜率为k1,k2 ,那么
1.两直线斜率都存在时:
(二)两直线垂直的判定
温故而知新
2.2.1 直线的点斜式方程
1.如何确定一条直线?
答:(1)已知两点可以确定一条直线。
(2)已知直线上的一点和直线的倾斜角(斜率)可以确定一条直线。
复习引入:
4.斜率公式:
3.直线的斜率定义:
2.直线的倾斜角定义及其范围:
直线 l 经过点P0(x0,y0),且斜率为k,设点 P(x,y)是直线 l 上不同于点P0的任意一点,因为直线 l 的斜率为k,由斜率公式得:
即
x
y
O
l
P0
P
问题引入:
(1)直线l 上每一个点的坐标都满足关系式y-y0=k(x-x0);
(2)坐标满足y-y0=k(x-x0)的每一个点都在直线l上.
说明:斜率要存在!
(x0,y0)
(x,y)
方程y-y0=k(x-x0)由直线上一个定点(x0,y0)及该直线的斜率k确定,我们把它叫做直线的点斜式方程,简称点斜式.
一、直线的点斜式方程
x
y
O
l
P0
直线的点斜式方程的前提条件:
①斜率必须存在;
②已知一点P0(x0,y0)和斜率k.
x
y
l
P0(x0 , y0)
l 的 倾斜角为0°,
,斜率k=0
y0
直线上任意点
纵坐标都等于y0
O
l 的方程就是
思考:x轴所在直线的方程是什么?
②当直线 l 与x轴重合时,直线的方程是:y=0
y=0
①当直线 l 与x轴平行时:
(1)当直线 l 的倾斜角为0°时
x
y
l
P0(x0,y0)
l 的倾斜角为90°
此时,斜率k 不存在
不能用点斜式求方程
x0
直线上任意点
横坐标都等于x0
O
l 的方程是
(2)当直线 l 的 倾斜角为90°时
思考:y轴所在直线的方程是什么?
x=0
②当直线 l 与y轴重合时,直线的方程是:x=0
①当直线 l 与y轴平行时:
一、直线的点斜式方程:
x
y
l
x
y
l
x
y
l
O
1.当倾斜角α≠90°时:
特别地,当倾斜角α=0°时:
2.当倾斜角α=90°时:
y0
x0
P0(x0,y0)
P0(x0,y0)
P0(x0,y0)
O
O
2、填空题
(1)已知直线的点斜式方程是
,那么此直线的斜率是_______,倾斜角是__________。
(2)已知直线点斜式方程是
,那么此直线的斜率是_______,倾斜角是____________。
1
请看课本P62:练习2
例1:直线 l 过点 ,且倾斜角 ,求直线 l 的点斜式方程,并画出直线 l .
代入点斜式方程得: .
画图时,只需再找出直线 上的另一点 ,例如,取 ,得 的坐标为 ,过 的直线即为所求,如图示.
解:直线 l 经过点 ,斜率 ,
y
1
2
3
4
x
O
-1
-2
l
1、写出下列直线的点斜式方程:
(1)经过点A(3,-1),斜率是 ;
(2)经过点B( ,2),倾斜角是30°
(3)经过点C(0,3),倾斜角是0°
(4)经过点D(-4,-2),倾斜角是120°
你都作对了吗?
请看课本P61:练习1
2.2.1 直线的点斜式方程
第二课时
O
x
y
.
(0,b)
二、直线的斜截式方程:
已知直线 l 的斜率是k,与y轴的交点是P(0,b),求直线方程。
代入点斜式方程,得 l 的直线方程:
y-b = k(x-0)
即 y = kx+b
(2)
直线 l 与y轴交点(0,b)的纵坐标 b 叫做直线l 在y轴上的截距。
方程(2)是由直线的斜率k与它在y轴上的截距b确定,所以方程(2)叫做直线的斜截式方程,简称斜截式。
x
y
P0(0,b)
设直线经过点P0( 0 ,b),其斜率为k,求直线方程。
斜截式
斜率
截距
当知道斜率和截距时用斜截式
直线的斜截式方程
直线的斜截式方程:y = k x + b
其中,直线 l 与y轴交点(0,b)的纵坐标 b叫做直线 l 在y轴上的截距。
思考:截距是距离吗?
答:不是,截距可以是正数、负数或零,但距离只能是正数或零。例如直线y=2x-3在y轴上的截距是 -3。
3.写出下列直线的斜截式方程:
斜截式方程: y=kx+b 几何意义:k是直线的斜率,b是直线在y轴上的截距
请看课本P62:练习
直线的斜截式方程与一次函数的关系:
解析式相同,都是 y=kx+b
2.不同点:
(1)斜截式方程:k∈R
(2)一次函数:k≠0
1.相同点:
k的取值范围不同
例2:已知直线l1:y=k1x+b1,l2:y=k2x+b2 ,试讨论:
(1)l1 // l2 的条件是什么?
(2)l1⊥l2 的条件是什么?
1.点斜式方程:
当知道斜率k和一点坐标时用点斜式
3.斜截式方程:
当知道斜率k和截距b时用斜截式
2.特殊情况:
①直线和x轴平行时,倾斜角α=0°
②直线与x轴垂直时,倾斜角α=90°
三、小结
4、判断下列各对直线是否平行或垂直:
请看课本P62:练习
解:(1)平行;(2)垂直
1.在平面直角坐标系中,下列四个结论:
①每一条直线都有点斜式和斜截式方程;
②倾斜角是钝角的直线,斜率为负数;
③方程 与方程y+1=k(x-2)可表示同一条直线;
④直线过点P(x0,y0),倾斜角为90°,则其方程为x=x0
其中正确的个数为( )
A.1 B.2 C.3 D.4
B
学以致用:
3.已知直线 l1:y=2x+3a,l2:y=(a2+1)x+3,若 l1∥l2,则a=( )
A.0 B.-1 C.1 D.±1
A
B
4.已知直线 l 的方程为y-m=(m-1)(x+1),若 l 在y轴上的截距为7,则m=________.
4
学以致用:
5.直线l 的倾斜角为30°,点P(2,1)在直线l上,直线l 绕点P(2,1)按逆时针方向旋转30°后到达直线l1的位置,且直线l1与l2平行,l2是线段AB的垂直平分线,A(1,m-1),B(m,2),试求m的值.
如果直线l1,l2的斜率为k1,k2,那么
注:两直线不重合且斜率都存在时
1.l1∥l2 k1=k2
学以致用:
6.直线y=x+1绕其与y轴交点旋转90°的直线方程是______________
7.直线y=2x-4绕着它与x轴的交点逆时针旋转90°后,所得的直线方程为____________
y=-x+1
8.求下列直线的斜截式方程:
(2)在y轴上的截距为2,且与x轴平行;
(3)求倾斜角为150°,与y轴的交点到原点的距离为3的直线方程.
学以致用:
