数学人教A版(2019)选择性必修第一册2.1.1 倾斜角与斜率(共23张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.1.1 倾斜角与斜率(共23张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-21 18:30:49 | ||
图片预览



文档简介
(共23张PPT)
2.1.1 倾斜角与斜率
2.1 直线的倾斜角与斜率
两个点
问题4:请分别指出这些直线共同点和区别?
不可以
共同点:它们都经过点P.
区别:它们的倾斜程度不同.
问题2:在平面直角坐标系内,确定直线的位置,需要哪些几何元素呢?
问题3:一点可以确定一条直线的位置吗?
问题1:对于一次函数y=x+1,它的图像是什么?你又是怎样确定它的图象
y
1
x
o
-1
一条直线
y
x
o
P
一点和一个方向也可以确定一条直线
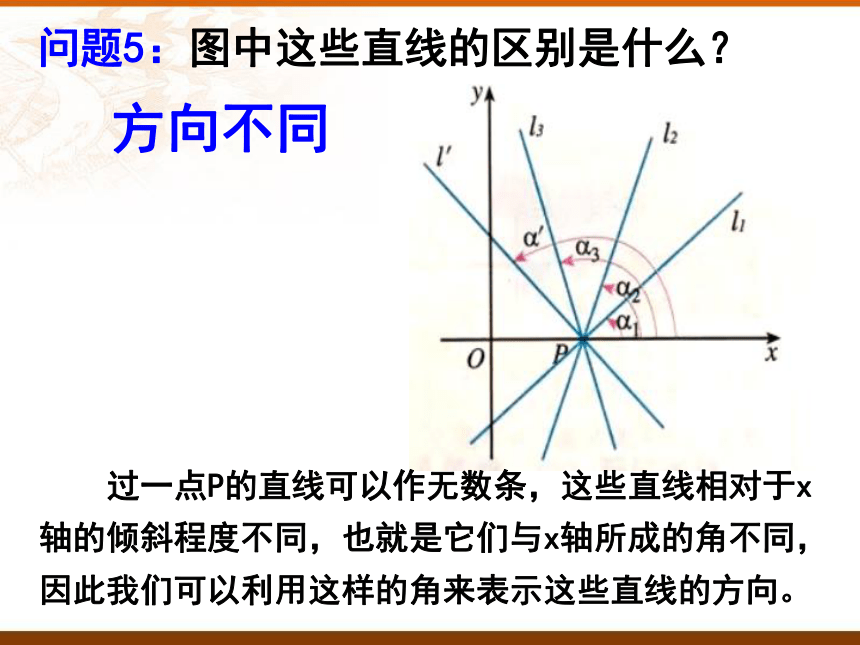
问题5:图中这些直线的区别是什么?
过一点P的直线可以作无数条,这些直线相对于x轴的倾斜程度不同,也就是它们与x轴所成的角不同,因此我们可以利用这样的角来表示这些直线的方向。
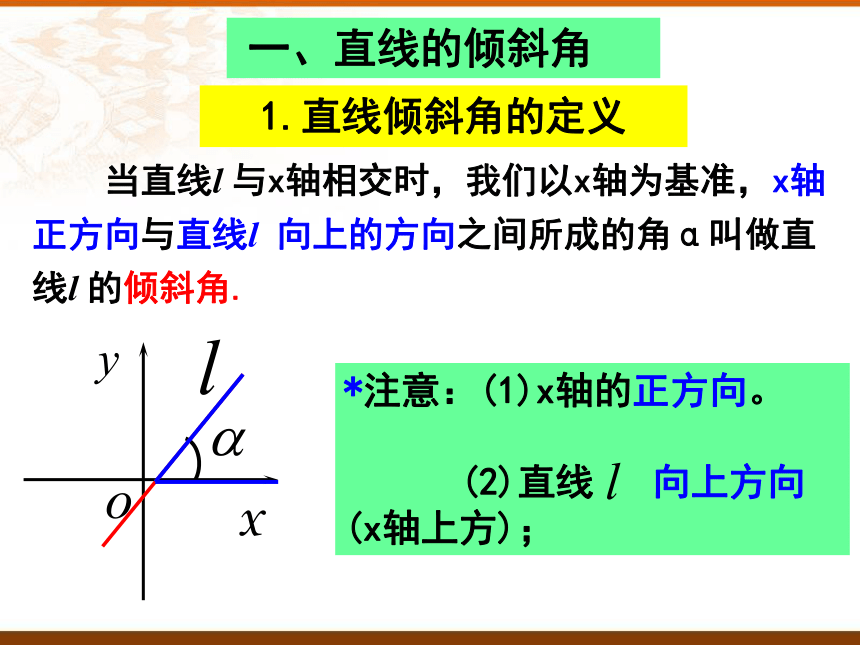
1.直线倾斜角的定义
*注意:(1)x轴的正方向。
(2)直线 向上方向(x轴上方);
当直线l 与x轴相交时,我们以x轴为基准,x轴正方向与直线l 向上的方向之间所成的角α叫做直线l 的倾斜角.
一、直线的倾斜角
2.直线倾斜角的范围
零度角
锐角
直角
钝角
直线的倾斜角可分为几类?
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
当直线 与 轴平行或重合时,我们规定它的倾斜角为 ,因此,直线的倾斜角的取值范围为:
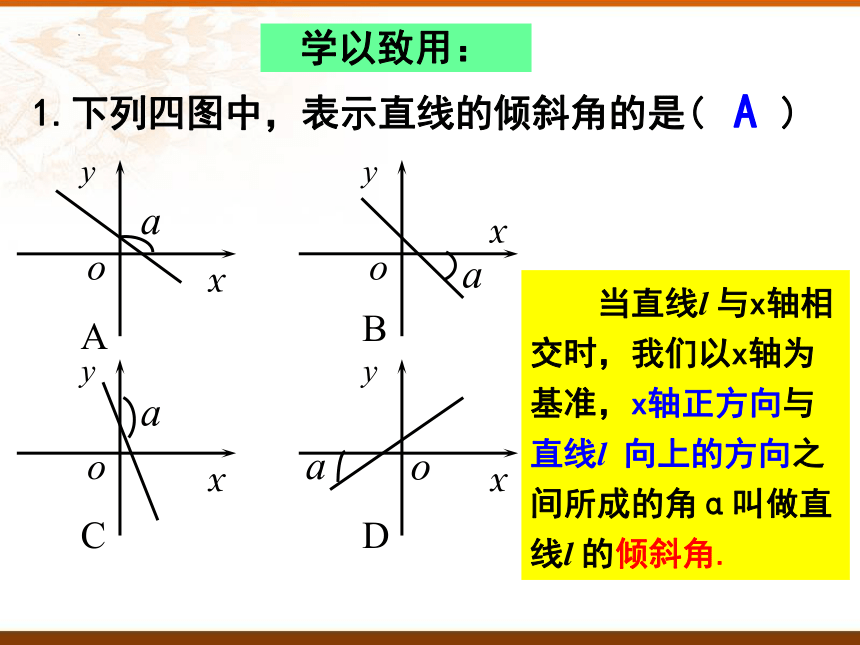
1.下列四图中,表示直线的倾斜角的是( )
学以致用:
A
B
C
D
A
当直线l 与x轴相交时,我们以x轴为基准,x轴正方向与直线l 向上的方向之间所成的角α叫做直线l 的倾斜角.
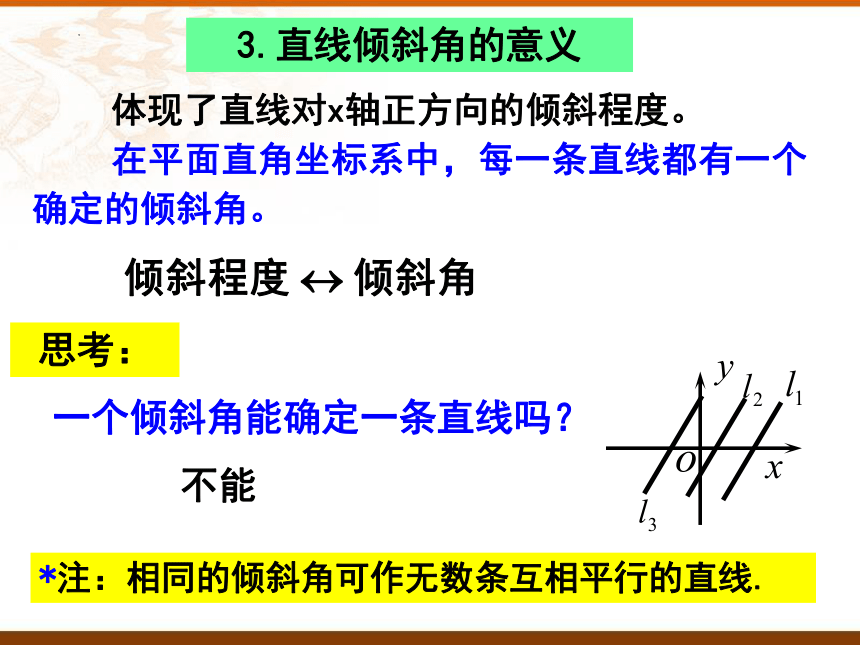
3.直线倾斜角的意义
体现了直线对x轴正方向的倾斜程度。
在平面直角坐标系中,每一条直线都有一个确定的倾斜角。
一个倾斜角能确定一条直线吗?
*注:相同的倾斜角可作无数条互相平行的直线.
思考:
不能
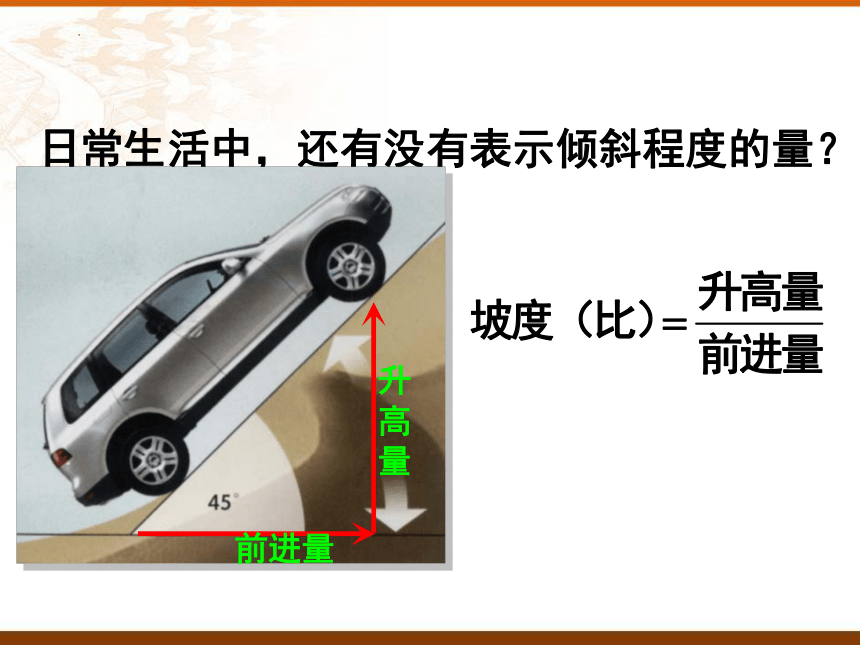
日常生活中,还有没有表示倾斜程度的量?
前进量
升
高
量
·
当直线平行于x轴,或与x轴重合时,上述公式还成立吗?为什么?
成立,因为分子为0,分母不为0
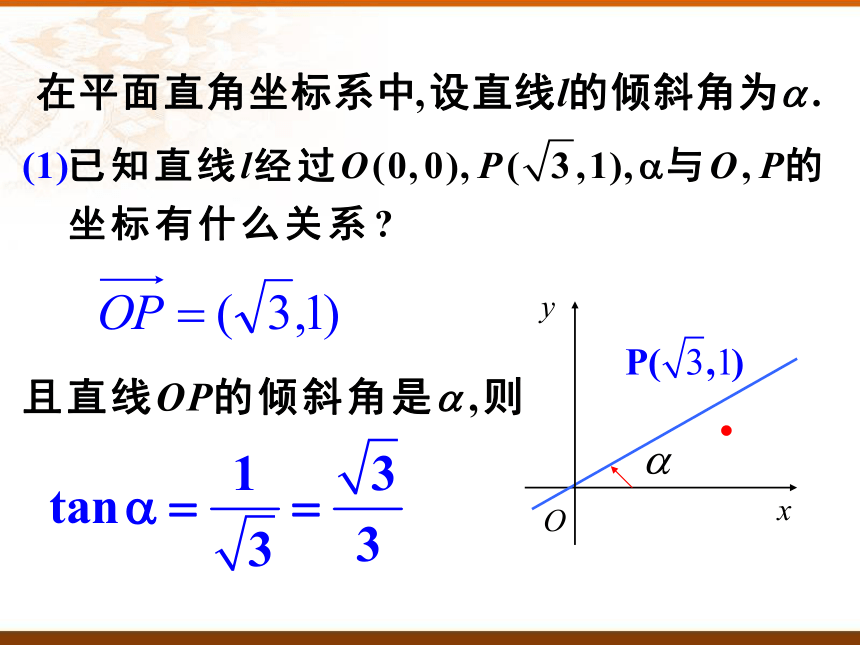
我们把一条直线的倾斜角α的正切值叫做这条直线的斜率.斜率常用小写字母k表示,即
我们也可以用斜率表示倾斜角不等于90°的直线相对于x轴的倾斜程度,进而表示直线的方向。
1.直线斜率的定义
例如:
二、直线的斜率
思考:当直线与 轴垂直时,直线的倾斜角是多少?
x
y
o
小结:倾斜角α不是 的直线都有斜率;倾斜角不同,直线的斜率也不同. 因此,我们可以用斜率表示直线的倾斜程度.
综上所述,我们得到经过两点
的直线的斜率公式:
2.直线的斜率公式
①
②
2.直线的斜率公式
答:与A、B两点的顺序无关。
思考:(2)当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?
斜率不存在,因为分母为0
= 0°
k=0
k>0
k不存在
k<0
倾斜角 斜率
= 90°
①当α∈[0°,90°)时, 倾斜角越大,斜率越大;
②当α∈(90°,180°)时,倾斜角越大,斜率越大.
0
判断正误:
①直线 l 的倾斜角为 ,则斜率为
②任一条直线都有倾斜角,但不一定有斜率。
×
√
x
y
o
例1:如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜 角是锐角还是钝角。
O
x
y
A (3,2)
C(0,-1)
B (-4,1)
请看课本P55:练习
2.求经过以下两点直线的斜率和倾斜角
(2)P(1,0),Q(0,1)
(1)A(0,0),B(1,1)
学以致用:
3.
X
Y
O
C
1.确定直线位置关系的要素
2.刻画直线倾斜程度的量
倾斜角、 斜率
3.数形结合、分类讨论、从特殊到一般的数学思想.
三、课堂小结
2.1.1 倾斜角与斜率
2.1 直线的倾斜角与斜率
两个点
问题4:请分别指出这些直线共同点和区别?
不可以
共同点:它们都经过点P.
区别:它们的倾斜程度不同.
问题2:在平面直角坐标系内,确定直线的位置,需要哪些几何元素呢?
问题3:一点可以确定一条直线的位置吗?
问题1:对于一次函数y=x+1,它的图像是什么?你又是怎样确定它的图象
y
1
x
o
-1
一条直线
y
x
o
P
一点和一个方向也可以确定一条直线
问题5:图中这些直线的区别是什么?
过一点P的直线可以作无数条,这些直线相对于x轴的倾斜程度不同,也就是它们与x轴所成的角不同,因此我们可以利用这样的角来表示这些直线的方向。
1.直线倾斜角的定义
*注意:(1)x轴的正方向。
(2)直线 向上方向(x轴上方);
当直线l 与x轴相交时,我们以x轴为基准,x轴正方向与直线l 向上的方向之间所成的角α叫做直线l 的倾斜角.
一、直线的倾斜角
2.直线倾斜角的范围
零度角
锐角
直角
钝角
直线的倾斜角可分为几类?
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
当直线 与 轴平行或重合时,我们规定它的倾斜角为 ,因此,直线的倾斜角的取值范围为:
1.下列四图中,表示直线的倾斜角的是( )
学以致用:
A
B
C
D
A
当直线l 与x轴相交时,我们以x轴为基准,x轴正方向与直线l 向上的方向之间所成的角α叫做直线l 的倾斜角.
3.直线倾斜角的意义
体现了直线对x轴正方向的倾斜程度。
在平面直角坐标系中,每一条直线都有一个确定的倾斜角。
一个倾斜角能确定一条直线吗?
*注:相同的倾斜角可作无数条互相平行的直线.
思考:
不能
日常生活中,还有没有表示倾斜程度的量?
前进量
升
高
量
·
当直线平行于x轴,或与x轴重合时,上述公式还成立吗?为什么?
成立,因为分子为0,分母不为0
我们把一条直线的倾斜角α的正切值叫做这条直线的斜率.斜率常用小写字母k表示,即
我们也可以用斜率表示倾斜角不等于90°的直线相对于x轴的倾斜程度,进而表示直线的方向。
1.直线斜率的定义
例如:
二、直线的斜率
思考:当直线与 轴垂直时,直线的倾斜角是多少?
x
y
o
小结:倾斜角α不是 的直线都有斜率;倾斜角不同,直线的斜率也不同. 因此,我们可以用斜率表示直线的倾斜程度.
综上所述,我们得到经过两点
的直线的斜率公式:
2.直线的斜率公式
①
②
2.直线的斜率公式
答:与A、B两点的顺序无关。
思考:(2)当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?
斜率不存在,因为分母为0
= 0°
k=0
k>0
k不存在
k<0
倾斜角 斜率
= 90°
①当α∈[0°,90°)时, 倾斜角越大,斜率越大;
②当α∈(90°,180°)时,倾斜角越大,斜率越大.
0
判断正误:
①直线 l 的倾斜角为 ,则斜率为
②任一条直线都有倾斜角,但不一定有斜率。
×
√
x
y
o
例1:如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜 角是锐角还是钝角。
O
x
y
A (3,2)
C(0,-1)
B (-4,1)
请看课本P55:练习
2.求经过以下两点直线的斜率和倾斜角
(2)P(1,0),Q(0,1)
(1)A(0,0),B(1,1)
学以致用:
3.
X
Y
O
C
1.确定直线位置关系的要素
2.刻画直线倾斜程度的量
倾斜角、 斜率
3.数形结合、分类讨论、从特殊到一般的数学思想.
三、课堂小结
