6.3实数 课件(2课时)
文档属性
| 名称 | 6.3实数 课件(2课时) |  | |
| 格式 | zip | ||
| 文件大小 | 595.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-08-06 17:35:13 | ||
图片预览









文档简介
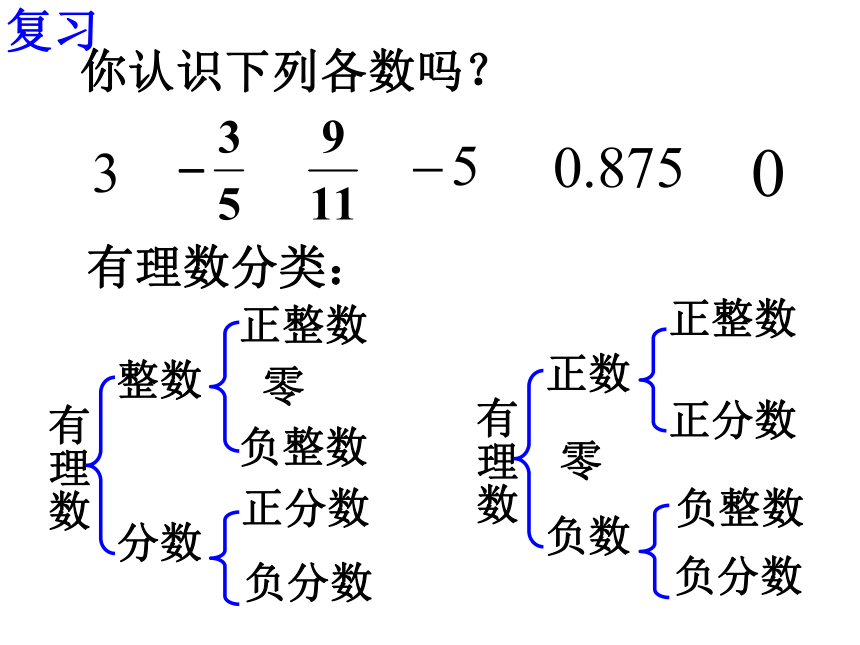
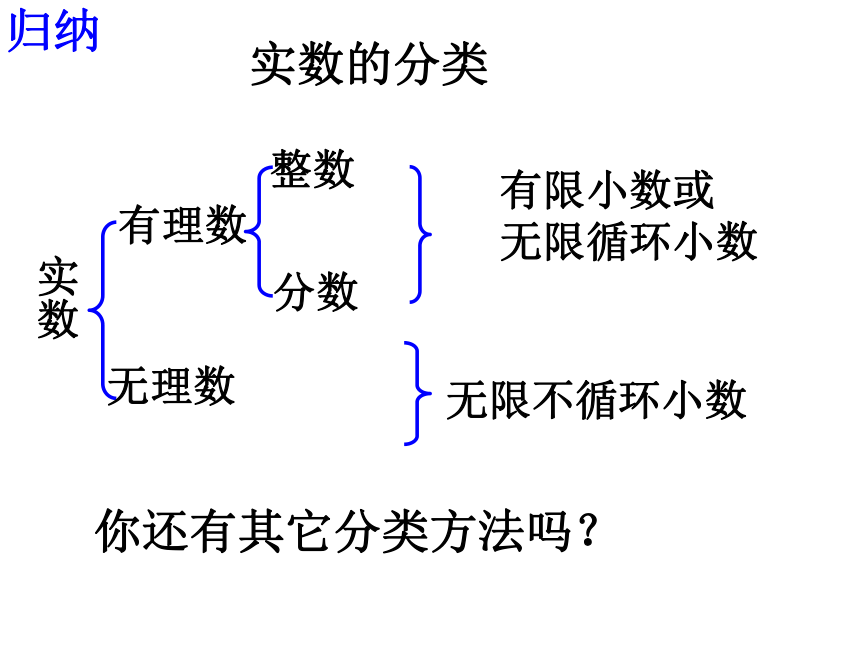
课件38张PPT。初中数学同步教学课件人教新课标 七年级下人教版七年级(下册)第六章实数6.3实数(第一课时)复习你认识下列各数吗?有理数分类:引入把下列各数写成小数的形式:有限小数无限循环小数有限小数和无限循环小数都是有理数任何一个有理数都可写成有限小数和无限循环小数的形式.探究把下列各数写成小数的形式:无限不循环小数无限不循环小数叫无理数有理数和无理数统称为实数归纳实数的分类实数有理数无理数整数分数有限小数或
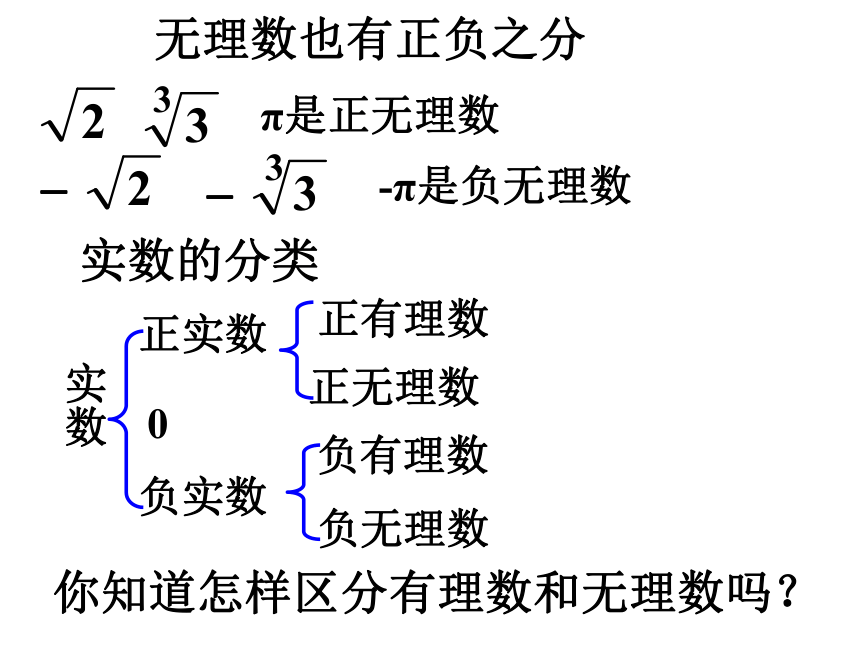
无限循环小数无限不循环小数你还有其它分类方法吗?实数正实数负实数正有理数正无理数你知道怎样区分有理数和无理数吗?0负无理数负有理数无理数也有正负之分例1、下列各数中,哪些是有理数,哪
些是无理数?1.圆周率2.开不尽的方根3.人为构造的数常见的无理数有以下三类:1、下列各数 , , , , ,
中,有理数的个数有( )
A 2个 B 3个 C 4个 D 5个2、在 , , ,
, 中,无理数分别
是 。C3. 判断题1. 无理数是无限小数,无限小数就是无理数2. 无理数包括正无理数,0,负无理数.3. 带根号的数都是无理数,不带根号的数
都是有理数×××4. 是一个分数.×3、把下列各数分别填在相应的集合中:有理数集合无理数集合……巩固 4、下列命题错误的是( )
A.有最小的正数
B.没有最大的有理数
C.有绝对值最小的数
D.正分数既是有理数又是实数5、下列结论正确的是( )
A.无限小数是无理数
B.有理数都可以表示成分数形式
C.无理数都是带根号的数
D.无理数都是无限不循环小数AD引入在数轴上表示下列各数:有理数都可以用数轴上的点表示探究 直径为1个单位长度的圆从原点沿
数轴向右滚动一周,圆上的一点由原点
到达O′,点O′的坐标是多少?O 1 2 3 4O′无理数π可以用数轴上的点表示O′的坐标是OO′=π π 1. 画一个直角三角形,使它的两条直角边
分别是3cm和4cm;2. 用直尺量出斜边的长;活动3. 这三条边的平方之间有什么关系?5cm32+42=52直角三角形的两条直角边
的平方和等于斜边的平方4. 在数轴上做出表示 的点。 以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正半轴的交点表示什么?无理数 可以用数轴上的点表示归纳 1、每一个有理数都可以用数轴上的点
表示;2、每一个无理数都可以用数轴上的点
表示;每一个实数都可用数轴上的点来表示;实数与数轴上的点是一一对应的数轴上的每一个点都表示一个实数;的相反数是 ;的相反数是 ;的相反数是 ;a的相反数是-a正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.绝对值等于 的数是什么?例1、(1)求 的绝对值;
(2)已知一个数的绝对值是 ,
求这个数。2、请将数轴上是各点与下列实数对应
起来:ABCDE1、下列各数中,互为相反数的是( )
A 与 B 与
C 与 D 与2、 的值是( )
A B C D3、在数轴上距离表示-2的点是 个
单位长度的数是 。CC4. - 是 的相反数。π-3.14的相反
数是 。3.14-π1、设 对应数轴上的点是A, 对应数轴上的点是B,那么A、B间的距离是 。2、在数轴上与原点的距离是 的点所表示的数是 。3、求下列各数的相反数:4、求下列各数的绝对值:一、判断:1.实数不是有理数就是无理数。( )2.无理数都是无限不循环小数。( )3.无理数都是无限小数。( )4.带根号的数都是无理数。( )5.无理数一定都带根号。( )6.两个无理数之积不一定是无理数。( )7.两个无理数之和一定是无理数。( )×××练一练把下列各数填入相应的集合内:(1)有理数集合:{(2)无理数集合:{(3)整数集合:{(4)负数集合:{(5)分数集合:{(6)实数集合:{}}}}}}……请谈谈你的收获小结1、本节课你学了什么知识?实数的定义实数的分类实数与数轴上的点是一一对应的有理数无理数有限小数或
无限循环小数无限不循环小数人教版七年级(下册)第六章实数6.3实数(第二课时)复习实数的分类实数有理数无理数整数分数有限小数或
无限循环小数无限不循环小数复习实数的分类实数正实数负实数正有理数正无理数0负无理数负有理数引入合并算术平方根性质乘法交换律
结合律范例例1、计算下列各式的值:(2)(1)注意:(1)计算题解题格式;(2)根指数、被开方数都分别相
同的无理数要合并。巩固1、计算:(1)(2)(3)范例例2、计算:(1)(2)注意:(1)先去括号、绝对值;(2)再合并。巩固2、计算:(1)(2)探究 例3、计算:(1) (精确到0.01)(2) (结果保留3个有效数字)注意:(1)无理数近似值多取1位;(2)结果按要求取近似值。巩固 3、计算:(1) (精确到0.01)(2) (保留3个有效数字)范例例4、解方程:(1)(2)注意:(1)将括号看作一个整体;(2)开平方有两个值,开立方只
有一个值。(3)巩固5、解方程:(1)(2)(3)……请谈谈你的收获小结1、本节课你学了什么知识?2、你有什么体会?实数的计算方程的解法计算方法开方
无限循环小数无限不循环小数你还有其它分类方法吗?实数正实数负实数正有理数正无理数你知道怎样区分有理数和无理数吗?0负无理数负有理数无理数也有正负之分例1、下列各数中,哪些是有理数,哪
些是无理数?1.圆周率2.开不尽的方根3.人为构造的数常见的无理数有以下三类:1、下列各数 , , , , ,
中,有理数的个数有( )
A 2个 B 3个 C 4个 D 5个2、在 , , ,
, 中,无理数分别
是 。C3. 判断题1. 无理数是无限小数,无限小数就是无理数2. 无理数包括正无理数,0,负无理数.3. 带根号的数都是无理数,不带根号的数
都是有理数×××4. 是一个分数.×3、把下列各数分别填在相应的集合中:有理数集合无理数集合……巩固 4、下列命题错误的是( )
A.有最小的正数
B.没有最大的有理数
C.有绝对值最小的数
D.正分数既是有理数又是实数5、下列结论正确的是( )
A.无限小数是无理数
B.有理数都可以表示成分数形式
C.无理数都是带根号的数
D.无理数都是无限不循环小数AD引入在数轴上表示下列各数:有理数都可以用数轴上的点表示探究 直径为1个单位长度的圆从原点沿
数轴向右滚动一周,圆上的一点由原点
到达O′,点O′的坐标是多少?O 1 2 3 4O′无理数π可以用数轴上的点表示O′的坐标是OO′=π π 1. 画一个直角三角形,使它的两条直角边
分别是3cm和4cm;2. 用直尺量出斜边的长;活动3. 这三条边的平方之间有什么关系?5cm32+42=52直角三角形的两条直角边
的平方和等于斜边的平方4. 在数轴上做出表示 的点。 以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正半轴的交点表示什么?无理数 可以用数轴上的点表示归纳 1、每一个有理数都可以用数轴上的点
表示;2、每一个无理数都可以用数轴上的点
表示;每一个实数都可用数轴上的点来表示;实数与数轴上的点是一一对应的数轴上的每一个点都表示一个实数;的相反数是 ;的相反数是 ;的相反数是 ;a的相反数是-a正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.绝对值等于 的数是什么?例1、(1)求 的绝对值;
(2)已知一个数的绝对值是 ,
求这个数。2、请将数轴上是各点与下列实数对应
起来:ABCDE1、下列各数中,互为相反数的是( )
A 与 B 与
C 与 D 与2、 的值是( )
A B C D3、在数轴上距离表示-2的点是 个
单位长度的数是 。CC4. - 是 的相反数。π-3.14的相反
数是 。3.14-π1、设 对应数轴上的点是A, 对应数轴上的点是B,那么A、B间的距离是 。2、在数轴上与原点的距离是 的点所表示的数是 。3、求下列各数的相反数:4、求下列各数的绝对值:一、判断:1.实数不是有理数就是无理数。( )2.无理数都是无限不循环小数。( )3.无理数都是无限小数。( )4.带根号的数都是无理数。( )5.无理数一定都带根号。( )6.两个无理数之积不一定是无理数。( )7.两个无理数之和一定是无理数。( )×××练一练把下列各数填入相应的集合内:(1)有理数集合:{(2)无理数集合:{(3)整数集合:{(4)负数集合:{(5)分数集合:{(6)实数集合:{}}}}}}……请谈谈你的收获小结1、本节课你学了什么知识?实数的定义实数的分类实数与数轴上的点是一一对应的有理数无理数有限小数或
无限循环小数无限不循环小数人教版七年级(下册)第六章实数6.3实数(第二课时)复习实数的分类实数有理数无理数整数分数有限小数或
无限循环小数无限不循环小数复习实数的分类实数正实数负实数正有理数正无理数0负无理数负有理数引入合并算术平方根性质乘法交换律
结合律范例例1、计算下列各式的值:(2)(1)注意:(1)计算题解题格式;(2)根指数、被开方数都分别相
同的无理数要合并。巩固1、计算:(1)(2)(3)范例例2、计算:(1)(2)注意:(1)先去括号、绝对值;(2)再合并。巩固2、计算:(1)(2)探究 例3、计算:(1) (精确到0.01)(2) (结果保留3个有效数字)注意:(1)无理数近似值多取1位;(2)结果按要求取近似值。巩固 3、计算:(1) (精确到0.01)(2) (保留3个有效数字)范例例4、解方程:(1)(2)注意:(1)将括号看作一个整体;(2)开平方有两个值,开立方只
有一个值。(3)巩固5、解方程:(1)(2)(3)……请谈谈你的收获小结1、本节课你学了什么知识?2、你有什么体会?实数的计算方程的解法计算方法开方
