七年级上册期中综合测试题
图片预览



文档简介
中小学教育资源及组卷应用平台
七年级上册期中综合测试题
(满分:120分 时间:100分钟)
一、选择题(每小题3分,共36分)
1.下列图形中,不是轴对称图形的是( )
2.将一张等腰三角形纸片按如图①所示的方式对折,再沿如图②所示的虚线剪去一个小三角形,将余下的纸片展开得到的图形是( )
3.已知三角形的两边长分别为3cm和4cm,则该三角形的第三边长不可能是( )
4.以下列几组数为长度的线段不能构成直角三角形的是( )
5.在△ABC中,∠A=21°,∠B=34°,则△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
6.根据下列已知条件,能画出唯一的△的是( )
7.以下叙述中,不正确的是( )
A.等边三角形的每条高线都是角平分线和中线
B.有一个内角为60°的等腰三角形是等边三角形
C.等腰三角形一定是锐角三角形
D.在一个三角形中,如果两条边不相等,那么它们所对的角也不相等;反之,如果两个角不相等,那么它们所对的边也不相等
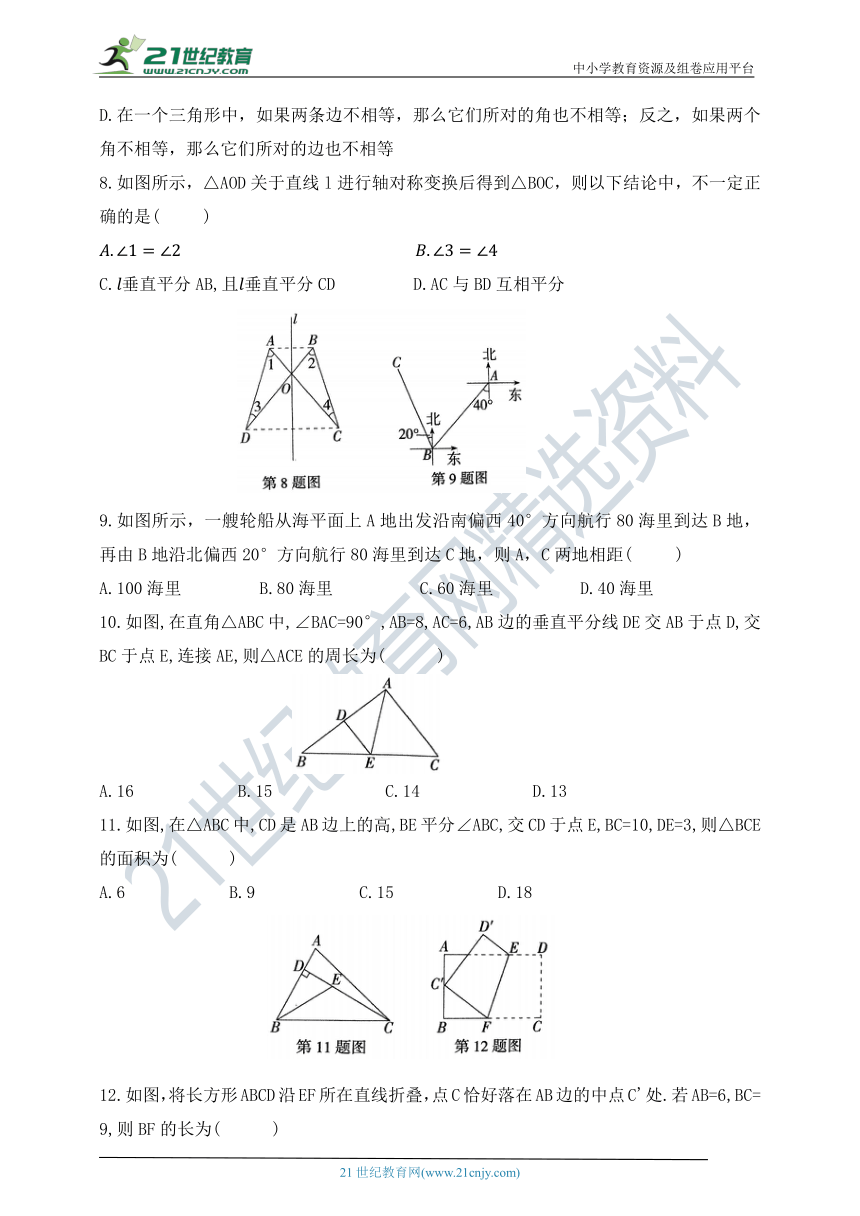
8.如图所示,△AOD关于直线l进行轴对称变换后得到△BOC,则以下结论中,不一定正确的是( )
C.垂直平分AB,且垂直平分CD D.AC与BD互相平分
9.如图所示,一艘轮船从海平面上A地出发沿南偏西40°方向航行80海里到达B地,再由B地沿北偏西20°方向航行80海里到达C地,则A,C两地相距( )
A.100海里 B.80海里 C.60海里 D.40海里
10.如图,在直角△ABC中,∠BAC=90°,AB=8,AC=6,AB边的垂直平分线DE交AB于点D,交
BC于点E,连接AE,则△ACE的周长为( )
A.16 B.15 C.14 D.13
11.如图,在△ABC中,CD是AB边上的高,BE平分∠ABC,交CD于点E,BC=10,DE=3,则△BCE的面积为( )
A.6 B.9 C.15 D.18
12.如图,将长方形ABCD沿EF所在直线折叠,点C恰好落在AB边的中点C'处.若AB=6,BC=
9,则BF的长为( )
A.3 B.4 C.4.5 D.5
二、填空题(每小题4分,共24分)
13.如图,AD是△ABC的中线,AE是△ABD的中线,若DE=3cm,则EC=___________cm.
14.如图是某商场一楼与二楼之间的手扶电梯的示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是___________m.
15.如图所示,在△ABC中,∠B=∠C=50°,BD=CF,BE=CD,则∠EDF的度数是__________.
16.如图,某自动感应门的正上方A处装着一个感应器,感应器离地面的高度AB=2.5米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高为1.6米的学生CD正对着门,缓慢走到离门1.2米的地方时(BC=1.2米),感应门自动打开,则AD=__________米.
17.等腰三角形ABC中, 一腰上的中线把这个三角形的周长分成12和15两部
分,则这个三角形的底边长为__________.
18.观察下列各组勾股数:①4,3,5;②6,8,10;③8,15,17;④10,24,26;……,分析上面各组勾股数可以发现,4=2×(1+1),6=2×(2+1),8=2×(3+1),……,请根据你发现的规律写出第⑦组勾股数:________________.
三、解答题(共60分)
19.(8分)如图所示,已知线段、m及 求作△ABC,使AB+BC=l,BC=m,∠A=∠α.(尺规
作图,不写作法,保留作图痕迹)
20.(10分)如图,已知四边形ABCD,如果点D、C关于直线MN对称.
(1)画出直线MN;
(2)画出与四边形ABCD关于直线MN成轴对称的图形.
21.(10分)如图,CE⊥AB于点E,E为AB的中点,AD=5,CD=4,BC=3,求证:∠ACD=90°.
22.(10分)如图,一条河流MN旁边有两个村庄A,B,AD⊥MN于D.由于有山阻挡,村庄B到
MN的距离不能直接测量,河边恰好有一点C能到达A,B两个村庄,且 C与A,B间的距离相等,测得C,D间的距离为150m,请求出村庄B到MN的距离.
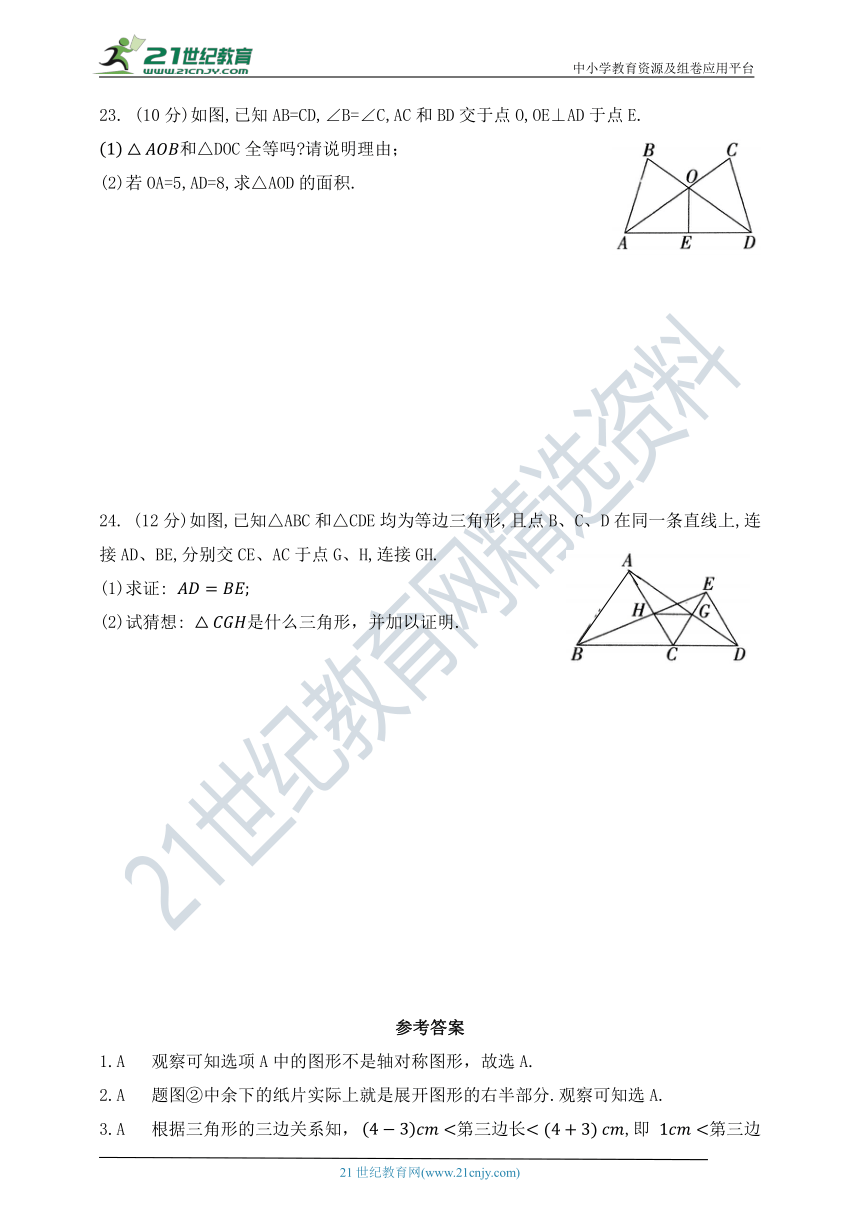
23. (10分)如图,已知AB=CD,∠B=∠C,AC和BD交于点O,OE⊥AD于点E.
和△DOC全等吗 请说明理由;
(2)若OA=5,AD=8,求△AOD的面积.
24. (12分)如图,已知△ABC和△CDE均为等边三角形,且点B、C、D在同一条直线上,连接AD、BE,分别交CE、AC于点G、H,连接GH.
(1)求证:
(2)试猜想: 是什么三角形,并加以证明.
参考答案
1.A 观察可知选项A中的图形不是轴对称图形,故选A.
2.A 题图②中余下的纸片实际上就是展开图形的右半部分.观察可知选A.
3.A 根据三角形的三边关系知, 第三边长,即 第三边长,故选A.
4.B 能构成直角三角形,故A不符合题意; 不能构成直角三角形,故B符合题意; 能构成直角三角形,故C不符合题意; 能构成直角三角形,故D不符合题意.故选B.
5.C 由题意得 是钝角三角形,故选C.
6.D 则AB,BC,CA不能构成三角形,所以A选项不符合题意;B.由∠C=90°,AB=6可以画出无数个三角形,所以B选项不符合题意;C.由AB=4,BC=3,∠A=30°不可以画出唯一的△ABC,所以C选项不符合题意;D.由 4可以画出唯一的△ABC,所以D选项符合题意.故选D.
7.C 等腰三角形可能是锐角三角形,直角三角形,钝角三角形,故选C.
8.D ∵△AOD关于直线进行轴对称变换后得到△BOC,∴∠1=∠2,∠3=∠4,垂直平分AB,且垂直平分CD,∴A、B、C中结论正确.故选D.
9.B 如图,连接AC.
∵点B在点A的南偏西40°方向上,点C在点B的北偏西 方向上,
又∵BC=BA=80海里,∴△ABC为等边三角形.∴AC=BC=AB=80海里.故选B.
10.A 在直角 中, 所以 所以BC=10,因为DE垂直平分AB,所以AE=BE,所以△ACE的周长=故选A.
11.C 如图,作EH⊥BC于H,
∵BE平分∠ABC,CD是AB边上的高,EH⊥BC,∴EH=DE=3,
∴△BCE的面积 10×3=15,故选C.
12.B ∵点是AB的中点, 由题意可知, 在直角三角形BF中, 解得BF=4,故选B.
13.答案 9
解析 ∵AE是△ABD的中线,,∴∵AD是△ABC的中线,∴,∴.
14.答案 4
解析 如图,过C作CE⊥AB于E,
即
15.答案 50°
解析 在△BDE和△CFD中
16.答案 1.5
解析 如图,过点D作DE⊥AB于点E,
由题意知 米, 米, 1.2米,∴ (米).
在Rt△ADE中,由勾股定理得 (米 ),∴AD=1.5米.
17.答案 7或11
解析 如图,△ABC是等腰三角形, 为底边,CD为△ABC的边AB上的中线,设则,
依题意,分以下两种情况:(1)则,解得,此时△ABC的三边长分别为10,10,7,符合三角形的三边关系.
(2),则 15,解得此时 的三边长分别为8,8,11,符合三角形的三边关系.
综上,这个三角形的底边长为7或11.
18.答案 16,63,65
解析 前4组勾股数中,第一个数分别是第二个数分别是 第三个数分别是故第 组勾股数中,第一个数是,第二个数是,第三个数是 所以第⑦组勾股数是16,63,65.
19.解析 如图所示, △ 为所求作的三角形.
20.解析 (1)如图所示,直线MN即为所求.
(2)如图,四边形即为与四边形ABCD关于直线MN成轴对称的图形.
21.证明 ∵CE⊥AB于点E,E为AB的中点,∴AC=BC,∵BC=3,∴AC=3,又∵AD=5,CD=4,∴AC +是直角三角形,∠ACD=90°.
22.解析 如图,过点B作BE⊥MN于点E,
由题意知∠BEC=∠ADC=∠ACB=90°,∴∠A+∠ACD=90°,∠ACD+∠BCE=90°,
∴∠A=∠BCE.
在△ADC和△CEB中, △ADC≌△CEB(AAS),∴BE=CD=150m,
故村庄B到MN的距离是150m.
23.解析 (1)△AOB和△DOC全等.
理由:在△AOB和△DOC中, 所以△
(2)因为△AOB≌△DOC,所以AO=DO,因为OE⊥AD于点E,所以 是直角
三角形,所以 所以OE=3,所以
24.解析 (1)证明:因为△和△均为等边三角形,所以 60°,所以
在△ACD和△BCE中, 所以△ACDE≌△BCE(SAS),所以AD=BE.
(2)△CGH是等边三角形.
证明:因为△所以
因为 点B、C、D在同一条直线上,
所以 所以∠BCH=∠ACG=60°,
在△ACG和△BCH中 所以△ACG≌△BCH(ASA),
所以 所以△是等边三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
七年级上册期中综合测试题
(满分:120分 时间:100分钟)
一、选择题(每小题3分,共36分)
1.下列图形中,不是轴对称图形的是( )
2.将一张等腰三角形纸片按如图①所示的方式对折,再沿如图②所示的虚线剪去一个小三角形,将余下的纸片展开得到的图形是( )
3.已知三角形的两边长分别为3cm和4cm,则该三角形的第三边长不可能是( )
4.以下列几组数为长度的线段不能构成直角三角形的是( )
5.在△ABC中,∠A=21°,∠B=34°,则△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
6.根据下列已知条件,能画出唯一的△的是( )
7.以下叙述中,不正确的是( )
A.等边三角形的每条高线都是角平分线和中线
B.有一个内角为60°的等腰三角形是等边三角形
C.等腰三角形一定是锐角三角形
D.在一个三角形中,如果两条边不相等,那么它们所对的角也不相等;反之,如果两个角不相等,那么它们所对的边也不相等
8.如图所示,△AOD关于直线l进行轴对称变换后得到△BOC,则以下结论中,不一定正确的是( )
C.垂直平分AB,且垂直平分CD D.AC与BD互相平分
9.如图所示,一艘轮船从海平面上A地出发沿南偏西40°方向航行80海里到达B地,再由B地沿北偏西20°方向航行80海里到达C地,则A,C两地相距( )
A.100海里 B.80海里 C.60海里 D.40海里
10.如图,在直角△ABC中,∠BAC=90°,AB=8,AC=6,AB边的垂直平分线DE交AB于点D,交
BC于点E,连接AE,则△ACE的周长为( )
A.16 B.15 C.14 D.13
11.如图,在△ABC中,CD是AB边上的高,BE平分∠ABC,交CD于点E,BC=10,DE=3,则△BCE的面积为( )
A.6 B.9 C.15 D.18
12.如图,将长方形ABCD沿EF所在直线折叠,点C恰好落在AB边的中点C'处.若AB=6,BC=
9,则BF的长为( )
A.3 B.4 C.4.5 D.5
二、填空题(每小题4分,共24分)
13.如图,AD是△ABC的中线,AE是△ABD的中线,若DE=3cm,则EC=___________cm.
14.如图是某商场一楼与二楼之间的手扶电梯的示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是___________m.
15.如图所示,在△ABC中,∠B=∠C=50°,BD=CF,BE=CD,则∠EDF的度数是__________.
16.如图,某自动感应门的正上方A处装着一个感应器,感应器离地面的高度AB=2.5米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高为1.6米的学生CD正对着门,缓慢走到离门1.2米的地方时(BC=1.2米),感应门自动打开,则AD=__________米.
17.等腰三角形ABC中, 一腰上的中线把这个三角形的周长分成12和15两部
分,则这个三角形的底边长为__________.
18.观察下列各组勾股数:①4,3,5;②6,8,10;③8,15,17;④10,24,26;……,分析上面各组勾股数可以发现,4=2×(1+1),6=2×(2+1),8=2×(3+1),……,请根据你发现的规律写出第⑦组勾股数:________________.
三、解答题(共60分)
19.(8分)如图所示,已知线段、m及 求作△ABC,使AB+BC=l,BC=m,∠A=∠α.(尺规
作图,不写作法,保留作图痕迹)
20.(10分)如图,已知四边形ABCD,如果点D、C关于直线MN对称.
(1)画出直线MN;
(2)画出与四边形ABCD关于直线MN成轴对称的图形.
21.(10分)如图,CE⊥AB于点E,E为AB的中点,AD=5,CD=4,BC=3,求证:∠ACD=90°.
22.(10分)如图,一条河流MN旁边有两个村庄A,B,AD⊥MN于D.由于有山阻挡,村庄B到
MN的距离不能直接测量,河边恰好有一点C能到达A,B两个村庄,且 C与A,B间的距离相等,测得C,D间的距离为150m,请求出村庄B到MN的距离.
23. (10分)如图,已知AB=CD,∠B=∠C,AC和BD交于点O,OE⊥AD于点E.
和△DOC全等吗 请说明理由;
(2)若OA=5,AD=8,求△AOD的面积.
24. (12分)如图,已知△ABC和△CDE均为等边三角形,且点B、C、D在同一条直线上,连接AD、BE,分别交CE、AC于点G、H,连接GH.
(1)求证:
(2)试猜想: 是什么三角形,并加以证明.
参考答案
1.A 观察可知选项A中的图形不是轴对称图形,故选A.
2.A 题图②中余下的纸片实际上就是展开图形的右半部分.观察可知选A.
3.A 根据三角形的三边关系知, 第三边长,即 第三边长,故选A.
4.B 能构成直角三角形,故A不符合题意; 不能构成直角三角形,故B符合题意; 能构成直角三角形,故C不符合题意; 能构成直角三角形,故D不符合题意.故选B.
5.C 由题意得 是钝角三角形,故选C.
6.D 则AB,BC,CA不能构成三角形,所以A选项不符合题意;B.由∠C=90°,AB=6可以画出无数个三角形,所以B选项不符合题意;C.由AB=4,BC=3,∠A=30°不可以画出唯一的△ABC,所以C选项不符合题意;D.由 4可以画出唯一的△ABC,所以D选项符合题意.故选D.
7.C 等腰三角形可能是锐角三角形,直角三角形,钝角三角形,故选C.
8.D ∵△AOD关于直线进行轴对称变换后得到△BOC,∴∠1=∠2,∠3=∠4,垂直平分AB,且垂直平分CD,∴A、B、C中结论正确.故选D.
9.B 如图,连接AC.
∵点B在点A的南偏西40°方向上,点C在点B的北偏西 方向上,
又∵BC=BA=80海里,∴△ABC为等边三角形.∴AC=BC=AB=80海里.故选B.
10.A 在直角 中, 所以 所以BC=10,因为DE垂直平分AB,所以AE=BE,所以△ACE的周长=故选A.
11.C 如图,作EH⊥BC于H,
∵BE平分∠ABC,CD是AB边上的高,EH⊥BC,∴EH=DE=3,
∴△BCE的面积 10×3=15,故选C.
12.B ∵点是AB的中点, 由题意可知, 在直角三角形BF中, 解得BF=4,故选B.
13.答案 9
解析 ∵AE是△ABD的中线,,∴∵AD是△ABC的中线,∴,∴.
14.答案 4
解析 如图,过C作CE⊥AB于E,
即
15.答案 50°
解析 在△BDE和△CFD中
16.答案 1.5
解析 如图,过点D作DE⊥AB于点E,
由题意知 米, 米, 1.2米,∴ (米).
在Rt△ADE中,由勾股定理得 (米 ),∴AD=1.5米.
17.答案 7或11
解析 如图,△ABC是等腰三角形, 为底边,CD为△ABC的边AB上的中线,设则,
依题意,分以下两种情况:(1)则,解得,此时△ABC的三边长分别为10,10,7,符合三角形的三边关系.
(2),则 15,解得此时 的三边长分别为8,8,11,符合三角形的三边关系.
综上,这个三角形的底边长为7或11.
18.答案 16,63,65
解析 前4组勾股数中,第一个数分别是第二个数分别是 第三个数分别是故第 组勾股数中,第一个数是,第二个数是,第三个数是 所以第⑦组勾股数是16,63,65.
19.解析 如图所示, △ 为所求作的三角形.
20.解析 (1)如图所示,直线MN即为所求.
(2)如图,四边形即为与四边形ABCD关于直线MN成轴对称的图形.
21.证明 ∵CE⊥AB于点E,E为AB的中点,∴AC=BC,∵BC=3,∴AC=3,又∵AD=5,CD=4,∴AC +是直角三角形,∠ACD=90°.
22.解析 如图,过点B作BE⊥MN于点E,
由题意知∠BEC=∠ADC=∠ACB=90°,∴∠A+∠ACD=90°,∠ACD+∠BCE=90°,
∴∠A=∠BCE.
在△ADC和△CEB中, △ADC≌△CEB(AAS),∴BE=CD=150m,
故村庄B到MN的距离是150m.
23.解析 (1)△AOB和△DOC全等.
理由:在△AOB和△DOC中, 所以△
(2)因为△AOB≌△DOC,所以AO=DO,因为OE⊥AD于点E,所以 是直角
三角形,所以 所以OE=3,所以
24.解析 (1)证明:因为△和△均为等边三角形,所以 60°,所以
在△ACD和△BCE中, 所以△ACDE≌△BCE(SAS),所以AD=BE.
(2)△CGH是等边三角形.
证明:因为△所以
因为 点B、C、D在同一条直线上,
所以 所以∠BCH=∠ACG=60°,
在△ACG和△BCH中 所以△ACG≌△BCH(ASA),
所以 所以△是等边三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
