3.9《圆柱与圆锥》整理复习课件六年级下册数学人教版(共39张PPT)
文档属性
| 名称 | 3.9《圆柱与圆锥》整理复习课件六年级下册数学人教版(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-21 14:46:03 | ||
图片预览




文档简介
(共39张PPT)
《圆柱与圆锥》整理和复习
小学数学-人教版-六年级下册-第三单元
电子教材
整
理
复
习
圆柱与圆锥
形成网络
梳理知识
巩固旧知
提升记忆
突破难点
纠正错误
灵活运用
综合拓展
知识分享
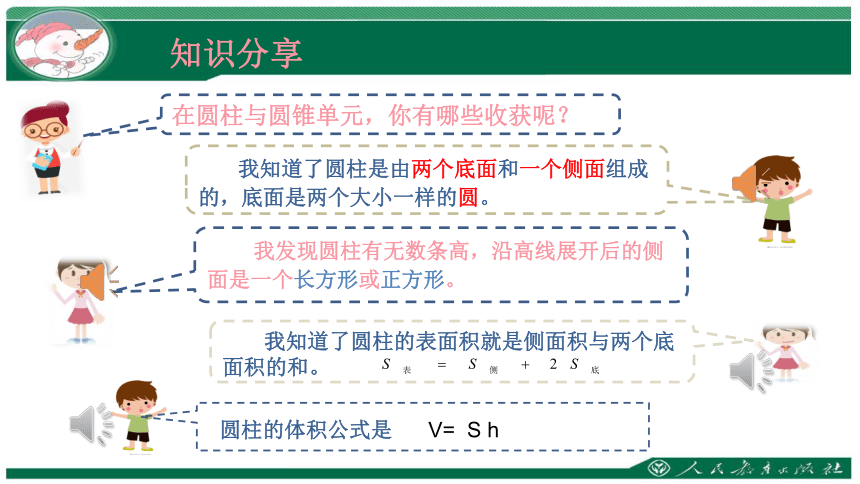
在圆柱与圆锥单元,你有哪些收获呢?
我知道了圆柱是由两个底面和一个侧面组成的,底面是两个大小一样的圆。
我发现圆柱有无数条高,沿高线展开后的侧面是一个长方形或正方形。
圆柱的体积公式是 V= S h
我知道了圆柱的表面积就是侧面积与两个底面积的和。
知识分享
你们知道圆锥有什么特征吗?它与圆柱之间有什么区别与联系?
我知道圆锥的底面是一个圆,侧面是一个曲面。从圆锥的顶点到底面圆心的距离是圆锥的高。因此它只有一条高,而圆柱有无数条高。圆锥只有一个底面,圆柱有两个底面。
圆锥的体积是与它等底等高的圆柱的体积的三分之一。
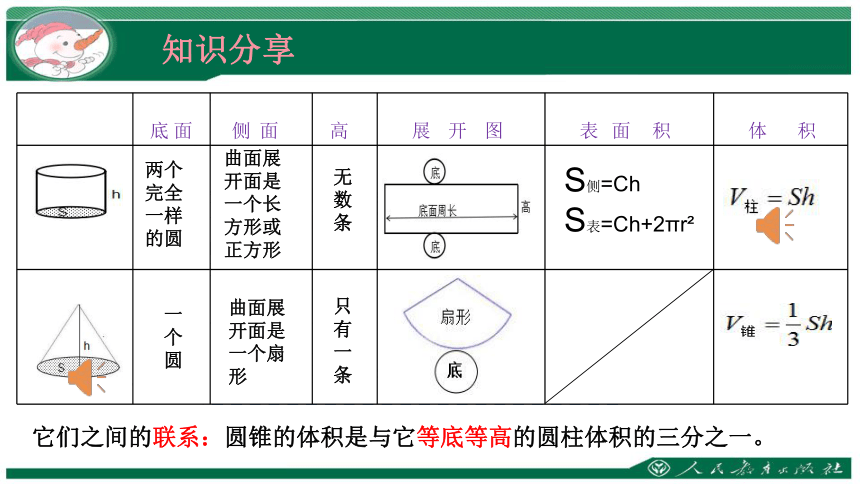
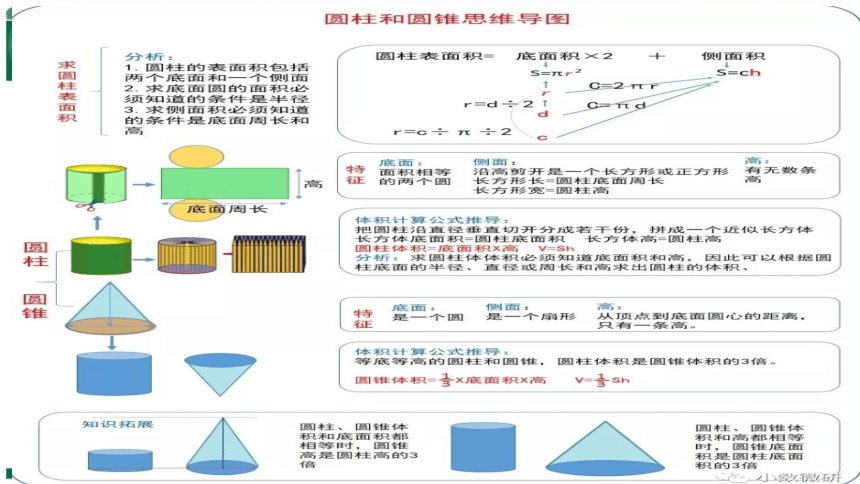
底 面 侧 面 高 展 开 图 表 面 积
体 积
两个完全一样的圆
一
个
圆
曲面展开面是一个长方形或正方形
曲面展开面是一个扇形
无数条
只有一条
它们之间的联系:圆锥的体积是与它等底等高的圆柱体积的三分之一。
S侧=Ch
S表=Ch+2πr
知识分享
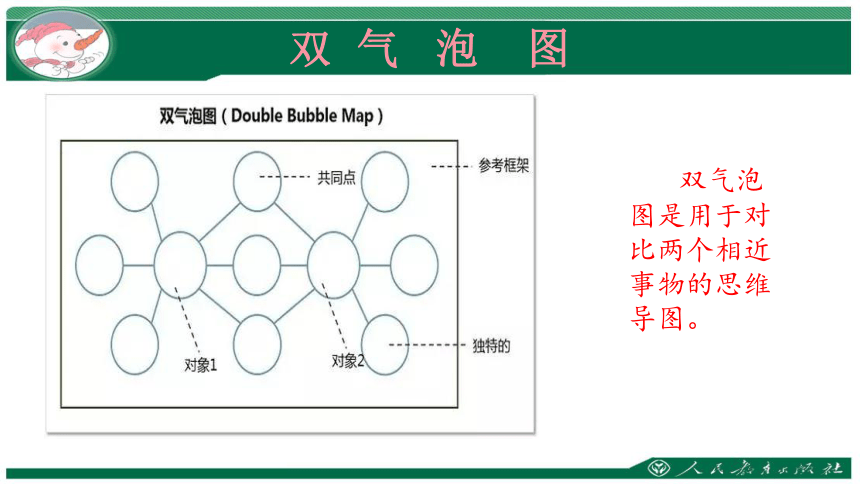
双 气 泡 图
双气泡图是用于对比两个相近事物的思维导图。
双 气 泡 图
双气泡图:圆柱与圆锥的对比
双气泡图:圆柱与圆锥的对比
......
......
......
圆柱两个底面之间的距离
叫做高。
O
O
高
h
r
从圆锥的顶点到底面圆心的距离是圆锥的高。
顶点
O
高
( )
( )
( )
( )
√
√
哪种方法测量圆柱与圆锥的高是正确的?
判 断:
圆柱的侧面沿高展开后是长方形
长方形的面积
圆柱的侧面积
=
长方形的长
底面的周长
宽
高
长×宽
=
底面周长×高
双气泡图:圆柱与圆锥的对比
......
......
......
底面
底面
侧面
底面
底面
圆柱的表面积
圆柱的侧面积+两个底面的面积
Ch+2πr
=
=
2πr h +2πr
πd h+2πr
=
=
S表
h
h
选 择
一个椰浆罐如右图
1.把这个椰浆罐放在桌面上,占多大的面积?是求这个罐子的( )。
2.给它的侧面全部贴上商标纸,至少需要多大的商标纸?
是求这个罐子的( )。
3.做这个罐子需要多少铁皮?( )。
4.这个椰浆罐最多能装多少椰浆?是求这个罐子的( )。
A、容积 B、体积 C、表面积 D、底面积 E、侧面积
D
E
C
A
圆柱的高不变,底面半径扩大到原来的2倍,体积就扩大到原来的2倍。( )
圆柱的底面半径扩大到原来的2倍,它的底面积就扩大到原来的 倍。高不变,根据公式V=Sh可知圆柱的体积应该扩大到原来的4倍。
×
双气泡图:圆柱与圆锥的对比
......
......
......
实验探究:准备好等底、等高的圆柱、圆锥形容器。
一个圆锥的底面直径是4dm,高是2dm,请计算这个 圆锥的体积。
3.14×(4÷2) ×2=25.12(dm )
答:这个圆锥的体积是25.12dm 。
出错了!
淘气混淆了圆柱和圆锥的体积公式,没有乘 。
正确答案:
×3.14×(4÷2) ×2≈8.37(dm )
答:这个圆锥的体积约是8.37dm 。
判 断
1.圆柱的体积比圆锥的体积大。 ( )
2.若一个圆锥的底面积是一个和它 的圆柱底面积
的3倍,则他们的体积相等。 ( )
3.把一个圆柱削成一个最大的圆锥,削掉的部分的体积
是圆锥体积的3倍。 ( )
4.一个圆柱和一个圆锥等底等高,它们的体积之和是
36dm ,那么这个圆锥的体积是12dm 。 ( )
×
等高
√
若一个圆锥的高是一个和它
等底面积的圆柱的高的3倍,
则它们的体积相等。
×
把一个圆柱削成一个最大的圆锥,削掉部分的体积是圆锥体积的2倍。
×
圆柱的体积:圆锥的体积=3:1,把36dm 的体积和四等分,圆锥体积占其中一份,应该是9dm 。
解题要领
确定形体,判断所求; 联系实际,运用公式;
关注单位,适时统一; 妙用π值,计算简便;
结合情境,进一去尾; 书写工整,合理布局。
1
妈妈给小雨的塑料水壶做一个布套(如图),小雨每天上学带一壶水。
(1)至少用了多少布料?
(2)小雨在学校一天喝1.5L水,这壶水够喝吗?(水壶的厚度忽略不计)
点 拨:
1.用多少布料求的是圆柱的表面积;
2.能装多少水是求圆柱的容积。
1
妈妈给小雨的塑料水壶做一个布套(如图),小雨每天上学带一壶水。
(1)至少用了多少布料?
(2)小雨在学校一天喝1.5L水,这壶水够喝吗?(水壶的厚度忽略不计)
拓展应用
点 拨:
1.用多少布料求的是圆柱的表面积;
2.能装多少水是求圆柱的容积;
3.已知单位和所求单位要进行换算。
(1)2×(10÷2) ×π+10×π×20
=50π+200π
=250π
=785 (cm )
答:至少用785 cm 布料。
(2)(10÷2) ×π×20
=25π×20
=1570(cm )
=1.57(dm )
=1.57( L )
1.57L>1.5L
答:这壶水够喝。
2
一种水稻磨米机的漏斗是由圆柱和圆锥两部分组成。底面直径是4dm,圆柱高2dm,圆锥高4dm。每立方分米稻谷重0.65kg。
(1)这个漏斗最多能装多少千克稻谷?
(2)如果稻谷的出米率是70%,一漏斗稻谷能磨多少大米?
拓展应用
点 拨:
1.这个漏斗是一个组合体,由等底不等高的圆柱和圆锥组合而成。
2.稻谷重量×出米率=大米重量
2
一种水稻磨米机的漏斗是由圆柱和圆锥两部分组成。底面直径是4dm,圆柱高2dm,圆锥高4dm。每立方分米稻谷重0.65kg。
(1)这个漏斗最多能装多少千克稻谷?
(2)如果稻谷的出米率是70%,一漏斗稻谷能磨多少大米?
拓展应用
点 拨:
1.这个漏斗是一个组合体,由等底不等高的圆柱和圆锥组合而成。
2.稻谷重量×出米率=大米重量
(1)V柱:(4÷2) ×π×2
=8π
=25.12(dm )
V锥: ×π×(4÷2) ×4≈16.75(dm )
V斗: 25.12+16.75=41.87(dm )
41.87×0.65=27.2155(千克)≈27.21(千克)
答:这个漏斗最多能装27.21千克稻谷。
(2)27.21×70%=19.047(千克)
答:一漏斗稻谷能磨19.047千克大米。
今日作业:
练习七
1—5题
1
把一块长方体钢坯铸造成一根直径为4dm的圆柱形钢筋,求钢筋的长度。
12.56dm
5dm
4dm
作 业
点 拨:
钢坯和钢筋等体,又已知圆柱的底面直径,可求出它的底面积。体积除以底面积可得高,即钢筋的长。
V长:12.56×5×4 h柱:251.2÷[π×(4÷2) ]
=12.56×20 =251.2÷4π
=251.2(dm ) =251.2÷12.56
=20(dm)
答:钢筋长20分米。
2
一个圆锥形沙堆,底面积是28.26m ,高是2.5m。用这堆沙子在10m宽的公路上铺2cm厚的路面,能铺多少米?
10m
2cm
作 业
点 拨:
1、求圆锥的体积一定不要忘记乘三分之一。
2、圆锥体沙堆与所铺长方体路面体积相等,已知长方体的宽和高,可以求出它的长,也就是铺的长度。
3、题中单位不统一,所以要想到统计单位后再计算。
2cm=0.02m
V锥: ×28.26×2.5
=9.42×2.5
=23.55(m )
长:23.55÷10÷0.02
=2.355÷0.02
=117.75(m)
答:能铺117.75米。
3
一块蜂窝煤如图所示。做一块蜂窝煤大约需要用煤多少立方分米?
作 业
点 拨:要注意单位换算;进一法取值
解题思路:
大圆柱体的体积 – 12个小圆柱体的体积=一块蜂窝煤的体积
(12÷2) ×π×9-(2÷2) ×π×9×12
=324π-108π
=216π
=678.24(cm )
=0.67824(dm )
≈0.68(dm )
答:大约需要用煤0.68立方分米。
4
有块正方体的木料,它的棱长是4dm。把这块木料加工成一个最大的圆柱(如图)。这个圆柱的体积是多少?
作 业
点 拨:
把正方体加工成一个最大的圆柱体,说明圆柱的底面直径和高都等于正方体的棱长。
(4÷2) ×π×4
=16π
=50.24(dm )
答:这个圆柱的体积是50.24立方分米。
5
一支120mL的牙膏管口直径5mm,李叔叔每天刷2次牙,每次挤出的牙膏长度是2cm。这支牙膏最多能用多少天?(得数保留整数)
作 业
点 拨:
1.单位要统一;2.最后结果用去尾法保留整数;3.每天刷两次。
5mm=0.5cm (0.5÷2) ×π×2×2
=0.0625×4π
=0.25×3.14
=0.785(cm )
120÷0.785≈152.866=152(天)
答:这支牙膏最多能用152天。
谢谢观看
整 理
复 习
梳理知识
形成网络
巩固旧知
提升记忆
突破难点
灵活运用
综合拓展
纠正错误
1
把一块长方体钢坯铸造成一根直径为4dm的圆柱形钢筋,求钢筋的长度。
12.56dm
5dm
4dm
作 业
点 拨:
钢坯和钢筋等体,又已知圆柱的底面直径,可求出它的底面积。体积除以底面积可得高,即钢筋的长。
2
一个圆锥形沙堆,底面积是28.26m ,高是2.5m。用这堆沙子在10m宽的公路上铺2cm厚的路面,能铺多少米
10m
2cm
作 业
点 拨:
1.求圆锥的体积一定不要忘记乘三分之一。
2.圆锥体沙堆与所铺长方体路面体积相等,已知长方体的宽和高,可以求出它的长,也就是铺的长度。
3.题中单位不统一,所以要想到统计单位后再计算。
3
一块蜂窝煤如图所示。做一块蜂窝煤大约需要用煤多少立方分米?
作 业
点 拨:
1.要注意单位换算;
2.进一法取值。
解题思路:
大圆柱体的体积 – 12个小圆柱体的体积=一块蜂窝煤的体积
《圆柱与圆锥》整理和复习
小学数学-人教版-六年级下册-第三单元
电子教材
整
理
复
习
圆柱与圆锥
形成网络
梳理知识
巩固旧知
提升记忆
突破难点
纠正错误
灵活运用
综合拓展
知识分享
在圆柱与圆锥单元,你有哪些收获呢?
我知道了圆柱是由两个底面和一个侧面组成的,底面是两个大小一样的圆。
我发现圆柱有无数条高,沿高线展开后的侧面是一个长方形或正方形。
圆柱的体积公式是 V= S h
我知道了圆柱的表面积就是侧面积与两个底面积的和。
知识分享
你们知道圆锥有什么特征吗?它与圆柱之间有什么区别与联系?
我知道圆锥的底面是一个圆,侧面是一个曲面。从圆锥的顶点到底面圆心的距离是圆锥的高。因此它只有一条高,而圆柱有无数条高。圆锥只有一个底面,圆柱有两个底面。
圆锥的体积是与它等底等高的圆柱的体积的三分之一。
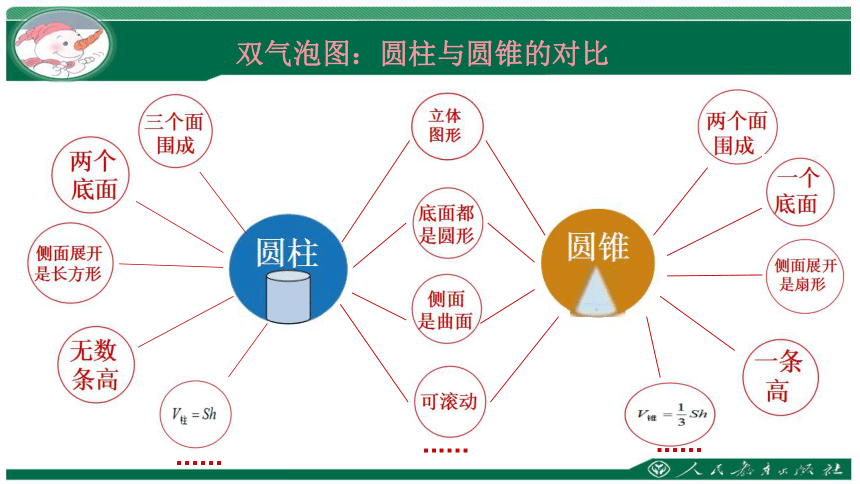
底 面 侧 面 高 展 开 图 表 面 积
体 积
两个完全一样的圆
一
个
圆
曲面展开面是一个长方形或正方形
曲面展开面是一个扇形
无数条
只有一条
它们之间的联系:圆锥的体积是与它等底等高的圆柱体积的三分之一。
S侧=Ch
S表=Ch+2πr
知识分享
双 气 泡 图
双气泡图是用于对比两个相近事物的思维导图。
双 气 泡 图
双气泡图:圆柱与圆锥的对比
双气泡图:圆柱与圆锥的对比
......
......
......
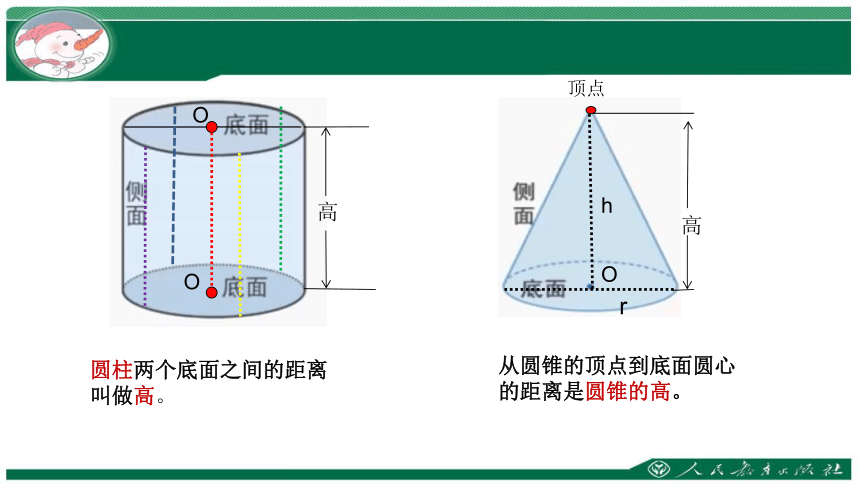
圆柱两个底面之间的距离
叫做高。
O
O
高
h
r
从圆锥的顶点到底面圆心的距离是圆锥的高。
顶点
O
高
( )
( )
( )
( )
√
√
哪种方法测量圆柱与圆锥的高是正确的?
判 断:
圆柱的侧面沿高展开后是长方形
长方形的面积
圆柱的侧面积
=
长方形的长
底面的周长
宽
高
长×宽
=
底面周长×高
双气泡图:圆柱与圆锥的对比
......
......
......
底面
底面
侧面
底面
底面
圆柱的表面积
圆柱的侧面积+两个底面的面积
Ch+2πr
=
=
2πr h +2πr
πd h+2πr
=
=
S表
h
h
选 择
一个椰浆罐如右图
1.把这个椰浆罐放在桌面上,占多大的面积?是求这个罐子的( )。
2.给它的侧面全部贴上商标纸,至少需要多大的商标纸?
是求这个罐子的( )。
3.做这个罐子需要多少铁皮?( )。
4.这个椰浆罐最多能装多少椰浆?是求这个罐子的( )。
A、容积 B、体积 C、表面积 D、底面积 E、侧面积
D
E
C
A
圆柱的高不变,底面半径扩大到原来的2倍,体积就扩大到原来的2倍。( )
圆柱的底面半径扩大到原来的2倍,它的底面积就扩大到原来的 倍。高不变,根据公式V=Sh可知圆柱的体积应该扩大到原来的4倍。
×
双气泡图:圆柱与圆锥的对比
......
......
......
实验探究:准备好等底、等高的圆柱、圆锥形容器。
一个圆锥的底面直径是4dm,高是2dm,请计算这个 圆锥的体积。
3.14×(4÷2) ×2=25.12(dm )
答:这个圆锥的体积是25.12dm 。
出错了!
淘气混淆了圆柱和圆锥的体积公式,没有乘 。
正确答案:
×3.14×(4÷2) ×2≈8.37(dm )
答:这个圆锥的体积约是8.37dm 。
判 断
1.圆柱的体积比圆锥的体积大。 ( )
2.若一个圆锥的底面积是一个和它 的圆柱底面积
的3倍,则他们的体积相等。 ( )
3.把一个圆柱削成一个最大的圆锥,削掉的部分的体积
是圆锥体积的3倍。 ( )
4.一个圆柱和一个圆锥等底等高,它们的体积之和是
36dm ,那么这个圆锥的体积是12dm 。 ( )
×
等高
√
若一个圆锥的高是一个和它
等底面积的圆柱的高的3倍,
则它们的体积相等。
×
把一个圆柱削成一个最大的圆锥,削掉部分的体积是圆锥体积的2倍。
×
圆柱的体积:圆锥的体积=3:1,把36dm 的体积和四等分,圆锥体积占其中一份,应该是9dm 。
解题要领
确定形体,判断所求; 联系实际,运用公式;
关注单位,适时统一; 妙用π值,计算简便;
结合情境,进一去尾; 书写工整,合理布局。
1
妈妈给小雨的塑料水壶做一个布套(如图),小雨每天上学带一壶水。
(1)至少用了多少布料?
(2)小雨在学校一天喝1.5L水,这壶水够喝吗?(水壶的厚度忽略不计)
点 拨:
1.用多少布料求的是圆柱的表面积;
2.能装多少水是求圆柱的容积。
1
妈妈给小雨的塑料水壶做一个布套(如图),小雨每天上学带一壶水。
(1)至少用了多少布料?
(2)小雨在学校一天喝1.5L水,这壶水够喝吗?(水壶的厚度忽略不计)
拓展应用
点 拨:
1.用多少布料求的是圆柱的表面积;
2.能装多少水是求圆柱的容积;
3.已知单位和所求单位要进行换算。
(1)2×(10÷2) ×π+10×π×20
=50π+200π
=250π
=785 (cm )
答:至少用785 cm 布料。
(2)(10÷2) ×π×20
=25π×20
=1570(cm )
=1.57(dm )
=1.57( L )
1.57L>1.5L
答:这壶水够喝。
2
一种水稻磨米机的漏斗是由圆柱和圆锥两部分组成。底面直径是4dm,圆柱高2dm,圆锥高4dm。每立方分米稻谷重0.65kg。
(1)这个漏斗最多能装多少千克稻谷?
(2)如果稻谷的出米率是70%,一漏斗稻谷能磨多少大米?
拓展应用
点 拨:
1.这个漏斗是一个组合体,由等底不等高的圆柱和圆锥组合而成。
2.稻谷重量×出米率=大米重量
2
一种水稻磨米机的漏斗是由圆柱和圆锥两部分组成。底面直径是4dm,圆柱高2dm,圆锥高4dm。每立方分米稻谷重0.65kg。
(1)这个漏斗最多能装多少千克稻谷?
(2)如果稻谷的出米率是70%,一漏斗稻谷能磨多少大米?
拓展应用
点 拨:
1.这个漏斗是一个组合体,由等底不等高的圆柱和圆锥组合而成。
2.稻谷重量×出米率=大米重量
(1)V柱:(4÷2) ×π×2
=8π
=25.12(dm )
V锥: ×π×(4÷2) ×4≈16.75(dm )
V斗: 25.12+16.75=41.87(dm )
41.87×0.65=27.2155(千克)≈27.21(千克)
答:这个漏斗最多能装27.21千克稻谷。
(2)27.21×70%=19.047(千克)
答:一漏斗稻谷能磨19.047千克大米。
今日作业:
练习七
1—5题
1
把一块长方体钢坯铸造成一根直径为4dm的圆柱形钢筋,求钢筋的长度。
12.56dm
5dm
4dm
作 业
点 拨:
钢坯和钢筋等体,又已知圆柱的底面直径,可求出它的底面积。体积除以底面积可得高,即钢筋的长。
V长:12.56×5×4 h柱:251.2÷[π×(4÷2) ]
=12.56×20 =251.2÷4π
=251.2(dm ) =251.2÷12.56
=20(dm)
答:钢筋长20分米。
2
一个圆锥形沙堆,底面积是28.26m ,高是2.5m。用这堆沙子在10m宽的公路上铺2cm厚的路面,能铺多少米?
10m
2cm
作 业
点 拨:
1、求圆锥的体积一定不要忘记乘三分之一。
2、圆锥体沙堆与所铺长方体路面体积相等,已知长方体的宽和高,可以求出它的长,也就是铺的长度。
3、题中单位不统一,所以要想到统计单位后再计算。
2cm=0.02m
V锥: ×28.26×2.5
=9.42×2.5
=23.55(m )
长:23.55÷10÷0.02
=2.355÷0.02
=117.75(m)
答:能铺117.75米。
3
一块蜂窝煤如图所示。做一块蜂窝煤大约需要用煤多少立方分米?
作 业
点 拨:要注意单位换算;进一法取值
解题思路:
大圆柱体的体积 – 12个小圆柱体的体积=一块蜂窝煤的体积
(12÷2) ×π×9-(2÷2) ×π×9×12
=324π-108π
=216π
=678.24(cm )
=0.67824(dm )
≈0.68(dm )
答:大约需要用煤0.68立方分米。
4
有块正方体的木料,它的棱长是4dm。把这块木料加工成一个最大的圆柱(如图)。这个圆柱的体积是多少?
作 业
点 拨:
把正方体加工成一个最大的圆柱体,说明圆柱的底面直径和高都等于正方体的棱长。
(4÷2) ×π×4
=16π
=50.24(dm )
答:这个圆柱的体积是50.24立方分米。
5
一支120mL的牙膏管口直径5mm,李叔叔每天刷2次牙,每次挤出的牙膏长度是2cm。这支牙膏最多能用多少天?(得数保留整数)
作 业
点 拨:
1.单位要统一;2.最后结果用去尾法保留整数;3.每天刷两次。
5mm=0.5cm (0.5÷2) ×π×2×2
=0.0625×4π
=0.25×3.14
=0.785(cm )
120÷0.785≈152.866=152(天)
答:这支牙膏最多能用152天。
谢谢观看
整 理
复 习
梳理知识
形成网络
巩固旧知
提升记忆
突破难点
灵活运用
综合拓展
纠正错误
1
把一块长方体钢坯铸造成一根直径为4dm的圆柱形钢筋,求钢筋的长度。
12.56dm
5dm
4dm
作 业
点 拨:
钢坯和钢筋等体,又已知圆柱的底面直径,可求出它的底面积。体积除以底面积可得高,即钢筋的长。
2
一个圆锥形沙堆,底面积是28.26m ,高是2.5m。用这堆沙子在10m宽的公路上铺2cm厚的路面,能铺多少米
10m
2cm
作 业
点 拨:
1.求圆锥的体积一定不要忘记乘三分之一。
2.圆锥体沙堆与所铺长方体路面体积相等,已知长方体的宽和高,可以求出它的长,也就是铺的长度。
3.题中单位不统一,所以要想到统计单位后再计算。
3
一块蜂窝煤如图所示。做一块蜂窝煤大约需要用煤多少立方分米?
作 业
点 拨:
1.要注意单位换算;
2.进一法取值。
解题思路:
大圆柱体的体积 – 12个小圆柱体的体积=一块蜂窝煤的体积
