第六章 第2节 密度(人教版物理八年级上册课件)(共26张PPT)
文档属性
| 名称 | 第六章 第2节 密度(人教版物理八年级上册课件)(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 29.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-07-21 19:02:34 | ||
图片预览








文档简介
(共26张PPT)
第2节 密度
一个古老的故事:
古时候,在地中海上,有一个叙拉古王国,它的国王交给金匠一定质量的黄金,让金匠为自己打造一顶纯金的王冠,当王冠打造完毕交给国王时,国王发现这个金冠精美无比,但国王却怀疑金匠偷窃了他的黄金而用其它便宜的金属偷梁换柱。
国王令人用秤去称,结果王冠的质量与国王交给金匠的黄金的质量是相同的。
1.如何去鉴别王冠是否是纯金制成的?
2.抗洪抢险的战士穿的救生衣的材料是什么?
3.配制鸡尾酒,为什么可以区分出美丽的颜色和层次?
4.气球中为什么要充有氢气、氦气或热空气?
1.铁块、铝块和铜块,如何来区分它们?
2.用纸把体积相同的铁块、铝块和分别包起来,那如何来分辨它们呢?
3.质量相同的铁块和铝块,你又如何来区分它们?
4.若质量和体积都不相同的铁块和铝块,你又如何来区分它们?
观察及思考:
器材:
托盘天平
砝码
体积相同的铜块、铁块、铝块
实验一:用天平测量具有相同体积的不同物质的质量。(体积已知)
一、实验探究
将实验测量数据填入下表中:
质量 /kg 体积 /cm3
铁块 10
铜块 10
铝块 10
结论:体积相同的不同物质质量不同。
79
27
89
结论:质量相同的不同物质体积不同。
实验二:
用天平比较质量相同的不同物质的体积
质量/g 体积/cm3 质量/体积(g/cm3)
木块1 10
木块2 20
木块3 30
5
10
15
0.5
0.5
0.5
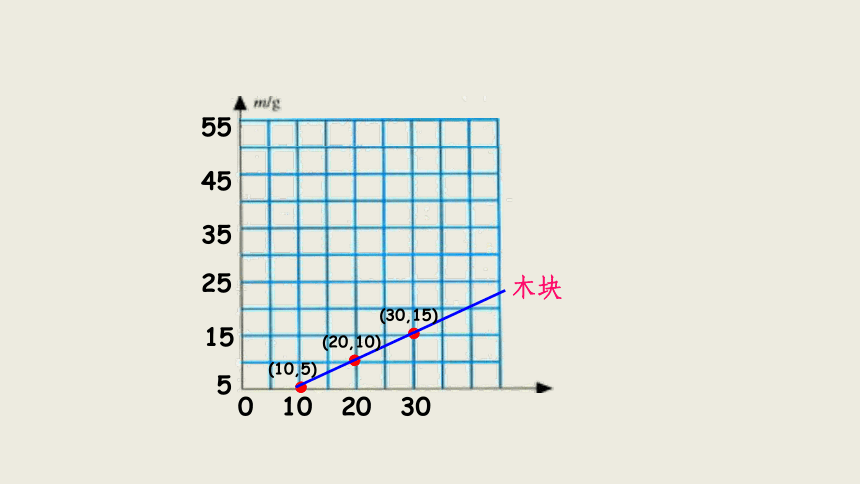
实验三:探究同种物质的质量和体积的关系
10cm3
20cm3
30cm3
10
20
30
0
55
45
35
25
15
5
木块
(10,5)
(20,10)
(30,15)
质量/g 体积/cm3 质量/体积 (g/cm3)
铝块1 10
铝块2 20
铝块3 30
27
54
81
2.7
2.7
2.7
10cm3
20cm3
30cm3
10
20
30
0
55
45
35
25
15
5
铝块
(10,27)
(20,54)
通过所作的图象,你得到什么结论?
10
20
30
0
55
45
35
25
15
5
木块
铝块
(10,27)
(20,54)
(10,5)
(20,10)
(30,15)
分析和论证
实验证明:
同种物质的质量和体积之间的比值是一定的.
不同物质的质量与体积之间的比值是不同的。
因此,这个比值反映了物质的一种特性。
为了描述物质的这种特性我们引入了
——密度的概念
1.定义:某种物质组成物体的质量与它的体积之 比叫做这种物质的密度
二、密度
2.物理意义:
3.计算公式:
4.单 位:
质量
体积
表示物质特性的物理量
千克/米3
克/厘米3
国际单位:
常用单位:
)
)
密度=
(
(
Kg/m
3
g/cm
3
1g/cm3 =1×
10-6m3
10-3kg
= 103kg/m3
即:
=
1 g/cm
1000kg/m3
3
1 kg/m3
=
g/cm3
1×10-3
5、单位换算
观察表中数据能发现一些规律吗?
三、密度表
1.一般:ρ固>ρ液>ρ气
2.一些物质密度相同:如冰和蜡,酒精和煤油;
3.同种物质物态不同密度可能不同:如冰和水
4.固体和液体密度用国际单位,数值都表示
为“×103 ”的形式,如ρ水=1.0×103 kg/m3 ;
气体密度用国际单位,数值没有“×103”,
如ρ空气=1.29 kg/m3
1.一定状态下同种物质,密度不随质量和体积变化;
2.不同种物质,密度一般不同。
四、密度是反映物质特性的物理量
密度公式的应用:
1.计算物质的密度: ρ=m/V
计算密度.鉴别物质
2.计算物体的体积: V=m/ ρ
可以计算一些体积难以测量的物体
(如沙子、等一些形状不规则的物体)
3.计算物体的质量: m=ρV
有些物体的质量太大不便于直接测量
1.计算物质的密度: ρ=m/V
例:有一枚第十一届亚运会纪念币,它的质量为16 .1克,体积为1 .8厘米3,试求制成这枚纪念币的金属密度,是何种金属?
计算密度.鉴别物质
一个金属零件的体积为400dm3,质量为1080Kg,那么该零件的密度为多少?它可能是什么金属?
2.计算物体的体积: V=m/ ρ
例:用天平称得一捆细铜丝的质量是445克,已知铜的密度是8.9×103千克/米3,这捆细铜丝的体积是多少?
可以计算一些体积难以测量的物体
(如沙子、等一些形状不规则的物体)
注:如果知道铜丝的横截面积还可以计算出这捆铜丝的长度。
3.计算物体的质量: m=ρV
例:人民英雄纪念碑的碑心石是体积为42.6米3的一整块花岗岩,花岗岩的密度是2.6×103千克/米3,碑心石的质量是多少?
可以计算质量难以测量的物体
(如金字塔、人民英雄纪念碑等)
1、根据密度公式ρ=m/V,下列说法中正确的是( )
A.物体的密度与物体的质量成正比
B.物体的密度与物体的体积成反比
C.物体的密度与质量成正比同时与体积成反比
D.密度是物质的一种特性与质量、体积无关
D
当堂检测
2、一个铅球用了多年,没有发生改变的是( )
A.质量 B.体积
C.密度 D.三者都没改变
C
3、判断一下:
1、大铝块的质量为4㎏,小铝块的质量为1㎏,则大铝块的密度大于小铝块的密度。 ( )
2、一杯酒精用去一半后,剩下的酒精密度为原来的一半。( )
4、填空
甲、乙两物体的质量之比3:2,体积之比2:3则甲、乙两物体的密度之比为____,若把甲物体截去1/2,乙物体截去1/3则剩下的甲、乙两物体的密度之比为____。
9:4
×
×
9:4
谢 谢
第2节 密度
一个古老的故事:
古时候,在地中海上,有一个叙拉古王国,它的国王交给金匠一定质量的黄金,让金匠为自己打造一顶纯金的王冠,当王冠打造完毕交给国王时,国王发现这个金冠精美无比,但国王却怀疑金匠偷窃了他的黄金而用其它便宜的金属偷梁换柱。
国王令人用秤去称,结果王冠的质量与国王交给金匠的黄金的质量是相同的。
1.如何去鉴别王冠是否是纯金制成的?
2.抗洪抢险的战士穿的救生衣的材料是什么?
3.配制鸡尾酒,为什么可以区分出美丽的颜色和层次?
4.气球中为什么要充有氢气、氦气或热空气?
1.铁块、铝块和铜块,如何来区分它们?
2.用纸把体积相同的铁块、铝块和分别包起来,那如何来分辨它们呢?
3.质量相同的铁块和铝块,你又如何来区分它们?
4.若质量和体积都不相同的铁块和铝块,你又如何来区分它们?
观察及思考:
器材:
托盘天平
砝码
体积相同的铜块、铁块、铝块
实验一:用天平测量具有相同体积的不同物质的质量。(体积已知)
一、实验探究
将实验测量数据填入下表中:
质量 /kg 体积 /cm3
铁块 10
铜块 10
铝块 10
结论:体积相同的不同物质质量不同。
79
27
89
结论:质量相同的不同物质体积不同。
实验二:
用天平比较质量相同的不同物质的体积
质量/g 体积/cm3 质量/体积(g/cm3)
木块1 10
木块2 20
木块3 30
5
10
15
0.5
0.5
0.5
实验三:探究同种物质的质量和体积的关系
10cm3
20cm3
30cm3
10
20
30
0
55
45
35
25
15
5
木块
(10,5)
(20,10)
(30,15)
质量/g 体积/cm3 质量/体积 (g/cm3)
铝块1 10
铝块2 20
铝块3 30
27
54
81
2.7
2.7
2.7
10cm3
20cm3
30cm3
10
20
30
0
55
45
35
25
15
5
铝块
(10,27)
(20,54)
通过所作的图象,你得到什么结论?
10
20
30
0
55
45
35
25
15
5
木块
铝块
(10,27)
(20,54)
(10,5)
(20,10)
(30,15)
分析和论证
实验证明:
同种物质的质量和体积之间的比值是一定的.
不同物质的质量与体积之间的比值是不同的。
因此,这个比值反映了物质的一种特性。
为了描述物质的这种特性我们引入了
——密度的概念
1.定义:某种物质组成物体的质量与它的体积之 比叫做这种物质的密度
二、密度
2.物理意义:
3.计算公式:
4.单 位:
质量
体积
表示物质特性的物理量
千克/米3
克/厘米3
国际单位:
常用单位:
)
)
密度=
(
(
Kg/m
3
g/cm
3
1g/cm3 =1×
10-6m3
10-3kg
= 103kg/m3
即:
=
1 g/cm
1000kg/m3
3
1 kg/m3
=
g/cm3
1×10-3
5、单位换算
观察表中数据能发现一些规律吗?
三、密度表
1.一般:ρ固>ρ液>ρ气
2.一些物质密度相同:如冰和蜡,酒精和煤油;
3.同种物质物态不同密度可能不同:如冰和水
4.固体和液体密度用国际单位,数值都表示
为“×103 ”的形式,如ρ水=1.0×103 kg/m3 ;
气体密度用国际单位,数值没有“×103”,
如ρ空气=1.29 kg/m3
1.一定状态下同种物质,密度不随质量和体积变化;
2.不同种物质,密度一般不同。
四、密度是反映物质特性的物理量
密度公式的应用:
1.计算物质的密度: ρ=m/V
计算密度.鉴别物质
2.计算物体的体积: V=m/ ρ
可以计算一些体积难以测量的物体
(如沙子、等一些形状不规则的物体)
3.计算物体的质量: m=ρV
有些物体的质量太大不便于直接测量
1.计算物质的密度: ρ=m/V
例:有一枚第十一届亚运会纪念币,它的质量为16 .1克,体积为1 .8厘米3,试求制成这枚纪念币的金属密度,是何种金属?
计算密度.鉴别物质
一个金属零件的体积为400dm3,质量为1080Kg,那么该零件的密度为多少?它可能是什么金属?
2.计算物体的体积: V=m/ ρ
例:用天平称得一捆细铜丝的质量是445克,已知铜的密度是8.9×103千克/米3,这捆细铜丝的体积是多少?
可以计算一些体积难以测量的物体
(如沙子、等一些形状不规则的物体)
注:如果知道铜丝的横截面积还可以计算出这捆铜丝的长度。
3.计算物体的质量: m=ρV
例:人民英雄纪念碑的碑心石是体积为42.6米3的一整块花岗岩,花岗岩的密度是2.6×103千克/米3,碑心石的质量是多少?
可以计算质量难以测量的物体
(如金字塔、人民英雄纪念碑等)
1、根据密度公式ρ=m/V,下列说法中正确的是( )
A.物体的密度与物体的质量成正比
B.物体的密度与物体的体积成反比
C.物体的密度与质量成正比同时与体积成反比
D.密度是物质的一种特性与质量、体积无关
D
当堂检测
2、一个铅球用了多年,没有发生改变的是( )
A.质量 B.体积
C.密度 D.三者都没改变
C
3、判断一下:
1、大铝块的质量为4㎏,小铝块的质量为1㎏,则大铝块的密度大于小铝块的密度。 ( )
2、一杯酒精用去一半后,剩下的酒精密度为原来的一半。( )
4、填空
甲、乙两物体的质量之比3:2,体积之比2:3则甲、乙两物体的密度之比为____,若把甲物体截去1/2,乙物体截去1/3则剩下的甲、乙两物体的密度之比为____。
9:4
×
×
9:4
谢 谢
同课章节目录
- 科学之旅
- 第一章 机械运动
- 第1节 长度和时间的测量
- 第2节 运动的描述
- 第3节 运动的快慢
- 第4节 测量平均速度
- 第二章 声现象
- 第1节 声音的产生和传播
- 第2节 声音的特性
- 第3节 声的利用
- 第4节 噪声的危害和控制
- 第三章 物态变化
- 第1节 温度
- 第2节 熔化和凝固
- 第3节 汽化和液化
- 第4节 升华和凝华
- 第四章 光现象
- 第1节 光的直线传播
- 第2节 光的反射
- 第3节 平面镜成像
- 第4节 光的折射
- 第5节 光的色散
- 第五章 透镜及其应用
- 第1节 透镜
- 第2节 生活中的透镜
- 第3节 凸透镜成像的规律
- 第4节 眼睛和眼镜
- 第5节 显微镜和望远镜
- 第六章 质量和密度
- 第1节 质量
- 第2节 密度
- 第3节 测量物质的密度
- 第4节 密度与社会生活
