人教版八年级下册19.2.2一次函数 课件(共24张PPT)
文档属性
| 名称 | 人教版八年级下册19.2.2一次函数 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-22 08:08:50 | ||
图片预览








文档简介
(共24张PPT)
课程:数学
《 一次函数的概念》
人教版
八年级下册 第5课时
第 19 章 一次函数
教学目标
1
2
3
知识与技能
理解一次函数和正比例函数的概念并能结合具体情境理解一次函数的意义,根据实际问题中的数量关系写出一次函数的解析式。
过程与方法
经历由实际问题引出一次函数解析式的过程,体会数学与现实生活的联系。
情感态度和价值观
培养学生探究,合作学习的习惯,并在运用数学知识解答问题的活动中获取成功的体验,建立学习的自信心。
目录
CONTENTS
01
新课导入
New class introduction
02
探究新知
Explore new knowledge
03
课堂练习
class exercise
04
课堂小结
Class summary
01
PART ONE
新课导入
New class introduction
新课导入
k>0
k<0
x
y
0
x
y
0
一、三象限
二、四象限
y随x的增大而减小
y随x的增大而增大
图像必经过(0,0)和(1,k)这两个点
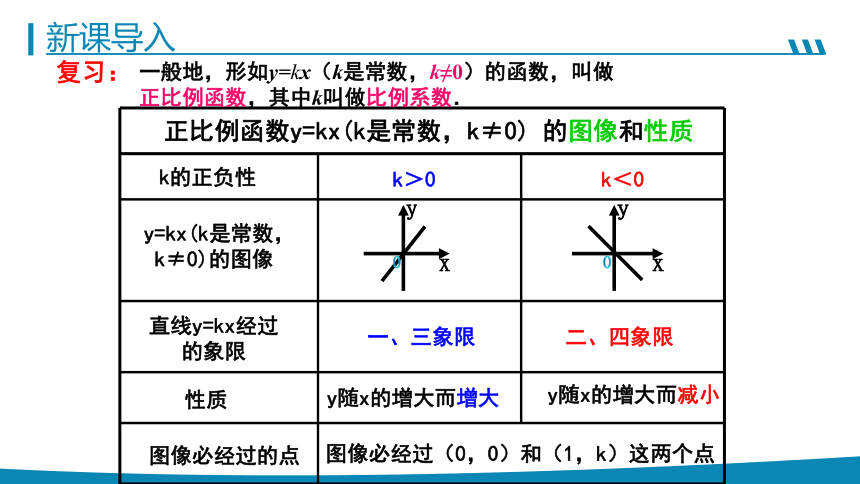
正比例函数y=kx(k是常数,k≠0) 的图像和性质
k的正负性
y=kx(k是常数,
k≠0)的图像
直线y=kx经过
的象限
性质
图像必经过的点
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
复习:
02
PART TWO
探究新知
Explore new knowledge
探究新知
问题与探究
某登山队大本营所在地的气温为5℃,海拔每升高1km气温下降6℃ ,登山队员由大本营向上登高xkm时,他们所在位置的气温是y℃.
(1)试用解析式表示y与x的关系.
解:y与x的函数关系式为
y=5-6x
这个函数关系式也可以写为
y=-6x+5
(2)当登山队员由大本营向上登高0.5km时他们所在位置的气温是多少?
解:当x=0.5时,y=-6×0.5+5=2℃
探究新知
讨论与思考
下列问题中的变量对应关系可用怎样的函数表示?
(1)有人发现,在20-25 ℃的蟋蟀每分钟名叫次数c与温度t(单位:℃ )有关即c的值约是t的七倍与35的差;
解: c=7t-35
(2)一种计算成年人标准体重G(单位:千克)的方法是,以厘米为单位量出身高值h减常数105,所得差是G的值;
解:G=h-105
探究新知
(3)某城市的市内电话的月收费额y(单位:元)包括:月租费22元,拨打电话x分钟的计时费按0.01元/分钟收取;
解:y=0.01x+22
(4)把一个长10cm、宽5cm的长方形的长减少xcm,宽不变,长方形的面积y(单位:cm2)随x的值而变化.
解:y=-5x+50
探究新知
观察与发现
认真观察以上出现的四个函数解析式,分别说出哪些是常数、自变量和函数.
函数解析式 常数 自变量 函数
(1)c=7t-35 (2)G=h-105 (3)y=0.01x+22 (4)y=-5x+50 这些函数有什么共同点?
这些函数都是常数和自变量的乘积与另一个常数的和的形式!
7,-35
t
c
1,-105
h
G
0.01,22
x
y
-5,50
x
y
探究新知
函数解析式 常数 自变量 函数
(1)c=7t-35 (2)G=h-105 (3)y=0.01x+22 (4)y=-5x+50 这些函数有什么共同点?
这些函数都是常数和自变量的乘积与一个常数的和的形式!
7,-35
t
c
1,-105
h
G
0.01,22
x
y
-5,50
x
y
函数解析式 常数 自变量 函数
(1)l=2πr (2)m=7.8V (3)h=0.5n (4)T= -2t 2π
r
l
7.8
V
m
0.5
n
h
-2
t
T
这些函数有什么共同点?
这些函数都是常数与自变量的乘积的形式!
正比例函数
一次函数
探究新知
归纳与总结
一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数.当b=0时, y=kx+b即y=kx,所以说正比例函数是一种特殊的一次函数.
做一做:判断下列函数是否是一次函数?如果是,k、b分别是多少
y=2x
y=-0.5x+1
y=2x2+1
2
x
y=
-5
y=
x
3
+1
2
x2
y=
-5
3
πx
y=
这里为什么强调k、b是常数, k≠0呢?
你能举出一些一次函数的例子吗?
探究新知
例1 已知y与x-3成正比例,当x=4时,y=3.
(1)写出y与x之间的函数关系式;
(2)y与x之间是什么函数关系;
(3)求x=2.5时,y的值.
探究新知
y=3x-9
(2) y是x的一次函数.
y=3×2.5 - 9= -1.5.
解:(1)设y=k(x-3)
把 x=4,y=3 代入上式,得 3= k(4-3)
解得 k=3
(3) 当x=2.5时
PART THREE
课堂练习
class exercise
03
探究新知
1.下列说法正确的是( )
A.一次函数是正比例函数
B.正比例函数不是一次函数
C.不是正比例函数就不是一次函数
D.正比例函数是一次函数
D
探究新知
2.有下列函数:①y=πx,②y=2x-1,③y= ,
④y= -3x,⑤y=x3-1,⑥y=3(2x2-2x)-6x2,
其中是一次函数的有( )
A.4个 B.3个 C.2个 D.1个
B
探究新知
3. 一个正方形的边长为3 cm,它的各边边长减少x cm后,得到的新正方形的周长为y cm,y与x之间的函数解析式是( )
A.y=12-4x B.y=4x-12
C.y=12-x D.以上都不对
A
探究新知
4.函数y=5x-3和y=5-3x都是形如y=kx+b的一次函数.在第一个式子中,k=_____,b=______;在第二个式子中,k=______,b=______.
5.已知函数y=(k-2)x+2k+2,当k____时,它是正比例函数;当k____时,它是一次函数.
5
-3
-3
5
=-1
≠2
探究新知
6.一次函数y=kx+b,当x=1时,y=5;
当x=-1时,y=1. 求k和b的值.
解:把 和 分别代入y=kx+b,
得 解得
所以k的值为2,b的值为3.
课堂练习
7. 已知函数 y=(m-1)x+1-m2.
(1)当m为何值时,这个函数是一次函数
(2)当m为何值时,这个函数是正比例函数
解:(1)由题意可得
m-1≠0,解得m≠1.
即m≠1时,这个函数是一次函数.
(2)由题意可得
m-1≠0,1-m2=0,解得m=-1.
即m=-1时,这个函数是正比例函数.
PART FOUR
课堂小结
Class summary
04
课堂小结
这节课你们都学会了哪些知识?
1、当两个一次函数的k一样,而b不一样,则这两个函数的图象是两条互相平行的直线,且它们之间可以通过平移得到(向上或向下),平移的距离是|b|。
2、当两个一次函数的b一样,而k不一样,则这两个函数的图象是两条相交的直线,且与y轴交于同一点,即(0,b)
Thank you!
人教版
八年级下册
第 19 章 一次函数
课程:数学
《 一次函数的概念》
人教版
八年级下册 第5课时
第 19 章 一次函数
教学目标
1
2
3
知识与技能
理解一次函数和正比例函数的概念并能结合具体情境理解一次函数的意义,根据实际问题中的数量关系写出一次函数的解析式。
过程与方法
经历由实际问题引出一次函数解析式的过程,体会数学与现实生活的联系。
情感态度和价值观
培养学生探究,合作学习的习惯,并在运用数学知识解答问题的活动中获取成功的体验,建立学习的自信心。
目录
CONTENTS
01
新课导入
New class introduction
02
探究新知
Explore new knowledge
03
课堂练习
class exercise
04
课堂小结
Class summary
01
PART ONE
新课导入
New class introduction
新课导入
k>0
k<0
x
y
0
x
y
0
一、三象限
二、四象限
y随x的增大而减小
y随x的增大而增大
图像必经过(0,0)和(1,k)这两个点
正比例函数y=kx(k是常数,k≠0) 的图像和性质
k的正负性
y=kx(k是常数,
k≠0)的图像
直线y=kx经过
的象限
性质
图像必经过的点
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
复习:
02
PART TWO
探究新知
Explore new knowledge
探究新知
问题与探究
某登山队大本营所在地的气温为5℃,海拔每升高1km气温下降6℃ ,登山队员由大本营向上登高xkm时,他们所在位置的气温是y℃.
(1)试用解析式表示y与x的关系.
解:y与x的函数关系式为
y=5-6x
这个函数关系式也可以写为
y=-6x+5
(2)当登山队员由大本营向上登高0.5km时他们所在位置的气温是多少?
解:当x=0.5时,y=-6×0.5+5=2℃
探究新知
讨论与思考
下列问题中的变量对应关系可用怎样的函数表示?
(1)有人发现,在20-25 ℃的蟋蟀每分钟名叫次数c与温度t(单位:℃ )有关即c的值约是t的七倍与35的差;
解: c=7t-35
(2)一种计算成年人标准体重G(单位:千克)的方法是,以厘米为单位量出身高值h减常数105,所得差是G的值;
解:G=h-105
探究新知
(3)某城市的市内电话的月收费额y(单位:元)包括:月租费22元,拨打电话x分钟的计时费按0.01元/分钟收取;
解:y=0.01x+22
(4)把一个长10cm、宽5cm的长方形的长减少xcm,宽不变,长方形的面积y(单位:cm2)随x的值而变化.
解:y=-5x+50
探究新知
观察与发现
认真观察以上出现的四个函数解析式,分别说出哪些是常数、自变量和函数.
函数解析式 常数 自变量 函数
(1)c=7t-35 (2)G=h-105 (3)y=0.01x+22 (4)y=-5x+50 这些函数有什么共同点?
这些函数都是常数和自变量的乘积与另一个常数的和的形式!
7,-35
t
c
1,-105
h
G
0.01,22
x
y
-5,50
x
y
探究新知
函数解析式 常数 自变量 函数
(1)c=7t-35 (2)G=h-105 (3)y=0.01x+22 (4)y=-5x+50 这些函数有什么共同点?
这些函数都是常数和自变量的乘积与一个常数的和的形式!
7,-35
t
c
1,-105
h
G
0.01,22
x
y
-5,50
x
y
函数解析式 常数 自变量 函数
(1)l=2πr (2)m=7.8V (3)h=0.5n (4)T= -2t 2π
r
l
7.8
V
m
0.5
n
h
-2
t
T
这些函数有什么共同点?
这些函数都是常数与自变量的乘积的形式!
正比例函数
一次函数
探究新知
归纳与总结
一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数.当b=0时, y=kx+b即y=kx,所以说正比例函数是一种特殊的一次函数.
做一做:判断下列函数是否是一次函数?如果是,k、b分别是多少
y=2x
y=-0.5x+1
y=2x2+1
2
x
y=
-5
y=
x
3
+1
2
x2
y=
-5
3
πx
y=
这里为什么强调k、b是常数, k≠0呢?
你能举出一些一次函数的例子吗?
探究新知
例1 已知y与x-3成正比例,当x=4时,y=3.
(1)写出y与x之间的函数关系式;
(2)y与x之间是什么函数关系;
(3)求x=2.5时,y的值.
探究新知
y=3x-9
(2) y是x的一次函数.
y=3×2.5 - 9= -1.5.
解:(1)设y=k(x-3)
把 x=4,y=3 代入上式,得 3= k(4-3)
解得 k=3
(3) 当x=2.5时
PART THREE
课堂练习
class exercise
03
探究新知
1.下列说法正确的是( )
A.一次函数是正比例函数
B.正比例函数不是一次函数
C.不是正比例函数就不是一次函数
D.正比例函数是一次函数
D
探究新知
2.有下列函数:①y=πx,②y=2x-1,③y= ,
④y= -3x,⑤y=x3-1,⑥y=3(2x2-2x)-6x2,
其中是一次函数的有( )
A.4个 B.3个 C.2个 D.1个
B
探究新知
3. 一个正方形的边长为3 cm,它的各边边长减少x cm后,得到的新正方形的周长为y cm,y与x之间的函数解析式是( )
A.y=12-4x B.y=4x-12
C.y=12-x D.以上都不对
A
探究新知
4.函数y=5x-3和y=5-3x都是形如y=kx+b的一次函数.在第一个式子中,k=_____,b=______;在第二个式子中,k=______,b=______.
5.已知函数y=(k-2)x+2k+2,当k____时,它是正比例函数;当k____时,它是一次函数.
5
-3
-3
5
=-1
≠2
探究新知
6.一次函数y=kx+b,当x=1时,y=5;
当x=-1时,y=1. 求k和b的值.
解:把 和 分别代入y=kx+b,
得 解得
所以k的值为2,b的值为3.
课堂练习
7. 已知函数 y=(m-1)x+1-m2.
(1)当m为何值时,这个函数是一次函数
(2)当m为何值时,这个函数是正比例函数
解:(1)由题意可得
m-1≠0,解得m≠1.
即m≠1时,这个函数是一次函数.
(2)由题意可得
m-1≠0,1-m2=0,解得m=-1.
即m=-1时,这个函数是正比例函数.
PART FOUR
课堂小结
Class summary
04
课堂小结
这节课你们都学会了哪些知识?
1、当两个一次函数的k一样,而b不一样,则这两个函数的图象是两条互相平行的直线,且它们之间可以通过平移得到(向上或向下),平移的距离是|b|。
2、当两个一次函数的b一样,而k不一样,则这两个函数的图象是两条相交的直线,且与y轴交于同一点,即(0,b)
Thank you!
人教版
八年级下册
第 19 章 一次函数
