人教版八年级下册20.2.1 方差 课件 (共27张PPT)
文档属性
| 名称 | 人教版八年级下册20.2.1 方差 课件 (共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-22 08:13:38 | ||
图片预览







文档简介
(共27张PPT)
课程:数学
《方差》
人教版
八年级下册 第4课时
第 20 章 数据的分析
教学目标
运用方差知识,解决实际问题,在解题过程中提高运用数学能力。
知识与技能
自主探究、实践解题,会用统计学的知识,分析解决问题。
过程与方法
进一步体会数学应用科学性。
情感态度和价值观
目
录
新课导入
New class introduction
探究新知
Explore new knowledge
课堂练习
class exercise
课堂小结
Class summary
01
02
03
04
新课导入
01
New class introduction
新课导入
1.何为一组数据的极差
极差反映了这组数据哪方面的特征
答: 一组数据中的最大值减去最小值所得的差叫
做这组数据的极差,极差反映的是这组数据
的变化范围或变化幅度.
2、样本9.9,10.3,10.3,9.9,10.1的极差是 .
3、一组数据3、-1、0、2、x的极差是5,
且x为自然数,则x= .
0.4
4或-2
探究新知
02
Explore new knowledge
探究新知
方差越大,说明数据的波动越大,越不稳定.
方差用来衡量一批数据的波动大小
(即这批数据偏离平均数的大小).
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
方差:各数据与它们的平均数的差的平方的平均数.
1、什么叫方差?公式?2、方差的作用是什么?
性质: (1)数据的方差都是非负数,即
(2)当且仅当每个数据都相等时,方差为零,反过来,若
探究新知
方差用来衡量一批数据的波动大小.(即这批数据偏离平均数的大小).
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
方差:各数据与它们的平均数的差的平方的平均数。
计算方差的步骤可概括为:
“先求平均数,再套用公式”.
3、计算方差的步骤是什么?
方差越大,数据波动越大;
方差越小,数据波动越小.
探究新知
探索发现
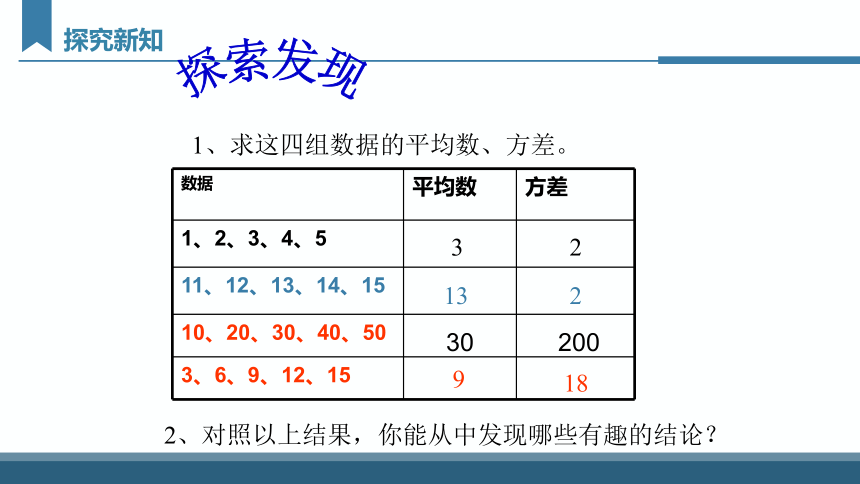
1、求这四组数据的平均数、方差。
2、对照以上结果,你能从中发现哪些有趣的结论?
数据 平均数 方差
1、2、3、4、5
11、12、13、14、15
10、20、30、40、50
3、6、9、12、15
3
2
13
2
9
18
30
200
探究新知
若数据x1、x2、…、xn平均数为 ,方差为S2,则
(3)数据ax1±b、ax2±b、…、axn±b
的平均数为 , 方差为a2S2
(1)数据x1±b、x2±b、…、xn±b
的平均数为 , 方差为S2
(2)数据ax1、ax2、…、axn的平均数为 ,
方差为a2S2
结论
探究新知
已知数据a1,a2,a3,…,an的平均数为x,方差为y, 则
①数据a1+3,a2 + 3,a3 +3 ,…,an +3的平均数为 ,
方差为 .
②数据a1-3,a2 -3,a3 -3 ,…,an -3的平均数为 ,
方差为 .
③数据3a1,3a2 ,3a3 ,…,3an的平均数为 ,
方差为 .
④数据2a1-3,2a2 -3,2a3 -3 ,…,2an -3的平均数为 ,方差为 -.
x+3
y
x-3
y
3x
9y
2x-3
4y
你能用所发现的结论来解决以下的问题:
探究新知
如果将一组数据中的每一个数据都加上同一个非零常数,那么这组数据的( )
A.平均数和方差都不变
B.平均数不变,方差改变
C.平均数改变,方差不变
D.平均数和方差都改变
C
探究新知
A
思考
探究新知
探究:1 甲、乙两小组各10名学生进行英语口语会话,各练习5次,他们每位同学的合格次数分别如下表:
(1) 哪组的平均成绩高?
(2) 哪组的成绩比较稳定?
探究新知
分析(1)比较平均成绩高低就是比较甲、乙
两组合格次数的平均数的大小.
(2)比较稳定程度应比较甲、乙两组
的方差或标准差.
所以甲、乙两组的平均成绩一样.
课堂练习
03
class exercise
课堂练习
1、在统计中,样本的方差和标准差可以近似的反映总体的( ).
A、平均状态
B、离散程度
C、分布规律
D、最大值和最小值
B
课堂练习
2、刘翔为了备战2008年奥运会,刻苦进行110米跨栏训练,为判断他的成绩是否稳定,教练对他10次训练的成绩进行统计分析,则教练需了解刘翔这10次成绩的( )
A、众数 B、方差
C、平均数 D、频数
B
课堂练习
3、在方差的计算公式 S2= [(x1-20)2+(x2-20)2+ +(x10-20)2]中,数字10和20分别表示( )
A、样本的容量和方差 B、平均数和样本的容量
C、样本的容量和平均数 D、样本的方差和平均数
10
1
C
课堂练习
4、对于数据3、2、1、0、-1
求:它的极差是————
方差是—————
标准差是—————
说说你是怎样思考,并口述求解过程?
4
2
课堂练习
(1)有5个数1,4,a, 5, 2的平均数是a,则这个
5个数的方差是_____.
(2)绝对值小于 所有整数的标准差是______.
(3)一组数据:a, a, a, ---,a (有n个a)则它的方差和标准差为___ ;
2
0
0
课堂练习
品种 各试验田每公顷产量 (单位:吨) 甲 7.65 7.50 7.62 7.59 7.65
7.64 7.50 7.40 7.41 7.41
乙 7.55 7.56 7.53 7.44 7.49
7.52 7.58 7.46 7.53 7.49
农科院对甲,乙两种甜玉米各用10块试验田进行
试验,得到两个品种每公顷产量的两种数据:
根据这些数据,应为农科院选择甜玉米种子提出怎样的建议?
课堂练习
说明在试验田中,甲,乙两种甜玉米的平均产量相差不大,由此估计在这个地区种植这两种甜玉米,它们的平均产量相差不大.
用计算器算得样本数据的平均数是:
X甲≈7.54 X乙≈7.52
用计算器算得样本数据的方差是:
S2甲≈0.01, S2乙≈0.002 得出 S2甲>S2乙
说明在试验田中,乙种甜玉米的产量比较稳定,进而可以推测要这个地区种植乙种甜玉米的产量比甲的稳定.
综合考虑甲乙两个品种的产量和产量的稳定性,可以推测这个地区更适合种植乙种甜玉米.
解:
课堂小结
04
Class summary
课堂小结
一、方差和标准差的计算公式
二、方差的简化计算公式
(数小时)
(数大时)
课堂小结
数理统计的基本思想:
用样本估计总体.
用样本的某些特性估计总体相应的特性.
用样本的平均数、中位数和众数去估计相应总体的平均水平特性.
用样本的方差去估计相应总体数据的波动情况.
Thank you!
第 20 章 数据的分析
课程:数学
《方差》
人教版
八年级下册 第4课时
第 20 章 数据的分析
教学目标
运用方差知识,解决实际问题,在解题过程中提高运用数学能力。
知识与技能
自主探究、实践解题,会用统计学的知识,分析解决问题。
过程与方法
进一步体会数学应用科学性。
情感态度和价值观
目
录
新课导入
New class introduction
探究新知
Explore new knowledge
课堂练习
class exercise
课堂小结
Class summary
01
02
03
04
新课导入
01
New class introduction
新课导入
1.何为一组数据的极差
极差反映了这组数据哪方面的特征
答: 一组数据中的最大值减去最小值所得的差叫
做这组数据的极差,极差反映的是这组数据
的变化范围或变化幅度.
2、样本9.9,10.3,10.3,9.9,10.1的极差是 .
3、一组数据3、-1、0、2、x的极差是5,
且x为自然数,则x= .
0.4
4或-2
探究新知
02
Explore new knowledge
探究新知
方差越大,说明数据的波动越大,越不稳定.
方差用来衡量一批数据的波动大小
(即这批数据偏离平均数的大小).
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
方差:各数据与它们的平均数的差的平方的平均数.
1、什么叫方差?公式?2、方差的作用是什么?
性质: (1)数据的方差都是非负数,即
(2)当且仅当每个数据都相等时,方差为零,反过来,若
探究新知
方差用来衡量一批数据的波动大小.(即这批数据偏离平均数的大小).
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
方差:各数据与它们的平均数的差的平方的平均数。
计算方差的步骤可概括为:
“先求平均数,再套用公式”.
3、计算方差的步骤是什么?
方差越大,数据波动越大;
方差越小,数据波动越小.
探究新知
探索发现
1、求这四组数据的平均数、方差。
2、对照以上结果,你能从中发现哪些有趣的结论?
数据 平均数 方差
1、2、3、4、5
11、12、13、14、15
10、20、30、40、50
3、6、9、12、15
3
2
13
2
9
18
30
200
探究新知
若数据x1、x2、…、xn平均数为 ,方差为S2,则
(3)数据ax1±b、ax2±b、…、axn±b
的平均数为 , 方差为a2S2
(1)数据x1±b、x2±b、…、xn±b
的平均数为 , 方差为S2
(2)数据ax1、ax2、…、axn的平均数为 ,
方差为a2S2
结论
探究新知
已知数据a1,a2,a3,…,an的平均数为x,方差为y, 则
①数据a1+3,a2 + 3,a3 +3 ,…,an +3的平均数为 ,
方差为 .
②数据a1-3,a2 -3,a3 -3 ,…,an -3的平均数为 ,
方差为 .
③数据3a1,3a2 ,3a3 ,…,3an的平均数为 ,
方差为 .
④数据2a1-3,2a2 -3,2a3 -3 ,…,2an -3的平均数为 ,方差为 -.
x+3
y
x-3
y
3x
9y
2x-3
4y
你能用所发现的结论来解决以下的问题:
探究新知
如果将一组数据中的每一个数据都加上同一个非零常数,那么这组数据的( )
A.平均数和方差都不变
B.平均数不变,方差改变
C.平均数改变,方差不变
D.平均数和方差都改变
C
探究新知
A
思考
探究新知
探究:1 甲、乙两小组各10名学生进行英语口语会话,各练习5次,他们每位同学的合格次数分别如下表:
(1) 哪组的平均成绩高?
(2) 哪组的成绩比较稳定?
探究新知
分析(1)比较平均成绩高低就是比较甲、乙
两组合格次数的平均数的大小.
(2)比较稳定程度应比较甲、乙两组
的方差或标准差.
所以甲、乙两组的平均成绩一样.
课堂练习
03
class exercise
课堂练习
1、在统计中,样本的方差和标准差可以近似的反映总体的( ).
A、平均状态
B、离散程度
C、分布规律
D、最大值和最小值
B
课堂练习
2、刘翔为了备战2008年奥运会,刻苦进行110米跨栏训练,为判断他的成绩是否稳定,教练对他10次训练的成绩进行统计分析,则教练需了解刘翔这10次成绩的( )
A、众数 B、方差
C、平均数 D、频数
B
课堂练习
3、在方差的计算公式 S2= [(x1-20)2+(x2-20)2+ +(x10-20)2]中,数字10和20分别表示( )
A、样本的容量和方差 B、平均数和样本的容量
C、样本的容量和平均数 D、样本的方差和平均数
10
1
C
课堂练习
4、对于数据3、2、1、0、-1
求:它的极差是————
方差是—————
标准差是—————
说说你是怎样思考,并口述求解过程?
4
2
课堂练习
(1)有5个数1,4,a, 5, 2的平均数是a,则这个
5个数的方差是_____.
(2)绝对值小于 所有整数的标准差是______.
(3)一组数据:a, a, a, ---,a (有n个a)则它的方差和标准差为___ ;
2
0
0
课堂练习
品种 各试验田每公顷产量 (单位:吨) 甲 7.65 7.50 7.62 7.59 7.65
7.64 7.50 7.40 7.41 7.41
乙 7.55 7.56 7.53 7.44 7.49
7.52 7.58 7.46 7.53 7.49
农科院对甲,乙两种甜玉米各用10块试验田进行
试验,得到两个品种每公顷产量的两种数据:
根据这些数据,应为农科院选择甜玉米种子提出怎样的建议?
课堂练习
说明在试验田中,甲,乙两种甜玉米的平均产量相差不大,由此估计在这个地区种植这两种甜玉米,它们的平均产量相差不大.
用计算器算得样本数据的平均数是:
X甲≈7.54 X乙≈7.52
用计算器算得样本数据的方差是:
S2甲≈0.01, S2乙≈0.002 得出 S2甲>S2乙
说明在试验田中,乙种甜玉米的产量比较稳定,进而可以推测要这个地区种植乙种甜玉米的产量比甲的稳定.
综合考虑甲乙两个品种的产量和产量的稳定性,可以推测这个地区更适合种植乙种甜玉米.
解:
课堂小结
04
Class summary
课堂小结
一、方差和标准差的计算公式
二、方差的简化计算公式
(数小时)
(数大时)
课堂小结
数理统计的基本思想:
用样本估计总体.
用样本的某些特性估计总体相应的特性.
用样本的平均数、中位数和众数去估计相应总体的平均水平特性.
用样本的方差去估计相应总体数据的波动情况.
Thank you!
第 20 章 数据的分析
